Observations on Irreducible Sets and Sober Spaces

CHEN Dong-li,ZHANG Yan

(1.School of Science,Xi’an University of Architecture and Technology,Xi’an 710055,China; 2.Huaqing College,Xi’an University of Architecture and Technology,Xi’an 710043,China)

Observations on Irreducible Sets and Sober Spaces

CHEN Dong-li1,ZHANG Yan2

(1.School of Science,Xi’an University of Architecture and Technology,Xi’an 710055,China; 2.Huaqing College,Xi’an University of Architecture and Technology,Xi’an 710043,China)

This paper,using the monads theory in the topological space,gives a new characterization of irreducible sets in the nonstandard enlarged models.Further,the discretization expression of Sober topological spaces is presented.

monad;irreducible set;Sober space;discretization

§1.Introduction

The monad of a point(set)in topological spaces is a very important concept,which can be used for researching the properties of topological spaces by nonstandard analysis,especially separation[1].It is a generalization of“inf i nitesimal”in general topological spaces[2]and is applicable for discretization expression for many topological properties.For example,the topological space(X,τ)is a T2-sapce(Hausdorf f)if ffor any x,y∈X,if x/=y,then m(x)∩m(y)/=∅,where m(x)is the monad of x.Sober property between T0and T2but independent of T1is a special separation and has important applications in continuous spectrum[3].

In this paper,using monads theory,we will give the expressions of irreducible set and Sober space in the nonstandard enlarged models.Throughout this paper we suppose that the topological space X is the subset of individuals S of the standard universe U[4]and thus X⊂∗X.

Def i nition 1.1[5]Assume that∗U is a nonstandard model of U.∗U is called the nonstandard enlarged model of U if for any collection{Ai|i∈I}with f i nite intersection property such that

Remark 1.1Collection{Ai|i∈I}has the f i nite intersection property if ffor any f i nite subfamily

Def i nition 1.2[5]Assume that(X,τ)is a topological space and τxis the open neighborhood systems of x∈τ.Then m(x)=G is called the monad of x.

Remark 1.2y∈X is called a near standard point in∗X if there exists a x∈X such that y∈m(x).Denote st(y)={x∈X:y∈m(x)}and y≈x for y∈m(x)[6].

Lemma 1.1Assume that A⊂X and A stands for the closure of A.Then

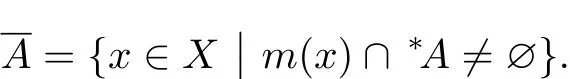
ProofIf x∈A,then G∩A/=∅,G∈τx.Then{G∩A|G∈τx}has the property of fi nite intersection.Due to this result,

On the other hand,if m(x)∩∗A/=∅,then∗G∩∗A/=∅,G∈τx.Using the transfer principle[7],G∩A/=∅and thus x∈A.

From Lemma 1.1,it is not difficult to obtain that if A⊂X,then st(∗A)=A.

De fi nition 1.3[8]Assume that(X,τ)is a topological space and A⊂X is a nonempty closed set.A is called the irreducible closed set if A=F1∪F2implies that A=F1or A=F2, where F1and F2are closed sets.

Obviously,for each x∈X,{x}−is the irreducible closed set,where“−”represents the closure operator.

De fi nition 1.4The topological space(X,τ)is called a Sober space if each irreducible closed set A has the form of{x}−,where x∈X.

§2.Main Results

In this section,we give new characterizations of irreducible set and Sober space by monads theory.

Lemma 2.1Let A be a closed subset of topological space(X,τ).Then A={x}−if f x∈A and m(x)⊆m(y)for all y∈A.

Proof(Necessity)A={x}−implies x∈A.Using Lemma 1.1,for each y,we have that x∈m(y)and thus m(x)⊂m(y).

(Sufficiency)By the given conditions,x∈m(y)for all y∈A.Again by Lemma 1.1, y∈{x}−.Since A is closed and x∈A,A={x}−.

Lemma 2.2[5](X,τ)is a T0-space if fx=y is equivalent to m(x)=m(y)for any x,y∈X.

Theorem 2.1Let the conditions in Lemma 2.1 hold.A is irreducible if f∅.

Proof(Necessity)Suppose that A is a irreducible closed set.Choose x,y∈A,G1∈τx,G2∈τy.If A∩G1∩G2=∅,then A=(A−G1)∪(A−G2).The irreducibility of A implies that

Then,A∩G1=∅or A∩G2=∅.This leads to a contradiction.Therefore,

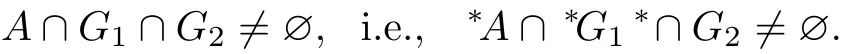
Since G1and G2are arbitrary,∗A∩m(x)∩m(y)/=∅.Consequently,

(Sufficiency)Suppose,by contradiction,that A is reducible.By the def i nition of the irreducible set,there exist closed sets F1,F2such that

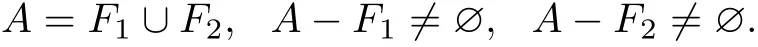
Choose x∈A−F1and y∈A−F2.By the given conditions,there is α∈∗A such that α∈µ(x)∩µ(y).Then,α∈∗X−∗F1and α∈∗X−∗F2.Thus,we obtain that α∈(∗X−F1)∩(∗X−F2)=∗X−∗(F1∪F2)=∗X−∗A,a contradiction.

Using Theorem 2.1,we now give a nonstandard expression of Sober space.

Theorem 2.2Let(X,τ)be a topological space.X is a Sober space if ffor any closed set

Proof(Necessity)Let A be a closed subset of X such thatTheorem 2.1,A is a irreducible closed set.Thus,there exists x∈X such that A={x}−. Lemma 2.1 yields that m(x)⊂m(y),y∈A.Hence(Sufficiency)Assume that A⊂X is a irreducible closed set.Let.Then x∈A and m(x)⊆m(y)for y∈A.From Lemma 2.1,we have A={x}−.

Corollary 2.1If(X,τ)is a Hausdor ffspace,then it is a Sober space.

ProofLet A⊂X be a irreducible closed set.If there exist x,y∈A and x/=y,then m(x)∩m(y)=∅since X is Hausdor ff.This contradicts with Theorem 2.1.Therefore,there must be x∈X such that A={x}={x}−and thus(X,τ)is a Sober space.

Corollary 2.2If(X,τ)is a Sober space,then it is a T0-space.

ProofLet x,y∈X and m(x)=m(y).It suffices to show x=y.Let A={x,y}.Since m(x)=m(y),A∩m(x)∩m(y)/=∅.By Theorem 2.1,A={x,y}−is irreducible.Further,the fact that X is a Sober space implies x=y.It follows from Lemma 2.2 that(X,τ)is T0.

[1]FESENKO I.Several nonstandard remarks[J].American Mathematical Society Translations,2006,217(2): 37-50.

[2]KOSSAK R.What are inf i nitesimals and why they cannot be seen[J].The American Mathematical Monthly, 1996,103(10):846-853.

[3]ZHANG Shi-fang,WU Zhen-ying,ZHONG Huai-jie.Continuous spectrum,point spectrum and residual spectrum of operator matrices[J].Linear Algebra and Its Applications,2010,433(3):653-661.

[4]ROBINSON A.Nonstandard Analysis[M].Amsterdam:North-Holland,1966.

[5]LUXEMBURG W A J.A General Theory of Monads[M].New York:Halt,1969.

[6]CHEN Dong-li,MA Chun-hui,SHI Yan-wei.The quai-near-standard points in a metric space and the nonstandard completion of metric space[J].Journal of Shaanxi Normal University,2008,36(3):10-12.

[7]DAVIS M.Applied Nonstandard Analysis[M].New York:Wiley,1977.

[8]KELLEY J L.General Topology[M].New York:Springer-Verlag,1955.

tion:03H05

1002–0462(2014)04–0501–04

date:2012-11-26

Supported by the Natural Science Foundation of Shaanxi Province(2007A12);Supported by the Scientif i c Research Foundation of Shaanxi Educational Committee(11JK0507)

Biography:CHEN Dong-li(1963-),male,Xi’an,Shaanxi,a professor of Xi’an University of Architecture and Technology,M.S.D.,engages in nonstandard analysis.

CLC number:O141.41Document code:A