给定悬挂点数图的Wiener指数的极图
2014-07-19余桂东邢抱花
段 兰,余桂东,邢抱花
(安庆师范学院数学与计算科学学院,安徽安庆 246133)
给定悬挂点数图的Wiener指数的极图
段 兰,余桂东,邢抱花
(安庆师范学院数学与计算科学学院,安徽安庆 246133)
设G是一个简单图,图G的Wiener指数是G中所有顶点的距离之和。本文刻画了给定顶点数和悬挂点数的图类中,W iener指数取到最小、次小、第三小的极图,并由此确定了关于悬挂点数的Wiener指数的下界。
图;Wiener指数;悬挂点
设G(V(G),E(G))是一个简单无向图,V(G)为图G的顶点集,E(G)为图G的边集。G中两个顶点u,v之间的距离定义为G中连接u和v最短路的长度,记为dG(u,v)。图G中任意两点距离的最大值称为G的直径。图G的Wiener指数,记作W(G),定义为图G的所有点对的距离之和,即

Wiener指数广泛应用于描述分子结构,它是于1947年由Harold Wiener作为路径数目来引入的。Wiener根据化学中碳原子之间路径距离的计数,提出了这个刻划分子结构的指数,该指数等于碳氢化合物中所有最短碳-碳键路径之和。有关Wiener指数的结构性质可参阅[1]。
若用xi表示图G中距离为i的顶点对个数,d为图G的直径,则Wiener指数也可表示为:
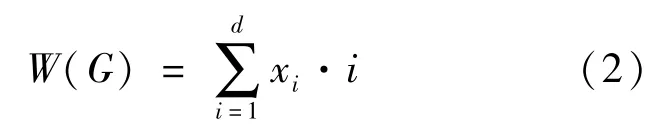
若图G的直径较小,则用(2)式来计算图的Wiener指数较为方便[2]。但对于任意一个图,若其直径较大,我们很难给出每一个xi的确切值,因此对于某类图,给出其Wiener指数的上界或下界是非常有意义的[3-4]。设M是具有n个顶点且悬挂点数为q的图类,本文将给出图类M中,Wiener指数取到最小、次小、第三小的唯一的图,并由此确定了Wiener指数关于悬挂点的下界。
本文所获主要结论如下。
设M是具有n个顶点,且悬挂点数为q的图类。设B(n,q)是完全图Kn-q上的顶点v1附着q个悬挂点的图,B1(n,q)是完全图Kn-q上顶点v1附着q个悬挂点且在Kn-q上删去不与v1连接的一条边的图,B2(n,q)是完全图Kn-q上顶点v1附着q-1个悬挂点且在另一顶点v2附上一个悬挂点的图,或是完全图Kn-q上在顶点v1附着q个悬挂点且在Kn-q上删去均不与v1相连的两条边的图,Bv1v2(n,q)是B(n,q)中删去完全图Kn-q中与顶点v1相连的一条边v1v2所形成的图是删去中完全图Kn-2的一条边且该边与顶点v1和v2都不相连的边v3v4所得的图。
引理1设图G(V(G),E(G))是一个简单无向图,若边uv∉E(G),而点u,v∈V(G),图G +uv表示图G中添上不相邻的边uv所构成的图,则W(G)>W(G+uv);若边uv∈E(G),点u,v∈V(G),图G-uv表示图G中删除边uv所构成的图,则W(G)<W(G-uv)。
证明若图G中边uv∉E(G),而点u,v∈V(G),则dG(u,v)>1,而dG+uv(u,v)=1,所以dG(u,v)>dG+uv(u,v)。而对于∀u′,v′∈V(G),且{u,v}≠{u′,v′}时,都有dG(u′,v′)≥dG+uv(u′,v′),故由Wiener指数的定义知W(G)>W(G+uv)。
同理可证,当边uv∈E(G),点u,v∈V(G)时,W(G)<W(G-uv)。
定理2B(n,q)是M中Wiener指数取到最小的唯一的图,且∀G∈M有

当且仅当G=B(n,q)时取等号。
证明设G1是图类M中是由一个顶点数为n-q的图G上系q个悬挂点所构成的图,G2是完全图Kn-q上系q个悬挂点的图。若图G不是完全图Kn-q,由引理1知W(G1)>W(G2)。
假设G2≠B(n,q),不妨设G2为完全图Kn-q的i顶点v1,v2,…,vi(1≤i≤n-q)上分别系q1,q2,…,qi个悬挂点所构成的图,且q=q1+q2+…+qi,则

故B(n,q)为图类M中Wiener指数取到最小的唯一图。

当且仅当G=B(n,q)时取等号。
定理3若q≤n-3(n≥4),则图类M中Wiener指数取到次小的唯一图:当q≠2时,为B1(n,q);当q=2时,为B1(n,2)和B2(n,2),且当q≠2时,当且仅当G=B1(n,q)时取等号;当q=2时,当且仅当G=B1(n,2)或B2(n,2)时取等号。
证明由定理2知,B(n,q)是图类M中W iener指数取到最小的唯一的图。由引理1与图类M的定义知,有两种方法可以得到M中Wiener指数取到次小的图:一是删去B(n,q)中完全图Kn-q中的一条边(此q≥1时);二是将B(n,q)中v1上的一个悬挂点移到其他顶点(如v2)上,此时要求q≥2。
方法1当q≥1时,删去B(n,q)中完全图Kn-q中的一条边,得到的图为B1(n,q)或Bv1v2(n,q)。

方法2当q≥2时,B(n,q)将中顶点v1上的一个悬挂点移到其他顶点(如v2)上所得的图B2(n,q)。

当q=2时,W(B1(n,q))=W(B2(n,q)),即W(B1(n,2))=W(B2(n,2))。
当q>2时,W(B1(n,q))<W(B2(n,q))。
综上所述,当q≠2时,图类M中Wiener指数取到次小的唯一图为B1(n,q);当q=2时,图类M中Wiener指数取到次小的图为B1(n,2)或B2(n,2),且只有这两个图为次小图。

定理4若q≤n-5(n≥6),则图类M中Wiener指数取到第三小的图:当q=1时,为Bv1v2(n,1),Bv4v51(n,1)和Bv3v41(n,1);当q=2时,

证明由引理1、定理2、定理3及图类M的定义知,图类M中W iener指数取到第三小的图可能在这三种图中产生:一是B2(n,q)(q≥2);二是Bv1v2(n,q);三是在B1(n,q)上进行删非悬挂边或移悬挂点(移悬挂点时要求q≥2)所得的图,且当q=2时,再加上第四种可能性,即在B2(n,2)上进行删非悬挂边所得的图。
不妨设B1(n,q)是完全图Kn-q中顶点v1上悬着q个悬挂点,在Kn-q上删去不与v1连接的一条边v2v3,且有非悬挂v4,v5点的图。在图B1(n,q)的基础上进行删非悬挂边或移悬挂点有六种方法:一是删去边v1v2所得的图,记为Bv1v21(n,q);二是删去边v1v4所得的图,记为Bv1v41(n,q);三是删去边v4v5所得的图,记为Bv4v51(n,q);四是删去边v3v4所得的图,记为Bv3v41(n,q);五是将顶点v1上的1个悬挂点,移到顶点v2上所得的图,记为六是将顶点v上的一个悬挂
1点,移到顶点v4上所得的图,记为Bv41(n,q)(q≥2)。
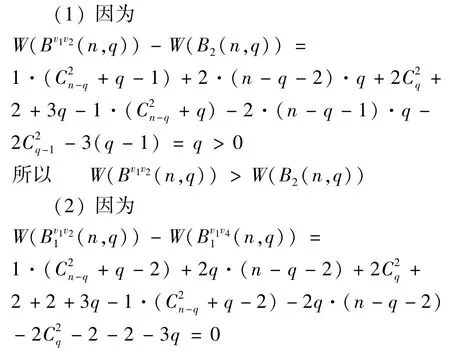

(9)当q=2时,再加上第四种可能性,即在B2(n,2)上进行删非悬挂边所得的图。不妨设B2(n,2)是完全图Kn-p中顶点v1,v2上分别悬了1个悬挂点,且包含非悬挂点v3,v4的图。由引理1知在B2(n,2)上有三种删非悬挂边的方法:一是删去边v1v3所得的图,记为Bv1v32(n,2);二是删去边v3v4所得的图,记为Bv3v42(n,2);三是删去边v1v2所得的图,记为Bv2v32(n,2)。


[1]H.Wiener.Structural determination of paraffin boiling points[J].J.Amer.Chem.Soc.,1947,69:17-20.
[2]汤自凯,郑汉元.单圈图的Wiener指数[D].湖南师范大学,2007.
[3]汤自凯,郑汉元.一类双圈图中具有最大、最小Wiener指数的图[J].湖南师范大学自然科学学报,2008,31:27-30.
[4]万花,任海珍.一类三圈图的Wiener指数[J].数学研究,2012,45(2):207-212.
[5]I.Gutman,J.H.Potgieter.Wiener index and intermolecular forces[J].J.Serb.Chem.Soc.,1997,62:185-192.
[6]Dobrym in a Gutm,S.Klavzar,et al.Wiener index of hexagonal system s[J].Acta App.Math.,2002,72:247-294.
[7]B.Zhou,X.Cai,N.Trinajstic.On reciprocal complementary Wiener number of trees[J].Discrete Appl.Math.,2009,157:1628-1633.
[8]S.Nikolic,C.J.Trina.The Wiener index:developments and applications[J].Groat.Chem.Acta.,1995,68:105-129.
[9]X.Qi,B.Zhou.Extremal properties of reciprocal complementary Wiener number of trees[J].Computers and Mathematics with Applications,2011,62:523-531.
[10]H.Liu,M.Lu.A unified approach to extremal cacti for different indices[J].MATCH Commun.Math.Comput.Chem.,2007,58:193-204.
ExtremalGraph of theWiener Index of Graphswith Given Number of Suspension Points
DUAN Lan,YU Gui-dong,XIN Bao-hua
(School of Mathematics and Computational Sciences,Anqing Teachers College,Anqing 246133,China)
Let be a simple graph,theWiener index of is the sum of distances between all pairs of vertices of.In this paper,we characterize the extremal graph with the first,the second and the third smallestWiener index among all graphswith given order and the number of suspension points,and give the lower bounds of the Wiener index of graphs with given number of suspension point.
graph,Wiener index,suspension point
O157.5
A
1007-4260(2014)03-0028-04
时间:2014-9-15 16:07 网络出版地址:http://www.cnki.net/kcms/doi/10.13757/j.cnki.cn34-1150/n.2014.03.008.html
2014-02-26
安徽省自然科学基金(11040606M14),安徽省高校自然科学重点项目基金(KJ2011A195,KJ2013A196)和安庆师范学院青年科学研究基金(KJ201307)资助。
段兰,女,安徽太湖人,安庆师范学院数学与计算科学学院硕士研究生,研究方向为图论及其应用。
