一种结构化LDPC码的部分并行译码器设计

苏悦 王建辉

(1 湖南北云科技有限公司, 长沙 410073)(2 国防科技大学, 长沙 410073)

一种结构化LDPC码的部分并行译码器设计

苏悦1王建辉2

(1 湖南北云科技有限公司, 长沙 410073)(2 国防科技大学, 长沙 410073)

CCSDS标准给出的低密度奇偶校验码(Low Density Parity Check，LDPC)其子矩阵具有不同的列重，这给部分并行译码器的设计带来困难。本文针对如何高效实现CCSDS中LDPC码部分并行译码的问题，根据该类码的准循环特性，将码的校验矩阵分解成3个矩阵的和，提出了一种能够部分并行译码的译码器结构。利用本文提出的方法设计译码器时可以在译码时延和译码复杂度之间进行折中。

CCSDS标准；LDPC码；部分并行译码器

1 引言

低密度奇偶校验码(Low Density Parity Check，LDPC)由Gallager于1962年提出[1]，但受限于当时的技术条件并没有引起人们的重视。直到1996年，Mackay等人重新发现LDPC码的优异性能[2]，该类码才受到研究人员的关注，并得到越来越广泛的应用。LDPC码按校验矩阵的构造方法可分为随机构造的LDPC码和结构化LDPC码。比特填充(Bit-filling)[3]算法和PEG算法[4]均为随机LDPC码构造方法。随机LDPC码一般而言性能优异，但编译码复杂度较大。结构化LDPC码构造法包括有限几何构造法[4-5]、基于循环置换矩阵的构造法[6]、原模图法[7]等，设计优良的结构化LDPC码不但性能优异，而且编译码复杂度低，实用性强。近年来，LDPC码得到了广泛的应用，空间数据系统咨询委员会(CCSDS)已经将一类LDPC码，即四次重复锯齿累积 (Accumulate Repeat-4 Jagged Accumulate，AR4JA)码[8-9]推荐为深空通信和近地通信的标准。该类码具有准循环结构，编译码器设计比随机构造的码简单。但该类码具有多种不同列重的子矩阵，不利于译码器的工程实现。

本文提出了一种针对CCSDS推荐的用于深空通信的1/2码率LDPC码的译码器结构，该译码器能够实现并行度较高的部分并行译码，便于工程实现时在译码时延和实现复杂度之间折中。本文提出的译码器结构可为译码器的工程实现提供更大的灵活性。

2 AR4JA码

LDPC码为线性分组码，可以由校验矩阵表示。1981年，Tanner就已经提出线性分组码的图模型表示法[10]，描述了码字比特与约束它们的校验和之间的对应关系，奠定了LDPC码和其他基于图的码的研究基础。式(1)和图1分别为一个LDPC码的校验矩阵及其Tanner图表示方法。Tanner图中圆形与方形分别与校验矩阵的列和行一一对应，分别称为变量接点和校验节点。Tanner图为二分图，其顶点集可以划分成两个子集VS和VC，使得每条边的一个端点在VS中，另一个端点在VC中，子集VS与VC中各自内部的节点互不相连。假设子集VS中的节点对应码字比特的n个变量节点(圆形)集合(s1,s1…sn)，子集VC中的节点对应校验约束关系中的m个校验节点(方形)集合(c1,c2,…cm)，当且仅当第u个码字比特参与了第v个奇偶校验约束时，变量节点su和校验节点cv之间才有一条边(su,cv)相连，即Tanner图中对应的节点之间建立一条边。在Tanner图中定义一个节点度数为与此节点相连的边的数量。因此，变量节点的度数等于包含该变量节点的校验约束关系的个数或H矩阵中对应行的重量；校验节点的度数等于被该校验约束关系控制的变量节点的个数或H矩阵中对应列的重量。

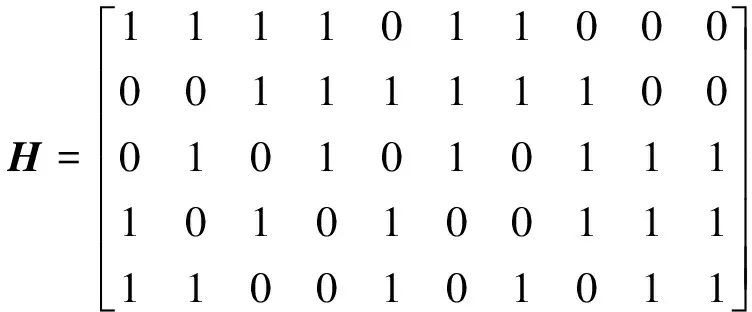
(1)

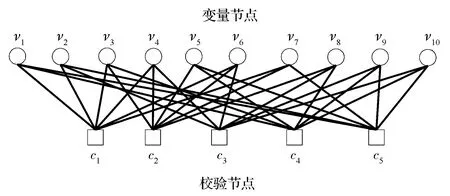
图1 LDPC码的Tanner图表示

AR4JA码为CCSDS中推荐用于深空和近地通信的LDPC码，该类码具有准循环结构，但其部分子矩阵中每一列包含‘1’的数量较多，这给部分并行译码器的设计带来了困难，本文主要针对该问题展开研究。AR4JA 码的校验矩阵如式(2)所示，完成编码后与校验矩阵最后M列对应的校验位被打孔，该码的码率为1/2。

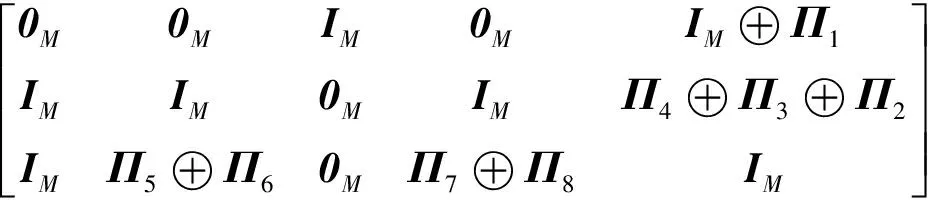
(2)

式中：每个分块矩阵均为M×M的矩阵。0M表示全零矩阵；IM表示单位矩阵。Πw(1≤w≤8)表示单位矩阵的置换矩阵，该矩阵只有在第x行第πk(x)列不为零，其他位置全为零。πk(x)的表达式为

(3)

式中：θw和φw(·)为CCSDS标准中给出的确定分块矩阵相对于单位矩阵的循环右移值的两个参数，其值可通过查表得到，当M的值为512时，θw和φw(·)的值如表1所示。

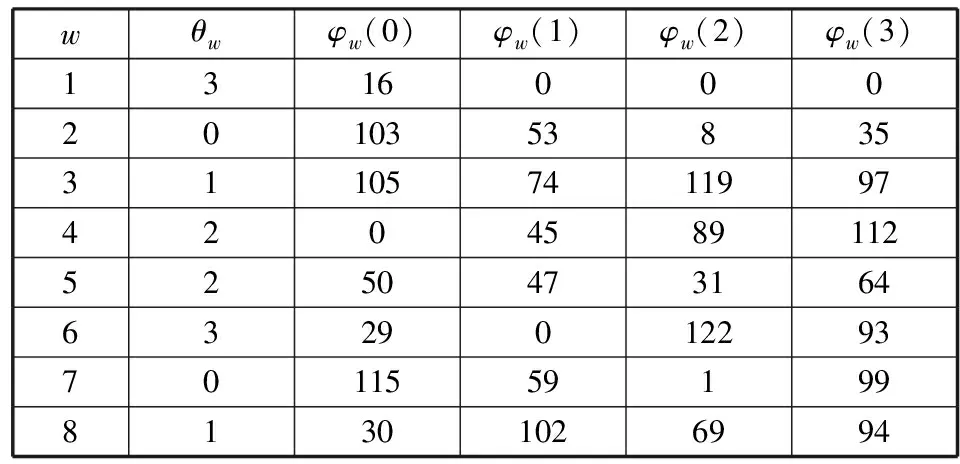
表1 AR4JA LDPC码参数表

3 CCSDS中1/2码率LDPC码的编码器

编码之前的信息位矢量记为[s1s2]，s1和s2分别为信息位的前M位和后M位。记与校验矩阵的后三列子矩阵对应的校验位矢量分别为p1、p2和p3，由码字和校验矩阵的关系可得

(4)

由上式可得三个校验位矢量的表达式为

(5)

(6)

(7)

由上述表达式可求得校验位，完成编码后校验位矢量p3被打孔。

4 AR4JA码的部分并行译码器设计

4.1校验矩阵的拆分

CCSDS中的AR4JA码的校验矩阵由三行五列维数为M×M的子矩阵组成，若每个非零子矩阵的每行、每列均只包含一个‘1’，则将校验节点和变量节点存储器按子矩阵的行和列进行适当划分后，可以实行同时对M个变量节点或校验节点的更新。将AR4JA码的校验矩阵拆分为3个矩阵的和后，可确保每个非零子矩阵的每行、每列均只包含一个‘1’。拆分后的矩阵如下式所示，每个矩阵均由M×M的子矩阵构成，且每个非零子矩阵的每行、每列均只包含一个‘1’。设计译码器时，分别按照3个矩阵读入校验节点或变量节点软信息可实现部分并行译码。

(8)

(9)

(10)

4.2部分并行译码器结构

本文译码算法采用传统的归一化最小和算法，译码器工作时逐个更新校验节点和变量节点，每次译码的最大迭代次数为100次。

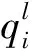
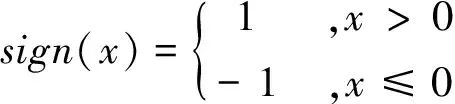
最小和算法的计算步骤如下：

1)初始化

(11)

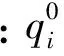
(12)

2)校验节点更新

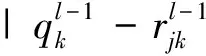
(13)

式中：λ为归一化系数。

3)变量节点更新

(14)

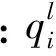
4)l次迭代后进行检测

若输出结果满足校验矩阵，则输出信息位

(15)

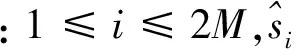
将校验矩阵拆分为3个矩阵的和后，分别按照3个矩阵的结构读取变量节点和校验节点软信息可以实现部分并行译码，但读完整个校验矩阵需要3次读取过程。若同时更新的节点数量为M1变量节点与校验节点软信息存储结构如下：与同一个子矩阵的第i个M1列对应的变量节点软信息分别存储在M1个不同的存储器中，与同一个子矩阵的第i个M1行对应的校验节点软信息分别存储在M1个不同的存储器中。为了便于实现，设M1为M的因子，M的值为512时，M1可取的值为：20、21、22、23、24、25、26、27、28、29。可根据对译码时延的要求选择译码器部分并行的倍数。每个变量节点软信息存储器的大小为5M/M1，每个校验节点软信息存储器的大小为3M/M1。变量节点和校验节点软信息存储器的数量均为M1个。部分并行译码器的结构如图2所示。

采用本文提出的校验矩阵拆分方法将CCSDS中的AR4JA码校验矩阵分解为3个矩阵的和后，每个分解后的矩阵中包含的非零子矩阵的列重均为1。采用常规准循环译码器的软信息存储结构，分别按照分解后的3个矩阵读取信息时，不会存在寄存器的访问冲突，可以实现部分并行读写操作。

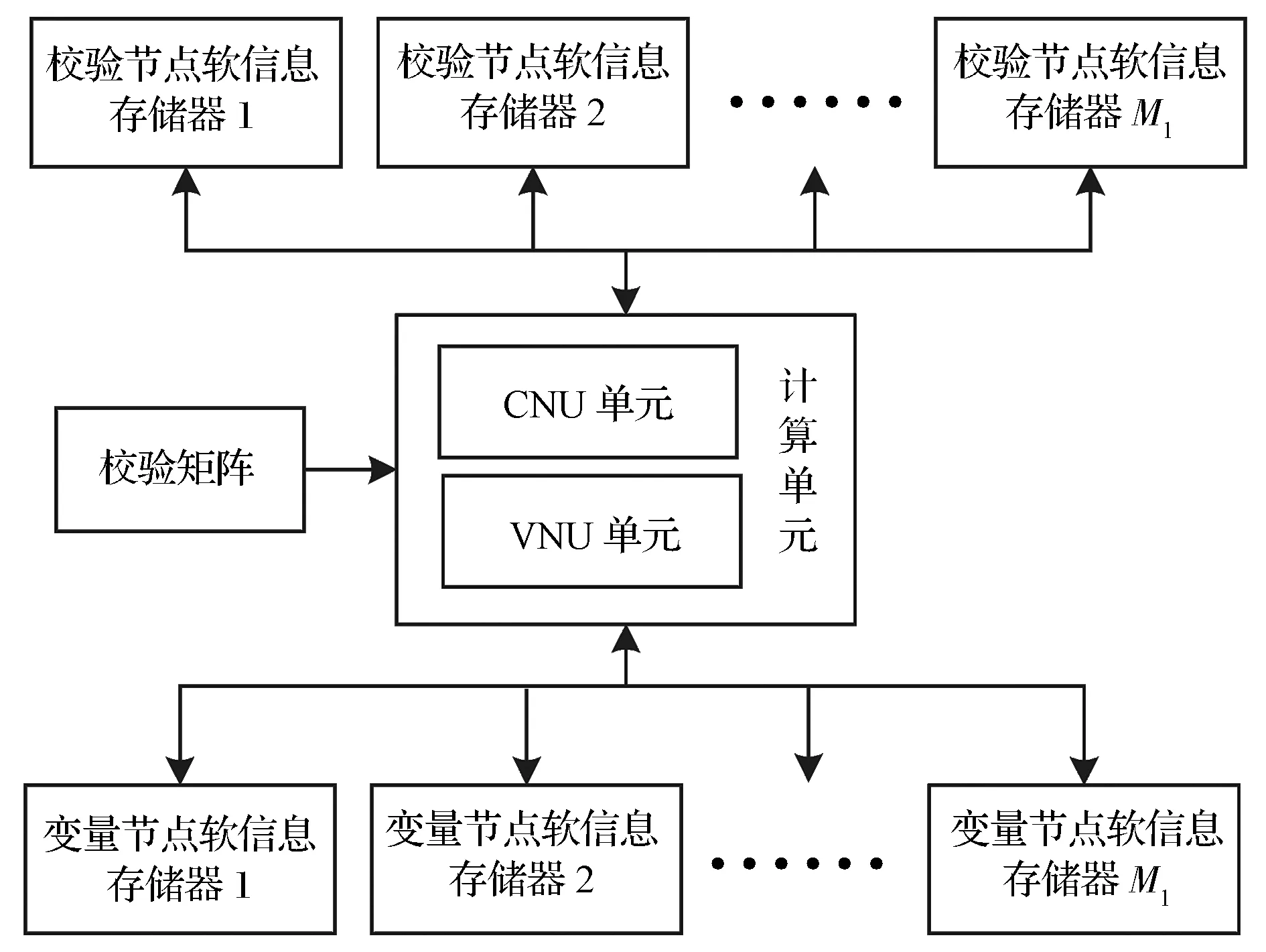
图2 部分并行译码器结构图

5 结束语

CCSDS推荐的LDPC码适用于卫星通信等领域，该码具有准循环结构，其校验矩阵由循环矩阵阵列构成，这为译码器的设计提供了更大的灵活性。但CCSDS标准中给出的LDPC码校验矩阵中，非零子矩阵的列重不同，这为部分并行译码器的设计带来困难，若直接套用常规的部分并行译码器结构，将使得列重不为1的子矩阵对应的软信息不能同时更新。本文通过矩阵拆分实现部分并行译码的方法，解决了分块矩阵列重不同时部分并行译码器难以实现的问题。

References)

[1]R G Gallager. Low-density parity-check codes[M]. Cambridge, MA: MIT Press, 1963

[2]D J C Mackay, R M Neal. Near Shannon-limit performance of low-density parity-check codes[J]. Electron. Lett., 1996, 32(16): 1645-1646

[3]J Campello, D S Modha, S Rajagopalan. Designing LDPC codes using bit-filling[C]// IEEE International Conference on Communications. New York: IEEE, 2001:55-59

[4]Shu Lin, Daniel J, Costello Jr. Error control coding[M]. Upper Saddle River, New Jersey: Prentice Hall, 2004

[5]Kou Yu, S Lin, M P C Fossorier. Low-density parity-check codes based on finite geometries: a rediscovery and new results[J]. IEEE Trans. Inf. Theory, 2001, 47(7): 2711-2736

[6]M Fossorier. Quasi-cyclic low-density parity-check codes from circulant permutation matrices[J]. IEEE Trans. Inf. Theory, 2004, 50(8): 1788-1793

[7]Jeremy Thorpe. Low density parity check (LDPC) codes constructed from protographs[R]. Pasadena: JPL, 2003

[8]Andrews K, Divsalar D, Dolinar S. The development of turbo and LDPC codes for deep space applications[J]. IEEE special Issue on Technical Advances in Deep Space Communication and Tracking, 2007: 2142-2156

[9]Andrews K, Divsalar D, Dolinar S. Design and standardization of low-density parity-check codes for space applications[C]// SpaceOps 2008 Conference. Heidelberg: American Institute of Aeronautics and Astronautics, 2008: 1-12

[10]R M Tanner. A recursive approach to low complexity codes[J]. IEEE Trans. Inform. Theory, 1981, 27(9):533-547

(编辑：张小琳)

A Partially Parallel Decoder Design of Structured LDPC Codes

SU Yue1WANG Jianhui2

(1 Hunan Beiyun Technology Co. Ltd., Changsha 410073, China)

(2 National University of Defense Technology, Changsha 410073, China)

Some LDPC codes with different rates for deep space communication are provided in CCSDS standard. These codes have quasi-cyclic structure, and can afford high coding gain and implementation flexibility of encoder and decoder for satellite crosslink system of COMPASS. But the column weight of sub-matrices of the code are different, which makes the implementation of parallel decoder of the code difficult. Based on the quasi-cyclic characteristic, the parity check matrix of each code is decomposed into three-matrice sum, and a decoder structure which can be implemented in a partially parallel way is presented in this paper. Tradeoff can be made between decoding delay and implementation complexity with the presented method.

CCSDS standard; LDPC code; partially parallel decoder

2014-03-25；

：2014-05-07

苏悦，女，硕士，工程师，从事北斗导航设备整机研发与软件研制。Email：suyue@beiyun.cc。

TN911.22

：ADOI：10.3969/j.issn.1673-8748.2014.03.014