移动式救援机器人的动力学仿真分析

张学军，张欣,，丛佩超

(1.东北电力大学 机械工程学院，吉林 132021；2.辽宁工程技术大学 机械工程学院，辽宁 阜新 123000)

移动式救援机器人的动力学仿真分析

张学军1，张欣1,2，丛佩超2

(1.东北电力大学 机械工程学院，吉林 132021；2.辽宁工程技术大学 机械工程学院，辽宁 阜新 123000)

利用雅克比矩阵概念与拉格朗日乘子方程，分别建立了移动式救援机器人系统的运动学与动力学模型，并以系统的动力学模型为基础，研究了移动式救援机器人的动力学分析过程。为实现对移动式救援机器人工作端轨迹的跟踪控制，提出了一种基于工作空间的逆动力学控制算法。利用Matlab软件，对所得到的运动学、动力学模型与逆动力学控制算法进行了仿真验证。

移动式救援机器人；工作端轨迹；仿真分析；逆动力学控制

0 引言

在人类赖以生存的自然环境中，各种自然灾害和人为事故如：水灾、火灾、雪灾、地震、核泄漏、恐怖袭击等，层出不穷，严重地危害着人类的生命安全。面对以上这些自然灾害和人为事故时，传统的救援方法通常是派遣救援人员到灾害或事故现场进行救援，这种方法使救援人员处于非常危险的境地。随着机器人技术的不断发展，利用救援机器人来替代人类完成救援工作成为可能[1-4]。

移动式救援机器人系统的机械手臂在救援过程中，扮演着重要的角色。当机械臂需要对不同的目标进行操作时，对于机械臂工作端运动的控制就显得非常关键。机械臂控制问题的基础是对其动力学特性的准确分析，关于移动式救援机器人系统的动力学问题有很多的研究方法，其中比较著名的有：拉格朗日方程、凯恩方程以及牛顿-欧拉方程等[5-8]。

国内外学者对移动式救援机器人的控制问题进行了大量的研究[9-10]。李志军[11]等人基于力控制思想，提出了一种移动式机械臂的自适应-鲁棒控制算法。Wang等人[12]研究了考虑未知动力学影响时移动式机械臂的运动/力控制问题。S.Lin[13]等人针对移动式机械臂的轨迹控制问题，提出了一种神经网络控制算法。A. Hassam[14]等人针对移动机械臂系统的平台存在缓慢、不准确动力学响应时，提出了一种模糊运动学控制算法。

首先对移动式救援机器人的建模问题进行了研究，得到了相应的运动学与动力学方程，根据该方程研究了移动式救援机器人的动力学仿真问题。其次，以得到的动力学模型为基础，研究了移动式救援机器人工作端轨迹的跟踪控制问题，设计了相应的控制策略；最后，以一个两关节的移动式救援机器人系统为例，对本文用到的运动学、动力学模型与控制算法进行了仿真验证。

1 救援机器人的系统建模

对移动式救援机器人系统进行研究的基础是建模问题，建模问题的实质就是对救援机器人系统的运动学与动力学问题进行研究。本文研究的救援机器人系统是一个移动式机械手臂系统，如图1所示。救援机器人系统由移动基座与n关节机械臂组成，各关节由转动铰连接。本文主要采用的三个坐标系分别是：惯性坐标系(以轨道上的某一点为圆点)、基座坐标系(以移动基座为原点)及局部坐标系(以机械臂各关节旋转轴为z轴)。移动式救援机器人工作端的运动学关系式如下：

(1)

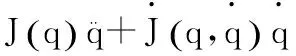
(2)

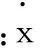
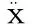
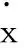
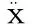
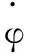
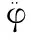
JB——移动基座变量的雅克比矩阵；

Jφ——机械臂关节转铰变量的雅克比矩阵。

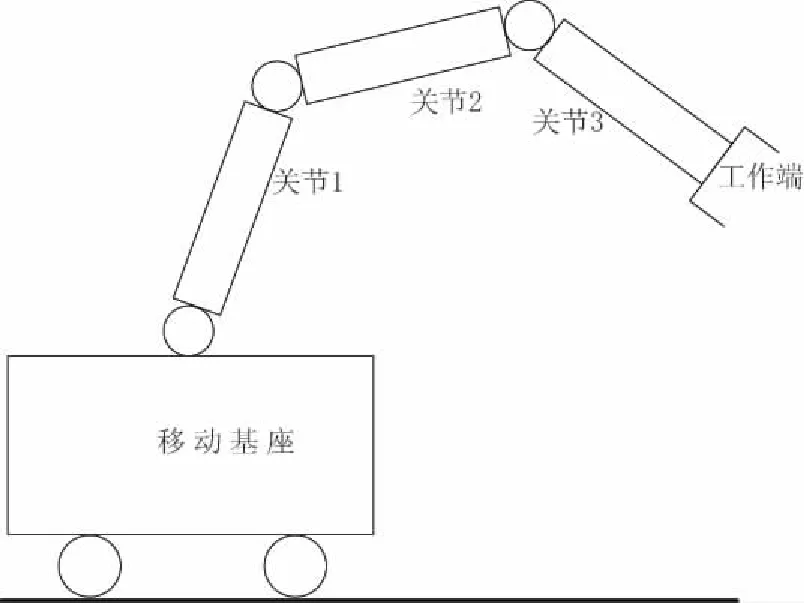
图1 救援机器人系统模型

由于本文研究的救援机器人系统，是一个典型的多刚体系统，而研究多刚体系统动力学的方法很多，其中以拉格朗日乘子方程最为常用，采用该方法得到的救援机器人系统动力学方程如下：

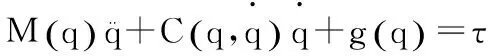
(3)

式中各符号的物理量的意义如下：

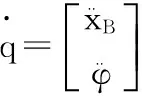
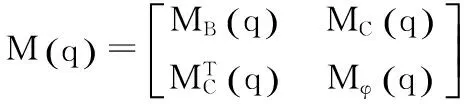
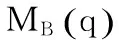
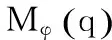
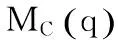
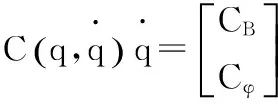
CB为移动基座的离心力、哥氏力项；

Cφ为机械臂的离心力、哥氏力项；

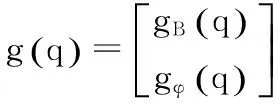
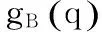
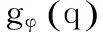
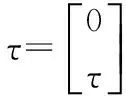
2 动力学分析过程

由式(3)可得：

(4)

式(4)是移动式救援机器人的动力学仿真基础，其具体过程是：

1) 在时间t，计算移动基座、关节1到n的位置和速度；

2) 计算式(4)中各惯性矩阵；

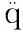
4) 确定控制力τ的控制策略；

6) 将上一步的结果进行积分，得到t+Δt时刻移动基座、关节1到n的位置和速度；

7) 跳转到第一步。

3 机械臂工作端轨迹的跟踪控制

在移动式救援机器人开展救援工作过程中，利用系统机械臂进行相应操作时，需要对机械臂的工作端轨迹进行精确控制，这就需要选择恰当的机械臂控制策略。关于机械臂的控制方法有很多，其中按照所控变量的不同，可分为关节空间控制与操作空间(工作空间)控制。由于机械臂的工作轨迹通常是定义在操作空间内，因此，采用操作空间控制要优于关节空间控制。本文主要基于该控制策略的基本思想来设计机械臂的控制算法。

移动式救援机器人进行目标操作时，机械臂的工作端需要完成期望的轨迹，特别是要实现点对点(初始位置与期望位置)的精确控制。前面得到的移动式救援机器人系统的动力学模型式(3)，可进一步化为：

(5)

式(5)可进一步简化为：

(6)

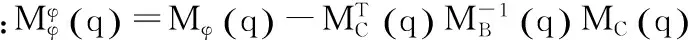
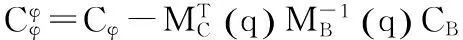
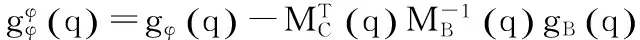
由式(6)可知：

(7)

令：

(8)

将式(8)带入式(6)得：

(9)

根据式(9)，设计逆动力学控制器如下：

(10)

式(10)中的控制输入：

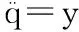
(11)

对于移动式救援机器人工作端轨迹的跟踪控制，主要通过对于机械臂各关节的转角进行控制来实现。利用前面得到的运动学关系式(2)，令新的控制输入为如下形式：

(12)

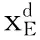
(13)

式(13)就是移动式救援机器人系统在其工作空间内的工作端轨迹误差方程。

4 仿真分析

本节以一个两关节移动式救援机器人系统为例，利用Matlab软件对其进行动力学仿真，该移动式救援机器人系统的具体参数如表1所示。移动式救援机器人执行目标操作时，工作端期望轨迹的起点与终点分别是：[1.8m,1.0m]；[0.0m,1.5m]，仿真时间：T=8s，仿真步长：0.01s。首先是移动基座(m0=500kg)可移动时，得到的仿真结果，如图2所示；其次是增加移动基座质量(m0 = 5000kg)时，得到的仿真结果，如图3所示；最后是将移动基座固定时，得到的仿真结果，如图4所示。

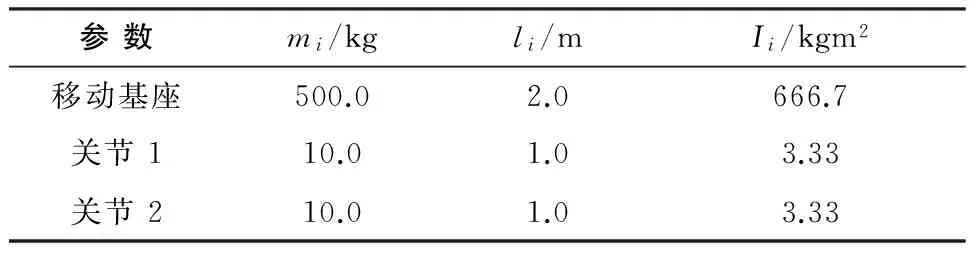
表1 移动式救援机器人系统参数

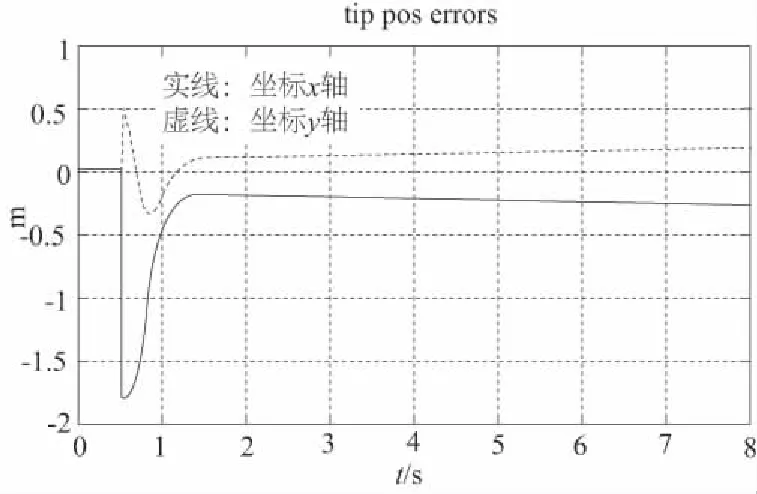
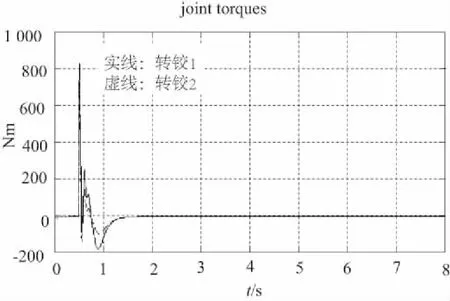
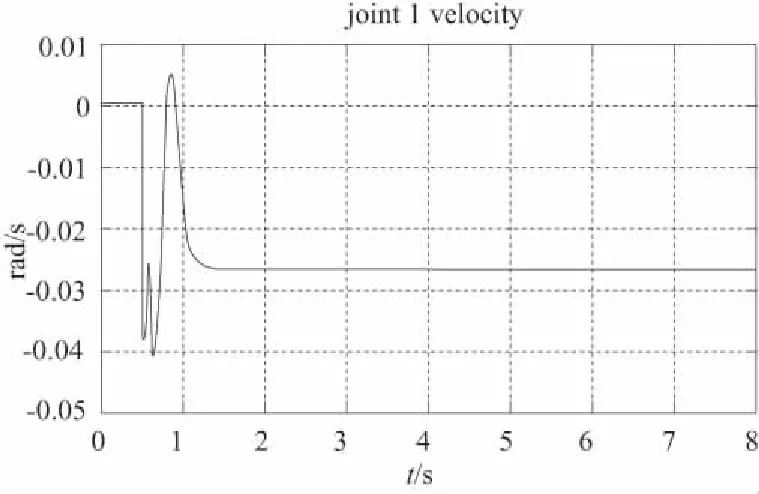
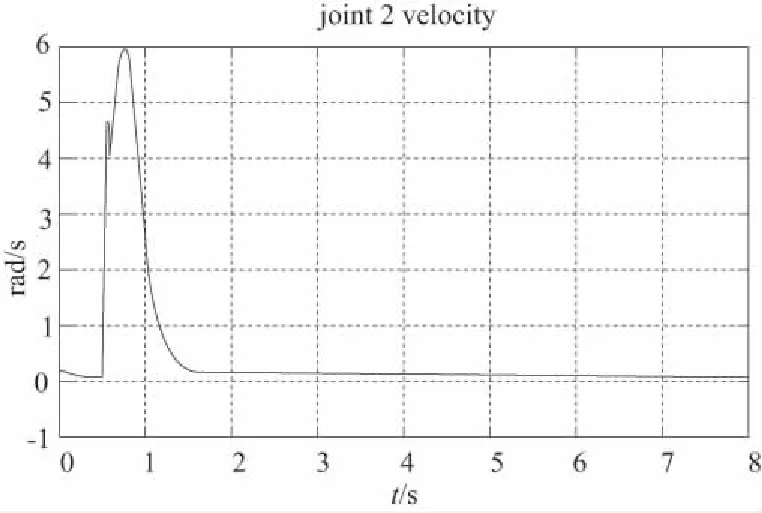
图2 基座移动时工作端跟踪轨迹误差、各关节力矩、各转铰速度

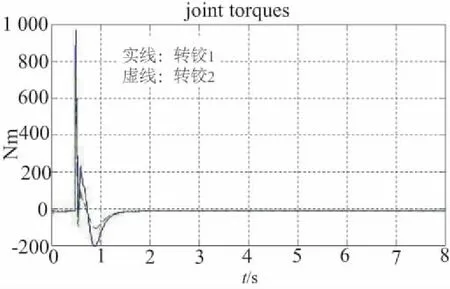
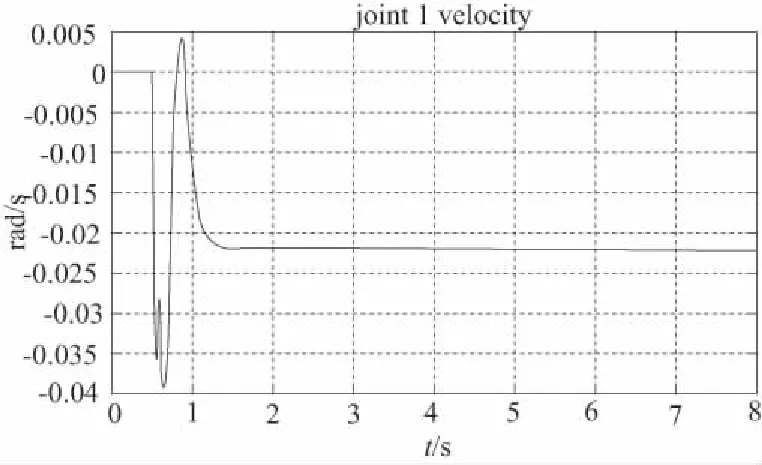
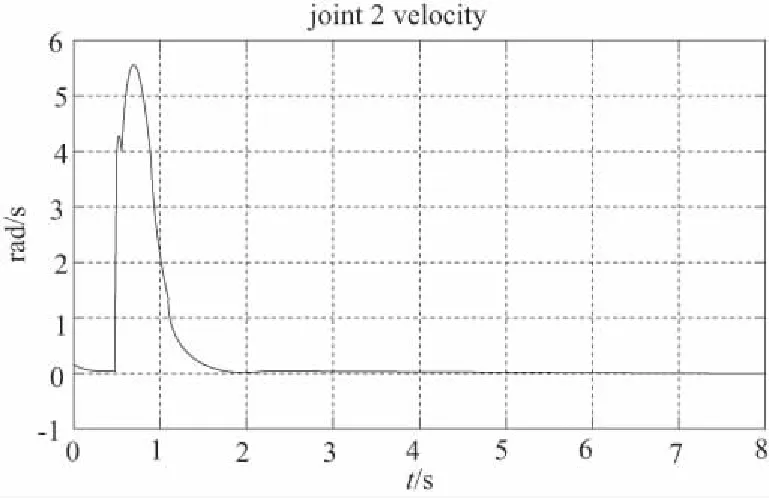
图3 基座移动时工作端跟踪轨迹误差、各关节力矩、各转铰速度(m0=5000kg)

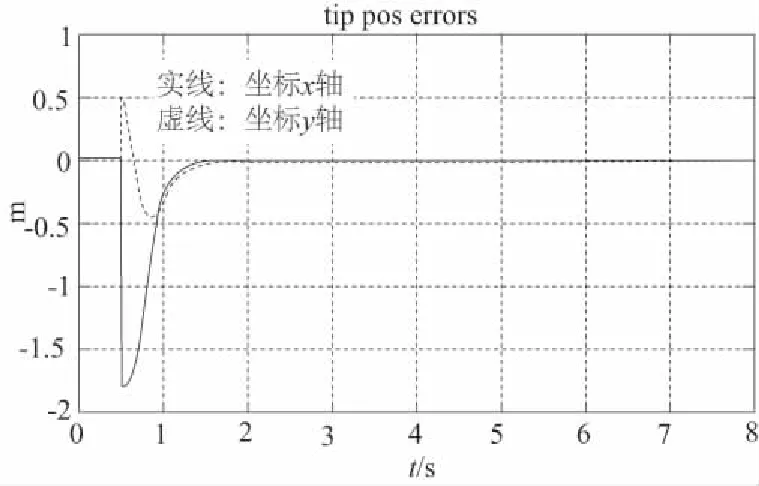
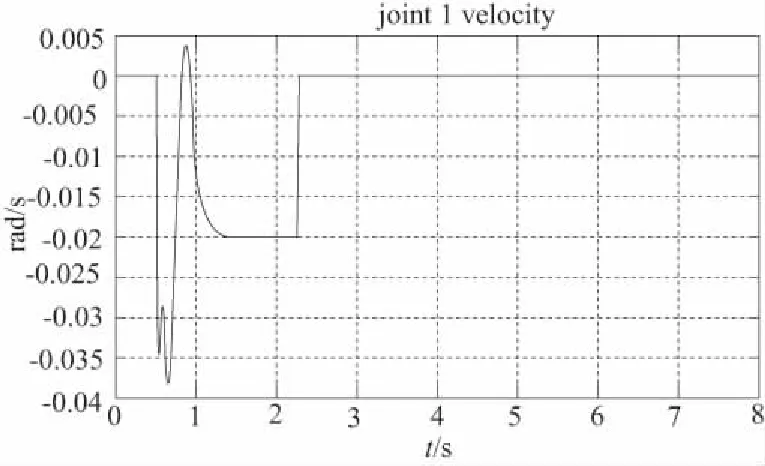
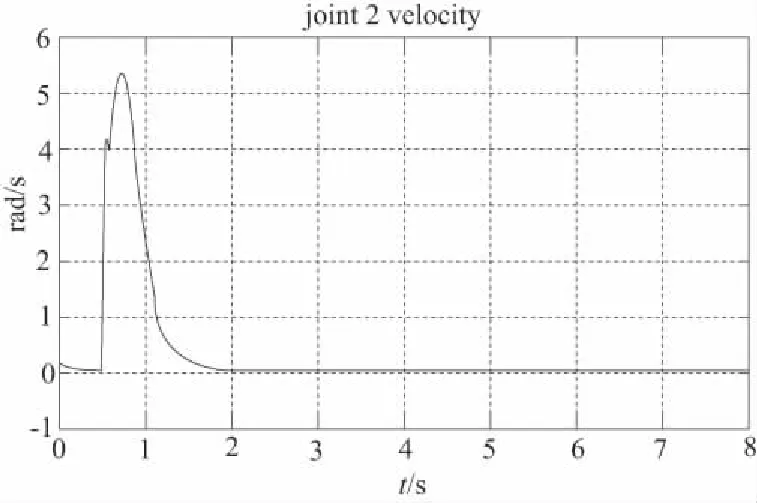
图4 基座固定时工作端跟踪轨迹误差、各关节力矩、各转铰速度

从以上的仿真结果可以得出如下结论：

1) 移动式救援机器人系统的基座可移动时，其工作轨迹的期望值与实际值之间出现一定偏差，且这种偏差随着时间的推移，逐渐变大(图2所示)；提高基座的质量，偏差变小，但逐渐变大的趋势没有改变(图3所示)；当基座固定不动时，偏差趋于零(图4所示)。

2) 观察图2、图3、图4可知，当移动式救援机器人工作端开始跟踪期望轨迹时，机械臂各关节的转速与控制力矩出现较大的突变，但这种突变在本文所提控制算法的控制之下，较短时间内趋于微小值，这表明：本文的控制算法能够有效地保护机械臂关节转铰的驱动电机。

通过以上的仿真结果可知，在移动式救援机器人工作时，将其基座固定在某一位置，利用文中提出的逆动力学控制算法，可以对工作端轨迹实现精确的控制，同时，降低机械臂各转铰速度和控制力矩,当基座不能被固定在某一位置而发生移动时，本文的控制算法同样能够将工作端轨迹的跟踪误差控制在一定范围之内。

结论

对移动式救援机器人执行任务时的运动学、动力学以及控制问题进行了研究，主要分析了移动式救援机器人工作端轨迹的跟踪控制问题，设计了一种操作空间的逆动力学控制算法，通过仿真分析证明，文中所提算法可有效地对工作端轨迹进行控制。

由于移动式救援机器人所处环境的复杂性，移动基座的位置和姿态不一定能够实时的得到保证，同时由于各种未知因素的影响，移动式救援机器人系统的运动学与动力学建模存在着较大的偏差，这就需要在未来的研究中，重点研究移动式救援机器人移动基座与机械臂的协同控制问题、控制算法的自适应问题，以便更好地适应复杂的工作环境。

[1] B. Balaguer,S. Balakirsky. Evaluating maps produced by urban search and rescue robots:lessons learned from RoboCup. Auton Robot, vol 27,pp.449-464,2009.

[2] Brad Hamner, Seth Koterba, Jane Shi,Reid Simmons, Sanjiv Singh. An Autonomous Mobile Manipulator for Assembly Tasks, Auton Robot ,vol 28, pp,131-149,2010.

[3] 陈志华, 钱瑞明.基于ADAMS的救援机器人越障过程分析及仿真[J]. 机械制造与自动化， 2010，39 (1): 157-158.

[4]林小武,钱瑞明,刘巍,等.救援机器人越障过程设计[J].机械制造与自动化，2010，39 (2) : 139-141.

[5] Ata,A.A.Dynamic, Modelling and numerical simulation of a non-holonomic mobile manipulator. International Journal of Mechanics and Materials in Design, 6(3), 209-216. ISSN 1569-1713, 2010.

[6] Mazur,A, Trajectory tracking control in workspace-defined tasks for nonholonomic mobile manipulators. Robotica, 28(01), 57. ISSN 0263-5747, 2010.

[7] Mazur, A, Szakiel, D. On path following control of nonholonomic mobile manipulators. International Journal of Applied Mathematics and Computer Scienc, 19(4), 561-574. ISSN 1641-876X，2009.

[8] Luca, A. D, Oriolo, G, Modeling and control of nonholonomic mechanical systems. In Kinematics and dynamics of multi-body systems. Springer-Verlag, Wien, New-York. ISBN 9783211827314, 1995.

[9] Weimin Ge and Duofang Ye, Sliding Mode Variable Structure Control of Mobile Manipulators, Int. J. Modelling, Identification and Control, Vol. 12, Nos. 1/2, 2011.

[10] S. Djebrani, A.Benali and F. Abdessemed. Modelling and Control of an Omnidirectional Mobile Manipulator. Int.J.Appl.Math.Comput.Sci., vol.22.pp.601-616,2012.

[11] Zhijun Li, Shuzhi Sam Ge and Aiguo Ming. Adaptive Robust Motion/Force Control of Holonomic-Constrained Nohholonomic Mobile Manipulators. IEEE Trans. System, man, and cybernetics., vol. 37, pp. 607-616，2007.

[12] Z.P.Wang, T. Zhou, Y.Mao and Q.J.Chen.Adaptive recurrent neural network control of uncertain constrained nonholonomic mobile manipulators. International Journal of System Science. vol.19,pp.1-12, 2012.

[13] Sheng Lin and A. A. Goldenberg. Neural-Network Control of Mobile Manipulators. IEEE rans. Neural Netw, vol. 12, no. 5, pp. 1121-1133,2001.

[14] A. Hassam and M. Hamani. Motion Control of non-Holonomic Mobile Manipulator using Fuzzy Logic. Proceeding of the 8th Saudi Engineering Conference (SEC8) , Buraydah, Saudi Arabia, Nov. 17-20, 2011.

Dynamic Simulation of Mobile Rescue Robot

ZHANG Xue-jun1，ZHANG Xin1,2, CONG Pei-chao2

(1. College of Mechanical Engineering, Northeast Dianli University, Jilin 132021, China;2. College of Mechanical Engineering, Liaoning Technical University, Fuxin 123000, China)

This article esfablishes the kinematic and dynamic models of mobile rescue robot using the concepts of Jacobian and Lagrange Multiplier Formulation, analyzes its simulation procedure,brings for ward the inverse dynamics control based on the operational space, in order to achieve end-effectors trajectory control and verifies the kinematic, dynamic models and the control strategy.

mobile rescue robot; end-effectors trajectory; simulation analysis; inverse dynamics control

张学军(1960-)，男，吉林人，教授，研究方向为救援机器人。

TP242

A

1671-5276(2014)02-0156-04

2013-02-21