基于Pro/E的采煤机行走机构摆线轮的参数化设计

费淞，陈俊，于广征，沈磊，赵静

(1. 江苏省产品质量监督检验研究院，江苏 南京 210007；2. 中国电子科技集团第二十八研究所 江苏 南京 210007； 3. 南京理工大学 机械工程学院，江苏 南京 210094)

基于Pro/E的采煤机行走机构摆线轮的参数化设计

费淞1，陈俊2，于广征3，沈磊3，赵静3

(1. 江苏省产品质量监督检验研究院，江苏 南京 210007；2. 中国电子科技集团第二十八研究所 江苏 南京 210007； 3. 南京理工大学 机械工程学院，江苏 南京 210094)

根据内外摆线的形成原理，建立了滚筒式采煤机行走机构的摆线轮的理论轮廓线方程，并利用Pro/E软件提供的高级编程语言，建立了适用于采煤机行走机构的摆线轮的参数化实体模型，最后验证了模型的可行性。

摆线轮；采煤机；轮廓线方程；参数化

0 引言

滚筒式采煤机是目前煤矿采煤工作的主力开采设备，滚筒式采煤机行走机构的核心部件为行走轮和销排销齿。摆线齿廓的行走轮(摆线轮)具有牵引性能较好，有较强的适应底板起伏、节距变化的能力[1]，因此被广泛使用。近年来，很多文献对滚筒式采煤机的摆线轮-销轨式行走机构的工作原理及设计计算做了详细的理论分析[1-3]。摆线轮的齿廓由于摆线方程的复杂性无法利用标准的刀具进行共轭切削加工，只能使用成形铣削加工，这就对摆线的齿廓曲线的造型提出了较高的要求[4]。传统的造型方法是利用样条曲线来模拟摆线齿廓，并且每更新一次摆线轮的型号，摆线轮齿廓曲线就要重新设计一次，需要耗费设计人员大量的时间和精力，参数化建模技术能从根本上解决这一问题。本文在介绍了内外摆线的形成原理，建立了采煤机行走机构的摆线轮齿廓曲线的参数方程后，利用Pro/E的高级编程语言，对滚筒是采煤机行走机构的摆线轮进行了参数化建模。

1 内、外摆线的形成原理及参数方程

当一滚圆沿导线作纯滚动时，滚圆上任意点的轨迹称为摆线。当导线为圆时，滚圆在导圆内作纯滚动时，滚圆上的任意点的轨迹曲线称为内摆线[5]，如图1所示。

图1 内摆线形成图

其参数方程为：

(1)

式中：Rb——导圆半径;Rg——滚圆半径;t——滚角。

当滚圆在导圆外作纯滚动时，滚圆上的任意点的轨迹曲线称为外摆线，如图2所示，其参数方程为：

(2)

图2 内摆线形成图

2 摆线轮的理论轮廓线方程

滚筒式采煤机构的摆线轮的齿廓曲线通常由普通外摆线和普通内摆线组成，节圆以上齿廓为外摆线，节圆以下齿廓为内摆线。根据外、内摆线的参数方程经过坐标转化可得到摆线轮的齿廓曲线参数方程。

如图3(a)所示，摆线轮的节圆以上外摆线的曲线方程为：

(3)

式中：R——摆线轮节圆半径，mm；

r1——外滚动圆半径，mm；

α1——外滚动圆沿节圆外表面纯滚动所转过的角度，°；

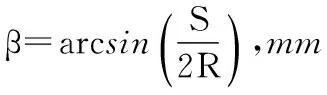
如图3(b)所示，摆线轮的节圆以下外摆线的曲线方程为：

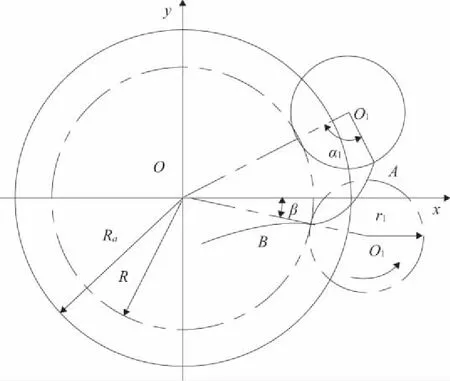
(a)节圆以上外摆线齿廓的形成

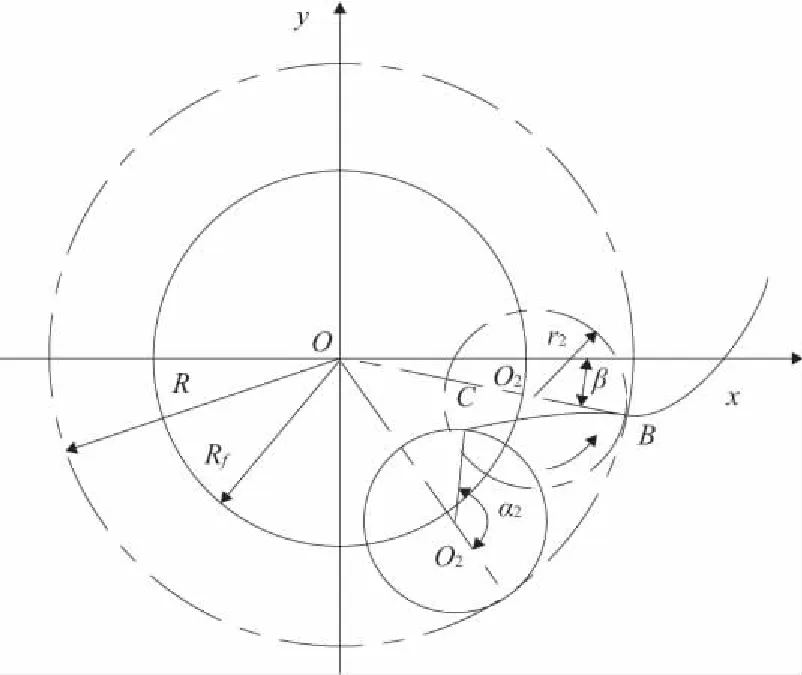
(b)节圆以下内摆线齿廓的形成图3 行走轮摆线齿廓形成图

式中：r2——内滚动圆半径，mm；

α2——内滚动圆沿节圆内表面纯滚动所转过的角度，°。

3 摆线轮的参数化建模

摆线轮的齿廓曲线与形成外、内摆线的节圆、内外滚动圆、齿数有关，齿数Z、节圆半径R、外、内滚动圆半径r1与r2、 模数m和节圆弦齿厚S是在齿廓曲线方程设计中必须确定的独立设计参数，其他与齿廓相关的几何尺寸就可以由计算得出，而要设计出完整的摆线轮，还需要确定齿顶高系数ha、顶隙系数c和齿宽B。

3.1 设置摆线轮齿廓的参数关系

利用Pro/E软件中高级编程语言[6]，首先定义基本参数，如表1；

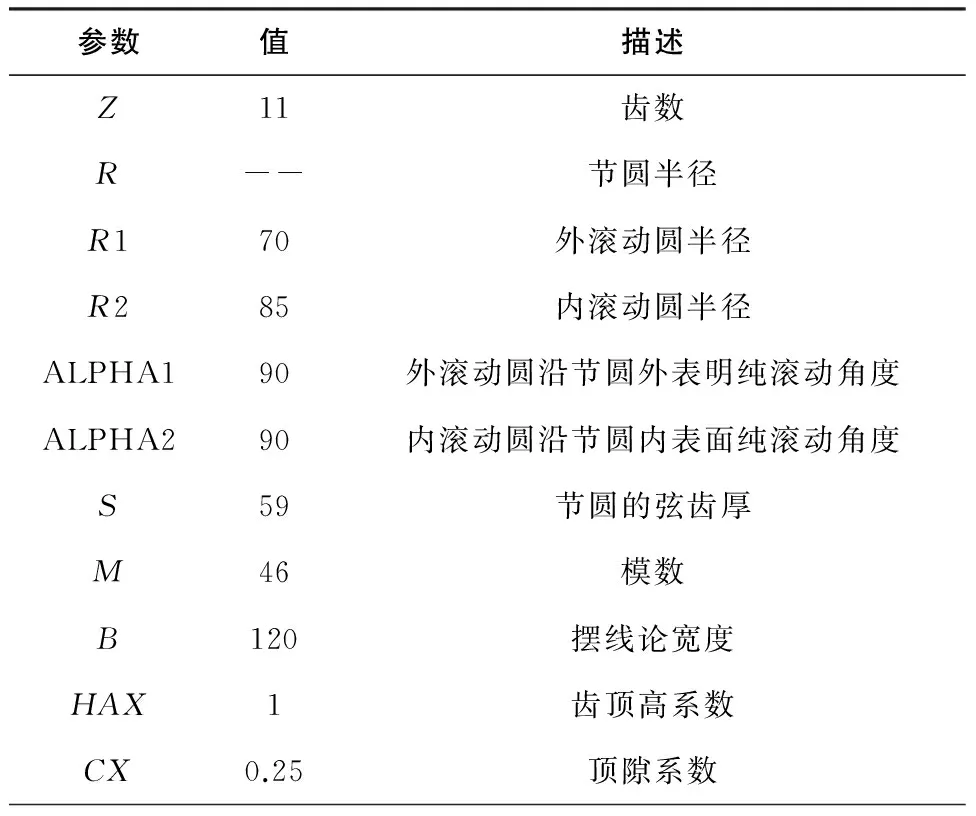
表1 摆线轮基本参数

续表1

RA--齿顶圆半径RF--齿根圆半径R0--齿根过渡圆弧

注：--表示此参数的值是由关系式求出。

再将这些参数的关系式编写入“Relation”中，此段程序如下所示：

/*start

/*注：以下程序中出现的未定义的参数是由在建模过程中Pro/E软件提供的中间特征参数

/*基本参数关系

R=M*Z/2

BETA=ASIN(S/2/R)

HA=HAX*M

HF=(HAX+CX)*M

RA=R+HA

RF=R-HF

/*齿宽

D0=B

D1=B

/*齿根圆过渡半径

IF HAX >= 1

D2=0.38*M

ENDIF

IF HAX < 1

D2=0.46*M

ENDIF

/*复制单齿

D4=360/Z

/*阵列齿形

D12=360/Z

P13=Z-1

/*end

3.2 绘制摆线轮齿廓

在Proe/E软件中采用Curve功能，如图4，选取笛卡尔坐标，先根据圆参数式(5)画出节圆、齿根圆和齿顶圆的曲线，再根据摆线轮齿廓外、内摆线参数式(6)和式(7)和Mirror功能，画出摆线轮齿的曲线，见图5。

图4 Curve窗口

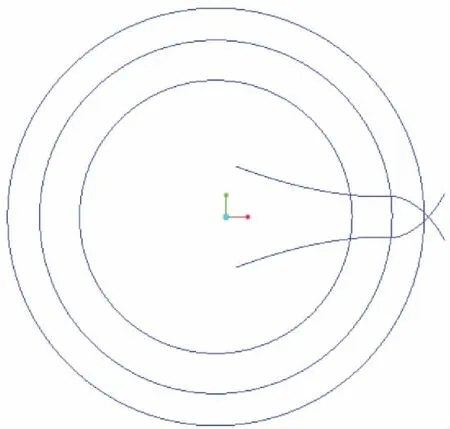
图5 绘制曲线图

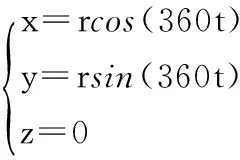
(5)

其中：r分别取R、RA、RF，0

(6)

(7)

先利用Extrude功能拉伸出齿根圆，再利用Sketch中的Use功能拾取所需的轮廓线，将所得的齿形轮廓线进行Extrude功能拉伸，即可得到摆线轮单齿的模型，见图6。在这里，拉伸的深度与摆线轮宽度B进行关联，以便进行尺寸驱动，再依次使用Copy与Pattern功能进行单齿的阵列，最后利用Hole功能得到中心的轴孔，其中只需要注意各个尺寸与摆线轮基本参数的关联，以便能够实现尺寸驱动，如图7。

图6 单齿图

图7 单齿阵列图

3.3 参数化程序设计

程序化工具Program记录着模型的所有特征信息，包括建立过程、参数、尺寸和关系式等信息。设计者只需在Program中的INPUT和END INPUT之间添加经常变更的参数，通过输入新的参数值，驱动模型再生，达到参数化程序设计的目的。对于摆线轮而言，因为在建模时已创建了各参数之间的关系式，所以整个摆线论的特征变化只取决于摆线轮齿数z、模数m、节圆的弦齿长S、外滚动圆半径r1、内滚动圆半径r2、齿宽B、齿顶高系数ha、顶隙系数c和轴孔半径rr1，因此只需添加上述参数的有关语句即可。过程如下：

INPUT

Z NUMBER

"请输入行走摆线轮齿数："

M NUMBER

"请输入行走摆线轮模数："

S NUMBER

"请输入行走摆线轮节圆的弦齿长："

R1 NUMBER

"请输入外滚动圆半径："

R2 NUMBER

"请输入内滚动圆半径："

B NUMBER

"请输入行走摆线轮宽度："

HAX NUMBER

"请输入齿顶高系数："

CX NUMBER

"请输入顶隙系数："

RR1 NUMBER

"请输入轴孔半径："

END INPUT

当需要变更模型时，读取已创建的摆线轮模型，选择再生功能，然后选取需要更改的参数，如图8所示。根据Program的提示依次输入新的参数值，即可生成新的摆线轮，达到了参数化设计的目的，见图9。

图8 初始设计参数输入

(a)七齿摆线轮

(b)九齿摆线轮图9 参数化模型图

4 结论

摆线齿廓的行走轮在滚筒式采煤机的行走机构上的应用较为突出，利用Pro/E软件的造型功能提高了摆线轮齿廓曲线的设计精度，提高了传统造型的齿廓精度；参数化设计有效地提高了设计效率，让设计者在三维造型上花费较少的时间，更方便进行结构尺寸上的优化设计。本文给出的摆线轮摆线齿廓参数方程是准确画出摆线轮三维图形的基础，可为研究和学习行走轮-销轨设计提供合理的理论依据。

[1] 陈伟, 杜长龙, 夏丽建,等. 采煤机行走机构摆线轮设计研究[J]. 煤矿机械, 2010, 31(6): 1-2.

[2] 徐建超, 谭超, 赵亚东. 采煤机行走轮的参数建模与有限元分析[J]. 煤矿机械, 2011, 32(5): 91-92.

[3] 贾传文, 李娜. 简述基Pro/engineer的销齿摆线齿轮三维设计方法[J]. 煤矿机械, 2006, 27(2): 266-268.

[4] 王振乾. 滚筒式采煤机行走机构运动学分析及强度研究[D], 上海：煤科总院上海分院硕士论文, 2007.

[5] 徐义华，等. 摆线泵内转子理论型线参数方程及内外转子的建模[J], 机床与液压, 2008, 36(1): 106-107.

[6] 龙坤，等. Pro/ENGINEERING野火版3.0(中文版)范例练习[M]. 北京: 清华大学出版社, 2006.

Parametric Design of Cycloid Gear for Haulage Mechanism of Shearer

FEI Song1, CHEN Jun2, YU Guang-zheng3,SHEN Lei3, ZHAO Jing3

(1.NART Technology Development Co.,Ltd., Nanjing 210007,China; 2. The 28th Reeearch Institute of CECT Nanjing 210007,China;3. School of Mechanical Engineering, Nanjing University Science & Technology, Nanjing 210094, China)

Based on the forming principles of inner cycloid and outer cycloid, the parametric equation for the cycloid gear of the haulage mechanism of the drum shearer, is established. Then, by using the advanced programming function of Pro/Engineering, its practical parametric model is set up. At last, the feasibility of this parametric model is demonstrated lay two examples.

cycloid gear;shearer;theoretic profile curve;parametric

费淞(1980-)，男，江苏溧阳人，工程师，学士，主要研究方向:工业自动化。

TH12

B

1671-5276(2014)02-0108-05

2013-01-23