Spectral Shift of π→π∗Transition for p-Nitroaniline Based on a New Expression of Nonequilibrium Solvation Energy
2014-07-18JinLiHishengRenJinyiXingyunLi
Jin Li,Hi-sheng Ren,Jin-yi M,Xing-yun Li
a.College of Chemistry,Sichuan University,Chengdu 610064,China
b.Institute of Atomic and Molecular Physics,Sichuan University,Chengdu 610065,China
c.College of Chemical Engineering,Sichuan University,Chengdu 610065,China
(Dated:Received on October 31,2013;Accepted on February 10,2014)
Spectral Shift of π→π∗Transition for p-Nitroaniline Based on a New Expression of Nonequilibrium Solvation Energy
Jian Lia,Hai-sheng Rena,Jian-yi Mab,Xiang-yuan Lic∗
a.College of Chemistry,Sichuan University,Chengdu 610064,China
b.Institute of Atomic and Molecular Physics,Sichuan University,Chengdu 610065,China
c.College of Chemical Engineering,Sichuan University,Chengdu 610065,China
(Dated:Received on October 31,2013;Accepted on February 10,2014)
According to the nonequilibrium solvation theory studies,a constrained equilibrium principle is introduced and applied to the derivations of the nonequilibrium solvation energy, and a reasonable expression of the spectral shift of the electronic absorption spectra is deduced.Furthermore,the lowest transition of p-nitroaniline(pNA)in water is investigated by time-dependent density functional theory method.In addition,the details of excited state properties of pNA are discussed.Using our novel expression of the spectral shift,the value of-0.99 eV is obtained for π→π∗transition in water,which is in good agreement with the available experimental result of-0.98 eV.
Nonequilibrium solvation theory,Spectral shift,Solvent reorganization energy, Constrained equilibrium
I.INTRODUCTION
p-Nitroaniline(pNA)is a common compound used as an intermediate or precursor in the manufacture of organic synthesis,such as p-phenylenediamine,azo dyes, antioxidants,fuel additives,pharmaceutical synthesis, etc.[1].This molecular has a large f i rst hyperpolarizability,and it is efficacious in second-harmonic generation with possible applications in photonic devices, telecom-munications and signal processing[2].The simple structure of pNA and its particular nonlinear optical properties make it a convenient model for theoretical studies of the solvent-solute interactions and solvation of the electronic states.Especially,due to its important role in prototypical organic push-pull(donorπ-acceptor)chromospheres,it is of great interest for researchers in both theoretical[3-11]and experimental[12-15]investigations.Therefore,the exited state properties of pNA have been a hot topic for researchers in recent years.
It is found that the lowest singlet excited state which is associated with an intramolecular charge transfer from the electron-donor amino group(NH2)to the electron acceptor nitro group(NO2)across the phenyl ring will lead to a change in the dipole moment of pNA[7,8]. During this process,pNA undergoes a strong π→π∗absorption band in the near-ultraviolent to visible spectral region[8].Its peak is strongly dependent on the solvent polarity due to the increase of the dipole moment[2, 12].Experimentaly,a larger spectral shift of-0.98 eV in water is observed by ultrafast transient absorption spectroscopy[12-14].Theoretically,using QM/MM (CIS(D)/EFP)approach,Kosenkov et al.predicted the spectral shift of π→π∗transition is-1.00 eV in water[5].More recently,Gordon et al.studied the spectral shifts of pNA with TD-B3LYP/DH(d,p),TDPBE0/DH(d,p)and TD-CAM-B3LYP/DH(d,p)methods and obtained the values are-0.60,-0.67,and -0.90 eV for π→π∗transition,respectively[11].We can see the values of π→π∗transition given by using dif f erent theoretical methods have a larger range and are in disagreement with each other[5,11].It is known that accurate theoretical description of spectral shift, that is,condensed phase ef f ect on optical absorption spectra,requires a proper account of nonequilibrium solute-solvent interaction.Therefore,how to set up a correct nonequilibrium state is a great challenge in theory[16].
Recently,under the guidance of Leontovich’s constrained equilibrium principle[17],our group have obtained a new formula for the nonequilibrium solvation energy[18,19].On the basis of this new formula,we have successfully evaluated the reorganization energy of electron transfer reactions[20-23]and vertical ionization energy of hydrated electron[24].In this work, we further develop its application and deduce the novel expression of spectral shift for absorption spectrum.
There are many dif f erent models to be applied for estimating the solvent ef f ects on spectra in solution, such as polarizable continuum model(PCM)[25],quantum mechanics/Monte Carlo(QM/MC)and quantummechanics/molecular dynamics(QM/MD)[26-30].In PCM,the solvent is imitated as a uniform continuous medium,characterized solely by a scalar dielectric constant.This treatment mainly concentrates on the long-range electrostatic interactions between the solute and solvent and can e ff ectively reduce the computational consumption[31-33].QM/MC and QM/MD repute the solvent as individual molecule de fi nitely [26-30].This indicates a supermolecular model where the solvent molecules around the solute are explicitly included in the quantum mechanical calculations.In this premise,they can provide atomic-level structure of the solvent environment and the dynamical change of the system.Furthermore,they can also square up the dispersion-repulsion interactions between the solute and solvent molecules.However,the drawback is that such an approach is computationally very demanding. It would be more expensive if we sample sufficient confi gurations and its accuracy is always signi fi cantly dependent on the potential standing for the solvent[34]. Besides,because the in fl uences of the solvent on the solute are mainly from the fi rst solvation shell,the solvent molecules can hardly be clustered with the solute molecule.This is the problem of a supermolecular strategy to treat with QM method.As for the remaining solvent molecules,the continuous medium theory based on the supermolecular solute can be used to deal with them[35].Up to now,the simplest method is to use the early ideas of Onsager[36]and Kirwood[37]enclosing the solute in a cavity which is surrounded by a polarizable dielectric continum[38-41].
In this work,we fi rst brie fl y introduced the new theory of nonequilibrium solvation,i.e.constrained equilibrium approach is adopted in the continuum model to deal with the nonequilibrium solvation.Then we apply the new theory to single-sphere model and obtain the new expression for the absorption spectral shift.We also presented the computational details,the calculated results are compared with the previous theoretical and experimental results.
II.THEORETICAL METHODS
A.Nonequilibrium solvation
In the framework of continuous medium theory,we carry all the following derivations with charge-potential representation.Our work just cares about the electrostatic contribution to the solvation energy.When it comes to an ultrafast process in solution,such as light absorption and emission,the vertical detachment of a hydrated electron,or electron transition of electron transfer at the transition state,as shown in Fig.1,the solute-solvent system will undergo a change from the equilibrium state 1[ρ1,](where ρ1andstand for the solute charge and solvent polarizatpotential in equilibrium state 1)to the nonequilibrium state 2[ρ2,](where ρ2andstand for the solute charge and the polarization potential in nonequilibrium state 2).Along with a long enough time to prepare,the nonequilibrium state 2[ρ2,]will become the equilibrium state 2[ρ2,.These processes can be shown in Fig.1.

FIG.1 A generic schematic diagram for the constrained equilibrium approach.
We regard the solvent medium as the“system”and treat the others consisting of the solute charges and the constraining charges as the“ambient”.Thus,the electrostatic solvation energy expression for the f i nal equilibrium state 2,shown as follows:

We add the external(constraining)charge ρexlin-reversible path because the solvent polarization always keeps equilibrium with the solute charge and the external charge.
The work done by the addition of an external f i eld can be expressed ρexas follows:

Please note that ϕeqstands for the equilibrium polarization potential produced by ρ2+ρexin the constrained equilibrium case.The reversible work done during the process from the equilibrium[ρ2,]state to the constrained equilibrium state can be obtained as follows:The constrained equilibrium state can be regard as an equilibrium state.Therefore,we can simply obtain its solvation energy as follows:


When we remove the external charge density ρexsuddenly,the constrained equilibrium solvent system will restore the true nonequilibrium polarization.During this process,the work done by the system is given by

Therefore,the electrostatic solvation energy of the nonequilibrium state can be expressed as follows:

The solvent reorganization energy is def i ned by

Substituting Eqs.(2)and(10)into Eq.(11),we have[21]

where by ρexin the medium with a static dielectric constant εs.So the f i rst two terms in Eq.(11)can of f set.Thus, we can simplify Eq.(11),it is shown as follows:is the equilibrium potential produced
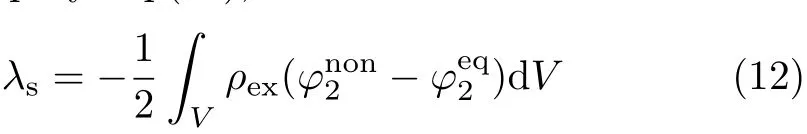
According to our previous ef f orts[18,42,43]

The solvent reorganization energy can be expressed as follows:

here∆ϕsis the solvent polarization potential produced by∆ρ in the medium of εs,∆ϕopis the solvent polarization potential produced by∆ρ=ρ2-ρ1in the medium with the optical dielectric constant εop.

FIG.2 A generic schematic depiction of solvent ef f ect of absorption spectra in aqueous solution.
B.Spectral shift with point dipole in a sphere cavity
In Fig.2,we denote 1 and 2 standing for ground state and excited staterespectively.The Ui(g)(i=1,2)standsgies of the equilibrium ground state 1,nonequilibrium excited state 2,and equilibrium excited state 2,respectively.The absorption spectral shift is de fi ned as the solvation energy di ff erence between nonequilibrium excited state 2 and equilibrium ground state 1[44,45]. So it can be expressed as

Obviously,the energy of the nonequilibrium solvation energy can be expressed by the energy of the equilibrium excited state plus solvent reorganization energy. The solvation energies for the equilibrium state and excited states can be expressed as follows:

where ϕ and ρ stand for the polarization potential and the charge density of the solute,λsstands for the solvent reorganization energy.
With Eqs.(16)-(20),we can get the general form for the absorption spectral shift as:

Here,we use Onsager[36]point dipole as a sphere cavity model and assume that solute charge is distributedin the center of point dipole in a vacuum sphere cavity.The radius of a spherical cavity is a.The cavity is surrounded by dielectric constant εsof the solvent. Optical excitation process makes the dipole moment of the solute change from the ground state~µ1to excited state~µ2.
The dipole moment can be given by:

where L is the distance pointing from q+to q-.The polarization potential inside the sphere cavity is as follows:[19,46,47]

In order to satisfy the constrained equilibrium state,we need add the external control dipole moment i.e.[19, 46,47]

Here∆µ=~µ2-~µ1presents the dipole change.
With Eqs.(15),(23),and(24)and the relationship E=-▽ϕ,we can obtain the solvent reorganization energy expression as

Here we use the relationship as follows[19,46,47]:

We consider L is too small.Thus,we have:

The energy of the equilibrium solvation can be expressed as

Here we use the following expression[19,46,47]

Combining Eqs.(21),(25),and(29),we can obtain the f i nal form for the absorption spectral shift with single sphere and point dipole approximation i.e.

III.COMPUTATIONAL DETAILS
In this work,p-nitroaniline(Fig.3)is chosen to investigate the spectral shift of the electronic absorption spectrum of the lowest π→π∗transition in aqueous solvent.The optimized geometry of pNA in vacuum and in aqueous solvent were obtained at density functional theory(DFT)[48]level with the PBE0[49-51],B3LYP [52]functional and cc-pVDZ basis set using the Gaussian program package[53].These two functionals give similar results.In order to stay the same as the following calculations,the one with the B3LYP[52]functional was utilized for the following calculations.In addition to the detailed structural study of the molecular,the theoretical values of the vertical excitation energy and dipole moments in vacuum were investigated with the gas phase geometry.The calculations in water were adopted from the geometry optimized in aqueous solution.The various excited states were calculated at the same levels using time density functional theory (TDDFT)[51,52]method and B3LYP functional for gas phase and condensed phase,respectively.Though this method of calculations has some restrictions and disadvantages,it has been shown to provide excitation spectra in very good agreement with experimental results.

TABLE I Geometrical parameters of p-nitroaniline both in vacuum and water along with available experiment results(bond length in˚A,angles in(◦)).

TABLE II Dipole moments for ground state S0and the Franck-Condon excited states S2,S1due to the solvent ef f ects(unit in Debye)in vacuum and water,together with the experimental data and other theoretical results.

FIG.3 Structure for pNA with the labeling of atoms used in the text(bond lengths and angles are given in Table I).
IV.RESULTS AND DISCUSSION
A.Molecular properties
In order to interpret the excited state charge transfer properties of pNA,optimized geometry and charge distributions of pNA in their ground state are obtained at DFT level using B3LYP[52]functional and cc-pVDZ basis set.It gives a planar structure for pNA in Fig.3. We list the average geometric parameters for the gas phase structure of pNA of the ground state in Table I. Some dif f erent theoretical results and the available experimental data[15]are also collected in Table I.It can be seen that our calculations are very close to the experimental data from Table I.The dif f erences between the calculated and experimental parameters do not exceed 0.02˚A for bond lengths and 1.5◦for bond angles. Therefore,this optimization is perfect and it has formatted a very stable structure.Furthermore,we can get the excitation energies and dipole moments on the basis of this structure.
The calculated dipole moments for ground state S0, the second excited state S2in gas phase,and ground state S0,the f i rst excited state S1in condensed phase are shown in Table II,along with some available theoretical results[4,11]and experimental observations [6-8].It can be seen that our calculated dipole moments are close to the experimental results,respectively [6-8].They also approximate to other theoretical results[4,11].

FIG.4 HOMO and LUMO frontier orbitals involved in the lowest π→π∗electronic transition.
The highest oscillator strength occurs in S2(0.31)excited state for gas phase and in S1(0.59)excited state for condensed phase.Both of their orbital transitions are HOMO→LUMO.From the orbital transition,transition energies and oscillator strengths,it is seen that the f i rst excited state in water corresponds to the second excited state in the gas phase;solvation pulls this charge-transfer state below the other excited states because of its high dipole moment.HOMO and LUMO for pNA are illustrated in Fig.4.It is obvious that the HOMO→LUMO excitation has a π→π∗transition character.The electronically excited state is characterized by intramolecular charge transfer from the NH2to the NO2group.
B.Vertical excitation energy
The vertical excitation energy(VEEs)of the π→π∗transition in gas phase is 4.12 eV with oscillator strength of 0.31 in this work.Other theoretical results calculated with TD-B3LYP/DH(d,p)[11],TDPBE0/DH(d,p)[11],and CIS(D)[6]were 3.97,4.11, and 4.40 eV,respectively,and the available experimental datum was 4.24 eV[12].The theoretical π→π∗transition energy of 4.12 eV is in good agreement with the experiment(4.24 eV),with an error of 0.12 eV.Other theoretical results about the π→π∗transition energy have an error at the same scale[5,11].It fully shows that the B3LYP/cc-pVDZ method is appropriate and good enough to deal with this kind of absorption spectrum.
C.Solvatochromic shift in water
基于统一潮流模型的电-气耦合综合能源系统静态灵敏度分析//骆柏锋,穆云飞,赵波,余晓丹,贾宏杰,周金辉//(13):29
From Eq.(31),it is easy to recognize that the spectral shift is sensitive to the cavity radius.Therefore, it is very important for us to get a reasonable radius. In general,the cavity radius of a spherical molecule in solution may be estimated from the molecular volume Vm,i.e.a0=(3Vm/4π)1/3.Here Vmstands for the molecular volume.In addition,other procedures such as COSMO[54]and PCM[25]can also be applied to estimate the molecular volume.Furthermore,if the solute is considered as a molecule or a supermolecule,the cavity radius size can be estimated according to electron isodensity contour[52-55].It is obvious that we can’t give the true and accurate correction of the cavity radius.Therefore,in this work we do not attempt to give any precise correction of the cavity radius and directly calculate from a0=(3Vm/4π)1/3.Vmis computed for global minimum optimized structure of pNA at DFT level using B3LYP functional and cc-pVDZ basis set.In this way,the obtained cavity radius of pNA is 3.53˚A.
The spectral shift of the π→π∗transition for pNA in aqueous solvent employing Eq.(31)based on our new form of the electrostatic solvation energy for the nonequilibrium polarization is obtained.Our evaluation for the π→π∗red shift is-0.99 eV,which is quite in good agreement with the experimental result of-0.98 eV[12-14].But the theoretical results from TD-PBE0/DH(d,p)and TD-B3LYP/DH(d,p)methods with values of-0.67 and-0.60 eV[11]are underestimated compared with the experiment value;while the values-1.00 and-0.90 eV calculated by CIS(D)[6] and TD-CAM-B3LYP/DH(d,p)[11]were close to the experiment value of-0.98 eV[12-14].These dif f erent results are leaded by employing dif f erent processing methods.On the other hand,though-1.00 eV is very close to the experiment value,the experimental vertical excitation energies in gas and condensed phase for the singlet charge transfer state are overestimated by 0.41 and 0.39 eV,respectively.
pNA is a polarizable molecule,it has strong electrostatic interactions with the surrounding polar water molecules.In fact,solvatochromic shifts of vertical excitation energies may be inf l uenced by specif i c solute-solvent short-range dispersion/repulsion interactions,the solute geometry distortion,the long-range electrostatic and mutual polarization interactions between the solute and solvent molecules.The contribution of dispersion/repulsion interactions is not always considered in many spectra solvation models[56,57] because of its nearly equal contribution to both the states before and after the Franck-Condon transition in strong polar solvents.According to the QM-EFP intermolecular interaction energy analysis of DeFusco et al.[58],the solvent shift is divided into four parts:solute relaxation,Coulomb,polarization,and remainder. The solute relaxation energy is used to def i ne the contribution to the changes of the solvent shift from the condensed phase to the gas phase.And from our calculations,the solute equilibrium geometric parameters in water are dif f erent from those in vacuum.Therefore,in Eq.(31),we have considered this dif f erence.The contributions from the Coulomb,polarization and remainder are discussed by Gordon et al.[11].It is reported that the solvent shift of the π→π∗transition in pNA arises mainly from a change of the electrostatic interaction between solvent and solute upon photoexcitation.In their work,the Coulomb interaction between pNA and water makes the largest contribution to the calculated red shift.In addition,the increased dipole moment of pNAgoing from the gas phase to the condensed phase makes a stronger Coulomb contribution.In our new theory of nonequilibrium solvation,the electrostatic component is also primarily considered.That is why Eq.(31)can well reproduce the lowest electronic absorption spectra of pNA in aqueous solution.
V.CONCLUSION
In the framework of classical thermodynamics,a new expression of the electrostatic solvation energy and solvent reorganization energy for the nonequilibrium polarization is derived based on the constrained equilibrium approach in this work.The charge density and solvent polarization potential have been used to describe the modif i ed expression for the solvent reorganization energy.It is equivalent to the one represented by electric f i eld and polarization.Thus,a novel and reasonable expression of the spectral shift of the electronic absorption spectra has been proposed with the approximation of point dipole and sphere cavity(Eq.(31)).
In order to verify the correctness of the new theory, pNA is chosen as the typical test case to investigate the spectral shift of the electronic absorption spectrum of the lowest π→π∗transition in aqueous solvent.The molecule shows a normal Stokes red shift.We have used DFT method to calculate global minima structure and the vertical excitation energy at DFT level to correlate the experimental and other theoretical results. All the calculations employ B3LYP functional and ccpVDZ basis set.We use the equation a0=(3Vm/4π)1/3and obtain the cavity radius is 3.53˚A.The shift evaluated with Eq.(31)is-0.99 eV for the π→π∗transition. It agrees well with the available experiment result.The electrostatic plus polarization interactions between solute and solvent make important contributions to the spectral shift of pNA in water.Our solvation theory precisely focuses on these interactions,so the spectral shift expression within continuum model can well reproduce the spectra shift of pNA.
VI.ACKNOWLEDGMENTS
This work was supported by the National Natural Science Foundation of China(No.91016002).
[1]J.H.Sun,S.P.Sun,M.H.Fan,H.Q.Guo,L.P.Qiao, and R.X.Sun,J.Hazard Mater.148,172(2007).
[2]V.M.Farztdinov,R.Schanz,S.A.Kovalenko,and N. P.Ernsting,J.Phys.Chem.A 104,11486(2000).
[3]C.Daniel and M.Dupuis,Chem.Phys.Lett.171,209 (1990).
[4]S.P.Karna,P.N.Prasad,and M.Dupuis,J.Chem. Phys.94,1171(1991).
[5]D.Kosenkov and L.V.Slipchenko,J.Phys.Chem.A 115,392(2011).
[6]H.K.Sinha and K.Yates,Can.J.Chem.69,550 (1991).
[7]H.K.Sinha and K.Yates,J.Am.Chem.Soc.113,6062 (1991).
[8]I.Benjamin,Chem.Phys.Lett.287,480(1998).
[9]F.Sim,S.Chin,M.Dupuis,and J.E.Rice,J.Phys. Chem.97,1158(1993).
[10]G.Scalmani,M.J.Frisch,B.Mennucci,J.Tomasi,R. Cammi,and V.Barone,J.Chem.Phys.124,094107 (2006).
[11]S.Sock,S.Y.Willow,F.Zahariev,and M.S.Gordon. J.Phys.Chem.A 115,9801(2011).
[12]S.Millef i ori,G.Favini,A.Millef i ori,and D.Grasso, Spectrochim.Acta 33A,21(1977).
[13]C.L.Thomsen,J.Thøgersen,and S.R.Keiding,J. Phys.Chem.A 102,1062(1998).
[14]S.A.Kovalenko,R.Schanz,V.M.Farztdinov,H.Hennig,and N.P.Ernsting,Chem.Phys.Lett.323,312 (2000).
[15]K.N.Trueblood,E.Goldf i sh,and J.Donohue,Acta Crystallogr.14,1009(1961).
[16]J.Tomasi,B.Mennucci,and R.Cammi,Chem.Rev. 105,2999(2005).
[17]M.A.Leontovich,Introduction to Thermodynamics. Statistical Physics,Moscow:Nauka,99(1983).
[18]X.Y.Li,F.C.He,K.X.Fu,and W.J.Liu,J.Theor. Comput.Chem.9,23(2010).
[19]X.Y.Li,Q.Zhu,F.C.He,and K.X.Fu,Extension of Classical Thermodynamics to Nonequilibrium Polarization,Rijeka:InTech,205(2010).
[20]X.Y.Li,Q.D.Wang,J.B.Wang,J.Y.Ma,K.X. Fu,and F.C.He,Phys.Chem.Chem.Phys.12,1341 (2010).
[21]H.Y.Wu,H.S.Ren,Q.Zhu,and X.Y.Li,Phys.Chem. Chem.Phys.14,5538(2012).
[22]X.J.Wang,Q.Zhu,Y.K.Li,X.M.Cheng,X.Y.Li, K.X.Fu,and F.C.He,J.Phys.Chem.B 114,2189 (2010).
[23]H.S.Ren,Y.K.Li,Q.Zhu,J.Zhu,and X.Y.Li,Phys. Chem.Chem.Phys.14,13284(2012).
[24]J.Xu,Y.K.Li,Q.Zhu,K.X.Fu,and X.Y.Li,Acta Chim.Sin.68,2273(2010).
[25]S.Miertuˇs,E.Scrocco,and J.Tomasi,Chem.Phys.55, 117(1981).
[26]A.Warshel and M.Levitt,J.Mol.Biol.103,227(1976). [27]U.C.Singh and P.A.Kollman,J.Comput.Chem.7, 718(1986).
[28]M.J.Field,P.A.Bash,and M.Karplus,J.Comput. Chem.11,700(1990).
[29]J.Gao,F.J.Luque,and M.Orozco,J.Chem.Phys. 98,2975(1993).
[30]J.Gao,K.B.Lipkowitz,and D.B.Boyd,Editors Reviews in Computational Chemistry,New York:Wiley, 119(1995).
[31]B.Mennucci and R.Cammi,Continuum Solvation Models in Chemical Physics:From Theory to Applications,UK:Chichester,(2007).
[32]N.A.Besley and J.D.Hirst,J.Am.Chem.Soc.121, 8559(1999).
[33]J.Tomasi,B.Mennucci,and R.Cammi,Chem.Rev. 105,2999(2005).
[34]M.Pavone,O.Crescenzi,G.Morelli,N.Rega,and V. Barone,Theor.Chem.Acc.116,456(2006).
[35]P.Bandyopadhyay,M.S.Gordon,B.Mennucci,and J. Tomasi,J.Chem.Phys.116,5023(2002).
[36]L.Onsager,J.Am.Chem.Soc.58,1486(1936).
[37]J.G.Kirkwood,J.Chem.Phys.2,351(1934).
[38]O.Tapia and O.Goscinski,Mole.Phys.29,1653 (1975).
[39]J.L.Rivail and D.Rinaldi,Chem,Phys.18,233(1976).
[40]B.Menucci,M.Cossi,and J.Tomasi,J.Chem.Phys. 102,6837(1995).
[41]K.V.Mikkelsen,H.Agren,and J.A.H.Jensen,Chem. Phys.89,3086(1988).
[42]X.Y.Li,J.B.Wang,J.Y.Ma,K.X.Fu,and F.C. He,Sci.China.Ser.B 51,1246(2008).
[43]X.Y.Li,Q.Zhu,F.C.He,and K.X.Fu.Thermodynamics,Extension of Classical Thermodynamics to Nonequilibrium Polarization,Mizutani Tadashi,Ed., Rijeka:InTech,206(2011).
[44]R.A.Marcus,J.Chem.Phy.24,979(1956).
[45]R.A.Marcus,J.Phys.Chem.98,7170(1994).
[46]Y.K.Li,Q.Zhu,X.Y.Li,K.X.Fu,X.J.Wang,and X.M.Cheng,J.Phys.Chem.A 115,232(2011).
[47]Y.K.Li,H.Y.Wu,Q.Zhu,K.X.Fu,and X.Y.Li, Comput.Theoret.Chem.971,65(2011).
[48]E.Runge and E.K.U.Gross,Phys.Rev.Lett.52,997 (1984).
[49]T.Helgaker and P.Jorgensen,J.Chem.Phys.95,2595 (1991).
[50]K.L.Bak,P.Jorgensen,T.Helgaker,K.Ruud,and H. J.A.Jensen,J.Chem.Phys.98,8873(1993).
[51]C.Adamo and V.Barone,J.Chem.Phys.110,6158 (1999).
[52]A.D.Becke,J.Chem.Phys.98,5648(1993).
[53]M.J.Frisch,G.W.Trucks,H.B.Schlegel,G.E.Scuseria,M.A.Robb,J.R.Cheeseman,J.A.Jr.Montgomery,T.Vreven,K.N.Kudin,J.C.Burant,J.M. Millam,S.S.Iyengar,J.Tomasi,V.Barone,B.Mennucci,M.Cossi,G.Scalmani,N.Rega,G.A.Petersson,H.Nakatsuji,M.Hada,M.Ehara,K.Toyota, R.Fukuda,J.Hasegawa,M.Ishida,T.Nakajima,Y. Honda,O.Kitao,H.Nakai,M.Klene,X.Li,J.E.Knox, H.P.Hratchian,J.B.Cross,V.Bakken,C.Adamo,J. Jaramillo,R.Gomperts,R.E.Stratmann,O.Yazyev, A.J.Austin,R.Cammi,C.Pomelli,J.W.Ochterski, P.Y.Ayala,K.Morokuma,G.A.Voth,P.Salvador, J.J.Dannenberg,V.G.Zakrzewski,S.Dapprich,A. D.Daniels,M.C.Strain,¨O.Farkas,D.K.Malick,A. D.Rabuck,K.Raghavachari,J.B.Foresman,J.V.Ortiz,Q.Cui,A.G.Baboul,S.Clif f ord,J.Cioslowski,B. B.Stefanov,G.Liu,A.Liashenko,P.Piskorz,I.Komaromi,R.L.Martin,D.J.Fox,T.Keith,M.A.Al-Laham,C.Y.Peng,A.Nanayakkara,M.Challacombe, P.M.W.Gill,B.Johnson,W.Chen,M.W.Wong, C.Gonzalez,and J.A.Pople,Gaussian 03(Revision D.01),Wallingford CT:Gaussian,Inc.(2004).
[54]A.Klamt and G.Schuurmann,J.Chem Soc.Perkin. Trans.2,799(1993).
[55]J.Autschbach,T.Ziegler,S.J.A.v.Gisbergen,and E. J.Baerends,J.Chem.Phys.116,6930(2002).
[56]A.¨Ohrn and G.Karlstr¨om,Theor.Chem.Acc.117, 441(2007).
[57]N.Roesch and M.C.Zerner,J.Phys.Chem.98,5817 (1994).
[58]A.DeFusco,J.Ivanic,M.W.Schmidt,and M.S.Gordon,J.Phys.Chem.A 115,4574(2011).
∗Author to whom correspondence should be addressed.E-mail:xyli@scu.edu.cn
猜你喜欢
杂志排行
CHINESE JOURNAL OF CHEMICAL PHYSICS的其它文章
- N2O Decomposition over K-Ce Promoted Co-M-Al Mixed Oxide Catalysts Prepared from Hydrotalcite-like Precursors
- Production of BTX through Catalytic Depolymerization of Lignin
- Inf l uence of pH Value on Photocatalytic Activity of Bi4Ti3O12Crystals Obtained by Hydrothermal Method
- Conformations and Metal Ion Affinities of Glutamine Binding with Alkali and Alkaline Earth Metal Cations:an ab initio Study
- Theoretical Study on Dissociation Mechanisms of Di-ethyl Berylliums and Di-t-butyl Berylliums
- Electronic Structures,DNA-binding,SAR,and Spectral Properties of Ruthenium Methylimidazole Complexes[Ru(MeIm)4L]2+(L=iip,tip,2ntz)
