Similarity Solutions of Marangoni Convection Boundary Layer Flow with Gravity and External Pressure*

Similarity Solutions of Marangoni Convection Boundary Layer Flow with Gravity and External Pressure*

ZHANG Yan (张艳)1,**and ZHENG Liancun (郑连存)2
1School of Science, Beijing University of Civil Engineering and Architecture, Beijing 100044, China
2School of Mathematics and Physics, University of Science and Technology Beijing, Beijing 100083, China

This study is focused on a steady dissipative layer, which is generated by Marangoni convection flow over the surface resulted from an imposed temperature gradient, coupled with buoyancy effects due to gravity and external pressure. A model is proposed with Marangoni condition in the boundary conditions at the interface. The similarity equations are determined and approximate analytical solutions are obtained by an efficient transformation, asymptotic expansion and Padé approximant technique. For the cases that buoyancy force is favorable or unfavorable to Marangoni flow, the features of flow and temperature fields are investigated in terms of Marangoni mixed convection parameter and Prantl number.

Marangoni convection, similarity equations, asymptotic expansion, Padé approximant, approximate solution

1 INTRODUCTION

Marangoni flow is induced by surface tension variations along liquid-liquid or liquid-gas interfaces. The interest of scientists in studying Marangoni convection arises from the possibility of material processing in space crafts, where the gravity force is very small in comparison with the thermo-capillary one, so Marangoni effect is of great importance in microgravity science and space processing [1, 2]. Boiling tests in microgravity have shown that the effect of Marangoni flow is significant in microgravity and may be important with gravity [3, 4]. Hong et al. [5] studied the effect of Marangoni convection experimentally under normal and microgravity conditions on the fluid of silicon oils with different viscosities.

Numerous studies on Marangoni flow in various geometries have been reviewed in literature [6-9]. A systematic numerical study on the two-dimensional Marangoni effect in a two liquid layer system was conducted by Mao et al. [10]. Hashim and Sarma [11] used classical linear stability theory to re-examine the onset of oscillatory Marangoni convection in a rotating fluid layer with a deformable free surface for the insulating case. Golia and Viviani [12] obtained similar solution for Marangoni flows with an external pressure gradient. Arafune and Hirata [13] presented a similarity analysis for the velocity profile of Marangoni flow with the surface tension variation linearly related to surface position. Slavtchev and Miladinova [14] presented similarity solutions for surface tension as a quadratic function of temperature. Christopher and Wang [15] showed that the temperature distribution in a vapor bubble attached to a surface and in the liquid surrounding the bubble was primarily due to the heat transfer through the vapor rather than in the liquid and the temperature variation along the surface was not linear but could be described by a power-law function. Al-Mudhaf and Chamkha [16] obtained the numerical solution for magnetohydrodynamic thermosolutal Marangoni convection over a flat surface with heat generation or absorption effects. Zhang et al. [17-19] studied Marangoni convection of Newtonian and non-Newtonian power law fluids with coupled boundary conditions. Sha et al. [20] summarized the experimental and theoretical studies on Marangoni effect. However, little analytical work has been carried out on Marangoni convection with gravity.

This paper presents a similarity solution for Marangoni convection boundary layer, which is along the interface between two fluids and is generated by the Marangoni flow over the surface resulted from an imposed temperature gradient and buoyancy effects due to gravity and external pressure.

2 MATHEMATICAL FORMULATION

Consider a thermal Marangoni boundary layer coupled with buoyancy effects from gravity and external pressure gradient, which is along interface S between two fluids, as shown in Fig. 1.

We make following assumptions. (1) The gravity vector g is along fluid interface S. (2) The flow fields of the two fluids are independent. (3) The curvature of the interface is negligible. (4) The surface tension varies linearly with temperature. (5) The viscous dissipation is negligible. With the Boussinesq approximation, the dimensionless basic equations for the Marangoni boundary layer can be written as

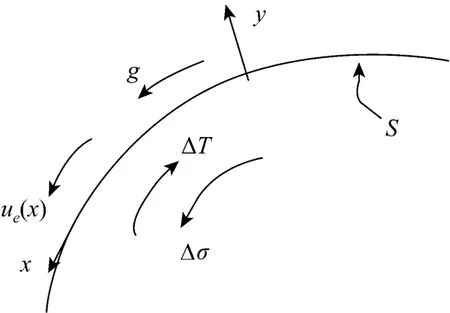
Figure 1 Physical model with interface condition and coordinate system

The boundary conditions are

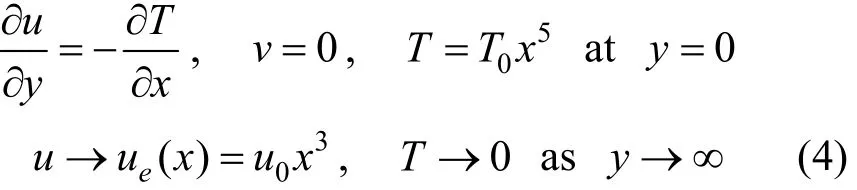
where λ is Marangoni mixed convection parameter, defined as

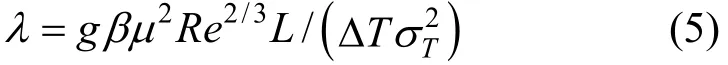
where λ=0 corresponds to forced Marangoni convection flow, studied by Golia and Viviani [12]; parameter Γ has two values: Γ=−1 when buoyancy force is favorable to Marangoni flow and Γ=1 when buoyancy force is unfavorable; and σT=−dσ/dT , with σ assumed as a linear relation

where σmis the surface tension at reference temperature Tm.

Equations (1)-(3) subject to boundary conditions (4) have following similarity variables

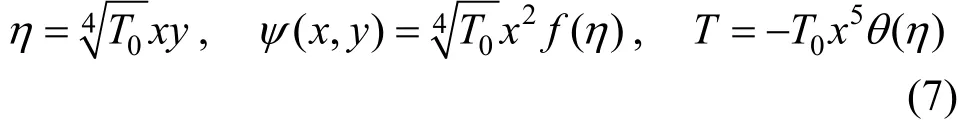
where scale factors u0and T0are chosen to simplify Eqs. (2) and (3) and boundary conditions, such that following relations are satisfied,

Substituting Eq. (7) into Eqs. (1)-(3), we obtain following ordinary differential equations

Boundary conditions (4) become

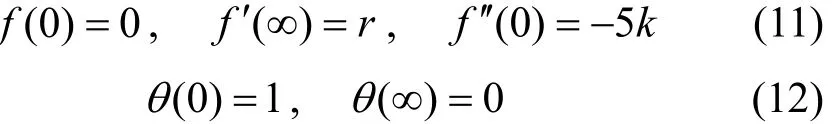
3 SOLUTIONS OF THE SIMILARITY EQUATIONS

To simplify the problem, we only consider r=1 and k=1/5, a′nd other cases′ are similar to this. Weassume that f(0)=a and θ(0)=b and seek the solution in the form of

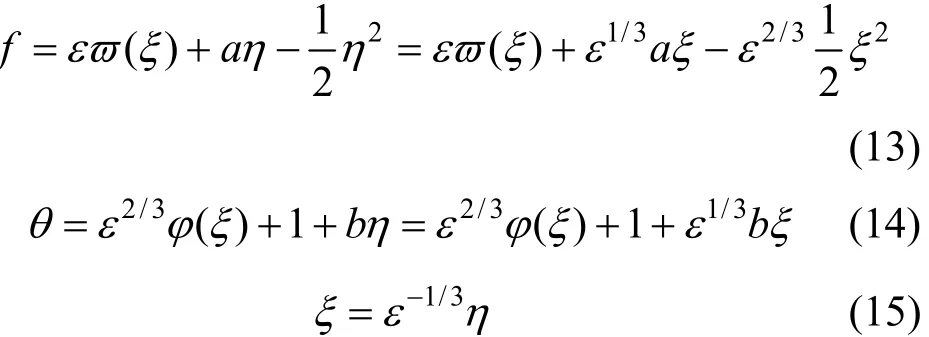
where ε is a small parameter. Substituting Eqs. (13)-(15) into Eqs. (8)-(9), we obtain

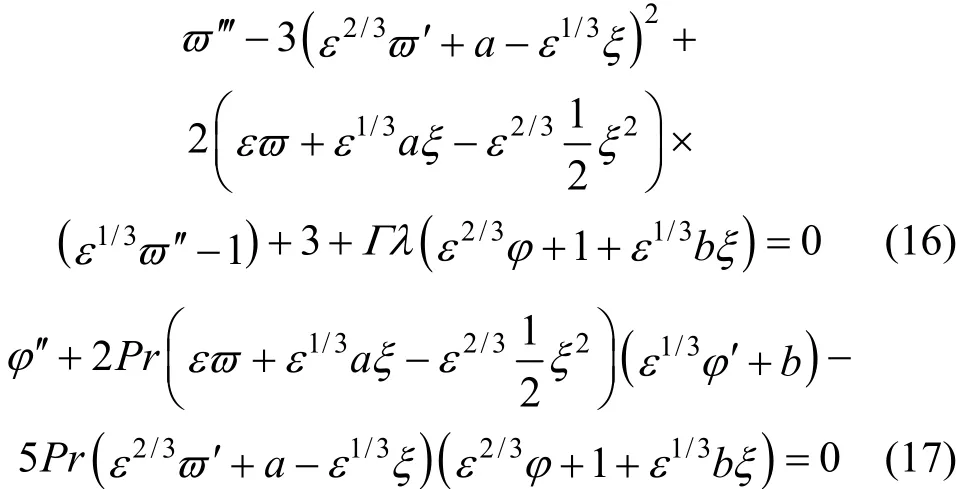
The boundary conditions become

Expanding ϖ and ϕ in a power series near 0ε=,

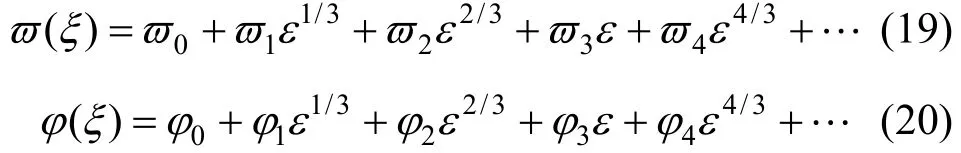
and collecting the coefficients in terms of the power of ε, we obtain

and

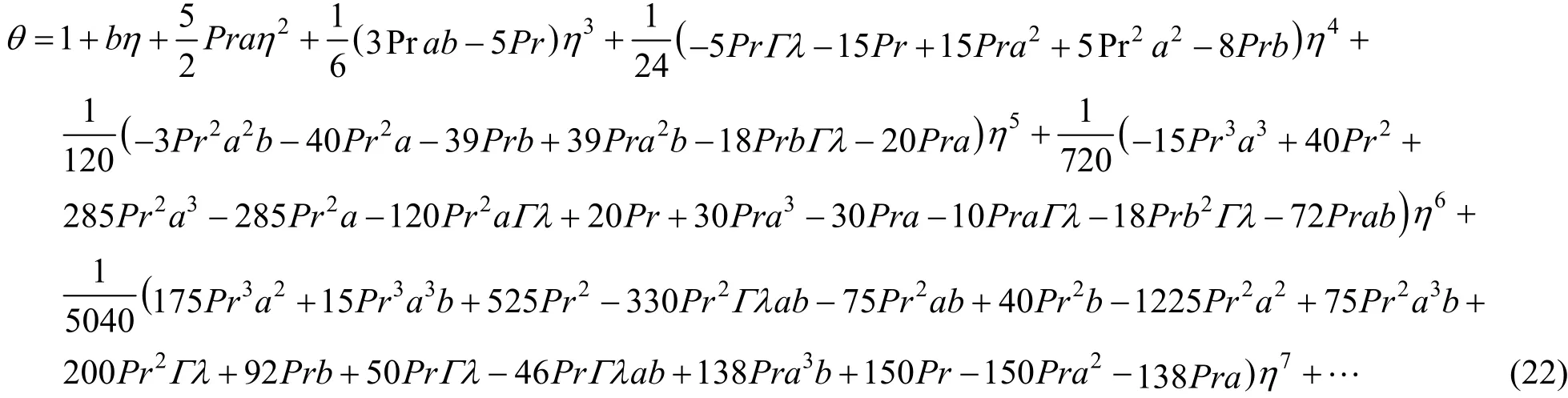
Furthermore, we have

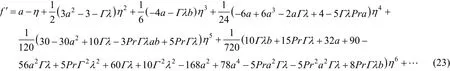
Coefficients a and β can be obtained by Padé approximant technique.

With Padé approximants [2/2] on f′(η)−1 and θ(η), we chooise a0, a1, a2, a3, a4, b1and b2as the coefficients of η (i=0, 1, 2, 3, 4)

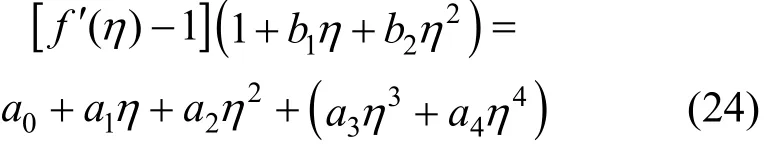
We also choose c0, c1, c2, c3, c4, d1and d2as the coefficients

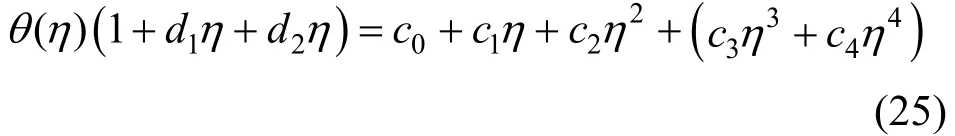
Applying conditions f′(∞)=1 and θ(∞)=0, we have a3=a4=0, c3=c4=0. Substituting Eqs. (23) and (22) into Eqs. (24) and (25), and equating the coefficients, we have

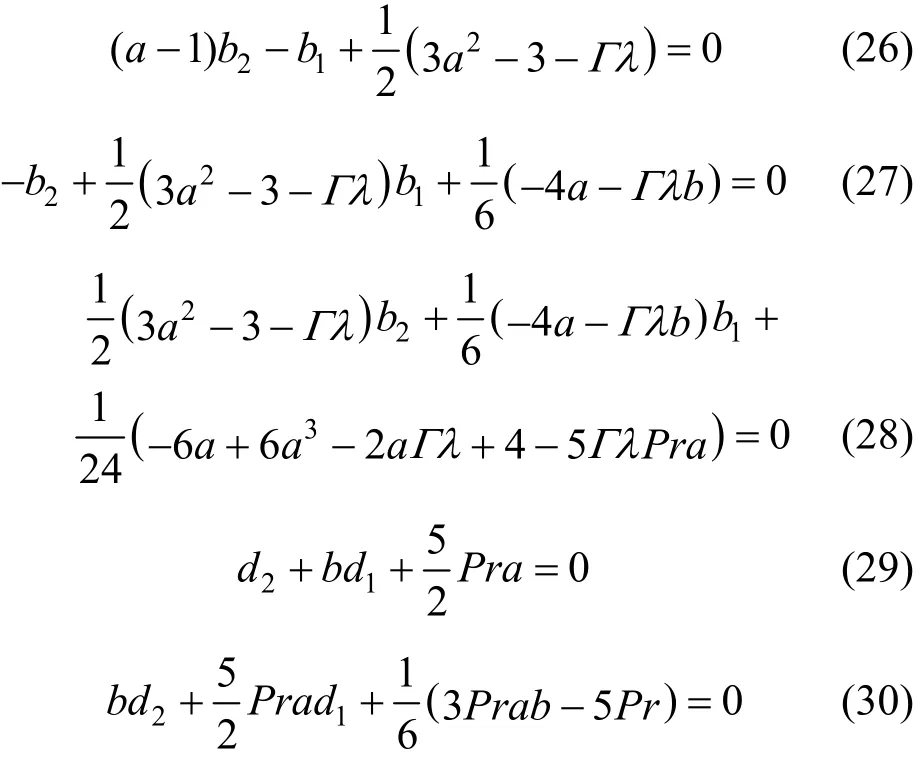
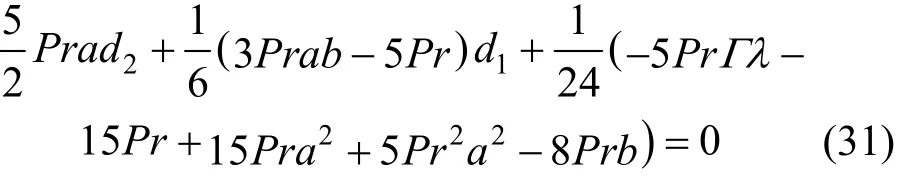
Solving Eqs. (26)-(31), the values of a and b can be obtained.

4 RESULTS AND DISCUSSION

The velocity and temperature gradient at the interface are presented in Tables 1 and 2 for Γ=1 (buoyancy force is unfavorable) and Γ=−1 (buoyancy force is favorable). The velocity f′(0) decreases as Pr increases for Γ=1 and increases with Pr for Γ=−1, while the temperature gradient θ′(0) increases with Pr in both cases. With different values of Marangoni mixed convection parameter λ, the velocity and temperature gradient at the interface increase for Γ=1 and decrease for Γ=−1.

Table 1 Comparison of ′(0)f and ′(0)θ− for different values of Pr and λ with 1Γ=, 1r=, and 1/5k=

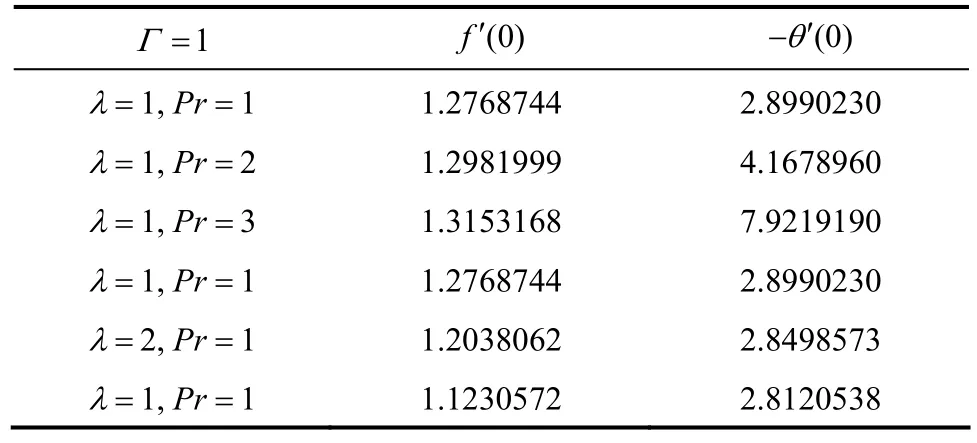
Table 2 Comparison of ′(0)f and ′(0)θ− for different values of Pr and λ with Γ=−1, r=1, and k=1/5

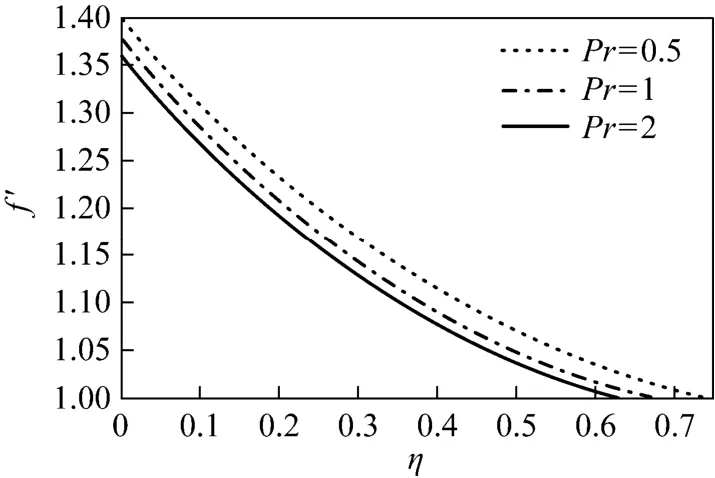
Figure 2 Effect of Pr on velocity profiles for Γ=1 and λ=1

Figure 4 Effect of Pr on velocity profiles for Γ=−1 and λ=1

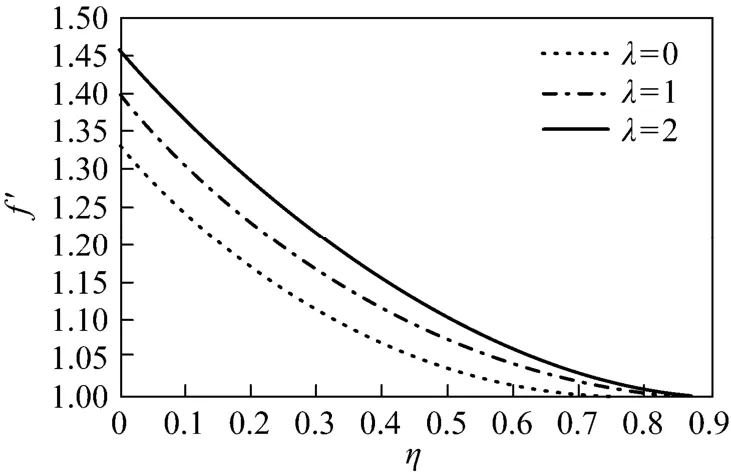
Figure 6 Effect of λ on velocity profiles for Γ=1 and Pr=0.5

To provide more details, the approximate solutions for velocity ()fη′ and temperature ()θη are presented in Figs. 2-9. Figs. 2-5 show the velocity and temperature profiles for 1λ= and some values of Pr. For 1Γ=− (buoyancy force is favorable), both velocity and temperature decrease as Pr increases; for Γ=−1 (favorable case), the velocity increases while the temperature decrease as Pr increases. Figs. 6-9 present the velocity and temperature profiles for fixed Pr and several values of λ. Figs. 6 and 8 show that as the Marangoni mixed convection parameter λ increases, the velocity increases for Γ=1 but decreases for Γ=−1. Figs. 7 and 9 show that the temperature decreases as λ increases for the two cases. Thus λ has a substantial effect on the flow and heat transfer.

5 CONCLUSIONS

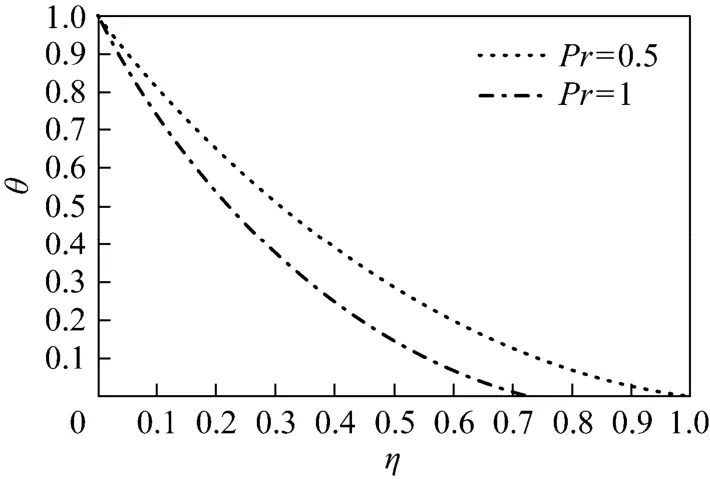
Figure 3 Effect of Pr on temperature profiles for Γ=1 and λ=1

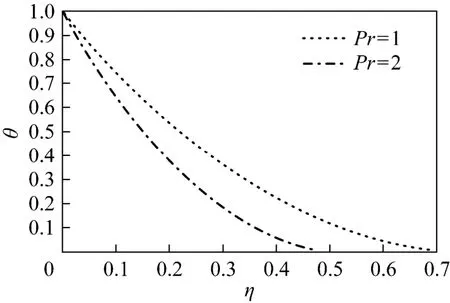
Figure 5 Effect of Pr on temperature profiles for Γ=−1 and λ=1

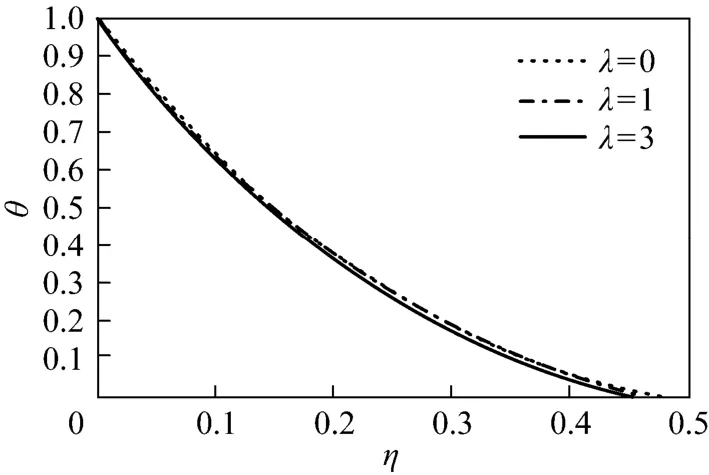
Figure 7 Effect of λ on temperature profiles for Γ=1 and Pr=2

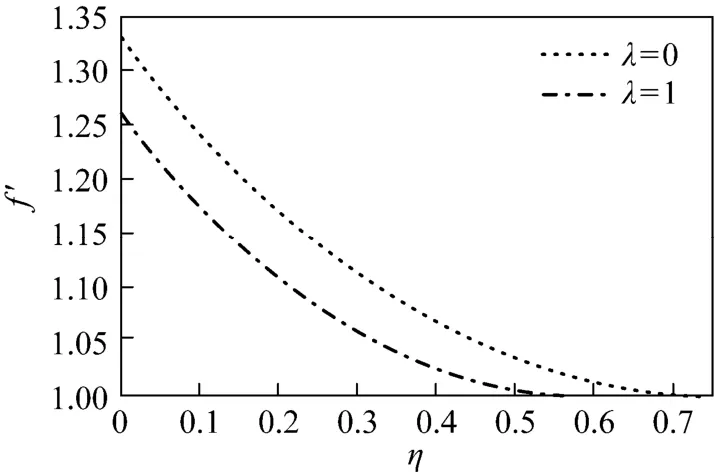
Figure 8 Effect of λ on velocity profiles for Γ=−1 and Pr=0.5

The Marangoni convection boundary layer with gravity and external pressure is studied. The interface curvature is not considered. The approximate analytical solutions for similarity equations are obtained by an efficient transformation, asymptotic expansion and Padé approximant technique. It is concluded that both Marangoni mixed convection parameter λ and Prandtl number Pr have substantial effects on the flow and heat transfer characteristics. The effects of parameters on transfer characteristics are revealed.

NOMENCLATURE

g gravitational acceleration, m·s−2

L extension of relevant surface, m

Pr Prandtl number

Re Reynolds number

T temperature, K

ΔT positive temperature increment along the interface, K

u χ component of velocity, m·s−1

ue(χ) velocity outside boundary layer, m·s−1

v y component of velocity, m·s−1

χ Cartesian coordinate along the interface S, m

y Cartesian coordinates normal to the interface S, m

β thermal diffusion coefficient, m2·s−1

ε small parameter

η similarity variable

θ similarity variable of temperature

μ dynamic viscosity, N·s·m−2

σ surface tension, N·m−1

Ψ stream function, Ω−1·m−1

REFERENCES

1 Zheng, L.C., Chen, X.H., Zhang, X.X., He, J.C., “An approximately analytical solution for the Marangoni convection in an In-Ga-Sb system”, Chinese. Phys. Lett., 21, 1983-1985 (2004).

2 Chen, C.H., “Marangoni effects on forced convection of power-law liquids in a thin film over a stretching surface”, Phy. Lett. A., 10, 16908-16914 (2007).

3 Straub, J., “The role of surface tension for two-phase heat and mass transfer in the absence of gravity”, Eχp. Therm. Fluid. Sci., 9, 253-273 (1994).

4 Wang, S. X., Utaka, Y., “An experimental study on the effect of non-condensable gas for solutal Marangoni condensation heat transfer”, Eχp. Heat Transfer, 2, 61-79 (2005).

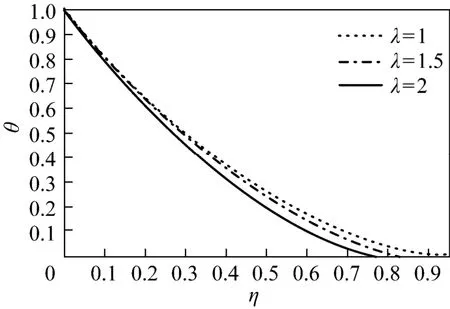
Figure 9 Effect of λ on temperature profiles for Γ=−1 and Pr=0.5

5 Hong, R., Wang, L., Chen, L., Kawaji, M., Ding, J., “Experimental measurement and numerical computation of temperature-gradientdriven Marangoni convection under normal and microgravity conditions”, Comput. Appl. Chem., 23 (5), 385-390 (2006).

6 Arafune, K., Hirata, A., “Interactive solutal and thermal Marangoni convection in a rectangular open boat”, Numer. Heat Trans. Part A., 34, 421-429 (1998).

7 Naimi, M., Hasnaoui, M., Platte, J.K., “Marangoni convection of non-Newtonian power law fluids in a shallow rectangular cavity”, Eng. Computation, 17, 638-668 (2000).

8 Shi, Y., Kerstin, E., “Orientation-dependent hydrodynamic instabilities from chemo-Marangoni cells to large scale interfacial deformations”, Chin. J. Chem. Eng., 15 (5), 748-753 (2007).

9 Magyari, E., Chamkha, A.J., ”Exact analytical results for the thermosolutal MHD Marangoni boundary layers”, Int. J. thermal Sci., 47, 848-857 (2008).

10 Mao, Z., Lu, P., Zhang, G., Yang, C., “Numerical simulation of the Marangoni effect with interphase mass transfer between two planar liquid layers”, Chin. J. Chem. Eng., 16 (2), 161-170 (2008).

11 Hashim, I., Sarma, W., “On oscillatory Marangoni convection in a rotating fluid layer subject to a uniform heat flux from below”, Int. Commun. Heat Mass, 34, 225-230 (2007).

12 Golia, C., Viviani, A., “Non isobaric boundary layers related to Marangoni flows”, Meccanica, 21, 200-204 (1986).

13 Arafune, K., Hirata, A., “Thermal and solutal Marangoni convection in In-Ga-Sb system”, J. Crystal Growth., 197, 811-817 (1999).

14 Slavtchev, S., Miladinova, S., “Thermocapillary flow in a liquid layer at minimum in surface tension”, Acta Mech., 127, 209-224 (1998).

15 Christopher, D.M., Wang, B., “Prandtl number effects for Marangoni convection over a flat surface”, Int. J. Therm. Sci., 40, 564-570 (2001).

16 Al Mudhaf, A., Chamkha, A.J., “Similarity solutions for MHD thermosolutal Marangoni convection over a flat surface in the presence of heat generation or absorption effects”, Heat Mass Transfer., 42, 112-121 (2005).

17 Zhang, Y., Zheng, L.C., Zhang, X.X., “The analytical approximate solution for Marangoni convection in a liquid layer with coupled boundary conditions”, Acta Phys Sin-Ch Ed, 58 (8), 5501-5506 (2009).

18 Zhang, Y., Zheng, L.C., Wang, X.J., Song, G.H., “Analysis of Marangoni convection of non-Newtonian power law fluids with linear temperature distribution”, Therm. Sci., 15 (1), 45-52 (2011).

19 Zhang, Y., Zheng, L.C., Zhang, X.X., “Analysis of MHD thermosolutal Marangoni convection with the heat generation and a first-order chemical reaction”, Chem. Eng. Sci., 69, 449-455 (2012).

20 Sha, Y., Cheng, H., Yu, G., “Marangoni effect in the mass and heat transport processes”, Prog. Chem., 15 (1), 9-17 (2003).

2012-12-08, accepted 2013-04-03.

* Supported by the National Natural Science Foundation of China (21206009), Funding Project for Academic Human Resources Development in Institutions of Higher Learning under the Jurisdiction of Beijing Municipality (PHR201107123), and Program for Doctoral Fund in Beijing University of Civil Engineering and Architecture (101102307).

** To whom correspondence should be addressed. E-mail: zhangbicea@sohu.com