随机布署平面传感器阵列实现色噪声下运动节点跟踪算法*

聂卫科， 朱从光， 房鼎益， 陈晓江，冯大政

(1.西北大学 信息科学与技术学院，陕西 西安 710127；2.中国电子科技集团公司 第三十九研究所，陕西 西安 710065；3.西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071)

随机布署平面传感器阵列实现色噪声下运动节点跟踪算法*

聂卫科1， 朱从光2， 房鼎益1， 陈晓江1，冯大政3

(1.西北大学 信息科学与技术学院，陕西 西安 710127；2.中国电子科技集团公司 第三十九研究所，陕西 西安 710065；3.西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071)

针对色噪声下的空间运动节点跟踪问题，提出一种新的辅助变量子空间跟踪算法。该算法采用秩1更新，构造两个无约束代价函数，求其递归最小二乘解跟踪信号子空间。得到信号子空间后，构造矩阵方程，通过最小二乘解实现空间运动节点的方向跟踪，所得空间二维角度能自动配对。在任意的平面传感器阵列下，所提算法和著名EIV—PAST算法均具有较好的节点跟踪性能，跟踪的信号子空间夹角和信号子空间误差较小，所提算法的正交性能显著优于EIV—PAST算法。

节点定位； 辅助变量； 传感器阵列

0 引 言

很多高分辨的方向估计算法具有优异的参数估计精度[1～3]，但大多是处理空间静止目标。在实际应用中，探测传感器阵列和目标一般存在相对运动，信号入射方向必然会或快或慢地变化，因此,对目标节点的方向信息实时跟踪显得尤为重要。

子空间跟踪方法[4]可以实现运动目标的方向估计，在自适应子空间跟踪算法中，备受关注的是Yang Bin提出投影逼近子空间跟踪[5](PAST) 算法，该算法在将子空间跟踪视为最优化问题求解，并利用投影逼近简化最优化问题，然后使用递归最小二乘法(RLS)对信号子空间的任意基底进行跟踪。由于PAST算法跟踪的子空间误差小、正交性好且性能稳健，此后很多优秀的算法都是在此基础上扩展来的。然而，PAST算法只适用于白噪声,如果确知噪声的相关矩阵，则可以通过白化的方法使色噪声变成白噪声。白化处理复杂度高，且阵元之间噪声相关矩阵通常是未知的，故白化不是一个实用的方法。辅助变量(IV)方法可以解决色噪声环境下的跟踪问题[6]。文献[7]利用IV提出IV—PAST算法。该算法中IV的长度受到限制，而信号子空间估计的准确性是随着辅助变量长度的增加而增加[8,9]，这使得IV—PAST算法的跟踪精度受到制约。文献[7]同时提出EIV—PAST算法，该算法中IV的长度可根据具体情况进行扩展，跟踪性能比IV—PAST算法得到突破性提高。

本文提出一种新的IV子空间跟踪算法，基于秩1更新构造两个无约束代价函数，求其递归最小二乘解得到信号子空间，利用得到的信号子空间构造矩阵方程，通过最小二乘反解空间方向信息，所得二维角度能自动配对。仿真分析中，在任意拓扑布署的平面传感器阵列下，节点方向快慢两种变化情况下，仿真分析了所提算法和著名的EIV—PAST算法跟踪的二维角度，对所跟踪的信号子空间夹角、信号子空间的误差、正交性误差进行了比较。

1 信号模型

考虑P个以窄带信号调制的运动节点，发射信号入射到含M个阵元的任意布署平面传感器阵。设第p个信源的二维方向为(αp,βp)，αp和βp分别为方位和俯仰角。阵元m(m=1,2,…,M)在XOY面上的坐标为(xm,ym)，则阵元m的位置矢量为

lm=[xm,ym,0].

(1)

阵元m接收信源p时的波程差为

Δmp=xmcosαpsinβp+ymsinαpsinβp.

(2)

阵元m接收信源p时的相位差为

amp=exp(-j2πΔmp/λ).

(3)

在第t(t=1,2,…,T)次快拍下所有p个信源在第m个阵元上的总响应为

(4)

式中sp为第p个信源复包络，nm为第m个阵元上与信号独立的色噪声。第t次快拍下阵列接收的数据矢量为

x(t)=[x1(t),x2(t),…,xM(t)]T=As(t)+n(t).

(5)

设ap∈CM×1，其第m个元素为式(3)中amp，则

A=[a1,a2,…,ap],

(6)

s(t)=[s1(t),s2(t),…,sp(t)]T,

(7)

n(t)=[n1(t),n2(t),…,nM(t)]T.

(8)

利用传感器阵元的输出延迟构造辅助变量y(t)

y(t)=[xT(t-f),…,xT(t-f-g+1)]T,

(9)

式中 延迟数f和参数g是设定常数，辅助变量y(t)和观测向量x(t)的相关矩阵定义为C(t)=E[y(t)xH(t)]，常用迭代形式进行运算

C(t)=βC(t-1)+y(t)xH(t),

(10)

式中 0<β<1是遗忘因子。C(t)的奇异值分解为

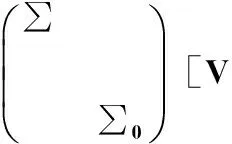
(11)

式中 ∑和∑0分别为大小奇异值组成的对角阵，U和V分别为大奇异值对应的左右奇异主分量。

2 本文算法

根据信号模型中所述的观测向量x(t)、辅助向量y(t)、前一时刻的U(t-1)和V(t-1)估计当前时刻的U(t)和V(t)。采用秩1更新模型

U(t)=U(t-1)+ex(t)gH(t),

(12)

V(t)=V(t-1)+ey(t)hH(t).

(13)

观测向量x(t)在U(t-1)张成的信号子空间的投影为

fx(t)=UH(t-1)x(t).

(14)

辅助向量y(t)在V(t-1)张成的信号空间投影为

fy(t)=VH(t-1)y(t).

(15)

式(12)和式(13)中的g(t)和h(t)为辅助运算引入的变量;ex(t)和ey(t)称为新息，分别定义为

ex(t)=x(t)-U(t-1)fx(t),

(16)

ey(t)=y(t)-V(t-1)fy(t).

(17)

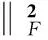
(18)

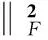
(19)

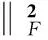
C(t)=βC(t-1)+y(t)xH(t).

(20)

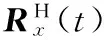
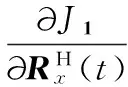
(21)

令导数为0得到Rx(t)=UH(t)CH(t)V(t-1)，本算法每次运算后对U(t)做正交化，所以UH(t-1)U(t-1)=I，而U(t-1)UH(t)≈I，则Rx(t)可写为

Rx(t)=UH(t-1)CH(t)V(t-1).

(22)

这样做的目的是用前一时刻的估计U(t-1)和V(t-1)表示Rx(t)。函数J1对g(t)求导并令导数为0进而求得

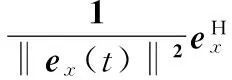
(23)

同理,可得Ry(t)和hH(t)分别为

Ry(t)=VH(t-1)C(t)U(t-1),

(24)

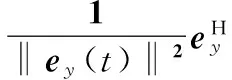
(25)

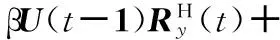
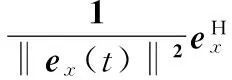
(26)

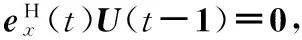
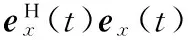
(27)

将式(27)代入式(26)，gH(t)可以简化为

(28)

同理,hH(t)可以简化为

(29)

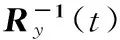
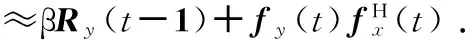
(30)

运用矩阵求逆引理[10]知

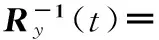
(31)

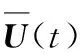
(32)

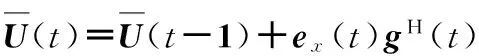
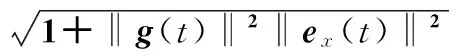
(33)

同理,得到

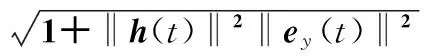
(34)

V(t)的正交化过程同理可得。设W1=[ex(t)+aU(t-1)g(t)+a‖g(t)‖2ex(t)],W2=[ey(t)+bV(t-1)h(t)+b‖h(t)‖2ey(t)],于是得到信号子空间的估计

U(t)=U(t-1)+W1gH(t),

(35)

V(t)=V(t-1)+W2hH(t),

(36)

式(35)所得U(t)即式(5)中A的估计。由于噪声等的影响，估计的导向矢量矩阵固有存在排列和尺度不定性[11,12]，各列排列顺序的不定性并不影响参数估计，而尺度不定可通过求解相邻阵元的相位差消除，设为1的第(m,p)元素，则

(37)

复常数gp为第p列的尺度因子，1第p列第m个阵元与第m+1个阵元的相位差为，设b=则

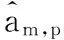
(38)

XYp=Zp.

(39)

其中

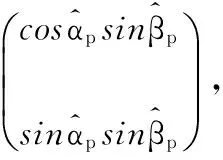
Yp的最小二乘解为

Yp=(XHX)-1XHZp.

(40)

可得到二维方向的估计为

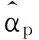
(41)

(42)

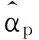
3 仿真实验

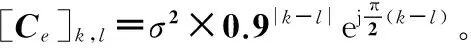
1)慢变化节点的跟踪性能

信噪比为5 dB的慢变化信号，方位角从65°线性变化到85°；俯仰角以[50°+10°sin(2kπ/K)]形式变化，其中,k=1,2,…,K为第k次离散时间点，这里取总时间采样点K=1 000。

由于辅助向量y(t)=[xT(t-f),…,xT(t-f-g+1)]T的建立要求t-f-g+1≥0，所以,在初始一段t<16离散时间内无法实现跟踪。由图1和图2可见，本文算法的对慢变化信号的跟踪效果和EIV—PAST算法基本一致。

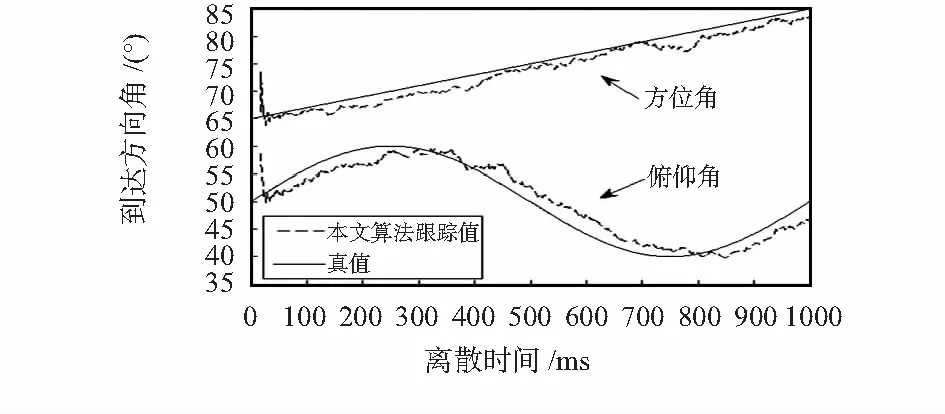
图1 本文算法对慢变化信号的跟踪Fig 1 Slow varying signals tracking by proposed algorithm

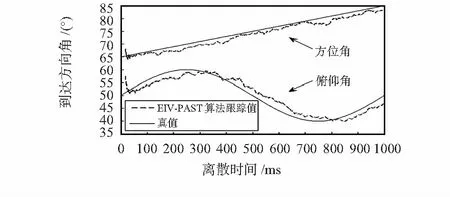
图2 EIV—PAST算法对慢变化信号的跟踪Fig 2 Slow varying signals tracking by EIV—PAST algorithm

图3和图4分别为跟踪的信号子空间的误差和信号子空间夹角。图5为跟踪的信号子空间正交性的误差。由于本文所提算法每步都做了正交化处理，正交性误差相对EIV—PAST算法显著减小。

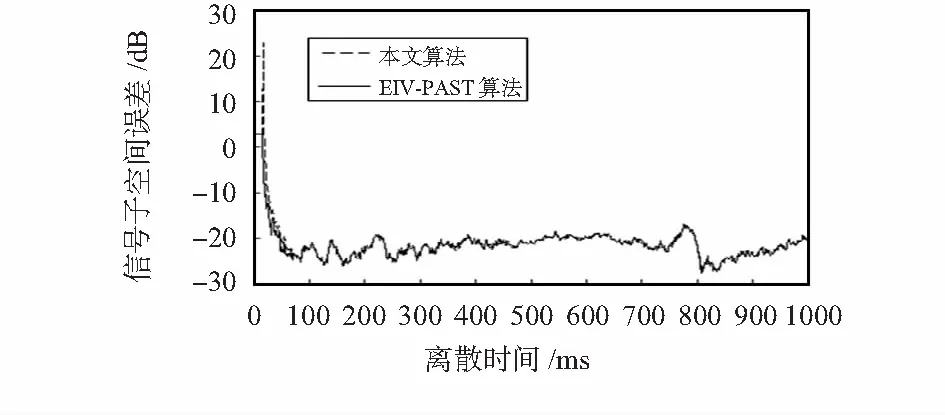
图3 慢变化跟踪的信号子空间误差Fig 3 Subspace error of slow varying tracking signals

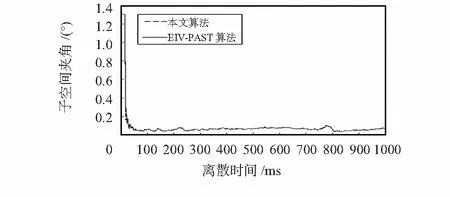
图4 慢变化跟踪的信号子空间夹角Fig 4 Subspace angle of slow varying tracking signals

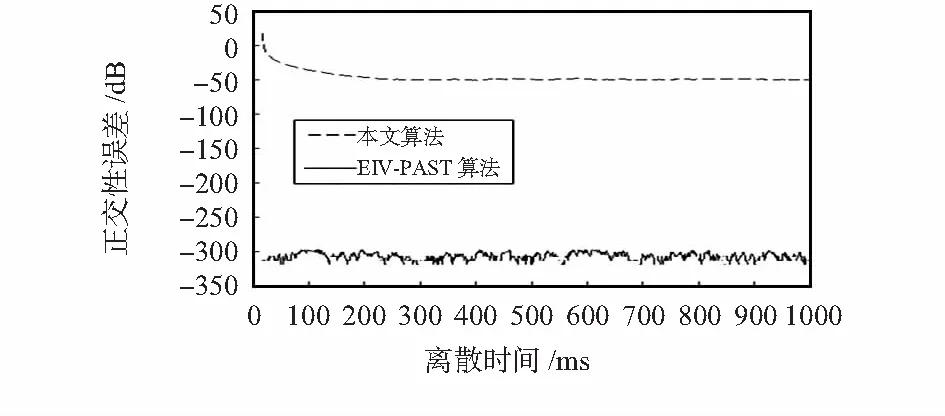
图5 慢变化正交性误差Fig 5 Orthogonal error of slow varying signals

2)快变化节点的跟踪性能

信噪比为5 dB的快变化信号，方位角在500次采样点从75°突变到60°；俯仰角在500次采样点从50°突变到30°。两种算法的跟踪效果见图6和图7所示。由图8、图9、图10可见，在500次采样点处，信号角度发生突变，相应点上的信号子空间误差和信号子空间夹角突然增大，而EIV—PAST算法的正交性误差增大不明显，说明该算法正交性良好。而本文算法即使在突变点，正交性误差仍为-300 dB左右，可以认为是完全正交的。

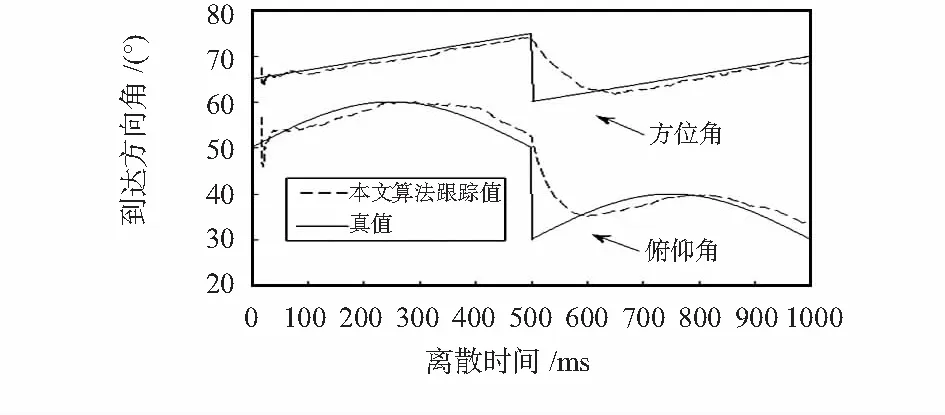
图6 本文算法对快变化信号的跟踪Fig 6 Sudden varying signals tracking by proposed algorithm

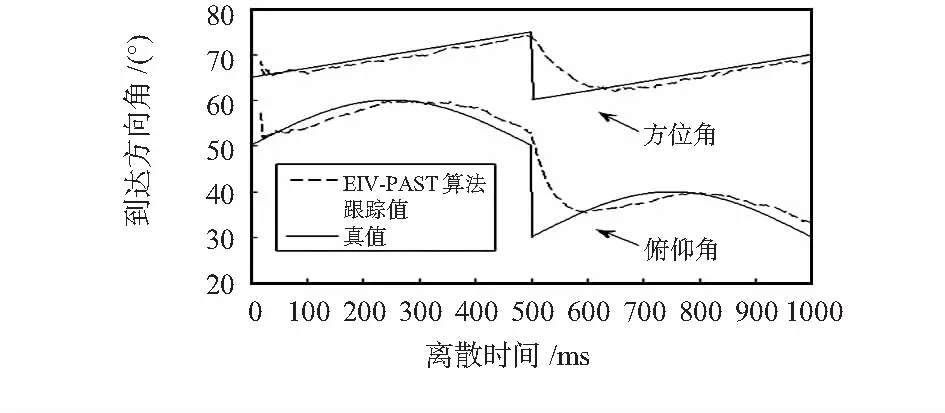
图7 EIV—PAST算法对快变化信号的跟踪Fig 7 Sudden varying signals tracking by EIV—PAST algorithm

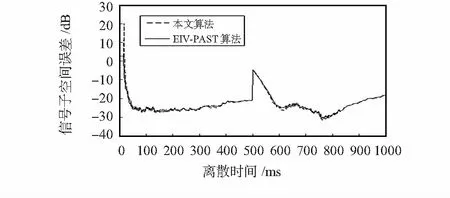
图8 快变化跟踪的信号子空间误差Fig 8 Subspace error of sudden varying tracking signals

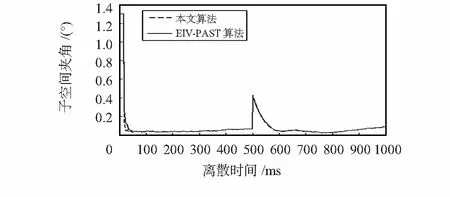
图9 快变化跟踪的信号子空间夹角Fig 9 Subspace angle of sudden varying tracking signals

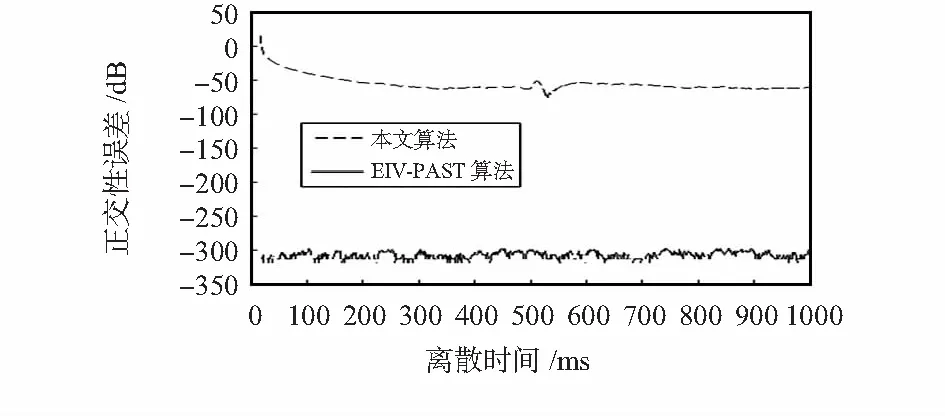
图10 快变化正交性误差Fig 10 Orthogonal error of sudden varying signals

4 结 论

本文提出一种可用于任意平面传感器拓扑结构的空间节点方向跟踪算法。构造两个无约束代价函数，求其递归最小二乘解得到信号子空间，进而求解空间方向。由于采用了辅助变量，使得本文算法可用于色噪声下的方向跟踪。在慢变化和快变化情况下对所提算法的跟踪性能进行了仿真实验，结果表明：所提算法能很好地跟踪空间信号的二维角度，性能和经典的EIV—PAST算法相当,所得到的信号子空间误差和子空间夹角误差较小，尤其是正交性误差显著减小。

[1] Yan K,Wu H,Iyengar S S.Robustness analysis and new hybird algorithm of wideband source localization for acoustic sensor networks[J].IEEE Trans on Wireless Communication,2010,9(6):2033-2043.

[2] 金 勇，程云志，周 柯.基于遗传算法的宽带目标波束空间DOA估计[J].传感器与微系统,2008,27(7):53-55.

[3] Erik G Larsson,Danyo Danev.Accuracy comparison of LS and squared-range LS for source localization[J].IEEE Trans on Signal Processing,2010,58(2):916-923.

[4] Chan S C,Wen Y,Ho K L.A robust PAST algorithm for subspace tracking in impulsive noise[J].IEEE Trans on Signal Processing,2006,54(1):105-116.

[5] Yang Bin.Projection approximation subspace tracking[J].IEEE Trans on Signal Processing,1995,43(1):95-107.

[6] Viberg M,Stoica P,Ottersten B.Array processing in correlated noise fields based on instrumental variables and subspace fit-ting[J].IEEE Trans on Signal Processing,1995,43(5):1187-1199.

[7] Gustafsson T.Instrumental variable sub-space tracking using projection approximation[J].IEEE Trans on Signal Processing,1998,46(3):669-681.

[8] Soderstrom T,Stoica P.System identification[M].London,UK:Prentice-Hall,1999.

[9] Babenko B,Yang M H,Belongie S.Robust object tracking with online multiple instance learing[J].IEEE Trans on Pattern Analysis and Machine Intelligence,2011,33(8):1619-1632.

[10] Horn R A,Johnson C R.Matrix analysis[M].2nd Revised edition.London:Cambridge University Press,2012:5.

[11] Chark F S P,Petraglia M R,Diego B H.A new initialization me-thod for frequency domain blind source seperation algorithm[J].IEEE Signal Processing Letters,2011,18(6):343-346.

[12] Naqvi S M,Miao Y,Chambers J A.A multimodal approach to blind source separation of moving sources[J].IEEE Journal of Selected Topics in Signal Processing,2010,4(5):895-910.

Moving nodes tracking algorithm realized in colored noise by randomly deployed planar sensor array*

NIE Wei-ke1, ZHU Cong-guang2, FANG Ding-yi1, CHEN Xiao-jiang1, FENG Da-zheng3

(1.School of Information Science and Technology,Northwest University,Xi’an 710127,China;2.No.39 Research Institute,China Electronics Technology Group Corporation,Xi’an 710065,China;3.National Key Laboratory of Radar Signal Processing,Xidian University,Xi’an 710071,China)

A new subspace tracking algorithm based on instrumental variable is proposed to estimate the two dimension (2D) localization of aiming at tracking problem of spacial moving nodes in colored noise.By using the rank-one update model,two unconstrained cost functions are established,and signal subspace is derived through the recursive least square solution of the cost functions.Using this derived signal subspace,construct matrix equation and through lease square solution realize direction tracking of spacial moving node,the obtained 2D spacial angle can be paired automatically.In the case of arbitrary planar sensor array,the proposed algorithm and the well known EIV—PAST have good node tracking characteristics,signal subspace angle,signal subspace error are small,the orthonormality performance of proposed algorithm is much better than EIV—PAST algorithms.

node localization; instrumental variable; sensor array

10.13873/J.1000—9787(2014)12—0141—05

2014—08—25

国家自然科学基金资助项目(61373177)；陕西省自然科学基金资助项目(2013JM8008)；陕西省科技厅专项科研计划资助项目(11JK0903)

TP 393

A

1000—9787(2014)12—0141—05

聂卫科(1972-)，男，陕西渭南人，博士，讲师，主要研究领域为无线传感器网络定位与跟踪。