加速度传感器壳体结构参数优化

褚雷阳， 于德润， 刘宝伟， 丁钟凯， 符兴宇

(1.二炮驻哈尔滨地区军事代表室，黑龙江 哈尔滨 150001；2.中国电子科技集团公司 第四十九研究所，黑龙江 哈尔滨 150001；3.哈尔滨工业大学，黑龙江 哈尔滨 150001)

研究与探讨

加速度传感器壳体结构参数优化

褚雷阳1， 于德润1， 刘宝伟2， 丁钟凯2， 符兴宇3

(1.二炮驻哈尔滨地区军事代表室，黑龙江 哈尔滨 150001；2.中国电子科技集团公司 第四十九研究所，黑龙江 哈尔滨 150001；3.哈尔滨工业大学，黑龙江 哈尔滨 150001)

合理的结构参数组合可提高加速度传感器壳体结构的固有频率，保证传感器在振动环境下输出信号稳定。通过建立竖直薄板力学模型，确定影响加速度传感器壳体固有频率的结构因素。基于响应面法思想，利用试验设计的方法，以加速度传感器壳体固有频率为指标，各结构参数为因素，设计二次回归正交旋转组合试验。通过ABAQUS 6.10软件建立各组试验结构参数组合下的分析模型并提取固有频率，最终确定使固有频率维持在较高水平的结构参数组合区间。通过对优化后参数进行验证性试验，表明优化后区间随机结构参数组合下加速度传感器壳体固有频率能够达到10 kHz以上。

加速度传感器； 结构参数； 试验设计； 固有频率

0 引 言

加速度传感器常用于过载、振动和冲击量的测量，广泛应用于卫星导航、武器制导、飞机性能测试等军工项目和民航、汽车、医疗等民用领域的振动冲击测试、机械动态试验、振动校准、信号分析等，特别是在航空航天领域中更有特殊地位[1]。加速度传感器壳体对于传感器芯体和电路部分起承载保护作用，由于加速度传感器在外界动态载荷下工作，当外界激励存在与系统的固有频率相等或相近的频率分量时，系统就会出现谐振现象，导致芯体输出量不准确,甚至结构损坏。由于芯片需要通过合理的工艺安装在传感器壳体内部，所以，芯片感受到外部激励的真正来源是壳体受外界激励而产生的受迫振动。因此,对加速度传感器壳体结构的固有频率进行研究就显得格外重要[2～5]。

加速度传感器壳体结构多为箱体形式，本文对箱体的竖直薄板底端固定模型固有频率进行试验研究，最终确定影响加速度传感器壳体固有频率的结构因素，并采用试验设计(design of experiment,DOE)方法对传感器壳体进行优化分析，以提高传感器结构固有频率。

1 竖直薄板固有频率的影响因素

简化模型如图1。将薄板简化成竖直方向底部固支摆结构，薄板绕支点转动惯量为Jo，摆动过程中薄板偏移平衡位置的角度为θ，薄板振动时两侧等效弹簧刚度系数分别为k，等效刚度作用点距离固定面高为a。

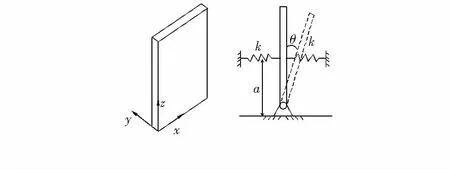
图1 薄板简化模型Fig 1 Simplified model of sheet

利用能量守恒建立方程，即

(1)

确定竖直薄板固有频率wn解析表达式为

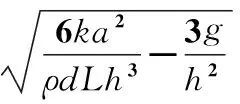
(2)

式中ρ为薄板材料密度，k为薄板等效弹性刚度系数，a为等效弹簧竖直高度，d为薄板厚度，L为薄板纵向长度，h为薄板高度。在以上因素中，薄板材料相对固定，故薄板材料密度可认为不变因素。针对本研究模型，薄板的等效弹性刚度k近似作用在离底面a位置处，k,a的大小受竖直板高度的影响，同时板厚和板长可能会对k,a有影响。

综上，影响竖直薄板底端固定模型固有频率的主要因素共有三个:薄板的厚度d，高度h，长度L。

2 基于响应面法的加速度传感器壳体结构优化

各因素之间对于固有频率存在交互性作用，故运用试验设计的思想，在考察各因素间交互性的同时进行因素优化，以确定保证固有频率在较高水平的结构参数组合[6]。

2.1 影响程度测定方法

对二次回归中各个因素贡献率进行计算， 进而判定各影响因素对响应值的重要性求出各回归系数的方差比F(j),F(jj),F(ij)，令

(3)

求出各个方程对试验指标的贡献率大小，对于第j个因素，其贡献率的计算方法为

(4)

最后通过计算每个因素的贡献率Δj的大小来判别各因素对指标影响的大小[7,8]。

2.2 试验设计

本试验选取d为薄板厚度，L为薄板长度，h为薄板高度作为试验因素，且d=1.3～2.3 mm,L=20～60 mm,h=20～70 mm。

2.3 试验方案与结果

利用Design-Expert数据分析软件根据因素水平编码表设计二次回归中心旋转试验，后利用ABAQUS 6.10有限元仿真分析软件针对于不同结构参数组合提取各组试验模型固有频率。部分试验设计与结果见表1。

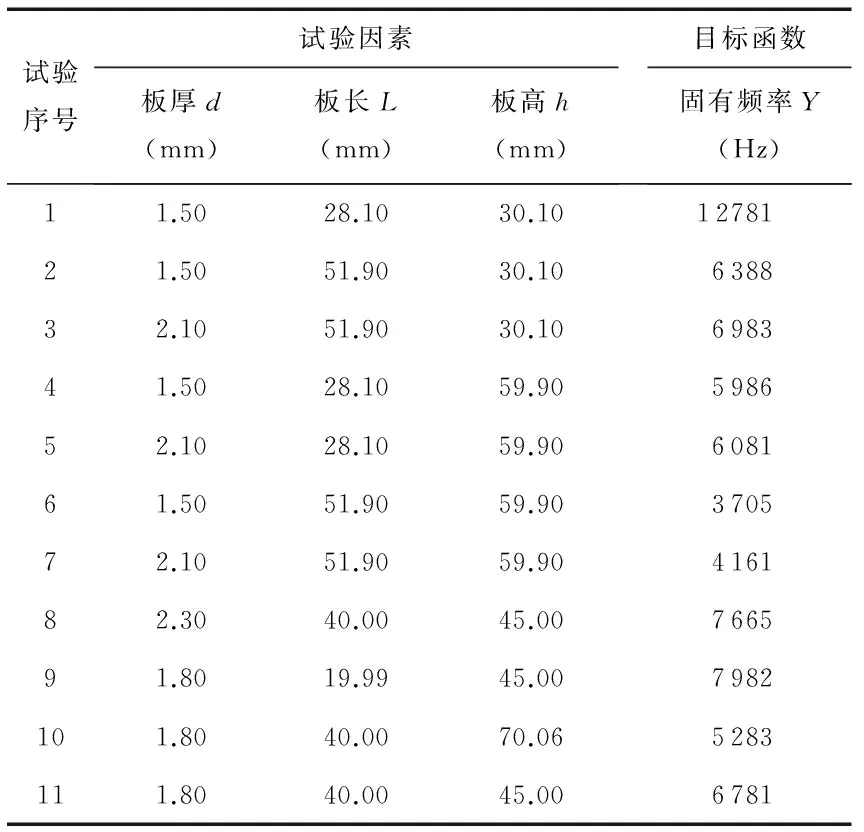
表1 试验设计与结果Tab 1 Design of experimental and results

2.4 各因素对固有频率的影响

固有频率的变化范围为3 705～14 732 Hz，各结构参数组合对模型固有频率影响的回归模型方程如下

Y=-4 351.7+30 446.2d+1 391.1L-765.8h- 13 986.7d2-45.0L2+4.6h2-34.8dL- 55.8dh+7.0Lh+2 558.7d3+0.4L3.

(5)

2.5 回归模型方差分析

通过软件分析与回归模型方差分析发现，在模型中不显著项为：d2，d3，dL将不显著项剔除后，得到回归方程为

Y=12 894.0+3 975.3d+1 328.3L-765.9h- 45.0L2+4.6h2-55.8dh+7.0Lh+ 0.4L3.

(6)

2.6 试验结果分析

在实际设计过程中，考虑产品整体质量、体积等因素要求，需在设计过程中对壳体各个结构因素进行综合性考虑，所以，就需要对影响结构固有频率的因素间交互性作用进行分析并设法确定能够保证固有频率处于较高值的结构参数组合进而指导实际设计。

由图2可知,当高度控制在零水平时，板厚和板长对于固有频率的影响规律：板厚和板长对于固有频率的交互性影响不明显，两个因素均按照各自对于固有频率的影响趋势影响结构的固有频率。观察等高线图发现：在实际设计过程中当用户对于板高有具体要求时，可以通过减小板长并增大板厚的方法提高壳体结构的固有频率。但在设计时也需要综合考虑壳体质量和加工成本、电路板实际安装等问题。

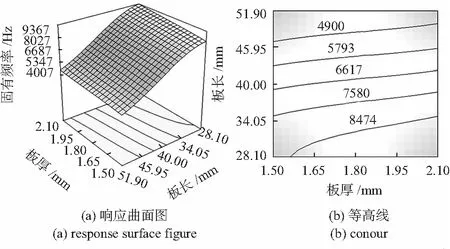
图2 板厚和板长对固有频率的响应曲面图和等高线图Fig 2 Response surface figure and contour of wall thickness and plate length on natural frequency

观察图3发现，当板长为零水平时，壁厚和高度交互作用较差，对于壳体固有频率影响不大，壁厚和高度变化趋势与单因素变化趋势基本相同，当壁厚处于较高水平，高度处于较低水平时，壳体固有频率可以维持在较高值。

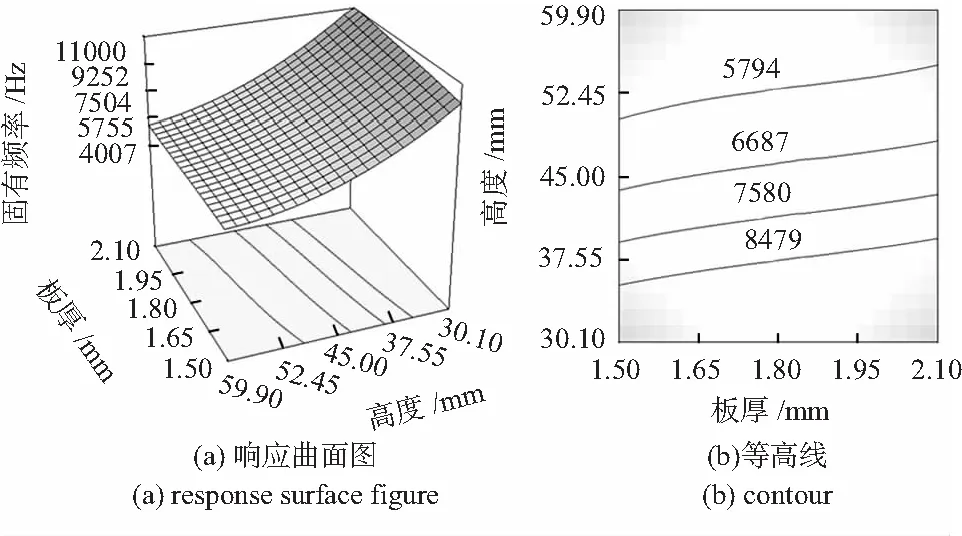
图3 板厚和高度对固有频率的响应曲面图和等高线图Fig 3 Response surface figure and contour of wall thickness and height on natural frequency

图4为当板厚控制在零水平时板厚和高度对固有频率的交互性影响关系图，板长和高度对于固有频率的交互性影响较为明显，当高度和板长均处于低水平时，固有频率为最大值，此时结构抗震性较强。

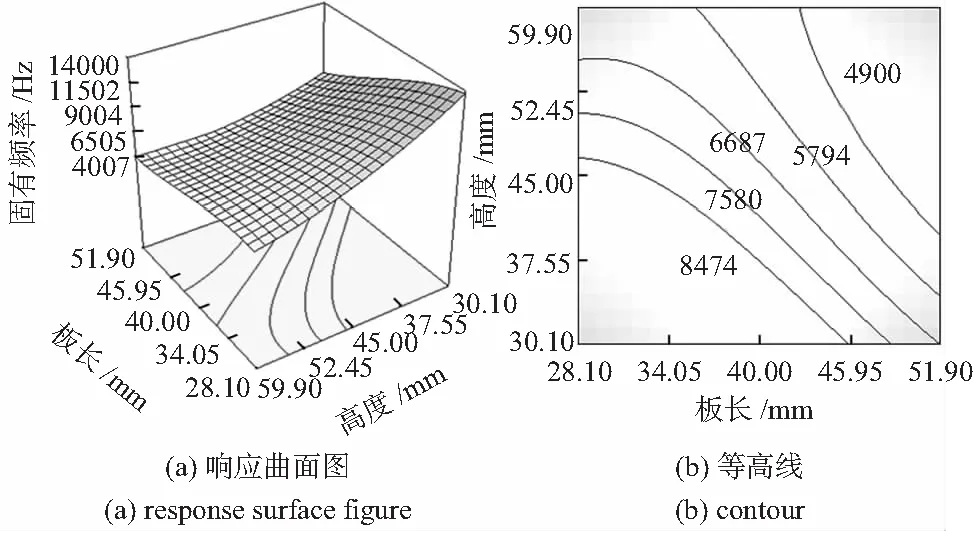
图4 板长和高度对固有频率的响应曲面图和等高线图Fig 4 Response surface figure and contour of plate length and height on natural frequency

2.7 各因素对固有频率的贡献率

根据表2的数据方差分析结果，获得各回归系数检验的方差并将其代入式(3)与式(4)中得到。

计算各因素对固有频率的贡献率分别为

Δ1≈1.141 2，Δ2≈2.518 0，Δ3≈2.887 2,

即高度对壳体固有频率的影响最大，然后为板长、板厚对壳体固有频率贡献最小。明确各因素对壳体固有频率贡献情况对设计师设计过程具有指导意义，可指导设计师了解各结构因素对固有频率的影响关系,并指导设计师通过改变最小的结构参数实现设计要求。

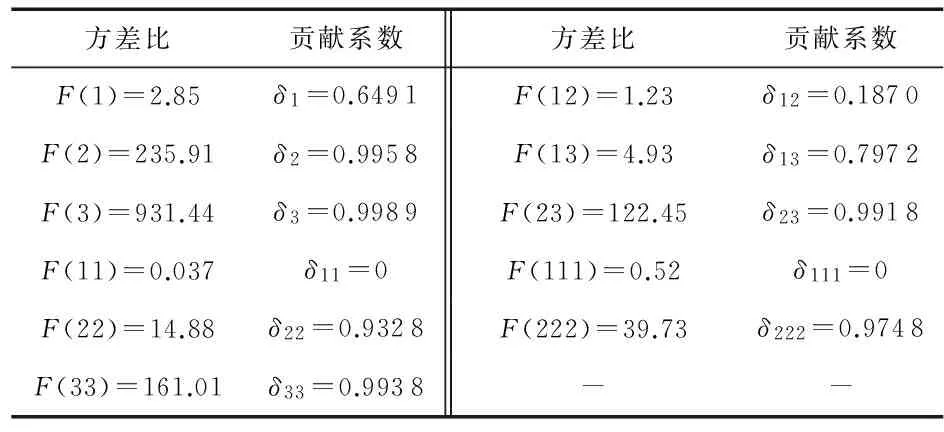
表2 不同方差比下的贡献系数Tab 2 Contribution coefficient in different variance ratio

2.8 参数优化

设计中合理设计参数组合可获得较高一阶固有频率。分别设定每个因素和响应值的目标值以及它们所占的权重，用Design-Expert软件进行择优选择见表3。

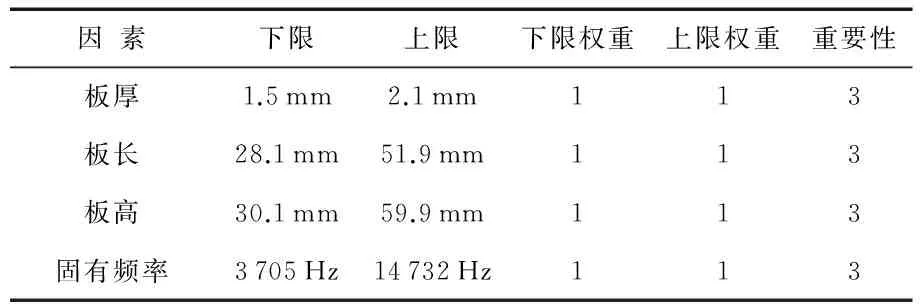
表3 不同因素和响应值的最优标准Tab 3 Optimization criteria for different factors and responses value

在设计过程中，为使结构固有频率尽可能避开实际工作频率，避免壳体因共振所造成结构破坏应尽量提高壳体固有频率。设定优化目标：固有频率10 000～14 000 Hz。得到结构参数优化区域图5。当参数组合满足板长、高度均取较低值时，可保证壳体模型固有频率达10 000 Hz以上，具体区间如图5所示。

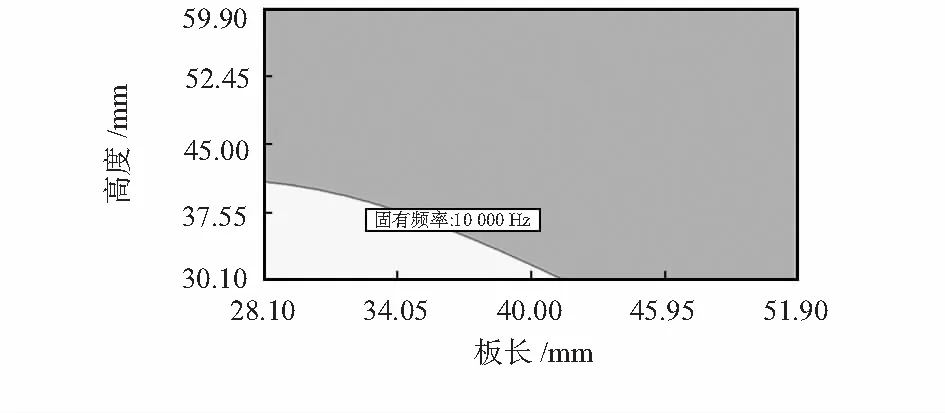
图5 参数优化分析图Fig 5 Optimization analysis diagram of parameters

3 优化参数验证试验

在优化后的区间内随机选取三个试验点，建立壳体模型，并利用ABAQUS 6.10有限元分析软件进行提取固有频率，试验点选取和试验后相应数据见表4。

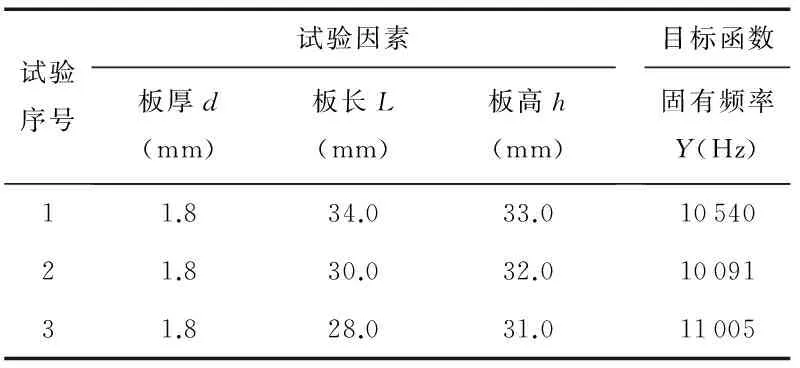
表4 试验设计与结果Tab 4 Design of experiment and results

通过三组验证试验发现，当壳体结构参数组合在优化区域内时，一阶模态固有频率达到10 000 Hz以上，保证壳体具有很好的抗外界振动干扰能力，不易引起结构谐振。同时也说明通过Design-Expert设计优化软件所优化的目标区间具有很好的可靠性，证明了这种设计方法在实际设计过程中的可行性。

4 结 论

1)通过研究，建立了竖直薄板底端固定结构的物理模型，得到薄板模型的固有频率近似解析式,确定了影响薄板模型固有频率的主要因素：薄板长度、薄板高度、薄板厚度；

2)确定了影响壳体固有频率的因素：薄板厚度、薄板长度、薄板高度对于壳体结构固有频率的影响规律，并确定了回归模型方程；

3)确定壳体高度对于壳体的固有频率的影响最大，壳体的板厚对于壳体固有频率的贡献最小,并以固有频率10 000 Hz以上为目标，优化出各参数组合区间。

[1] 吴凌慧，李 涛．加速度传感器壳体结构的动力学特性分析[J]．仪表技术，2011(7)：63-64．

[2] 李 平，石云波.MEMS高gn值加速度传感器固有频率的优化及验证[J]．传感器技术学报，2010，23 (3)：388-389．

[3] 易选强，苑伟政．压阻式微型压力传感器敏感结构设计[J]．西北工业大学学报，2008,26 (6)：782-784．

[4] 汤 帅，许丽萍，温廷敦．基于镜像结构光子晶体的微加速度计设计[J]．传感器与微系统，2014, 33(2)：70-72．

[5] 许本文，焦群英.机械振动与模态分析基础[M].北京：机械工业出版社,1998.

[6] 薛彩军，谭 伟，徐奋前,等．基于响应面模型的结构疲劳寿命优化方法[J]．南京理工大学学报，2011，35(6)：844-846．

[7] 刘 佳，张 宏．基于Design-Expert V7设计的不锈钢激光非熔透搭接焊工艺优化研究[J].机械工程学报,2011(8):52-55.

[8] 袁志发，周静芋.试验设计与分析[M].北京：高等教育出版社,2000.

Shell structural parameter optimization of acceleration sensor

CHU Lei-yang1， YU De-run1， LIU Bao-wei2， DING Zhong-kai2, FU Xing-yu3

(1.The Second Artillery Corps Representative Office in Harbin，Harbin 150001,China;2.The 49th Research Institute，China Electronics Technology Group Corporation，Harbin 150001,China;3.Harbin Institute of Technology， Harbin 150001,China)

Reasonable structural parameter combination can improve natural frequency of shell structure of acceleration sensor, ensure output signal stable in vibration environments.Through building mechanical model for vertical plate to determine structural factors which impact natural frequency of acceleration sensor shell.Based on idea of response surface method,use design of experiment(DOE)methods，use natural frequency of acceleration sensor shell as an index and use each structural parameter as factor to design the quadratic regression orthogonal rotation combination experiment.Structural parameters of each group of test combined analysis model is set up by using ABAQUS 6.10 software and extract natural frequency,finally determine structural parameter combinations interval which makes natural frequency maintain at a higher level.Through confirmatory test on optimized parameters,the results show that natural frequency of acceleration sensor shell after optimizing interval of random structural parameter combinations can reach above 10 kHz.

acceleration sensor; structural parameter; design of experiment(DOE); natural frequency

10.13873/J.1000—9787(2014)12—0013—04

2014—09—05

TP 212

A

1000—9787(2014)12—0013—04

褚雷阳(1974-)，男，黑龙江哈尔滨人，硕士，主要研究方向为地面设备与弹上传感器。