基于有限元法的离子迁移谱电场数值模拟研究

张晶晶，李 明，姜 杰，乔晓林，张冬冬

(1. 哈尔滨工业大学(威海)，山东 威海 264209；2. 中国计量科学研究院，北京 100013)

基于有限元法的离子迁移谱电场数值模拟研究

张晶晶1，李 明2，姜 杰1，乔晓林1，张冬冬1

(1. 哈尔滨工业大学(威海)，山东 威海 264209；2. 中国计量科学研究院，北京 100013)

传统线性离子迁移谱中漂移管电场的均匀性是离子迁移谱性能的主要影响因素之一。本研究利用COMSOL Multiphysics仿真平台，基于有限元法对线性漂移管的内电场进行数学物理建模及数值模拟分析，给出建模方法和均匀电场的标准，研究了电极厚度、绝缘环厚度、漂移管内径以及漂移管外部电场等因素对漂移管内电场的影响，旨在通过模拟结果优化离子迁移谱仪器设计，提高离子迁移谱的性能，为设计者提供参考。

离子迁移谱；电场；有限元；COMSOL Multiphysics

离子迁移谱法(ion mobility spectrometry, IMS)是一种痕量化学物质分析方法，主要通过气态离子的迁移率来鉴别化学物质，达到对物质分析的目的[1]。IMS方法具有可在大气压条件下工作、检测灵敏度高、分析时间短、体积小、重量轻和功耗低等优点，在化学战剂、毒品和爆炸物检测等领域得到了广泛应用，在环境、医学、生物等领域的应用也有了长足的发展[2]。

漂移管是IMS的核心部分，起到分离离子的功能，它的结构设计对IMS的性能有直接的影响。线性漂移管一般由一系列电极环和绝缘环交替排列而成，通过等值电阻连接起来，形成漂移管电场，均匀的电场分布是离子迁移谱仪获得高分辨、高灵敏度信号的保障。因此，通过电场模拟的结果对仪器设计进行指导变得尤为重要。

近年来，通过计算机模拟计算来指导漂移管结构的优化已有报道。Soppart等[3]利用有限差分模拟程序研究了漂移管内电场的分布，指出电极环的厚度与内径之比越小越好，对漂移管的设计有了初步的理论指导。时迎国等[4]利用电场模拟的结果优化设计了IMS仪器的结构。Liu等[5]通过模拟电极环、绝缘环的厚度，外径及形状对电场均匀性的影响优化了仪器结构。杨杰等[6]和Han等[7]利用SIMION软件对传统线性漂移管进行了多物理场模拟。以上研究大多针对自制仪器进行了电场模拟和参数优化，并没有给出全面的几何设计对电场均匀性影响的一般性规律；此外上述工作大多基于有限差分法进行电场求解，虽然该方法相对比较直观，计算速度快，但它难以处理复杂的、不规则的求解域，而有限元法更易实现对偏微分方程的离散，适合处理复杂区域，并能保证计算精度。

COMSOL Multiphysics是一款基于有限元法的高级数值仿真软件，它能高精度的求解偏微分方程(单物理场时)或偏微分方程组(多物理场的情况)，在COMSOL Multiphysics中可根据需要将边界区域的网格剖分加密，因此边界处的物理量计算更精确，进而实现真实物理现象的模拟。目前，COMSOL Multiphysics已在声学[8]、光学[9]、化学反应[10]、地球科学[11]、电磁场[12]等领域有着广泛的应用。Barth等[13-14]和Cumeras等[15-16]利用COMSOL Multiphysics软件对非对称电场漂移管进行了多物理场模拟，而基于COMSOL Multiphysics对线性电场漂移管的模拟研究未见报道。本研究利用COMSOL Multiphysics软件基于有限元法对传统线性电场漂移管进行系统模拟，并总结关键参数对电场均匀性的影响规律，为IMS的设计提供参考。

1 电场数值模拟的基本理论及方法

IMS内电场问题属于静电场问题，可以通过求解泊松(poisson)方程来实现。泊松方程的表达式为：

▽2·φ=-ρ/ε

(1)

式中φ为电势，ρ为自由电荷密度，ε=ε0εr，εr为介质的相对介电常数，ε0为真空介电常数(ε0=8.545·10-12F/m)。

若求解域内没有自由电荷，则泊松方程就简化为拉普拉斯方程：

▽2·φ=0

(2)

为了求解上述方程，还需给定求解区域边界上的物理情况，即需要指定边界条件。本研究利用狄利克雷(dirichlet)边界条件，即给定边界面上各点的电势φ=φ0，在计算机的辅助下求得漂移管内电场的数值解。

COMSOL Multiphysics拥有大量预定义的应用模式，本研究选用静电应用模式。定义相关参数后，建立的几何模型截面示意图示于图1。

图1 漂移管几何模型示意图Fig.1 Schematic diagram of drift tube geometry model

设定电极环、绝缘环的材料分别为不锈钢和聚四氟乙烯，漂移管内外介质为空气，指定各电极环的电势φn(n=1,…,N，N为电极环的个数)。此外，为了观测漂移管电场分布情况，在漂移管外添置一个矩形作为求解域，矩形的4个边界条件设置为“零电荷/对称”。网格剖分方式选用默认的“自由剖分三角形网格”，在此基础上手动控制最大单元和最小单元尺寸。利用其他软件模拟电场时，常因无法精密刻画电极边界形状而使模拟的精度受到影响，而在COMSOL Multiphysics中可以根据需要将边界区域的网格剖分加密，示于图2。因此，边界处的物理量计算更精确，这也是基于有限元方法计算出的电场分布较有限差分法精确的原因之一。

由于此模型求解的是单物理场稳态问题，选用最基本的稳态线性求解器。

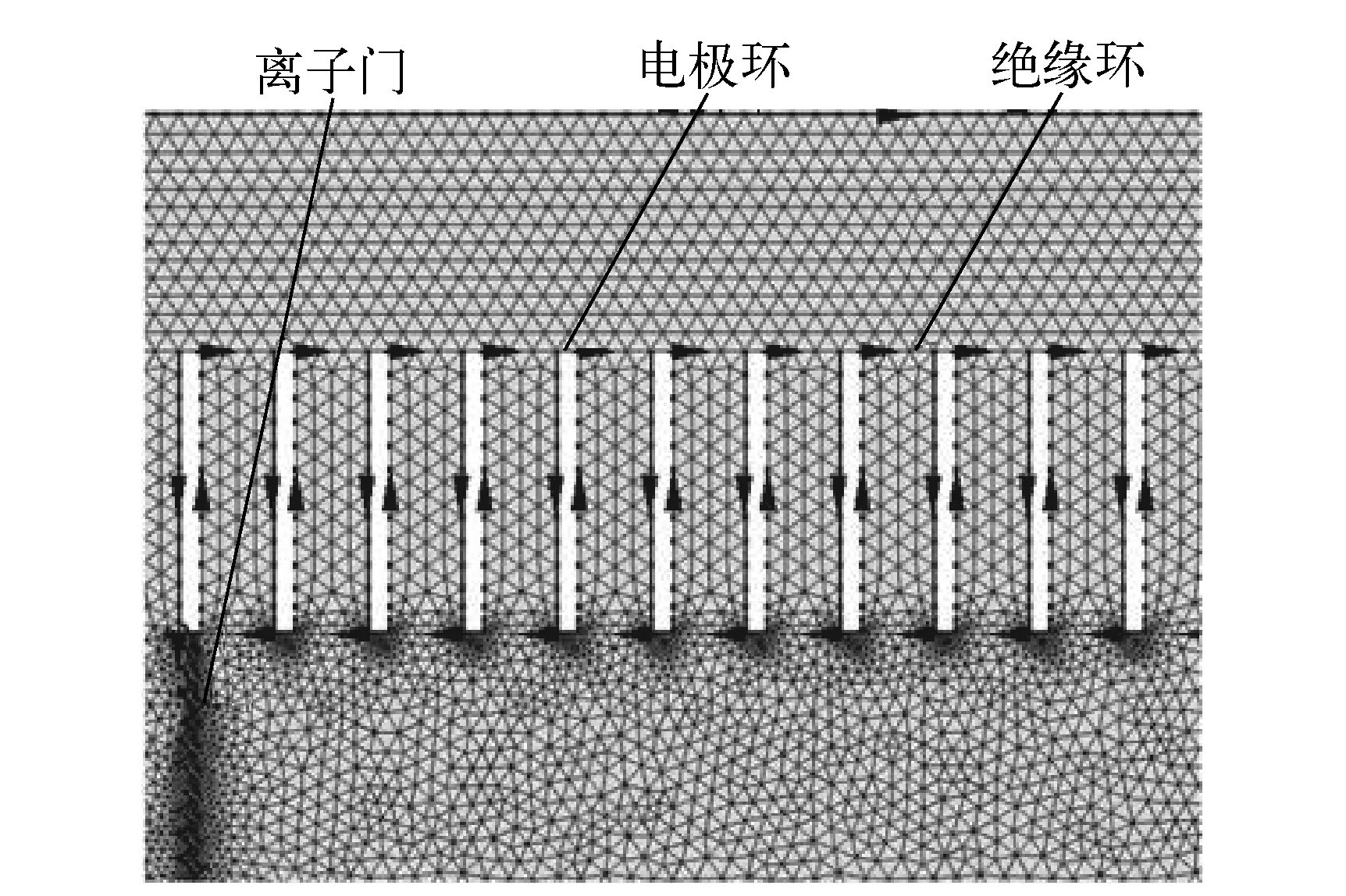
图2 网格剖分局部放大图Fig.2 Partial enlargement drawing of meshing sequence

2 模拟结果

本研究基于COMSOL Multiphysics数值仿真平台分别模拟电极厚度、绝缘环厚度、漂移管内径以及漂移管外部电场等因素对漂移管内部电场的影响。因为反应区的电场分布规律与漂移区的一致，为了简化说明，本工作重点研究漂移区的电场分布情况。如未做特殊说明，下面用到的几何参数列于表1。

2.1 电极厚度对电场分布的影响

模拟的几何模型的坐标设置示于图1，漂移区截面图的水平方向定为X轴，纵向为Y轴，单位均为cm。根据IMS的工作原理，在设计漂移管时尽量使电场在X方向的值趋于一个定值，而在Y方向尽量为零。

表1 漂移管几何模型参数列表

为了直观的表现漂移管的几何设计参数对电场均匀性的影响，在本研究中，人为定义一个衡量电场均匀性的标准，即某区域内的电场强度(以250 V/cm为例)变化的相对偏差在4%内，认为电场在该区域内的分布是均匀的。那么通过数值模拟可以得到漂移管所对应的均匀电场边界值y0，使得在0≤|y|≤y0范围内电场满足下式条件：

|Ey|≤10 V/cm，

240 V/cm≤Ex≤260 V/cm

(3)

其中，Ey为电场强度的纵向分量；Ex为电场强度的水平分量。

电极厚度分别为0.1、1、3 mm时，Ey分布对比图示于图3，易知电极厚度越小，y0值越大，即电场均匀性的范围越大。

图3 不同电极厚度时电场y分量的对比图Fig.3 Comparison chart of the electric field y-component for different thicknesses of electrode

3种条件下，Ex在距轴心线0.83 cm平行线上的分布对比示于图4。由图4可以看出，电极越薄，围绕理想值振荡幅度越小,电场均匀性越好。

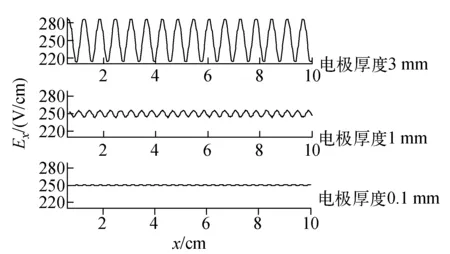
图4 不同电极厚度时电场x分量分布的对比图Fig.4 Comparison chart of the electric field x-component for different thicknesses of electrode

为了量化模拟结果，定义比值η1和η2：

η1=y0/r，η2=S0/S=η12

(4)

其中，r为电极环半径，单位cm，本节r为1 cm；S0为均匀电场的面积，S0=πy02；S为漂移管内腔的横截面积，S=πr2。η1和η2越大，均匀电场所占比例越大。通过数值模拟求出绝缘环厚度为3 mm，电极内径为20 mm时，对应图3所示的3种电极厚度3、1、0.1 mm，η2所占的百分比分别为44.89%、68.89%、92.16%。

数值模拟结果说明，仅从电极厚度对电场分布影响角度考虑，设计漂移管时，在允许的前提下，应尽量减小电极厚度。

2.2 绝缘环厚度对电场分布的影响

绝缘环的厚度也是一个关键参数，本节研究不同绝缘环厚度漂移管内电场的均匀状况。电极厚度为1 mm，电极内径为20 mm，当绝缘环厚度分别为1、3、6 mm时，所对应的η2值分别为77.44%、68.89%、60.84%，可知绝缘环厚度越小，均匀电场的比例越大。

上述3种绝缘环厚度所对应的电场x分量在距轴心线0.83 cm平行线上的分布对比示于图5。由图5可知，随着绝缘环厚度的增加，电场在x方向上的振荡幅度变大，均匀电场的范围变小。所以，在保证有效绝缘效果的前提下，绝缘环的厚度越小越好。

图5 不同绝缘环厚度时电场x分量分布对比图Fig.5 Comparison chart of the electric field x-component for different thicknesses insulating ring

2.3 漂移管内径对电场分布的影响

漂移管内径对内部电场分布有重要影响，在设计时需结合功能、体积综合考虑。通过模拟结果可见：漂移管内径越大，η2值越大，均匀电场的范围越广，结果列于表2。表2中的数据是在固定漂移管壁厚(电极外径与内径差的一半)的前提下得到的。假设壁厚10 mm，此壁厚可保证表2中的结果是在无外部电场干扰下得到的。

如果需要在漂移管内径较小的情况下获得更大的电场均匀区域，可以通过减小电极和绝缘环厚度来实现。漂移管内径1 cm，电极厚度0.1 mm，绝缘环厚度3 mm条件下，η2值较漂移管内径3 cm，电极厚度1 mm，绝缘环厚度3 mm条件下的还大。可见，虽然漂移管内径较小，由于使用了薄电极，同样可以获得较大范围的均匀电场。由表2还可知，当电极厚度、绝缘环厚度和电极内径之比等于1∶1∶10时，计算出的η2值均为60.84%，这说明同比例放大或缩小漂移管，不改变电场分布的均匀性。另外结合2.2结果可以看出，当电极厚度、绝缘环厚度和电极内径之比等于1∶6∶20时，η2值也为60.84%，说明可以通过减小绝缘环厚度来弥补漂移管内径较小时电场分布均匀性变差的现象。

2.4 漂移管外部电场对内部电场的影响

一般离子迁移谱的漂移管外部为接地的金属外壳，需要考虑漂移管壁厚(电极环内外径之差的一半)、绝缘环厚度以及外壳到漂移管的距离等参数，使外壳不会影响到漂移管内部的电场。本研究在数值模拟时将金属外壳与漂移管电极的间距固定在3.0 mm，电极与外壳之间的最大电势差为2 000 V。在无外壳或绝缘环厚度较小时，内电场的均匀性没有受到干扰，示于图6a和6c；而当绝缘环厚度较大，漂移管壁厚较小时，外壳会对漂移管的内电场有较大影响，电场的均匀性变差，示于图6b。漂移管壁厚固定，绝缘环厚度不同时，Ex在距轴心线0.83 cm平行线上的分布对比示于图7。由图7可见,漂移管内电场抗外界干扰能力与漂移管几何设计参数有关。

表2 电极厚度、绝缘环厚度及电极内径之比不同时，η2值的结果对比

注：a. 无外壳；b. 外壳接地；c. 外壳接地(优化几何参数)图6 等势线分布对比图Fig.6 Comparison chart of equipotential line distribution

图7 漂移管壁厚度固定为1 mm，绝缘环厚度不同时Ex分布对比图Fig.7 Comparison chart of the electric field x-component for different thicknesses of insulating ring

当漂移管电极电势低于2 000 V时，漂移管壁厚与绝缘环厚度相等时，即可保证内电场不受外部电场的干扰；否则需要增大漂移管壁厚与绝缘环厚度的比值，才能保证内电场不受干扰。

3 结论

本研究将IMS中的电场问题抽象成数学模型，使用偏微分方程对其进行描述，借助COMSOL Multiphysics软件基于有限元方法求解得到了IMS漂移管中的电场分布，进而分别模拟研究了电极厚度、绝缘环厚度、漂移管内径和漂移管外部电场等因素对漂移管内部电场均匀性的影响。采用量化的方式定义了稳定区域，并且以此为依据总结出了以下规律：

1) 电极越薄，内径越大，绝缘环厚度越小，电场的均匀性越好；

2) 电极环内径较小时，可采用薄电极短间距排列的方式；

3) 同比例放大或缩小漂移管几何尺寸不改变电场分布；

4) 漂移管的接地外壳会对内电场产生影响，为了避免外部电场的干扰，应选择合适的漂移管壁厚和绝缘环厚度。

[1] EICEMAN G A, KARPAS Z. Ion mobility spectrometry[M]. Boca Raton: CRC Press, 2005.

[2] 张东风, 孔德义, 梅 涛, 等. 离子迁移谱仪微型化的现状与进展[J]. 仪器仪表学报, 2006, 27(2): 199-204. ZHANG Dongfeng, KONG Deyi, MEI Tao, et al. Present status and prospect of the miniaturized ion mobility spectrometry [J]. Chinese Journal of Scientific Instrument, 2006, 27(2):199-204 (in Chinese).

[3] SOPPART O, BAUMBACH J I. Comparison of electric fields within drift tubes for ion mobility spectrometry [J]. Measurement Science and Technology, 2000, 11(10): 473-479.

[4] 时迎国,杜明娟. 离子迁移谱仪迁移管中电场均匀性的研究[J]. 科学技术与工程, 2010,10(19): 4 752-4 754. SHI Yingguo, DU Mingjuan. Research of the uniformity of the electric field in ion mobility spectrometer drift tube [J]. Science Technology and Engineering, 2010, 10(19): 4 752-4 754 (in Chinese).

[5] LIU X, LI S L, LI M S. Optimization design of drift tube for ion mobility spectrometer based on simulation of drift electric field [J]. International Journal of Ion Mobility Spectrometry, 2012,15:231-237.

[6] 杨 杰, 曹树亚, 郭成海, 等. 离子迁移(IMS)漂移管的多物理场模拟方法研究[J]. 现代科学仪器, 2011, 6: 41-46. YANG Jie, CAO Shuya, GUO Chenghai, et al. A method of multi-physics simulation for drift tube in ion mobility spectrometer (IMS) [J]. Modern Scientific Instruments, 2011, 6: 41-46 (in Chinese).

[7] HAN F, DU Y, CHENG S, et al. Computational fluid dynamics-monte carlo method for calculation of the ion trajectories and applications in ion mobility spectrometry[J]. International Journal of Mass Spectrometry, 2012, 309: 13-21.

[8] STEPANENKO D A, MINCHENYA V T. Deve- lopment and study of novel non-contact ultrasonic motor based on principle of structural asymmetry [J]. Ultrasonics, 2012, 52(7): 866-872.

[9] XIANGRU W, CAIDONG X, XIA W, et al. New side-pump scheme for large mode area fiber lasers by wrapping polished fibers conjugate caustic removed[J]. Optics Communications, 2010, 283(1): 44-48.

[10] NAVARRETE A, MATO R B, COCERO M J, et al. A predictive approach in modeling and simulation of heat and mass transfer during microwave heating. Application to SFME of essential oil of lavandin super [J]. Chemical Engineering Science, 2012， 68(1): 192-201.

[11] BUTLER S L, SINHA G. Forward modeling of applied geophysics methods using comsol and comparison with analytical and laboratory analog models[J]. Computers & Geosciences, 2012, 42: 168-176.

[12] JALAAL M, SOLEIMANI S, DOMAIRRY G, et al. Numerical simulation of electric field in complex geometries for different electrode arrangements using meshless local MQ-DQ method[J]. Journal of Electrostatics, 2011, 69(3): 168-175.

[13] BARTH S, BAETHER W, ZIMMERMANN S. System design and optimization of a miniaturized ion mobility spectrometer using finite-element analysis [J]. IEEE Sensors Journal, 2009, 9(4): 377-382.

[14] BARTH S, BAETHER W, ZIMMERMANN S. Concept of a miniaturized ion mobility spectrometer and a numerical model for fast system design and optimization[C]. Proceedings of IEEE Sensors， 2007:79-82.

[15] CUMERAS R, GRACIA I, FIGUERAS E, et al. Finite-element analysis of a miniaturized ion mobility spectrometer for security applications [J]. Sensors and Actuators B: Chemical, 2012, 170: 13-20.

[16] CUMERAS R, GR'ACIA I, IVANOV P, et al. Comsol simulation of acetone ions in planar ion mobility spectrometer[C]. Proceedings of the 2009 Spanish Conference on Electron Devices. Santiago de Compostela, Spain, 2009:323-326.

Numerical Simulation of Electric Field for Ion Mobility Spectrometer Based on Finite Element Method

ZHANG Jing-jing1, LI Ming2, JIANG Jie1, QIAO Xiao-lin1, ZHANG Dong-dong1

(1.SchoolofInformationandElectricalEngineering,HarbinInstituteofTechnologyatWeihai,Weihai264209,China;2.ChemicalMetrology&AnalyticalScienceDivision,NationalInstituteofMetrology,Beijing100013,China)

The homogeneity of electric field in the traditional drift tube is very critical to the performance of ion mobility spectrometry. In this study, numerical simulation of electric field in traditional drift tube was conducted by means of COMSOL Multiphysics software with finite element method. Additionally, modeling method and homogeneity standard for electric field were also presented. The influences of some important factors such as thickness of electrode and insulating ring, inner diameter of drift tube as well as metal enclosure of drift tube, on the homogeneity of electric field were researched. On the basis of the research, some useful laws were concluded. This paper is aimed at optimizing instrument design through the numerical simulation results, which can help designers to improve the performance of ion mobility spectrometry. Compared with the traditional research methods through experimental structure design, the simulation results can help shorten the instrument development cycles and save development costs.

ion mobility spectrometry; electrical field; COMSOL multiphysics； finite element method

2013-05-08；

2013-06-21

国家自然科学基金(21205023)；山东省自然科学基金(ZR2010BQ011)资助

张晶晶(1983～)，女(汉族)，河北献县人，博士研究生，信息与通信工程专业。E-mail: summer2002198320@163.com

姜 杰(1978～)，男(汉族)，吉林四平人，副教授，从事分析仪器的开发与应用研究。E-mail: hitjiangjie@gmail.com

时间：2014-01-23； 网络出版地址：http://www.cnki.net/kcms/doi/10.7538/zpxb.youxian.2014.0002.html

O 657.63

A

1004-2997(2014)03-0232-06

10.7538/zpxb.youxian.2014.0002