3 000吨级海上巡视船耐波性分析
2014-07-18巍蒋如宏黄嫒翔
刘 巍蒋如宏黄嫒翔
(1.上海交通大学 上海200030 ;2.中国船舶及海洋工程设计研究院 上海 200011)
3 000吨级海上巡视船耐波性分析
刘 巍1,2蒋如宏1黄嫒翔2
(1.上海交通大学 上海200030 ;2.中国船舶及海洋工程设计研究院 上海 200011)
以3 000吨级巡视船为研究对象,运用三维水动力理论对其耐波性能进行了数值计算。文中除了给出零航速时船体垂荡、横摇、纵摇与参考点垂向运动的传递函数(RAO),还进一步进行短期预报,给出航速为0 kn、13 kn、15 kn与18 kn时船体横摇、垂荡、纵摇与参考点垂向加速度的有义值,并与模型试验结果进行对比分析。结果表明:水动力预报值与模型实验值的趋势基本一致。
耐波性能;巡视船;水动力分析;模型试验
引 言
海上巡视船可在海上连续巡航、全天候执法,具备正当防卫能力和航速较高的技术特点,从执行任务的性质和可配备武器的特点看,应归属为准军用船型。
我国海上巡视船的巡航范围主要包括黄海、渤海、东海和南海等海域。这些海域全年出现恶劣海况的概率较高,这对执行任务的巡视船的耐波性提出了较高要求。如果船舶的耐波性不佳,轻则影响巡航任务的顺利执行,重则会影响船舶的航行安全,因此该类船舶的耐波性能设计尤为重要。
1 基本计算原理
1.1 水动力分析
本文水动力分析将采用法国船级社开发的HydroSTAR软件[1-3],它基于三维绕辐射势流理论的计算程序,并综合考虑一阶和二阶问题。在数值分析中,一阶问题采用基于Kelvin源势法,二阶问题采用Molin法。流场的求解则基于频域方法进行。
规则波的定义为:
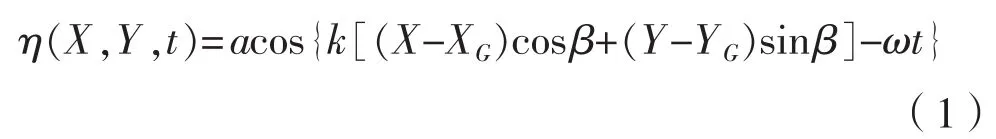
参考点取重心处时,上式可表达为:
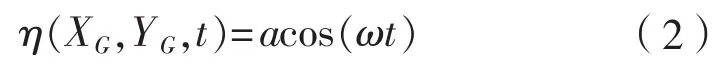
船体在波浪作用下的运动响应可以表达为:

1.2 谱分析
前文介绍的计算方法仅限于规则波中(即获得船体运动的传递函数),而实际海况是不规则且随机的,谱分析可给出特定不规则海况下船体的响应。船体在波浪作用下的响应谱矩可表达为:

式中:为谱密度函数,本文采用ITTC双参数谱[4]。
船体在不规则波中的统计预报一般采用短期预报方法。短期指在某海况下的一段时间(一般为3小时。在此期间,假定船体的装载、航速、浪向以及海况条件均不变化。大量的实践表明,船体运动幅值的短期响应服从Rayleigh分布。该分布只有方差一个参数,即

进而可得到船体运动短期预报的各种统计值,包括均值和有义值等。其中单幅均值:单幅有义值:
2 水动力计算与结果分析
2.1 计算模型
目标船型的主要参数如表1所示。

表1 目标船型主要参数
水动力计算模型包含湿表面模型与质量模型。湿表面模型表征船体在水下的部分,而质量模型表征船体质量在船体的分布情况。由于本文仅研究船体的运动特性,质量模型可以简化,仅考虑质量的大小、质心位置与相关的质量惯性半径。本船横摇惯性半径取0.38B[4],水动力湿表面采用HydroStar的HSMSH模块生成,模型见图1。

图1 湿表面模型
入射波角频率范围为0.05 ~ 2.0 rad / s,取53个频率点;浪向为0°~360°(浪向为船体与波浪的夹角),间隔为15°;此外,还需要定义入射海况和水深等参数。横摇运动临界阻尼系数取5%。
2.2 运动响应传递函数
为了便于结果分析,本文仅给出0°~180°(间隔为30°)的传递函数分析结果。
下页图2-图4给出零航速时船体重心处垂荡幅值、横摇幅值与纵摇幅值的响应传递函数,图5给出船体第19站垂向加速度的响应传递函数。

图2 垂荡幅值响应传递函数
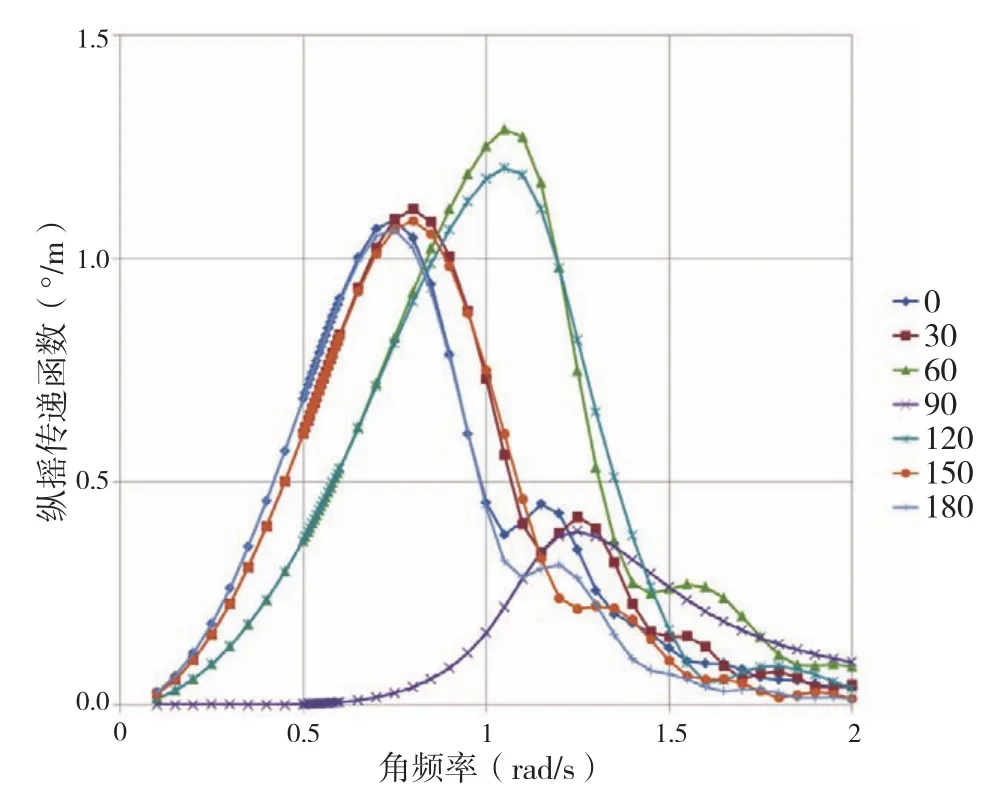
图4 纵摇幅值响应传递函数

图5 第19站垂向加速度的响应传递函数

图3 横摇幅值响应传递函数
由此可见:
① 当波浪圆频率趋向于0 rad / s(即波长趋向无限大时),此时船体的位置可以看成位于波峰或者波谷,那么船体的垂荡幅值为1 m,横摇幅值和纵摇幅值趋向于0°,参考点的垂向加速度趋向于0 m/s2。
② 当波浪的圆频率趋向于2 rad / s(即波长趋向约15 m时),此时波长小于2倍船宽,波浪不具备使船体产生很大横摇的扰动力矩,因此船体横摇幅值很小;波长与船长的比值小于0.2,垂荡幅值、纵摇幅值和参考点的垂向加速度都非常缓和;如果波浪的圆频率继续增大,波长继续变小,那么以上参数均趋于0。
③ 当波浪圆频率在某个范围内时,以上参数均出现峰值区域(如横摇),其峰值对应的波浪圆频率在0.6 ~ 0.7 rad / s,软件计算出的横摇固有周期为9.77 s,固有周期与波浪周期接近,产生共振。
由计算结果可以得出:
① 浪向为90°,波浪的固有频率在0.85 ~1.2 rad / s时,垂荡幅值较大,最大值为1.20 °/m,对应的频率为1.1 rad / s,浪向为90°。
② 浪向为60°~120°,波浪的固有频率在0.58 ~0.7 rad / s时,横摇幅值较大。最大值为16.67 °/m,对应的频率为0.65 rad / s,浪向为60°。
③ 浪向为90°,纵摇幅值较小。其余浪向在特定的频率段均有较大的响应值,且各浪向的最大响应值接近。最大值为2.58 °/m,对应的频率为1.05 rad / s,浪向为60°。
④ 浪向为60°~120°,波浪的固有频率在1.0 ~1.3 rad / s时,第19站垂向加速度的幅值较大。最大值为2.71 m/s2/m,对应的频率为1.15 rad / s,浪向为120°。
2.3 短期预报
图6 -图9列出了零航速不同浪向下的横摇有义值、垂荡有义值、纵摇有义值与第19站垂向加速度有义值。
船体横摇有义值在各浪向下的趋势基本是一致的。浪向角为30°时,横摇有义值的变化趋势较为缓和;浪向角大于45°时,横摇有义值的峰值已经较大,其中60°~ 90°浪向下的横摇有义值基本重合。实船海上运行时,尽量把浪向角控制在30°以内,有利于降低船体的横摇运动[5]。
船体垂荡有义值随着浪向角的增大而增大。在所研究的波浪平均跨零周期范围内,浪向为0°与30°时,垂荡有义值与波浪的平均跨零周期基本成线性关系。浪向为90°,平均跨零周期大于5.5 s时,垂荡有义值稳定在峰值区域。
浪向角为0°、30°与60°时,船体纵摇有义值的最大值接近,只不过最大值对应的的波浪周期有些变化。浪向角为90°时,纵摇较小。

图6 零航速不同浪向下的横摇有义值

图8 零航速不同浪向下的纵摇有义值
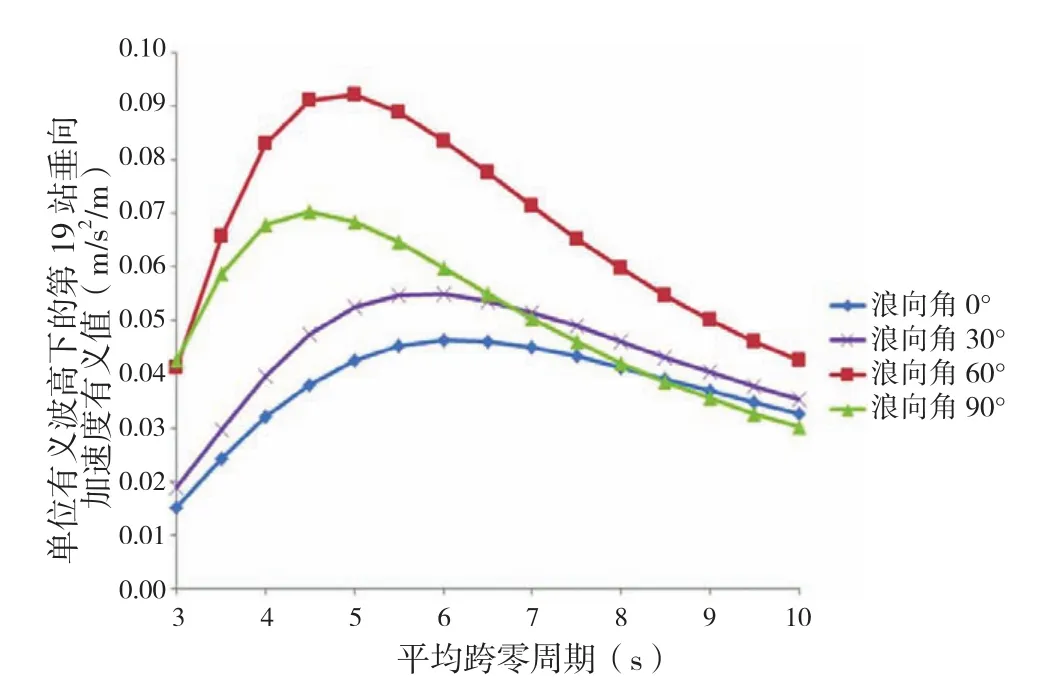
图9 零航速不同浪向下的第19站垂向加速度有义值

图7 零航速不同浪向下的垂荡有义值
第19站的参考点选在中纵剖面上,因此参考点的垂向运动主要是船体垂荡和纵摇的合成作用。浪向角为0°、30°与60°时,参考点垂向加速度有义值随着浪向角的增大而增大。浪向角为90°,波浪的平均跨零周期小于6s时,有义值仅次于60°浪向角时的有义值;波浪平均周期大于6s时,其有义值与0°和30°浪向角时的有义值相当。因此将浪向角控制在30°以内有利于降低参考点的垂向加速度。
图10 -图12给出了迎浪不同航速下的垂荡有义值、纵摇有义值与第19站垂向加速度有义值。

图10 迎浪时各航速下垂荡有义值

图11 迎浪时各航速下纵摇有义值

图12 迎浪时各航速下第19站垂向加速度有义值
波浪的平均跨零周期小于6s时,船体在13 kn、15 kn与18 kn的垂荡有义值基本重合;当周期大于6s时,垂荡有义值的差别开始增大,但是总体趋势仍保持一致,并且18 kn航速时的垂荡有义最大。船体零航速迎浪时的垂荡有义值接近于一条直线,当波浪的平均跨零周期小于4.5 s时,零航速的预报值比其余三个航速下的预报值大;当周期大于4.5 s时,则比其余三个航速下的预报值小。波浪平均跨零周期在7.5 s附近时,零航速预报值与其他三个航速预报值的差值最大;周期继续增大时,差值开始减小。
各航速下的纵摇有义值整体趋势保持一致,但是船体零速纵摇有义值与其他三个航速下的有义值差别稍大。波浪平均跨零周期小于5.5 s时,零速纵摇有义值偏大;当平均跨零周期大于5.5 s时,零速纵摇有义值偏小。
波浪平均跨零周期小于6s,航速为13 kn、15 kn或18 kn时,第19站垂向加速度有义值基本重合;当平均跨零周期大于6s时,加速度有义值的差别开始增大,但是整体趋势仍保持一致。零速垂向加速度有义值与其余三个航速下有义值的差别较大。当波浪的平均跨零周期小于4 s时,零航速下的有义值比其余三个航速下的有义值大;当周期大于4 s时,则比其余三个航速下的有义值小。波浪平均跨零周期在7 s附近时,零航速有义值与其他三个航速有义值的差值最大;周期继续增大时,差值开始减小。
3 数值计算与模型试验结果对比
3.1 模型试验与短期预报
船模试验缩尺比为1∶32,模型的主尺度见表2。

表2 目标船型主要参数
模型试验使用的主要仪器有陀螺仪、三自由度适航仪、浪高仪和加速度计。
试验在本院拖曳水池进行。
(1)模型试验的主要内容
静水中横摇自由衰减试验,记录衰减曲线和横摇周期;零航速横浪规则波试验,测量波浪幅值、波浪周期和横摇幅值;迎浪的规则波试验,测量波浪幅值、波浪周期、纵摇幅值、重心处垂荡幅值、19站处垂向加速度幅值。
对每次试验,取12个不同的波长,分别造出波高约为0.05 m的规则波,记录下各物理量的时间序列并计算出其幅值大小,由此得到各物理量的幅值响应算子。
(2)短期预报
在有义波高为Hs、平均跨零周期为T2的不规则波中,零速横摇的方差可由下积分得到:

横摇的有义值则为二倍的均方差:

由此换算到不规则波的横摇有义值。垂荡、纵摇与垂向加速度有义值的换算与横摇有义值的换算类似。
3.2 短期预报结果对比
目标船型零航速横摇固有周期的预报值为9.77 s,模型试验值为10.75 s,两者相差约10%。
图13为船体重心处零速横摇有义值的结果对比。水动力预报曲线与模型试验曲线的形状和趋势非常吻合,预报结果比模型试验结果稍大些。

图13 数值计算与模型试验的横摇有义值对比
图14为船体迎浪、航速为13 kn的垂荡有义值的结果对比。波浪的平均跨零周期在6s以下时,水动力预报结果与模型试验结果吻合较好;在6s以上时,两者的差距开始增大,水动力预报的结果较大。

图14 数值计算与模型试验的垂荡有义值对比
图15为船体为船体迎浪、航速为13 kn的纵摇有义值的结果对比。可以看出水动力预报值与模型试验值大致趋势保持一致。当波浪平均跨零周期小于8.5 s时,模型试验结果稍大;当周期大于8.5 s时,水动力分析结果稍大。

图15 数值计算与模型试验的纵摇有义值对比
下页图16为船体迎浪、航速为13 kn、第19站垂向加速度有义值的结果对比。在各航速下,水动力预报值与试验值的趋势都是保持一致的。
限于篇幅,目标船型的航速为15 kn与18 kn时模型试验与数值分析结果的对比此处不再赘述。

图16 数值计算与模型试验的第19站垂向加速度有义值对比
4 结 论
本文采用基于三维频域势流理论的水动力软件HydroStar,对某3 000 t海上巡视船的耐波性能进行分析。零航速时,将浪向角控制在30°以内有利于降低船体的横摇、垂荡和参考点的加速度;纵摇仅在横浪时较小,其余浪向下均会出现较大峰值。迎浪航行时,适当降低航速,有利于降低船体垂荡以及参考点的加速度,但对纵摇的影响不太明显。
此外,本文对比了数值分析与模型试验的结果。水动力预报值与模型试验值的趋势基本一致,除了垂荡在部分周期的差值稍大,其余预报值与模型试验值的匹配性均较高。
[1] HSMSH,User’s and Example Manual[M]. Bureau Veritas,2011.
[2] Hydrostar for Experts,User Manual[M] . Bureau Veritas,2011.
[3] Starspec,Hydorstar User Guide[M] . Bureau Veritas,2011.
[4] 盛振邦,刘应中.船舶原理(下)[M].上海:上海交通大学出版社,2004.
[5] 刘宇辰,任毅,蔡新功.三体船横摇运动试验研究[J].船舶,2011(2):20-23.
Seakeeping performance of 3 000 t off shore patrol vessel
LIU Wei1,2JIANG Ru-hong1HUANG Ai-xiang2
(1. Shanghai Jiaotong University, Shanghai 200030, China;2. Marine Design & Research Institute of China, Shanghai 200011, China)
This paper carries out the seakeeping performance of a 3 000 t patrol vessel by the three-dimensional hydrodynamic theory. In addition to the response amplitude operators of heave, roll, pitch and vertical motion of reference points at zero speed, it also show their signifi cant value at 0 kn, 13 kn, 15 kn and 18 kn, and compares with the model test results. It shows that the results of hydrodynamic prediction is in accordance with those of the model tests.
seakeeping performance; patrol vessel; hydrodynamic analysis; model test
U661.32
A
1001-9855(2014)05-0024-07
2013-06-05 ;
2014-08-20
刘 巍(1980-),男,工程师,研究方向:船舶设计与研究工作。
蒋如宏(1972-),男,副教授,研究方向:船舶与海洋结构物设计建造方面的研究。
黄嫒翔(1983-),女,工程师,研究方向:船舶研究与管理工作。
