舵前进流的选择对桨舵系统性能的影响

王 辉李玉胜

（1.上海江南长兴造船有限责任公司 生产运行部 上海201913；2.上海江南长兴造船有限责任公司 精度管理部 上海201913）

舵前进流的选择对桨舵系统性能的影响

王 辉1李玉胜2

（1.上海江南长兴造船有限责任公司 生产运行部 上海201913；2.上海江南长兴造船有限责任公司 精度管理部 上海201913）

为了验证舵前进流的选择对桨-舵系统定常性能的影响，计算了三种舵前进流下的桨-舵系统性能，结果表明，不同进流状态对桨-舵系统性能预报结果十分接近。文中还验证了舵面上诱导速度不取周向平均时对桨-舵定常性能的影响，并对这样计算的诱导速度峰值使用Lagrange插值处理。与试验值比较表明，在计算桨-舵定常性能时，以此方式来计算舵上诱导速度也有效。

桨-舵系统；性能；进流速度；诱导速度

引 言

桨-舵定常水动力性能计算在船舶设计、附体节能装置性能计算和设计中具有重要意义。在计算桨-舵系统性能时，常用的三种方法为［1］：

（1）螺旋桨采用升力面理论，舵采用非线性涡格法；

（2）螺旋桨采用升力面理论，舵采用面元法；

（3）螺旋桨和舵均采用面元法。其中，由于面元法的计算模型能较真实地模拟螺旋桨及其运转情况，因此，在计算桨-舵系统的推进性能和操纵性能时，具有一定优势。本文采用以速度势为基础的面元法计算桨-舵干扰性能，研究了舵前来流速度的选择对计算结果的影响，并就桨对舵面上的诱导速度的不同处理方法进行了分析。

1 桨-舵系统数值计算方法

桨-舵系统计算模型、坐标建立及网格划分如图1。

图1 桨-舵系统计算模型

根据格林第三公式［2］，通过诱导速度考虑桨与舵之间的相互干扰，桨-舵上的速度势方程分别为［3］：

在上式中：Np为一个桨叶和其对应桨毂部分的面元数，Nwp为一个桨叶的尾涡面面元数。Nr、Nwr分别为舵表面及其尾涡面面元数。φ为速度势，为速度势跳跃，其值为在尾缘处上下表面的速度势之差。V0为远方均匀来流速度。n为螺旋桨每秒的转数，rj为第j个面元对应的半径。nj表示第j个面元处的外法线单位向量。δij为Kronecker函数。C、B、W为速度势影响系数，可由蒙瑞诺发展的解析公式求解。上标k（k=0，1，…）表示第k次迭代，，分别表示第k次迭代时舵对桨的诱导速度和桨对舵表面的诱导速度，其中=0，即为螺旋桨敞水状态，为敞水螺旋桨在舵面上产生的诱导速度。由格林第三公式两边求梯度［4-5］可知，

在计算桨-舵干扰时，其计算步骤为：

（1）计算敞水螺旋桨性能及其对舵的诱导速度；

（2）计算处于桨后舵流场中的舵的水动力性能及舵对桨的诱导速度；

（3）将舵的诱导速度计入桨中，重新计算桨的性能、诱导速度；

（4）计算在新的流场下舵的性能、诱导速度。重复步骤（3）、（4），直至桨-舵系统的推力系数与转矩系数收敛。

由压力kutta条件求解的离散方程（1）、（2）得到的结果为速度势，将速度势由柳泽的方法转化为物体表面速度Vtj后，对于螺旋桨前来流，可以认为桨是静止的，无穷远处来流以轴向速度V0，转速n流向螺旋桨，V0=V0ix。因此，根据伯努利方程，每个面元上的压力pj可写为：

将各个面元上的pj计算出来后，即可求得螺旋桨的推力Tp和转矩Qp，螺旋桨的推力系数Ktp和转矩系数Kqp为：

式中：ρ为流体密度，D为螺旋桨直径。

在计算舵上的力时，对于处于桨后的舵，其前端来流有多种处理方式：

（1）以桨对舵前端截面内的轴向平均诱导速度的平均值Vx和无穷远方来流V0之和作为舵的进流，此时［6］：

（2）舵前端沿展向各剖面处的进流不同，分别为各剖面前端的平均诱导速度（包括轴向平均值Vxi、周向平均值Vti和径向平均值Vri）和无穷远方来流速度V0之和。即舵沿展向的各剖面前端的来流为流向舵沿展向的各个剖面。式中：Mr为舵沿展向的面元条数j=1，2，…，Nr，i=1，2，…，Mr。

（3） 直接以远方来流速度V0作为舵前来流。即：

这是由于考虑到桨舵之间的压力，设水流从无穷远场以速度V0流向桨，桨后的压力为p1，桨后水流平均速度为V1，则：

因此，舵上的力可用桨-舵之间的压力和桨后水流平均速度求得：

由以上公式求得舵上受力后，桨-舵系统的性能为：

式中：Tr为舵上沿X轴方向的力。

2 计算结果与分析

文中对MAU4-55桨和NACA0015剖面舵组合体在进速系数为0.55的情况下进行计算，桨和舵的参数如表1［7］。

表1 桨-舵系统参数

在计算时，为了与参考文献［7］试验值对应，定义舵的升力系数：

式中：L为舵升力，与无穷远方来流速度垂直。

桨对舵的诱导速度取周向平均，在进速系数为0.55和0.6时，采用三种不同的舵前进流计算结果如表2、表3，计算值与试验值的比较如下页图2 ～图4所示。

由下页表2与表3可见，这三种舵前进流对于桨-舵系统性能计算并无影响。从图2 ～图4中可以看出，桨-舵系统推力系数和转矩系数与试验值吻合良好。转矩系数随着舵攻角的增大，误差也越大。舵上升力系数的计算值在攻角小于25°时，与试验值吻合良好，这主要是由于随着舵攻角的增大，流体分离现象和边界层厚度对舵性能的影响也越大，这也会影响着桨-舵系统推力和转矩的计算。

诱导速度采用周向平均计算时，舵面上的水流速度是稳定的。实际上，螺旋桨处于不同的位置时，

舵上的诱导速度也会有变化；而且由于存在桨后漩涡，因此桨后诱导速度也不稳定。当舵面上的诱导速度不采用周向平均，而直接取螺旋桨当前位置对舵上每一点的诱导速度值，桨-舵系统性能的计算结果见图5 ～图7中的计算值2；舵角为0°时，舵上的诱导速度见图8 ～图10中计算值2。

表2 J =0.55时不同舵前来流的桨-舵系统性能

表3 J =0.6不同舵前来流的桨-舵系统性能

图2 桨-舵系统推力系数计算值

图3 桨-舵系统转矩系数计算值

在计算桨-舵系统的定常水动力性能时，认为桨后流场连续且不随时间而变化，因此，对于桨后流场中速度峰值处点对应的速度，可以用周围平稳点的速度进行Lagrange插值计算的值代替。对舵上的诱导速度峰值处的点使用Lagrange插值处理后，桨-舵系统性能计算结果如图5～图7的计算值3；舵角为0°时舵上的诱导速度如图8～图10的计算值3。图5 ～图10中，计算值1表示舵上诱导速度取周向平均时的计算结果。由于舵角为0°时，舵是轴对称的，因此图8～图10中只画出了1/4Nr个舵面元上的诱导速度，其中舵面元的编号顺序为图1中的由下至上、由左至右、由上表面至下表面。

从图5 ～图7中可以看出，计算值1和计算值3基本一致，计算值2与它们存在着差异。在图7中，计算值2波动明显，这是由于舵上的诱导速度出现了峰值（如图8 ～图10的计算值2），这些峰值的产生是由于桨后漩涡的存在。从图8～图10可以看出，计算值1和计算值3的速度吻合良好。

使用计算值1和计算值3的舵上诱导速度的计算方法计算的桨-舵系统中舵上速度势如图11。从图中可以看出，这两种方法计算的速度势基本一致，但在计算桨-舵定常性能时，使用计算值3的方法可使计算速度提高数倍。

图4 舵上升力系数计算值

图5 三种舵前进流下桨-舵系统推力系数计算结果

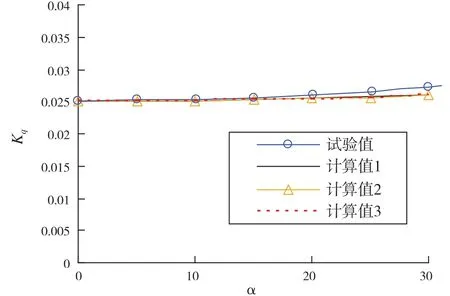
图6 三种舵前进流下桨-舵系统转矩系数

图7 三种舵前进流下舵上升力系数计算结果

图8 舵面上沿X 轴的诱导速度

图9 舵面上沿Y 轴的诱导速度

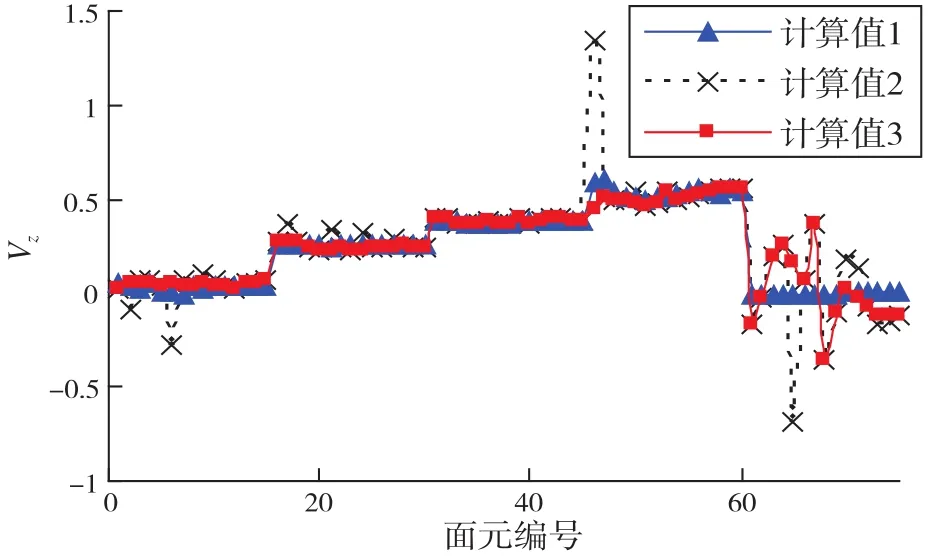
图10 舵面上沿Z 轴的诱导速度

图11 舵面上速度势分布计算结果

3 结 论

文中分别计算了以桨对舵前端截面内的轴向平均诱导速度的平均值和无穷远方来流速度之和作为舵前进流、以桨对舵前端沿舵展向分布的各剖面处的平均诱导速度和无穷远方来流速度之和作为舵各个展向剖面处的进流、以无穷远方来流速度作舵前进流时的桨-舵定常水动力性能。计算结果表明，这三种进流的选择对桨-舵系统性能并无影响。直接使用桨当前位置对舵的诱导速度来计算桨-舵定常性能的计算结果不稳定。文中采用的计算当前位置桨对舵的诱导速度，并对速度的峰值使用周围平稳点速度进行Lagrange插值处理的舵面诱导速度计算方法来计算桨-舵定常性能是有效的，其计算结果与诱导速度采用周向平均时基本一致，而且使用这种舵面诱导速度计算方法的桨-舵定常性能的计算时间较周向平均而言可缩短数倍。

［1］ 王国强,董世汤.船舶螺旋桨理论与应用［M］.哈尔滨：哈尔滨工程大学出版社，2007：380-385.

［2］ 戴遗山,段文洋.船舶在波浪中运动的势流理论［M］.北京：国防工业出版社，2008：1-5.

［3］ ZHANG Jian-hua, WANG Guo-qiang, JIANG Shao-jian. Unsteady Hydrodynamic Performance of Propeller and Rudder System［J］. Journal of Ship Mechanics. 2003,7（3）：48-56.

［4］ 苏玉民，池畑光尚，甲斐寿.船舶螺旋桨尾流场的数值分析［J］.海洋工程，2002，20（3）：44-47.

［5］ 胡建，马骋，黄胜，等.舵对螺旋桨尾流场的影响［J］.华中科技大学学报（自然科学版），2010，38（4）：105-108.

［6］ 苏玉民,黄胜.船舶螺旋桨理论［M］.哈尔滨：哈尔滨工程大学出版社，2003：159-163.

［7］ HASSAN G, PARVIZ G. Computational hydrodynamic analysis of the propeller-rudder and the AZIPOD systems［J］. Ocean Engineering, 2008（35）：117-130.

In fl uence of entrance velocity conditions on propeller-rudder system

WANG Hui1LI Yu-sheng2
(1. Production Executive Department, Shanghai Jiangnan-Changxing Shipbuilding Co.,Ltd., Shanghai 201913, China; 2. Accuracy Control Department, Shanghai Jiangnan-Changxing Shipbuilding Co.,Ltd., Shanghai 201913, China)

Three entrance velocity conditions are considered in the calculation of performance of propellerrudder system performance to verify the influence of entrance velocity on its steady performance. The results show that the system has similar performance with different inflow conditions. This paper also verifies the influence of non-averaged induced velocity on the steady performance of propeller-rudders, and calculates the speed peak value by Lagrange interpolation. In comparison with the experimental results, this calculation method of the induced velocity on the rudder is testified to be effective in the computation of the propellerrudder system steady performance.

propeller-rudder system; performance; entrance velocity; induced velocity

U664.3

A

1001-9855（2014）02-0071-06

2013-09-12；

2013-10-09

王 辉（1985-），男，助理工程师，研究方向：船舶与海洋。李玉胜（1982-），男，助理工程师，研究方向：船舶与海洋。