基于纤维模型的圆钢管混凝土柱的抗震性能

张岚，方亮，魏刚

(湖南农业大学工学院，湖南 长沙 410128)

钢管混凝土结构是一种新型的混和结构形式，在工程实际中正日益得到广泛使用。工作时，空心钢管对核心混凝土起约束作用，使混凝土三向受压，强度得以提高，塑性和延性性能改善，同时，由于核心混凝土的径向压力，使得钢管材料由单向受压变为拉压二向应力状态，拉应力的存在能有效缓解钢管的局部屈曲，能充分发挥钢材的强度性能，这是钢管混凝土结构具有较好抗震性能的重要原因。对其滞回性能进行数值模拟，是圆钢管混凝土柱抗震性能研究的热点领域。国内外学者对圆钢管混凝土结构抗震性能研究主要集中在试验领域，但数值模拟方面的研究工作相对滞后，K. A. S. Susantha等[1]采用大型通用有限元软件ABAQUS的铁木辛柯梁单元数值，模拟了钢管混凝土柱的强度及延性。卢明奇[2]采用空间六面体八节点等参单元，通过设置厚度近似为零的粘结单元，以模拟钢筋与混凝土之间的粘结滑移，对两跨三层的平面钢管框架结构进行了有限元分析。丁阳等[3]分别按照钢管混凝土的统一模量理论和分离模量理论，利用ANSYS 软件对该文献中的钢管混凝土框架模型试验，采用数值方法进行了较为成功的模拟。文献[1–3]中的试验结果和数值模拟结果较为一致，但有限元模型通常采用实体单元，具有计算效率较低和数值计算不稳定、难以收敛的特点。孙修礼等[4]采用纽约州立大学研制的非线性分析程序IDARC，分析了钢梁–钢管混凝土柱和钢筋混凝土梁–钢管混凝土柱2类框架结构的骨架曲线，程序结果和试验结果吻合良好，该程序在确立弯曲–曲率骨架曲线时，也采用了杆件由众多纵向纤维组成的假设，但该程序在模拟三线性滞回骨架模型有下降段的情况时不能收敛。笔者采用非线性梁柱宏观单元数值模拟圆钢管混凝土柱的抗震性能，并进行了参数分析，采用的Mander约束混凝土本构模型和Menegotto– Pinto钢材本构模型，能考虑2种材料的相互作用及钢管材料的包辛格(Bauschinger)效应；分析程序中通过定义非线性弹簧滞回模型来模拟柱的剪切变形的影响，弹簧参数由uniaxialMaterial Hysteretic命令定义，并利用命令section Aggregator将其组装到截面中。采用的纤维模型宏观单元其数值计算稳定，计算精度和计算效率高，收敛快，能有效处理刚度为负的情况下的分析问题[5]。

1 纤维模型非线性梁柱宏观单元

1.1 纤维模型

纤维模型法和有限单元法是钢管混凝土研究中最广泛使用的2种数值模拟方法。纤维模型法将构件的组成理解为数量若干的纵向纤维，这样可将横截面分割成众多的微小截面，如图1。各根纵向纤维可以分别定义不同的材料本构关系，根据材料力学中纵向纤维间无正应力的假设，各纵向纤维处于单向拉伸或压缩的状态，则各纵向纤维可采用单轴本构关系，并能考虑材料的非线性。根据平截面假定，由横截面曲率及轴心正应变，即可得到各纵向纤维的正应变。再根据材料单轴本构关系，能计算出各个微小截面上的内力，通过求和或积分得到横截面的总内力，从而建立起截面的内力和变形的关系。其迭代计算步骤如下。

1) 任设曲率增量Δφ，得到当前曲率为φ=φ+ Δφ。

2) 由轴向力可得截面几何中心处正应变ε0；按式εi=ε0+yiφ，可求出各纵向纤维的正应变εi。

3) 根据材料单轴本构模型，可求出各纵向纤维的正应力，将截面上空间力系向其几何中心简化，可得截面内力及内力偶。

4) 当计算出的截面内力与由形函数插值得到的内力误差在允许范围内时完成迭代计算，否则返回步骤1，直至满足误差要求。

5) 由当前的截面变形–截面内力的广义本构关系，可计算截面柔度。

图1 圆钢管混凝土柱截面纤维划分 Fig.1 Fiber section division of the column

1.2 非线性梁柱单元

非线性梁柱单元有基于刚度法的单元和基于柔度法的单元，前者以杆端位移为基本未知量，后者以杆端力为基本未知量。Mari与Scordelis[6]较早提出了基于刚度法的梁柱单元，该单元通过位移插值函数得到截面的位移和变形，再根据截面内力–截面变形的广义本构关系，建立起截面层面的刚度矩阵，截面层面刚度矩阵沿着杆件长度方向，通过积分即得到非线性梁柱单元的刚度矩阵。该类单元中，由于位移插值函数未能理想地描述端部屈服后曲率的实际分布规律，而且单元层次没有迭代计算，因此收敛速度慢。笔者采用基于柔度法的非线性梁柱单元[7]，该模型以节点力作为基本未知量，且将梁柱沿其长度方向划分成数个积分区间。积分点处的截面内力由力形函数插值决定，(1)式为力插值形函数形式：

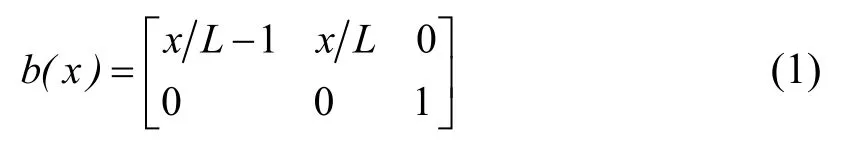
通过截面变形–截面内力的广义本构关系求逆，可得截面柔度矩阵f(x)，由(2)式沿杆长积分可得单元柔度矩阵：

柔度矩阵求逆矩阵得到单元刚度矩阵。截面不平衡力向量可通过截面柔度矩阵f(x)转化为截面残余变形r(x)，沿杆长积分即式(3)得到单元残余变形S：

当插值得到的截面内力与由材料本构模型计算出的截面内力不相等时，便产生了所谓的截面不平衡力，对于这种不平衡力，可通过本构关系转化为截面残余变形，重新进行积分运算。当迭代计算到截面上的不平衡力足够小，达到误差允许要求时，停止单元层面迭代。因为采用了单元层面的迭代计算，所以结构层面的迭代计算其收敛速度明显加快。(2)式的计算可采用Gauss–Lobatto积分法，可将(2)式改写为：

式中：n为沿单元长度方向的积分点数目；ωi为积分点的权数。

2 材料的本构关系

2.1 混凝土应力–应变关系

约束混凝土本构关系的研究，应用较多的有Mander等[8]建立的模型和韩林海等[9]建立的模型。研究结果表明，循环反复加载的情况下，约束混凝土的应力–应变滞回骨架曲线与其单调加载情况下应力–应变曲线基本重合[10–11]，故本研究核心混凝土单轴本构的滞回骨架曲线采用单调加载并经改进后的Mander模型(图3)，该模型考虑了混凝土的拉应力。图3中f′cc和εcc分别表示约束混凝土单向受压时峰值压应力及对应正应变，分别由(6)式、(7)式决定。(5)式为达到峰值应力之前单轴本构关系[8]，图3中f′cu和εcu分别为混凝土极限压应力和极限压应变[12]。fl为混凝土施加给圆钢管的侧向压应力，见图2。

图2 圆钢管混凝土柱截面应力分布 Fig.2 Section stress diagram of circular concrete-filled tube columns

根据力的平衡条件可得到(8)式，其中fsh圆形钢管的切向拉应力，取fsh=0.19fy[13]，D为圆形钢管横截面直径；t为圆形钢管的厚度，数值模拟时取钢管混凝土抗拉强度ft=0.14f′cc，其他参数见文献[8]。

图4表示约束混凝土受压的加卸载准则[11–14]，按照该法则，所有再加载曲线均相交于同一点R， R为水平段B点对应的再加载曲线与O点处曲线切线的交点，由此可求出R点的应力σr和应变εr，其中B点应力为峰值应力的20%。图中Ec为骨架线原点处切线斜率。E20为B点对应的再加载刚度，根据试验测定，或取值为0.1Ec[15]。Er为骨架线上某卸载点与R点连线的斜率。约束混凝土受拉时的加卸载准则参见文献[11]。

图3 改进的Mander 约束混凝土本构模型 Fig.3 Modified Mander-confined concrete constitutive model

图4 约束混凝土受压加卸载准则 Fig.4 Loading and unloading criterion of confined concrete under compression

2.2 钢材的应力–应变关系

为模拟钢材在循环荷载作用下的性能，须考虑钢材同向强化和随动强化以及包辛格(Bauschinger)效应[16]。本研究采用经Filippou等修正的Menegotto－Pinto钢材非线性模型，如图5所示，并可由(9)式～(11)式[14]表示。

其中参数：

图5中，直线AB和直线BC为钢材本构曲线的渐近线，E0和E1分别为渐近线AB和BC的斜率。σr和εr分别为本构曲线上应变转向点，即A和C的应力和应变值，σ0和ε0分别为图5中某一同向本构曲线2渐近线交点的应力(纵坐标)和应变(横坐标)。(9)式中：b为E1与E0的比值；R为与本构曲线的曲率有关的参数，反映了包辛格效应，其值由(12)式决定，其中R0为初始值，与a1和a2一起均由试验确定；ξ 由(13)式决定，而εm为前一加载循环中应变开始反向时的值，ε0为紧邻其前的本构曲线2渐进线交点的应变值，σy和εy为钢材屈服应力和屈服应变。新的加载循环内(σr，εr)和(σ0，ε0)均需更新。

图5 钢滞回本构模型 Fig.5 Steel hysteresis constitutive model

3 圆钢管混凝土柱抗震性能

地震作用具有往复性，结构在地震作用下的反应属于动力学行为，其抗震性能与多项参数有关，通过静力反复加载试验或静力滞回曲线的数值模拟，可以把握这些参数的变化规律。结构的抗震性能与承载力退化、刚度退化、耗能能力等多项指标有关。承载力退化与刚度退化越严重，则结构的抗震性能越差；耗能能力越强，则结构的抗震性能越好。延性大、刚度退化小的结构抗震性能较好。

本研究采用开源有限元程序OpenSEES的非线性梁柱宏观单元，采用TCL脚本语言工具编写非线性分析的计算程序，对圆钢管混凝土悬臂杆件的侧向力(P)–侧向位移(Δ)关系的滞回性能进行数值模拟。

3.1 模型验证

为验证上述单元及材料本构模型的适用性，数值模拟了文献[17]中的试件(CFT4)，其模拟结果参见图6。数值模拟结果与文献[17]中试验结果较为一致。

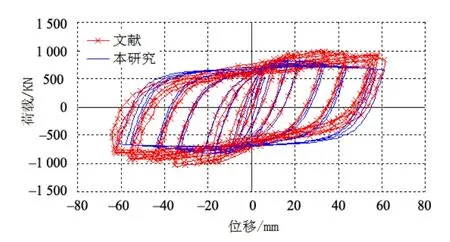
图6 低周循环荷载下柱滞回曲线 Fig.6 Hysteresis curve of column under low cyclic load

3.2 试件设计

为研究各参数对圆钢管混凝土柱的抗震性能的影响，设计了13根框架模型柱试件。模型柱设计依照《钢管混凝土结构设计与施工规程》。模型柱计算简图如图7所示，柱的反弯点取位于柱的跨中。模拟静力反复侧向荷载P及其作用点的侧向位移Δ之间的滞回曲线。各模型柱的具体参数见表1，高度均取l=1 500 mm，钢管外径D=300 mm。定义含钢率为横截面上钢材与混凝土面积的比值，即α=As/Ac。轴压比n=N/N0，其中N为轴向压力。名义压溃荷载N0=fcAc+ fyAs。

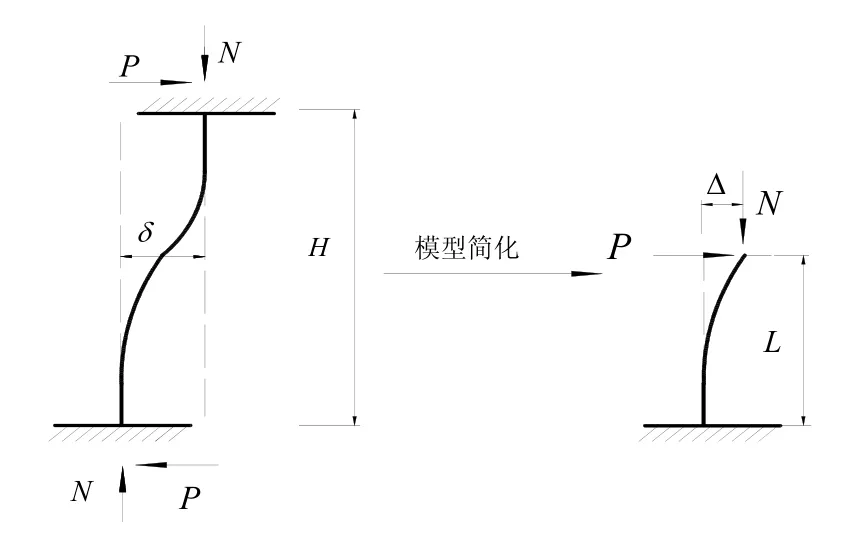
图7 框架柱简化模型 Fig.7 Simplified model of frame column

表1 试件参数 Table 1 Parameter of the tested specimen

3.3 参数分析

图8为本研究模拟的各试件侧向位移Δ与侧向力P滞回关系曲线，图9至图12分别表示不同参数对柱滞回骨架曲线的影响。

图9显示，含钢率对试件骨架曲线影响较大，随着含钢率的提高，柱的承载力、弹性阶段刚度会相应提高。

图10显示，轴压比对试件的骨架曲线影响较大，轴压比较小时，曲线几乎没有下降段；当轴压比较大时，试件会有明显的下降段，极限位移、延性也会随着轴压比的增大而显著降低。故较大的轴压比对试件抗震性能不利。

图11显示，随着混凝土强度提高，试件最大承载力、弹性阶段刚度会相应有所提高，但效果不明显；在强化阶段之后，会随着混凝土强度提高，骨架曲线反而会随之下降较快。故工程实际中混凝土强度不应太高。

图12显示，钢材的强度对试件骨架曲线影响也较大，随着钢材强度的提高，试件的承载力也会随之提高，但对试件弹性刚度几乎没有影响，这主要是钢的弹性模量与其强度几乎没有关系。

图8 侧向力P–侧向位移Δ 滞回曲线 Fig.8 Hysteresis curve between lateral load and lateral displacement

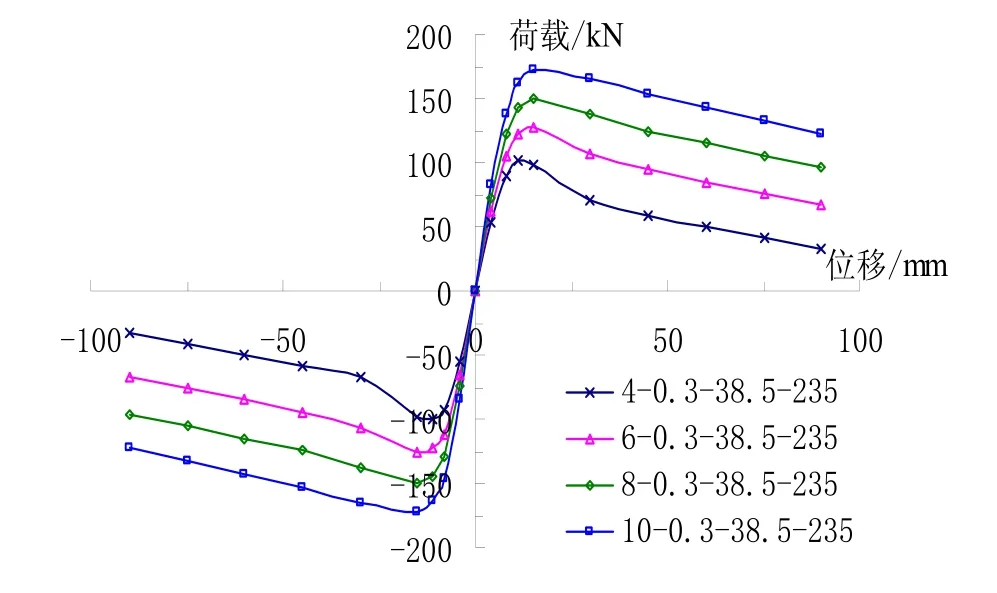
图9 不同含钢率下荷载–位移曲线 Fig.9 Load-displacement curves under different steel ratios

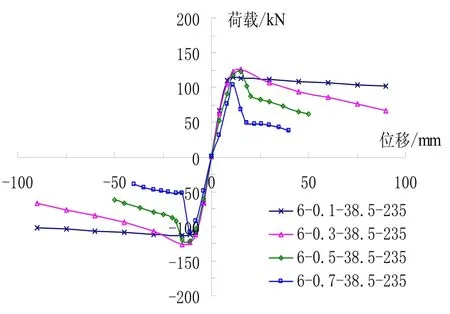
图10 不同轴压比下荷载–位移曲线 Fig.10 Load-displacement curves under different axial compression ratios

图11 不同混凝土强度下荷载–位移曲线 Fig.11 Load-displacement curves under different concrete strengths

图12 不同钢材强度下荷载–位移曲线 Fig.12 Load-displacement curves under different steel strengths

4 结 语

本研究方法模拟的结果与文献[17]中的试验结果较为吻合，因此采用的本构模型与编制的分析程序是合理的。分析表明，圆钢管混凝土柱滞回曲线饱满，没有明显捏缩现象，具有良好的抗震性能。

含钢率对圆钢管混凝土柱抗震性能影响较大。随着含钢率的提高，柱的承载力、弹性阶段刚度会相应提高。

轴压比较小时，曲线几乎没有下降段，试件延性性能良好；当轴压比较大时，骨架曲线会有明显的下降段，极限位移、延性也会随着轴压比的增大而显著降低。故较大的轴压比对试件抗震性能不利。

随着钢材强度的提高，试件的承载力也会随之提高，但对柱弹性刚度几乎没有影响；对于非高强度混凝土，其强度对试件最大承载力、弹性阶段刚度影响效果不是很明显，故在一定强度范围内混凝土强度的提高对试件抗震性能的作用不大。

轴压比和含钢率对延性的影响较大，为了确保良好的抗震性能，设计时须对轴压比和含钢率进行相关限定。高层圆钢管混凝土结构轴压比较大，须采用较大的含钢率或较大的钢管壁厚。

[1] Susantha K A S，Hanbin Ge，Tsutomu Usami．Cyclic analysis and capacity prediction of concrete-filled steel box columns[J]．Earthquake Engineering and Structrual Dynamics，2002，31：195–216．

[2] 卢明奇．有限元法研究钢管混凝土框架的滞回性能[J]．武汉大学学报：工学版，2005，38(4)：59–62．

[3] 丁阳，许成祥，戴学新．钢管混凝土框架结构抗震性能的非线性有限元分析[J]．建筑结构，2004，34(1)：7–10．

[4] 孙修礼，梁书亭，段友利．钢管混凝土框架骨架曲线研究[J]．地震工程与工程振动，2007，27(1)：99–103．

[5] 张岚．基于OpenSees 的方钢管混凝土柱滞回性能数值模拟[J]．钢结构，2013，28(10)：6–11．

[6] Mari A，Scordelis A．Nonlineargeometric material and time dependent analysis of three dimensional reinforced and prestressed concrete frames[R]．Berkeley：SESM Report 82–12，Department of Civil Engineering，University of California，1984．

[7] Filippou F C，Issa A．Nonlinear analysis of reinforced concrete frames under cyclic load reversals[R]．Berkeley：EERC Report 88–12，Earthquake Engineering Research Center，1988．

[8] Mander J B，Priestley M J N，Park R．Theoretical stress-strain model for confined concrete [J]．Journal of Structural Engineering ， ASCE ， 1988 ， 114(8) ：1804–1825．

[9] 韩林海，钟善桐．利用内时理论描述钢管混凝土在复杂受力状态下核心混凝土的本构关系[J]．哈尔滨建筑工程学院学报，1993，26(2)：48–54．

[10] 藤智明，邹离湘．反复荷载下钢筋混凝土构件的非线性有限元分析[J]．土木工程学报，1996，29(2)：19–27．

[11] Karsan L D，Jirsa J O．Behavior of concrete under compressive loadings[J]．Journal of the Structural Divi- sion，ASCE，1969，95(ST12)：2543–2563．

[12] Susantha K，Hanbin Ge，Tsutomu Usami．Uniaxial stress-strain relationship of concrete confined by various shaped steel tubes [J]．Engineering Structures，2001，23：1331–1347．

[13] 蔡健，孙刚．方形钢管约束下核心混凝土的本构关系[J]．华南理工大学学报，2008，36(1)：105–109．

[14] Mohd Hisham Mohd Yassin．Nonlinear analysis of prestressed concrete structures under monotonic and cyclic loads[D]．San Fransico：University of California at Berekeley，1994．

[15] Yassin M H M．Nonlinear analysis of prestressed concrete structure under monotonic and cyclic loads[D]．Berkeley：University of California，1994．

[16] 何文辉．方钢管混凝土柱–钢梁组合框架抗震性能研究[D]．长沙：湖南大学土木工程学院，2009．

[17] Ahmed Elremaily，Atorod Azizinamini．Behavior and strength of circular concrete-filled tube columns [J]．Journal of Constructional Steel Research，2002，58：1567–1591．