新型电力线载波通信算法

陈晓娟，丛 鹏，程晓岩

(东北电力大学信息工程学院，吉林吉林132012)

0 引言

由于中国电力系统噪声污染严重，且非线性负荷的存在，电网载波信号传输过程中，会受到电网中噪声与谐波的干扰[1］。因此，检测出电网载波信号传输过程中的噪声信号与谐波信号，剔除噪声信号并针对谐波信号进行补偿有很重要的意义。比如傅里叶加窗插值法，由于其自身算法特点，通常可能导致检测出的谐波信号在准确性上大打折扣[2］。当前应用于谐波信号噪声消除方向的算法，通常采用的是小波变换，但将小波检测算法实际应用于国内电力系统时，分析检测出的谐波信号与噪声信号，观察到检测出的信号频带相互混叠，难以分析[3］。当传统谐波检测算法无法满足国内电力系统需求后，一些如信息融合、神经网络等新型谐波检测算法被提出，并应用于实际[4］。但提出的新算法，由于其自身算法复杂度较高，且需要在实际应用中进行训练构建网络以及大量先验知识，导致其在实际应用中冗余较大，且出现延时。

通过分析上述谐波检测方法存在的缺陷，本文提出了利用小波变换结合高阶累积量盲分离算法(WT-JADE算法)，首先降低电力线载波信号中存在的噪声，利用该算法检测谐波信号，检测出谐波信号后反向注入电网进行补偿。提出新算法克服了传统傅里叶变换方法频率分辨率低的缺点，较好地解决了单独使用小波检测谐波信号引起的频带混叠问题[3］，且与神经网络、支持向量机等方法相比，算法复杂度低，满足实时性要求。算法的实质是利用小波变换首先对载波信号进行降噪的预处理，保留源信号，之后将载波信号与噪声信号分离视为盲源分析，分离噪声信号，达到降噪目的。降噪后，将谐波信号与载波传输信号的分离视为盲源分析问题，检测出谐波信号并去除，从而有效达到了降噪和分离出谐波的效果。

1 WT-JADE算法检测原理

1.1 WT-JADE降噪原理

首先，对中国电力系统中的谐波信号进行分析，使用谐波检测装置得到谐波信号。通过对此信号进行分析，得到其是非平稳的信号特性，且其中含有较多噪声干扰。然后对算法进行选择，由于小波变换算法常应用于分析非平稳信号方面，其算法处理此类信号的结果对源信号信息损耗较小。与此同时，如果仅用小波变换算法处理谐波信号中的噪声信号，降噪的效果十分有限。因此，将谐波信号的降噪视为盲源分析问题，提出了小波变换与高阶累积量盲分离算法(JADE)对谐波信号进行降噪。JADE主要引入了多变量数据的四维累积量，对其做特征分解，降低了原小波变换算法的复杂度[5］。

一维含噪谐波信号模型:

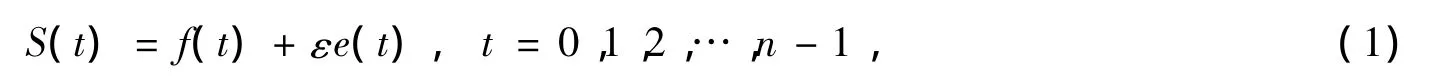
式中，S(t)为含噪谐波信号;f(t)为欲提取信号;e(t)为系统中存在的噪声信号;ε为噪声信号的比例系数。

其中，WT-JADE算法降噪步骤如下:

步骤1:首先运用小波对含噪的观测信号S(t)进行降噪预处理。

步骤2:对预降噪后的S(t)进行球化处理，得到球化矩阵W。

步骤3:联合对角化球化矩阵W的四阶累积量，得到酉矩阵U。

目前有很多学生对于语文的学习并没有很高的热情，这不利于提升语文教学的有效性。学生在整个学习过程中的全面发展与学习乐趣、积极性、教学质量等有着直接关联，鼓励性的评价体系可以让学生对语文学习充满更大的信心，让学生感受到学习的成就感，进而可以以更好的状态投入到学习中。教师在对学生进行评价时，一定要多使用鼓励性语言，对学生进行批评时也要委婉一些，以平和的、学生可以接受的方式进行，突出学生学习中的主体地位，让学生真正成为学习的主人，敢于探索未知的知识，体会到学习的快乐，慢慢树立起学习的自信心，提升学习的质量。

步骤5:对估计的源信号S'(t)进行盲源分离，得到二次降噪处理后的谐波信号X(t)。

该方法首先利用小波降噪方法进行降噪预处理，初步滤除谐波信号中含有的噪声，使得源信号较好保留。之后利用JADE算法对谐波信号和噪声信号进行有效的分离，达到二次降噪的目的，最大限度减少了小波消噪过程中谐波信号与噪声信号频带混叠的影响[3］。

1.2 WT-JADE联合检测谐波原理

当电力系统运行出现不稳定状况时，谐振干扰状况的发生使谐波信号具有突变性。小波变换理论由于其自身算法特点，当信号发生突变时，算法自身的局域化性质在检测谐波信号有其独特的优势[6］。但当谐波信号的多处奇异点相互重叠情况出现时，单独使用小波变换检测谐波的优势不明显。因此，提出WT-JADE联合检测谐波信号，首先利用小波进行分解重构预处理，之后JADE算法将谐波与基波视为盲源分离问题，WT-JADE检测算法对谐波基波以及谐波的各次谐波分量，便能准确测出[7］。

消噪后的谐波信号:

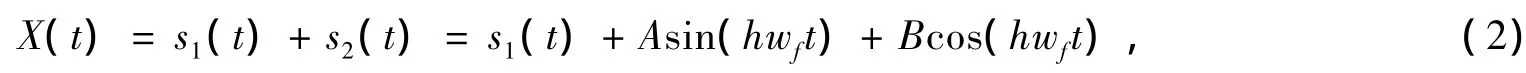
式中，X(t)为降噪后的谐波信号;s1(t)为分离出的基波信号;s2(t)为高次谐波信号;对谐波信号s2(t)的估计可以转化为对A和B的估计。

步骤1:选择最终观测信号Xi(t)的初值Xi(0)

2 仿真试验结果分析

对电网谐波信号进行模拟，创建载波信号:

其中，电力系统中主要存在奇数次的谐波信号，奇数次谐波信号以3次、5次、7次为主，故不含噪的谐波信号为:

混入SNR=30 dB的随机高斯白噪声信号:

其中，f为50 Hz的工频频率;S(t)为含噪的载波信号;t为时间。

加入噪声的电流谐波信号S(t)如图1所示。由图1可以发现:S(t)完全淹没在噪声中，不能直观地看出哪些是有用的信息。WT-JADE算法降噪后波形X(t)如图2所示。

通过图1和图2对比可看出:虽然混入噪声较大，单独使用小波降噪后波形效果不佳，故采用WTJADE算法进行降噪处理，图2中谐波信号WT-JADE降噪后波形明显，效果较好。

对X(t)谐波信号进行WT-JADE降噪处理后，分别利用单独使用小波变换方法和使用WT-JADE算法得到各层细节信号，如图3和图4所示。

通过图3和图4的对比可以看出:先利用小波变换提取谐波特征信号，之后采用WT-JADE算法对谐波信号进行盲源分离，与单独使用小波变换方法对小波分解系数进行处理相比，改进的WT-JADE算法能更好地保留细节信号。

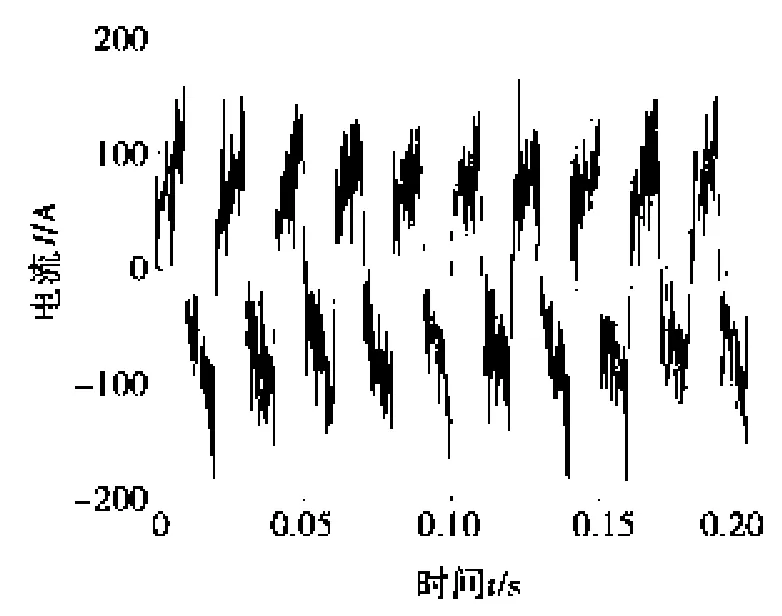
图1 含噪载波信号S(t)时域波形

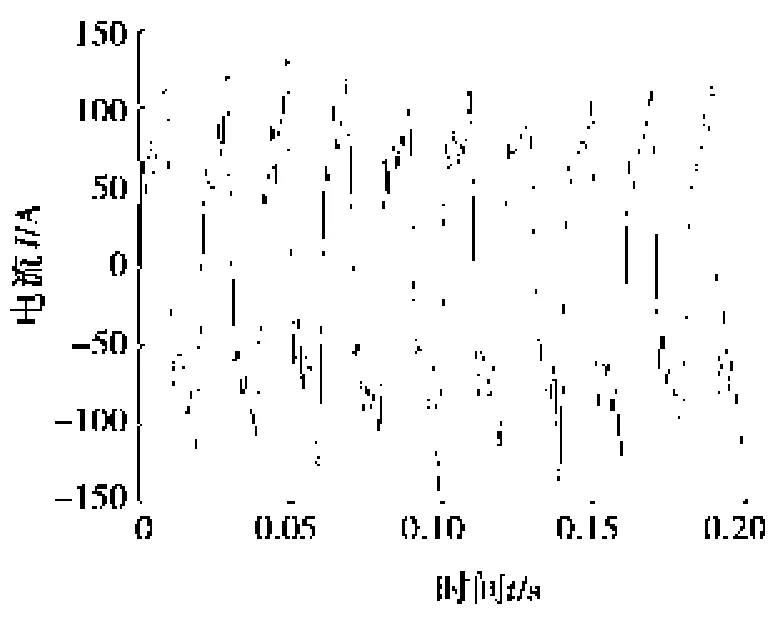
图2 WT-JADE联合降噪X(t)时域波形

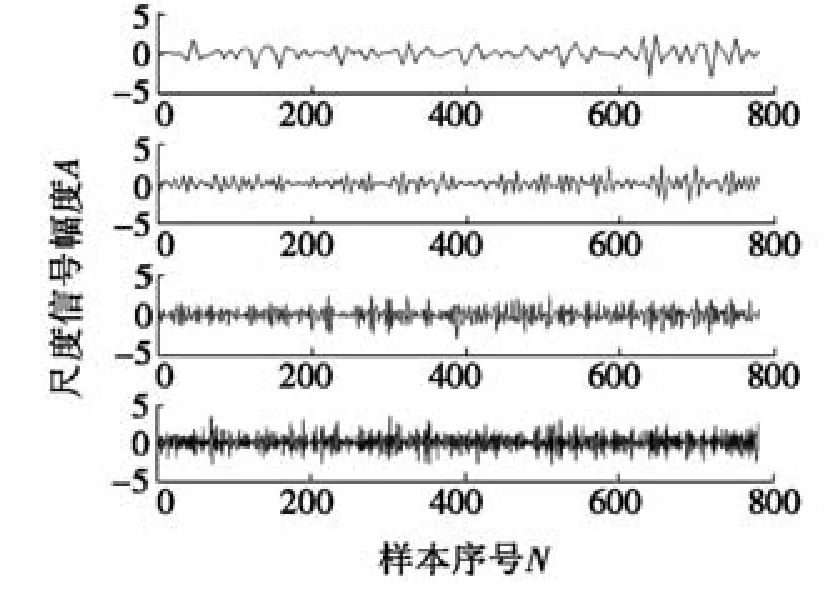
图3 小波变换分离各层细节信号

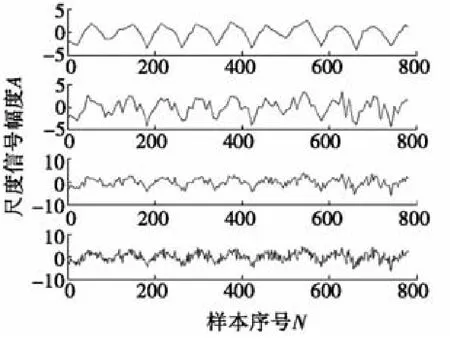
图4 WT-JADE分离各层细节信号

之后，将降噪后的谐波信号X(t)先进行小波分解重构的预处理，之后采用JADE算法进行盲源分离[8］，经过WT-JADE算法分离基波和谐波信号，处理后谐波信号如图5、图6所示。

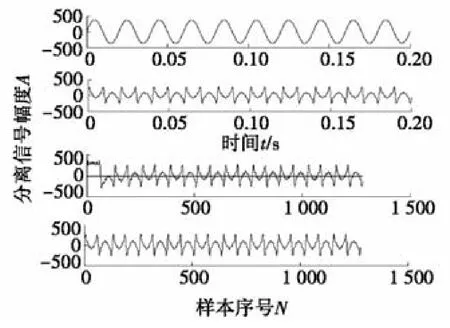
图5 分离出各层基波、谐波信号

图6 分离出高次谐波信号

由图5和图6可看出:图5中第1层分离出基波信号s1(t)，其他3层分别分离出3次、5次和7次谐波信号。图6中是3次、5次、7次混合的谐波信号s2(t)。该算法能较好分离出基波和谐波。

通过对分离出的谐波信号进行计算，通过有源滤波器，向电网中反向注入谐波信号进行补偿。补偿的信号如图7和图8所示。

图7 原始滤波器基波、谐波信号

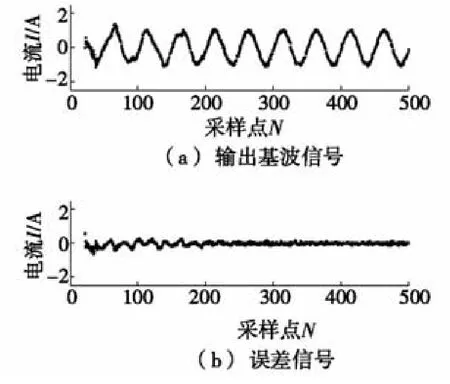
图8 滤波器补偿及误差信号

3 结论

由于中国电网中有较大的噪声污染，电网噪声和谐波的存在严重干扰电力线载波信号的传输。单独使用小波变换对载波信号进行降噪，降噪效果不理想，导致欲传输的信号部分失真[9］。WT-JADE算法与单独使用小波变换相比，更大限度降低了噪声的干扰。通过试验分析WT-JADE算法检测并分离谐波的效果表明:将谐波与载波信号的分离视为盲源分析问题，很好的保留了载波信号的重要信息，去除了谐波的干扰，失真程度很小，效果明显[10-11］。该方法对电网载波信号传输的研究有一定理论意义和实际参考价值。

[1]Angrisani L，D'Aponte P，D'Apuzzo M，et al.A Measurement Method Based on the Wavelet Transform for Power Quality Analysis[J］.IEEE Transactions on Power Delivery，1998，22(4):1112-1113.

[2]熊杰锋，王柏林，孙艳.奇异值与特征值分解在谐波源定阶中的等价性[J］.电测与仪表，2009，46(7):6-8.

[3]夏文静，傅行军.基于ICA在强背景噪声振动信号中的去噪研究[J］.汽轮机技术，2006，38(2):121-123.

[4]陈建华，周立鹏，李瑛.差分对非对称性对信号完整性及噪声的影响[J］.河南科技大学学报:自然科学版，2013，34(4):45-50.

[5]孙向文，孙立功.用于电力系统谐波频率高分辨估计的MUSIC算法[J］.电测与仪表，2008，45(10):19-21.

[6]赵佳，杨景曙，金家保.基于JADE算法的盲DOA估计[J］.通信学报，2010，31(8):91-97.

[7]王程刚.基于小波分析理论的电能质量扰动信号检测[J］.仪器仪表标准化与计量，2010(5):12-15.

[8]张贤达，保铮.盲信号分离[J］.电子学报，2001，29(12):1766-1771.

[9]文莉，刘正士，葛运建.小波去噪的几种方法[J］.合肥工业大学学报:自然科学版:2002，25(2):167-172.

[10]Paraschiv-Ionescu A，Jutten C，Aminian K.Wavelet Denoising for Highly Noisy Source Separation[C］//ISCAS.2002:201-214.

[11]张世平，赵永平，刘瑞叶.用基于全通滤波器的IIR陷波器抑制工频通信中的谐波干扰[J］.中国电机工程学报，2003，23(5):72-76.