高弹性锥体高速刀柄的性能研究*

张 淳 王 军 郭静涛 刘嘉兵 陈 冲

(燕山大学，河北 秦皇岛066004)

高速工具系统是实现高速加工的关键环节，其核心是刀柄，它是刀具与主轴的联接件，对定位精度和重复定位精度、刚度、动平衡及动态性能有较高要求。以往被广泛使用的7:24锥度BT刀柄由于采用单一锥面定位，高速离心膨胀使刀柄定位精度和联接刚度明显下降，无法满足高速加工要求［1-2］。

为了满足高速加工对刀柄的要求，各国研究者一直在探寻解决刀柄-主轴高速离心膨胀问题的方法，相继研发出新型高速刀柄，如德国的HSK、美国的KM、瑞典的CAPTO、日本的BIG-PLUS和NC5刀柄等。其中HSK是最具代表性的高速刀柄。它采取了锥面和端面双面定位、中空薄壁、1:10小锥度短锥结构，并利用中空柄部使用外涨式夹紧机构。该结构提高了锥柄的弹性变形能力，减小了主轴与刀柄的离心膨胀差，使双面定位易于实现，提高了刀柄定位精度、联接刚度，在一定程度上缓解了高速离心膨胀问题，但仍存在极限转速(通常指刀柄与主轴锥孔即将分离而不能保证径向定位时的转速)低、强度刚度低、锥柄易磨损、动态性能差、刀具悬伸量大等缺点［3］。国外学者对高速刀柄的性能也做了深入研究。加拿大M.Namazi等人采用有限元和试验方法揭示了不同刀柄拉紧力对主轴-刀柄系统动态性能的影响规律;美国J.S.Agaplou利用线弹性理论建立了主轴-刀柄联接的力学模型，计算了联接刚度随转速的变化规律;日本M.Tsutsumi试验研究了刀柄-主轴联接的接触压力分布规律和阻尼比变化规律，等等［4-6］。

国内对高速刀柄的研究主要集中在对国外以HSK为主的高速刀柄的性能分析和应用方面，尚未研制开发出实用的高速刀柄。如清华大学李光辉等人利用有限元方法研究了HSK-63A型刀柄预紧力、转速、过盈量等参数对刀柄-主轴连结性能的影响，并优化了其几何参数;山东大学艾兴等人运用弹塑性力学和非线性有限元技术分析了刀柄-主轴联接的受力变形和接触应力与转速和过盈量的关系，确定了最佳过盈量;江苏大学王贵成等人通过建立系统的动刚度模型，对HSK和KM刀柄与主轴的联接刚度、径向位移、接触压力进行了分析［7］。

现有高速刀柄存在的问题主要是极限转速、强度、刚度偏低。为改善其性能，设计了一种新型高弹性锥体高速刀柄。本文对其结构及性能进行介绍。

1 新型高速刀柄结构

新型高速刀柄的锥柄开有直槽和环槽(highspeed tool holder with straight and circular grooves，SCG)，结构如图1所示。刀柄采用双面定位、实心、1:10小锥度短锥结构。实心结构(指刀柄而非夹头部分)能够提高刀柄强度、刚度并减小刀具悬伸量。在锥体上开出直、环交错槽以提高锥柄的弹性，允许锥柄与主轴锥孔有较大的过盈量，又可增大锥体离心膨胀量，从而提高刀柄的极限转速。直槽沿周向均匀分布，环槽垂直于刀柄锥面，由多个凸起形成虚拟锥面。当刀柄与主轴联接时，凸起部分产生压缩与弯曲弹性变形，其中主要是压缩变形。选取标准拉钉LDA-45进行拉紧刀柄。为了与现有的高速刀柄兼容，SCG刀柄采用德国DIN69893标准HSK-E63刀柄(锥柄锥度为1:10)的外形尺寸。

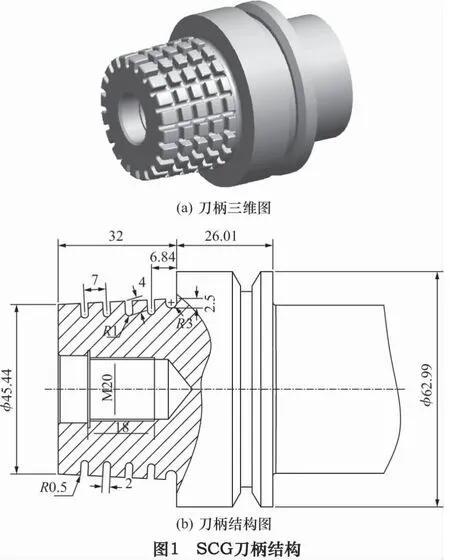
2 刀柄静态性能分析

刀柄采用锥面与端面双面定位夹紧，其接触压力包括锥面接触压力pc和端面接触压力pf，两者对刀柄性能的影响不同。锥面接触压力对刀柄的定位精度及极限转速起着决定作用，端面接触压力对刀柄的径向刚度和承载能力起主要作用［8］。为保证刀柄的综合性能，刀柄拉紧力(为实现双面接触定位拉紧机构施加于刀柄的轴向拉力)在锥面与端面的分配比例应保持在一定范围内，可类比HSK刀柄确定。锥面与端面的接触压力受刀柄锥体与主轴锥孔的过盈量以及刀柄与主轴的离心膨胀影响，而且两者相互制约。低转速时重点关注静态最大过盈量δmax下的端面接触压力pf，以确保刀柄-主轴联接具有足够的径向刚度;高速时需要关注最小过盈量δmin下的锥面接触压力pc，以保证锥面能够径向定位。

由于接触压力分布不均，分析时使用平均接触压力。而对于锥柄开槽的SCG刀柄，与HSK刀柄进行对比分析时采用等效接触压力，即折算为完整锥面上的压力，用pce表示。当进行单独分析时，仍采用平均接触压力pc。

建立刀柄与主轴的有限元模型，如图2所示。建模过程为:

(1)简化处理。因结构的对称性取1/4模型，不考虑刀柄的V型槽、刀具夹持部分及倒角、螺纹等细小结构。

(2)材料选择及参数设置。刀柄材料密度ρ=7 800 kg/m3，弹性模量E=196 GPa，泊松比v=0.25;主轴ρ=7 840 kg/m3，E=212 GPa，v=0.31。假定刀柄与主轴的材料均为理想弹塑性，摩擦系数μ=0.2。

(3)接触对及锥面配合过盈量的设置。设置端面与锥面两组接触对，接触类型为frictional。德国DIN69893标准推荐HSK-E63刀柄极限转速为34 000 r/min，过盈量为10.1～18μm;类比HSK根据有限元分析确定SCG刀柄的极限转速为42 500 r/min，过盈量为25μm～30μm。

(4)划分网格。在设置了接触后，Workbench自动进行网格划分，自动选取相应的单元设置。主轴结构较简单，采用扫略网格划分;刀柄结构较复杂，采用自由网格划分。

(5)施加约束及载荷。在主轴远离锥孔一侧的端面上施加全位移约束fixed support，刀柄与主轴的各自对称面上施加无摩擦约束frictionless support。类比HSK刀柄锥面与端面的刀柄拉紧力分配比例及压力大小，多次仿真计算确定SCG刀柄的拉紧力为25 kN。

HSK刀柄和SCG刀柄静态下的接触压力有限元结果如表1所示。由表可知，SCG刀柄在最小过盈量及最大过盈量下的锥面接触压力pce均比HSK刀柄大，而两者的端面接触压力也相差不大。由此可见，SCG刀柄的极限转速得到提高，且在静态及低转速下能够保证联接刚度和定位精度。

表1 静态时刀柄的平均接触压力

图3为刀柄在静态下、过盈量为30μm时刀柄锥面接触压力的分布情况。由图3可知，刀柄锥面两端接触压力较大，中间部分接触压力相对较小;锥面各凸起均处于接触状态，有利于保证定位精度和联接刚度;因应力集中导致凸起周边变形大于中间部位。刀柄最大接触压力为162.92 MPa，远小于刀柄材料的许用应力，故强度足够。

图4为静态时刀柄端面接触压力分布情况。由图可见，端面接触压力分布不均匀，从端面内径向外径边缘接触压力逐渐减小，此分布特点与HSK刀柄的端面接触压力分布相同。其原因为:静态时主轴的膨胀是由锥面的过盈配合导致的，在刀柄被拉紧过程中，主轴锥孔大径处即端部膨胀量相对较大，主轴端面会形成“凸”状，随后进入端面接触阶段，就出现了内径接触压力较大的现象。

3 刀柄高速性能分析

高转速时，刀柄和主轴因离心膨胀变形不同导致接触状况改变，影响联接性能，故需要分析刀柄与主轴在不同转速下的膨胀变形以及锥面和端面的接触压力状况。

3.1 刀柄锥面接触压力分析

对SCG刀柄在不同配合过盈量和转速下的锥面平均接触压力进行有限元分析，结果如图5所示。刀柄锥面平均接触压力随转速增加而减小，随过盈量的增大而增大。因为主轴的离心膨胀变形大于刀柄，随着转速的增加，这种差距越来越大;转速一定时，由离心力产生的锥面膨胀间隙也一定，故锥面接触压力由配合过盈量的大小决定。

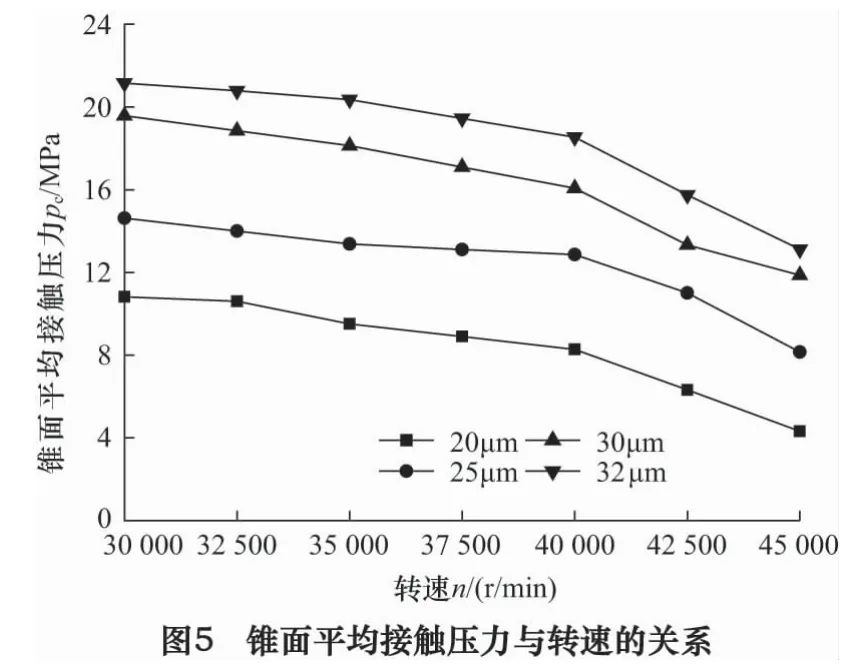
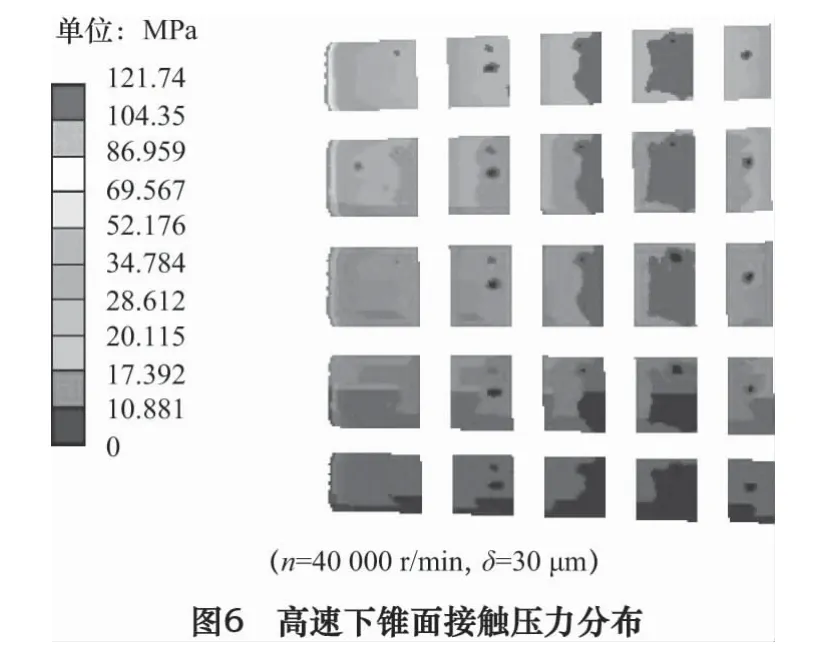
图6为转速40 000 r/min、过盈量30μm时刀柄锥面接触压力分布状况。就整个虚拟锥面而言，因高速离心膨胀使过盈量减小，平均接触压力比静态的小(图3所示);就局部而言，小端接触压力最大，从小端到大端逐渐减小，但大端边缘处小锥体接触压力值又略变大。这主要是因为越靠近刀柄大端处主轴锥孔越大、壁越薄，所以离心膨胀变形越大，与刀柄之间产生的间隙越大，进而锥面接触压力就小。而靠近大端处，主轴端面受到刀柄端面的摩擦阻碍作用，主轴锥孔的径向膨胀受到一定限制，加之刀柄本身大端边缘的应力集中，故大端的接触压力值稍大。

3.2 刀柄端面接触压力分析

对SCG刀柄端面平均接触压力进行有限元计算，端面接触压力随主轴转速和过盈量的变化情况如图7所示。端面接触压力随转速的提高而增大，随锥面过盈量的增大而减小。因为转速增加时锥面接触压力减小，刀柄拉紧力传递到端面的比例便增大;同理，过盈量越大锥面压力越大，因此端面压力相应有所减小。因端面接触面积较大，故转速和过盈量变化时，端面压力值变化范围并不大。

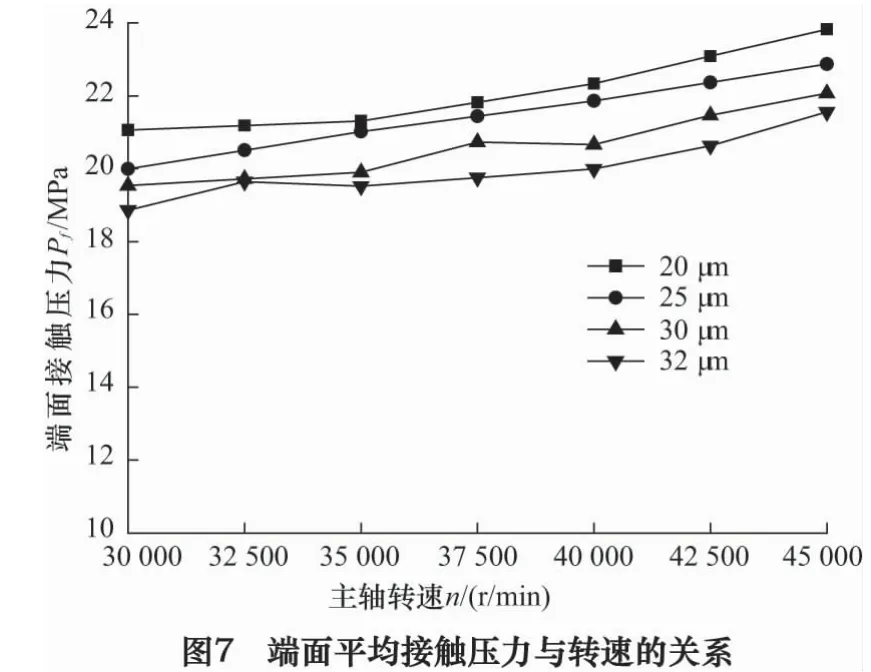
图8为转速40 000 r/min、过盈量30μm时刀柄端面接触压力分布状况。同图4对比可见，高速时端面的平均压力比静态时大;端面压力呈现由内径到外径逐渐增大的分布特点，这与刀柄-主轴静态联接时的端面压力分布相反。其原因是:随着转速的提高，主轴锥孔径向膨胀变形增大，传递到端面的夹紧力增大，使刀柄与主轴端面产生更大的摩擦力，阻止主轴膨胀变形，使主轴端面由静态接触时的“凸”状变成了“凹”状，因此使端面外缘接触压力变大。

3.3 主轴锥孔膨胀量分析

根据有限元分析结果得到主轴锥孔最大膨胀量与转速和过盈量的关系，如图9所示。主轴锥孔最大膨胀量为锥面接触压力、离心力和端面摩擦综合作用的结果。主轴锥孔膨胀量随转速的增加而迅速增加，这是因为由离心力产生的膨胀量与转速的平方成正比;过盈量增大，主轴锥孔膨胀量也增大，但影响较小。这与刀柄锥体具有较大的弹性有关，而且随着转速的提高，过盈量的影响越来越小，即在高速阶段离心力对主轴锥孔的膨胀变形起主要作用。由此可知，要想减小主轴锥孔膨胀量，应重点解决离心膨胀问题。

图10为转速40 000 r/min、过盈量30μm时主轴的径向膨胀变形图。由图可知，刀柄与主轴均发生径向变形。主轴锥孔前端膨胀量大，远离端部越来越小。

3.4 刀柄-主轴联接的径向刚度分析

刀柄-主轴联接刚度包括径向刚度、轴向刚度和扭转刚度。径向刚度值相比轴向刚度和扭转刚度较低，且对刀具寿命和加工质量影响较大，故需要分析刀柄-主轴联接的径向刚度。

为计量刀柄-主轴联接的径向刚度，而非刀柄与主轴系统的整体径向刚度，采用转角径向刚度计算方法。图11为刀柄-主轴联接的径向刚度计算示意图。点1、2取自距接触端面3 mm的刀柄断面上，点3、4取自主轴端面外径处。径向刚度及相关量的计算公式为式(1)～(5)。不在端面接触区域取点的目的是消除接触变形对转角的影响;也不在刀柄上距离接触端面较远处取点(例如图11的刀柄加载处)，因为受到刀柄悬伸部分的变形影响，将不能准确反映刀柄-主轴联接的径向刚度，而是刀柄的整体径向刚度。

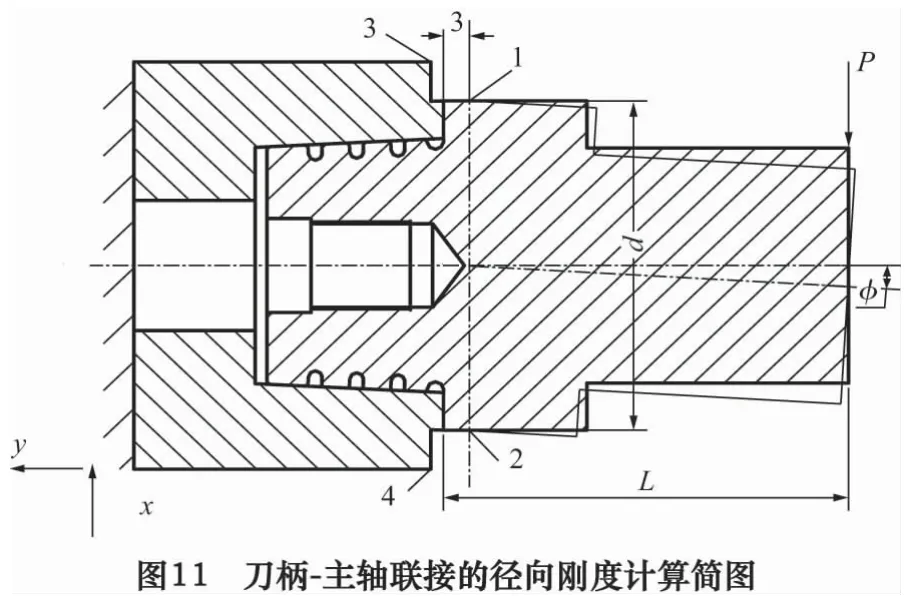
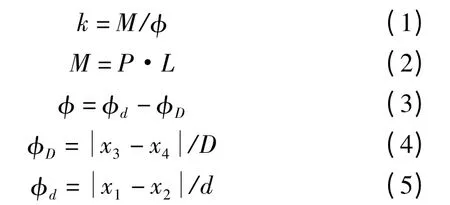
式中:k为刀柄-主轴联接的径向刚度;M为转矩;P为径向载荷，N;L为载荷作用点到刀柄端面距离，mm;D为主轴端面直径，mm;d为刀柄法兰直径，mm;φ为刀柄相对主轴端面的转角，mm/m;φD为主轴绝对转角，mm/m;φd为刀柄绝对转角，mm/m;x1、x2、x3、x4为点1～4x方向位移，mm。

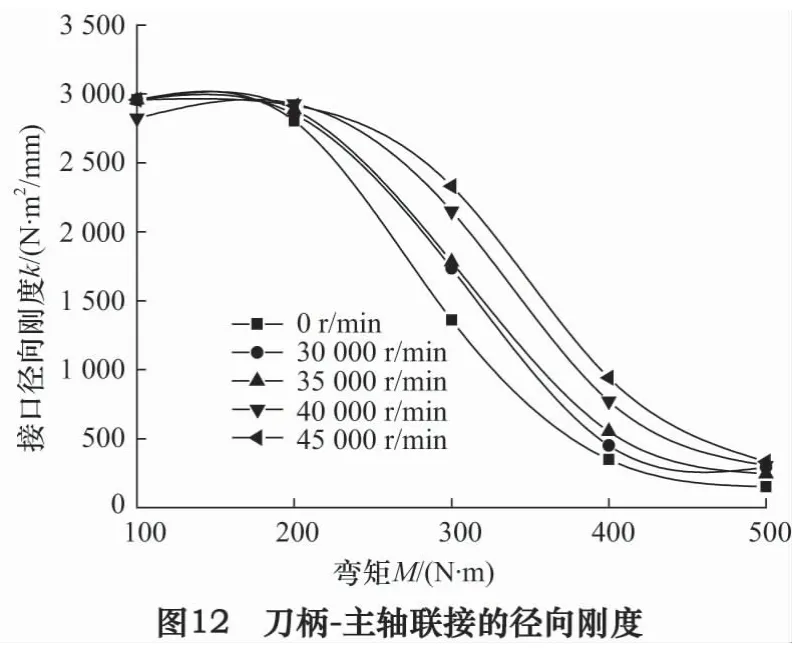
在有限元模型上需施加集中力P，L为100 mm。根据有限元结果计算转角值及径向刚度，绘制各转速下径向刚度随弯矩的变化曲线，如图12所示。

由图可知，弯矩(P与L乘积)较小时，径向刚度较大;随着弯矩的增加，径向刚度急剧下降。这是由端面接触状况决定的。弯矩较小时端面接触面积大，承受弯矩能力强;随着弯矩的逐渐增大，刀柄与主轴端面从一侧逐渐分离而失去支撑作用，故刚度迅速下降。当弯矩较小时，各转速下的径向刚度基本相同，此时端面接触良好;弯矩较大时，径向刚度随转速的提高而增大。其原因是高速时端面夹紧力变大，端面接触更加紧密，径向刚度得到提高。这一特性对提高刀柄-主轴联接的高速承载能力是有利的。

4 结语

通过对所设计新型高速刀柄的性能分析，得到如下结论:(1)该高速刀柄的锥体弹性增大，允许的配合过盈量大，刀柄的极限转速得到提高。(2)刀柄锥面两端接触压力较大，中间接触压力较小，锥面均处于接触状态，保证了定位精度和联接刚度。(3)端面接触压力呈不均匀分布。静态时端面压力从内径向外径接触压力逐渐减小，而高速时从内径向外径接触压力逐渐增大，此特性有利于提高高速时的径向刚度。(4)主轴锥孔膨胀量随转速和过盈量的增加而增加，高速时离心膨胀是关键因素，故预减小主轴锥孔膨胀量，应重点解决离心膨胀问题。(5)刀柄的径向刚度随载荷的增大而减小。载荷较小时，各转速下的径向刚度较高且基本相同;载荷较大时，刀柄径向刚度随转速的提高而增大，即高速承载能力增强。

［1］陈世平，李青锋.BT与HSK工具系统高速加工性能比较分析［J］.制造技术与机床，2012(4):157-159.

［2］曹宏瑞，李兵，陈雪峰.高速主轴离心膨胀及对轴承动态特性的影响［J］.机械工程学报，2012，48(19):59-64.

［3］张国军，臧运峰，吕枫.HSK刀柄和主轴的连接性能分析［J］.中国机械工程，2012，23(6):631-636.

［3］Gilovoi L Y，Molodtsov V V.Influence of centrifugal forces on the operation of HSK couplings［J］.Russian Engineering Research，2012，32(3):276-281.

［4］Agaplou J S.A methodology to measure joint stiffness parameters for toolholder-spindle interfaces［J］.Transactions of NAMRI/SME，2010(32):503-510.

［5］ULMER G.Doppelspindlig Schwerzerspanen in der HSK-A100-Klasse:Der dynamische Buffel［J］.Werkstatt+Betrieb:WB，2014，147(1/2):48-50.

［6］施东兴.高速加工中心主轴-工具系统联接特性研究［D］.镇江:江苏大学，2012.

［7］王军，曹景阳，吴凤和.新型大柔度锥面高速刀柄的设计［J］.制造技术与机床，2012(8):73-76.