龙门加工中心溜板动静态特性分析及优化*
2014-07-13张宝雷
陈 艳 张 松 陈 舟 张宝雷 满 佳
(①山东大学高效洁净机械制造教育部重点实验室,山东 济南250061;②山东永华机械有限公司,山东 兖州272100)
溜板是龙门加工中心的基础部件,起到承载、定位和连接的作用。其结构特征和性能对机床整机的加工精度,稳定性和抗振性具有重要影响,是机床优化设计的基础和关键。溜板通过螺钉固定在横梁导轨的滑块上,且承受滑枕及其附属部件的重力以及切削力,因此它必须具有足够的刚度来保证其加工精度。在材料确定的条件下,就要求其具有足够的强度来保证其刚度,这也就增加了溜板的质量。为了减轻溜板的质量而又满足强度、刚度和稳定性等要求,必须对结构进行优化设计[1]。
目前,国内对于机床机构一般采用经验设计,多数还停留在静态设计阶段,有关机床设计参数对其低阶固有频率影响的动态特性灵敏度分析却考虑不多[2]。对于机床结构的优化设计方法,主要采用尺寸优化与拓扑优化方法对结构进行轻量化设计与动静态特性的优化设计[3-4]。
本文建立了龙门加工中心溜板的有限元模型,以铣削加工时最大铣削力作为载荷边界条件,利用ANSYSWorkbench对其进行动静态特性分析。根据分析结果,采用整体尺寸优化与局部形状优化相结合的方法对其进行优化设计,达到其动静态性能改善,质量减轻的效果。
1 溜板的有限元模型
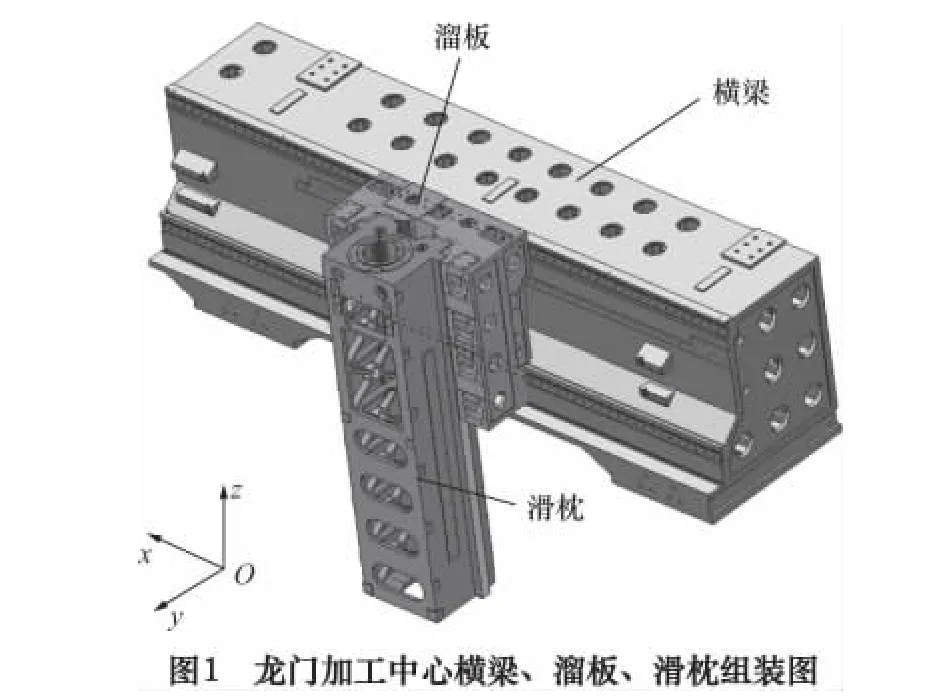
龙门加工中心主要由床身、立柱、横梁、溜板、滑枕等部件组成,图1为龙门加工中心横梁、溜板、滑枕的组装图。溜板通过螺钉与横梁导轨上的滑块相连接,滑枕及其附属部件通过丝杠支撑悬挂在溜板上完成Y方向的运动;且切削力通过滑枕及其他附属部件间接作用在溜板上,因此,溜板是龙门加工中心关键的承载和连接部件。
本文中采用三维建模软件SolidWorks对溜板进行三维实体建模,然后利用SolidWorks与有限元分析软件间优秀的双向传导功能,将其导入有限元软件中进行分析[5],如图2所示。为保证分析结果的准确性和提高分析效率,对溜板进行简化处理,去除对分析结果影响不大的倒角、圆角以及螺纹孔等。溜板的整体结构为铸造而成,材料为HT300,表1为材料参数。
2 溜板静态特性分析
溜板背面的5个面分别通过螺钉固定在横梁导轨的滑块上。因此,可在这5个面上施加固定约束作为约束边界条件,限制X、Y、Z方向上的移动(图3a)。


表1 HT300材料参数
铣削加工过程中,铣削力是不断变化的,本设计中只考虑铣削工况下溜板承受的
最大载荷。溜板所受的铣削力可通过施加远端力的方法施加在溜板上,力的初始位置设置在刀具位置处,则在力的作用面上将得到一个等效的力加上由于偏置的力所引起的力矩[6]。常规铣削工况下,溜板所受的最大铣削力分别为:进给力Fx=2 000 N,轴向力Fz=3 500 N,主切削力Fy=2 000 N(图3b)。
滑枕及其附属部件通过丝杠悬挂在支架上,由于龙门加工中心设有液压承载机构,因此溜板仅承受滑枕及其附属部件的一半重力,可通过施加远端力的方法施加在支架的上表面,力的作用点为滑枕及其附属部件组合的重心位置,大小为5 757.5 N。除此以外,溜板还要承受其自身的重力(图3b)。

溜板静态特性分析过程中,不考虑惯性和阻尼的影响,网格划分采用自动划分的方式。完成溜板的边界条件设置后,对其进行静力分析。HT300为脆性材料,根据第一强度理论,最大拉应力是引起材料脆断的主要因素,因此,在结果查看中设置显示溜板变形云图和第一主应力云图。
如图4所示,溜板最大变形位于其右侧导轨的下方位置处,最大变形量为0.002 94 mm。此处为溜板的薄弱环节,在后面的优化设计中可局部改善该处的结构以减小变形量。
如图5所示,溜板第一主应力最大位置在丝杠支架的前角位置处,最大第一主应力大小为σ1=1.990 5 MPa。主要是因为简化模型过程中将圆角和倒角等去除,从而造成该位置的应力集中,其余的应力主要在载荷承载部位,安全系数N=σb/σ1在20以上,其设计的安全系数较大[7],从应力分析的角度,材料抵抗破坏的能力还有很大的潜力,溜板还有很大的优化空间。


3 溜板动态特性分析
溜板的动态特性分析即溜板的模态分析,主要用于确定溜板的固有频率和振型,与其受载情况无关[8]。因此,在施加边界条件时,仅施加约束边界条件,不施加载荷边界条件。表2为溜板前4阶固有频率和各阶振型描述。图6为溜板前4阶振型云图。该型号龙门加工中心最大主轴转速为6 000 r/min,因此切削力引起的激振频率为100 Hz。溜板一阶固有频率为618.3 Hz,远远大于切削力引起的激振频率,溜板可完全避免共振,且一阶固有频率尚有可调节的空间。因此,本设计只选择一阶固有频率作为研究对象。

表2 约束状态下模态频率与振型

4 溜板优化设计
4.1 溜板尺寸优化设计
4.1.1 优化尺寸的选择
溜板整体采用长方体结构,内部为空腔结构,并设有筋板以增加其刚度,外壁与筋板上均设有减重孔,以减轻结构的质量。为了探索溜板的结构参数(外壁厚度、筋板厚度以及减重孔的尺寸等)对它的静态性能的影响,在不影响溜板的性能前提下确定优化尺寸的变化范围,并对它们进行灵敏度分析[9]。
针对溜板的结构特点,选取溜板的外壁厚度、筋板厚度以及减重孔的直径等13个尺寸作为预选的优化尺寸,如图7所示。各个尺寸的初始值和变化范围如表3所示。

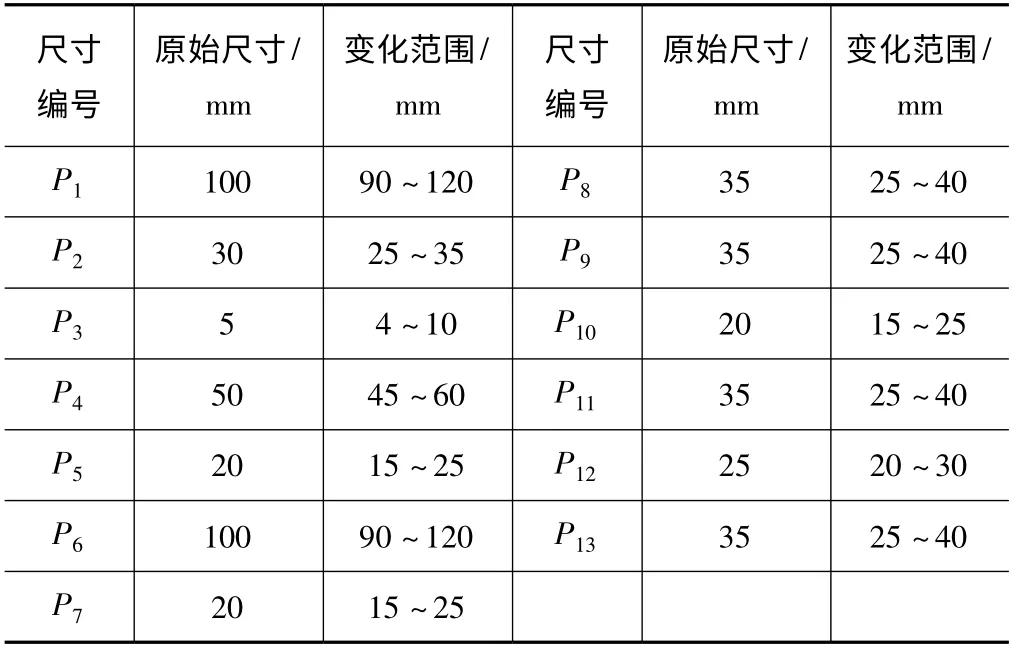
表3 各个尺寸的初始值和变化范围
4.1.2 优化尺寸的灵敏度分析
结构的灵敏度分析是分析结构性能参数Tj对结构设计参数xi变化的敏感性。即
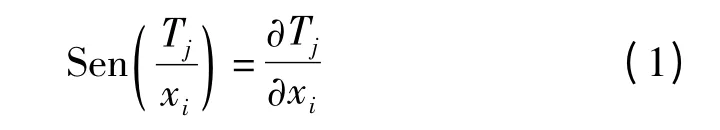
灵敏度的数值可以反映结构各设计变量对结构性能的影响[10]。灵敏度大表示尺寸的微小改变将导致结构该性能的极大变化,灵敏度小则表示尺寸即使有较大的改变对结构该性能也不会有较大的影响。

通过有限元计算,13个尺寸对溜板的质量、最大变形量、最大主应力以及一阶固有频率的灵敏度如图8所示。本文在尺寸优化阶段将减轻溜板的质量作为主要的优化目标,对于其他性能稍加改善。因此优化尺寸选择对质量灵敏度较高,对其他性能灵敏度较低的尺寸。通过对比,选出P3、P5、P7、P10、P11、P13等6个尺寸作为最终优化尺寸。
4.1.3 尺寸优化设计
在尺寸优化设计部分,设置质量最小化为目标函数,安全系数≥3,即最大第一主应力小于100 MPa,一阶固有频率大于等于618.3 Hz为约束条件。在后面的章节中将再次对尺寸优化后的溜板进行静态特性分析,根据分析结果,对溜板局部形状进行优化,因此该处暂不考虑溜板的最大变形量。优化后在满足约束条件的前提下,P3取最大值即P3=10 mm,其余尺寸取最小值,即P5=15 mm,P7=15 mm,P10=15 mm,P11=25 mm,P13=25 mm时溜板质量最小为763.84 kg,此时第一主应力最大值为1.990 4 MPa,一阶固有频率为
618.81 Hz。
4.2 溜板局部形状优化
对尺寸优化后的溜板模型再次进行静力分析,找出其变形量最大的位置,针对该位置进行局部形状优化,以达到减小其最大整体变形的目的。静力分析结果如图9、10所示。


通过静力分析可知,该工况下,溜板的最大整体变形出现在其箱体的右下侧位置,其变形量如表4所示。通过对比可知,溜板最大变形处Z方向的变形量远远大于其他方向的变形量,因此,为了减小结构的最大变形量,需要提高溜板在该位置处Z方向的刚性。本文针对溜板的结构特点以及其受力变形情况,提出以下3种局部加筋板优化方案(图11)。
方案一:“一”字型筋板,如图11b,筋板厚度为40 mm。
方案二:“十”字型筋板,如图11c,水平方向筋板厚度为40 mm,竖直方向筋板厚度为30 mm。
方案三:“X”型筋板,如图11d,筋板厚度为30 mm。
将3种方案分别进行有限元分析,结果如表5所示,可以看出:

表4 溜板最大变形处各方向的变形量


表5 3种方案结果对比
(1)3种方案的溜板的质量、第一主应力和一阶频率均相差不大。
(2)方案三的最大变形量明显大于方案一与方案二,方案一与方案二的最大变形量大小接近,主要是因为溜板的最大变形量出现在该侧壁左端的中间位置(图9),变形位移相对较大的节点呈水平方向分布,因此方案三与方案二中的竖直方向筋板对其影响不大,而方案一与方案二中的水平方向筋板对其影响较大。
(3)方案一比方案二加工方便。
因此,本设计采用方案一作为最终优化设计方案。
4.3 结果分析
优化设计前后的溜板结构动静态特性对比如表6。通过表6可以看出,优化后溜板质量减轻了50.65 kg,第一主应力与一阶固有频率均有所改善,最大总体变形量显著降低。因此,优化后溜板的动静态性能得到显著改善。

表6 优化前后有限元分析结果对比
5 结语
首先对龙门加工中心的溜板进行了静动态特性分析,得到了溜板的静态性能云图、前四阶固有频率与振型图。其次,对溜板结构的关键尺寸进行灵敏度分析,选出其中6个作为优化参数,以滑枕质量最小化为优化目标,以第一主应力与一阶固有频率为约束条件,对溜板进行整体尺寸优化设计。最后,以减小溜板的最大整体变形为目标对溜板进行局部形状优化设计,最终达到了溜板的动静态性能改善,质量减轻的目的。
[1]郑继红.复杂结构优化程序的研究与应用[D].重庆:重庆大学,1996.
[2]丛明,房波,周孜亮.车-车拉数控机床拖板有限元分析及优化设计[J].中国机械工程,2008,19(2):208-213.
[3]倪晓宁,易红,汤文成,等.机床床身结构的有限元分析与优化[J].制造技术与机床,2005(2):47-50.
[4]刘超峰,张淳,张功学,等.DVG850高速立式加工中心主轴箱拓扑优化设计[J].煤矿机械,2010,31(8):39-41.
[5]张伟.立式加工中心静动态特性分析及关键部件优化[D].大连:大连理工大学,2012.
[6]许京荆.ANSYS 13.0 Workbench数值模拟技术[M].北京:中国水利水电出版社,2012.
[7]陈庆堂.基于ANSYS的XK713数控铣床有限元分析及优化设计[D].南京:东南大学,2005.
[8]张力.模态分析与实验[M].北京:清华大学出版社,2011.
[9]周孜亮,王贵飞,丛明.基于ANSYSWorkbench的主轴箱有限元分析及优化设计[J].组合机床与自动化加工技术,2012(3):17-20.
[10]马迅,过学迅,赵幼平,等.基于有限元法的结构优化与灵敏度分析[J].机械科学与技术,2002,21(4):558-561.
