2n阶J-自伴算子的豫解算子及其谱分析

钱志祥

（肇庆科技职业技术学院基础教学部，广东肇庆526100）

2n阶J-自伴算子的豫解算子及其谱分析

钱志祥

（肇庆科技职业技术学院基础教学部，广东肇庆526100）

基于具有可积复系数函数的2n阶线性微分方程解的渐近式，讨论了复系数2n阶微分方程平方可积解的个数与其最小算子的亏指数，再利用2n阶J-自伴算子的豫解算子的性质，研究2n阶J-自伴算子的谱，得出了一个与实系数情形类似的重要结论。

微分算子；J_自共轭算子；豫解算子；谱分析

引言

J-自共轭微分算子谱理论的研究，始于对耗散算子和具有复势能薛定谔算子的研究，复势能算子在量子力学中具有重要的应用，因此，复系数算子的谱理论近些年来备受人们的关注。因为J-自共轭微分算子是非自伴的，所以其谱理论的研究有一定的难度，目前，对J-自共轭算子的谱理论的研究所采用的方法也十分有限，尽管许多数学家在这方面已经做了大量的工作，取得了丰富的成果，但是其谱理论还很不完善。本文通过讨论具有可积复系数的2n阶微分方程平方可积解的个数与其最小算子的亏指数，再利用2n阶J-自共轭微分算子的豫解算子的性质，研究了2n阶J-自共轭算子的谱，得到了这一类算子谱的分布。

考虑阶J-对称微分表达式：

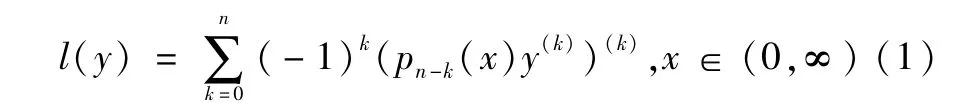
其系数满足下列条件：是定义在（0，∞）上的复值函数，而且pk，1（x），pk，2（x）∈L2（0，∞）k=1，2，…，n。

定义1［1］定义算子TM：TMy=l（y），D（TM）=｛y∈L2（a，b），y（k）在（a，b）上绝对连续，0≤k≤n-1，l（y）∈L2（a，b）｝称TM为由微分算式l（y）生成的最大算子。定义算子T′0：T′0y=l（y），D（T′0）=｛y∈D（TM），y在（a，b）内具有紧支柱｝，T′0的闭包记为T0，称算子T0为由微分算式l（y）生成的最小算子。

引理1［2］设函数在区间［0，∞）上可积，且则方程

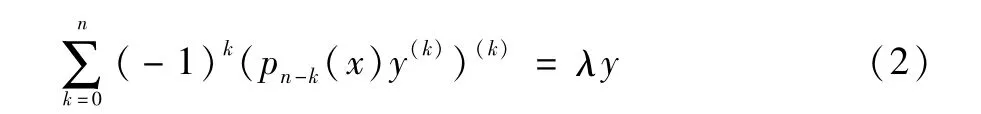
有2n个线性无关的解，yk（k=1，2，3……，2n）当x→∞时，它们的渐近性为：

yk=eμkξ［1+o（1）］k=1，2，……，2n

其中，μk为（-1）nλ的所有不同的2n次方根，其实部各不相同，而t；而且由（2）式生成的最小算子T0是J-对称算子，其亏指数等于n。

引理2［3_5］设算子T的亏指数为d（T）=m＜∞，D（T）⊂D⊂D（JT*J），D是T的某个J自伴延拓的定义域的充要条件是：存在｛x123m使得：

（1）｛x1，x2，x3…，xm｝模D（T）线性无关；

（2）［xj，xk］=0，j，k=1，2，3，…，m；

定义2［6］用σ（T），ρ（T）分别表示算子T的谱集和正则集，则集合Cσ（T）=ρ（T），其中C表示复平面，X表示全空间。σ（T）可以分解成互不相交的集合σp（T），σc（T）和σr（T）的并集，其定义如下：

它们分别称为算子T的点谱、连续谱和剩余谱。

引理3［7］若算子T是一个J-自伴微分算子，则算子T的剩余谱是空集σr（T）=φ，此时算子T的谱可分为离散谱和本质谱σ（T）=σd（T）∪σe（T）。

1 主要结论

引理4若（1）式的系数满足（Ⅰ）（Ⅱ），则由

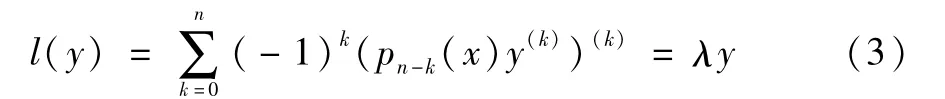
在其J-自伴定义域D内生成的算子T是一个J-自共轭算子。当λ∈［0，∞）时，方程（3）在L2［0，∞）中的线性无关解的个数为n-1小于其最小算子T0的亏指数n。当λ∈C-［0，∞）时，方程（3）在L2［0，∞）中的线性无关的解的个数为n恰好等于其最小算子T0的亏指数n。

证明根据引理1知，由（3）式生成的最小算子T0是J-对称算子，其亏指数等于n，且对∀λ∈C，方程有2n个线性无关的解yk（k=1，2，3……，2n）；当x→∞时，它们的渐近性如下：yk=eμkξ［1+o（1）］k=1，2，……，2n其中μk为（-1）nλ的所有不同的2n次方根，其实部各不相同，而ξ=t，根据引理2知由（1）式在定义域D（T）中生成的算子是J-自共轭算子T，令则μk=，从而当x→∞时，yk=esξωk

［1+o（1）］k=1，2，……，2n。

（1）当λ∈［0，∞）时

当Reλ＞0，而argλ=0时，μk=seiθk（k=0，…，2n，因为argλ= 0，所以，当n为奇数时，

当n为偶数时，

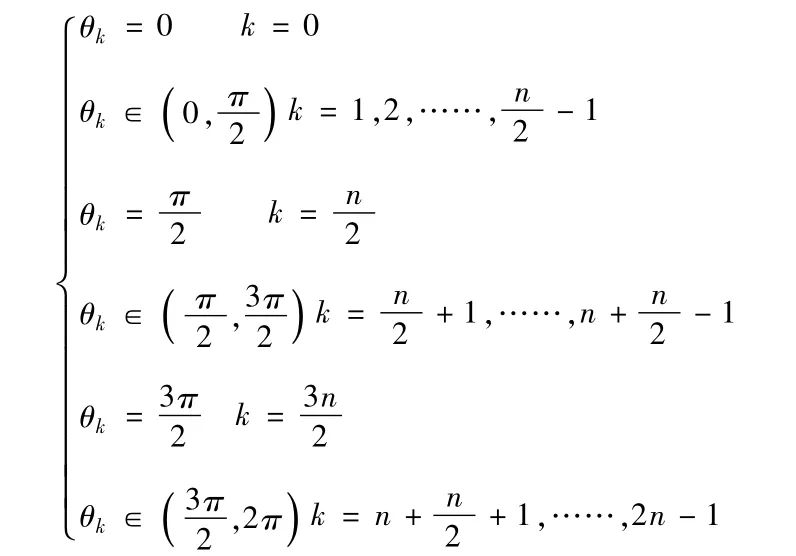
根据这2n个角θk（k=0，1，……，2n-1）在平面直角坐标系中的分布，按μk的实部进行排序，

设ρi=Reμi，当1≤i≤n-1时，ρi=Reμi＜0，yi= eμiξ［1+o（1）］∈L2［0，∞），当n≤i≤2n时，ρi=Reμi≥0，yi=eμiξ［1+o（1）］∉L2［0，∞），故此情形下方程（3）在L2［0，∞）中的线性无关解的个数为n-1小于算子T0的亏指数n

（2）当λ∈C-［0，∞）时

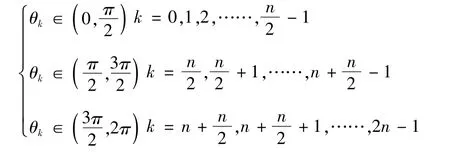
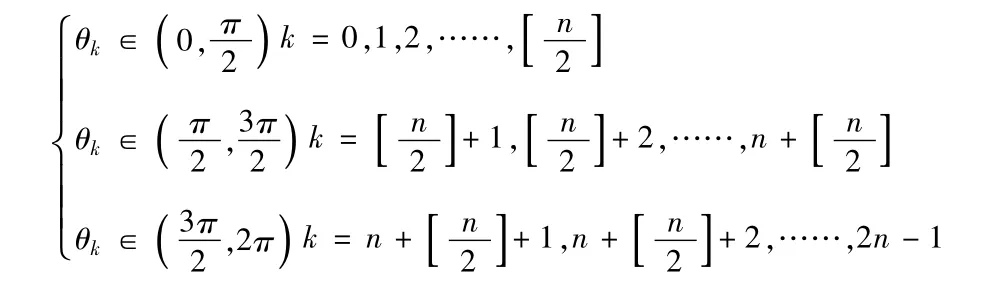
当n为奇数时，根据这2n个角θk在平面直角坐标系中的分布，按μk的实部进行排序，

Reμ1≤……≤Reμn＜0≤Reμn+1≤……，≤Reμ2n设ρi=Reμi，当1≤i≤n时，ρi=Reμi＜0，yi=eμiξ［1+o（1）］∈L2［0，∞），当n+1≤i≤2n时，ρi= Reμi＞0，yi=eμiξ［1+o（1）］∉L2［0，∞），故此情形下方程（3）在L2［0，∞）中的线性无关解的个数恰好等于算子T0的亏指数n。

当n为奇数时

根据这2n个角θk（k=0，1，……，2n-1）在平面直角坐标系中的分布，对μk的实部进行排序，

Reμ1≤……≤Reμn＜0≤Reμn+1≤……≤Reμ2n设ρi=Reμi，当1≤i≤n时，ρi=Reμi＜0，yi=eμiξ［1+o（1）］∈L2［0，∞），当n+1≤i≤2n时，ρi= Reμi＞0，yi=eμiξ［1+o（1）］∉L2［0，∞），故此情形下方程（3）在L2［0，∞）中的线性无关解的个数恰好等于算子T0的亏指数n。

Reμ1≤……≤Reμn＜0≤Reμn+1≤……≤Reμ2n设ρi=Reμi，当1≤i≤n时，ρi=Reμi＜0，yi=eμiξ［1+o（1）］∈L2［0，∞），当n+1≤i≤2n时，ρi= Reμi＞0，yi=eμiξ［1+o（1）］∉L2［0，∞），故此情形下方程（3）在L［0，∞）中的线性无关解的个数恰好等于算子T0的亏指数n。

④当Reλ＜0，而argλ=π时，μk=seiθk，其中θk=，经过简单分析知这2n个角θk（k=0，1，……，2n-1）在平面直角坐标系中的分布，对μk的实部进行排序，

Reμ1≤……≤Reμn＜0≤Reμn+1≤……≤Reμ2n设ρi=Reμi，当1≤i≤n时，ρi=Reμi＜0，yi=eμiξ［1+o（1）］∈L2［0，∞），当n+1≤i≤2n时，ρi= Reμi＞0，yi=eμiξ［1+o（1）］∉L2［0，∞），故此情形下方程（3）在L2［0，∞）中的线性无关解的个数恰好等于算子T0的亏指数n。

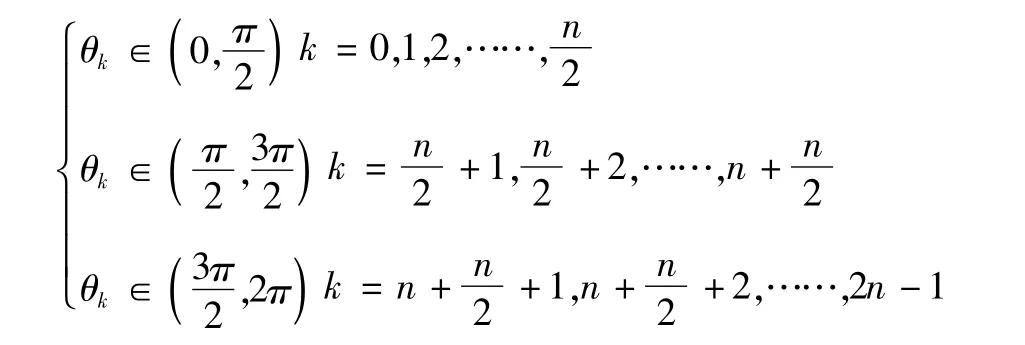
当n为奇数时，

根据这2n个角θk（k=0，1，……，2n-1）在平面直角坐标系中的分布，对μk的实部进行排序，

Reμ1≤……≤Reμn＜0≤Reμn+1≤……≤Reμ2n设ρi=Reμi，当1≤i≤n时，ρi=Reμi＜0，yi=eμiξ［1+o（1）］∈L2［0，∞），当n+1≤i≤2n时，ρi= Reμi＞0，yi=eμiξ［1+o（1）］∉L2［0，∞），故此情形下方程（3）在L2［0，∞）中的线性无关解的个数恰好等于算子T0的亏指数n。

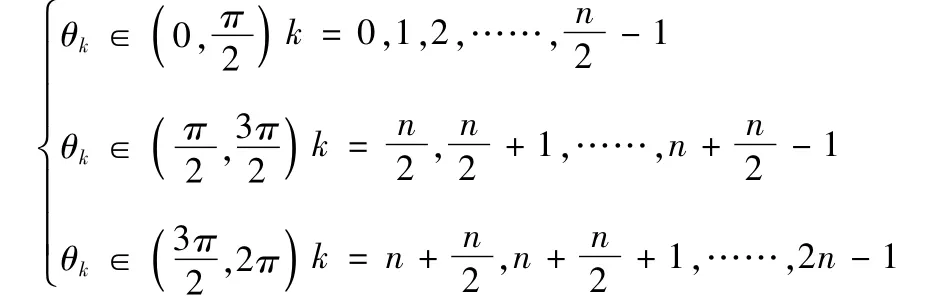
当n为奇数时，

根据这2n个角θk（k=0，1，……，2n-1）在平面直角坐标系中的分布，对μk的实部进行排序，

Reμ1≤……≤Reμn＜0≤Reμn+1≤……≤Reμ2n设ρi=Reμi，当1≤i≤n时，ρi=Reμi＜0，yi=eμiξ｝∈L2［0，∞），当n+1≤i≤2n时，ρi=Reμi＞0，yi= eμiξ［1+o（1）］∉L2［0，∞），故此情形下方程（3）在L2［0，∞）中的线性无关解的个数恰好等于算子T0的亏指数n。

根据①～⑥的讨论可知：当λ∈C-［0，∞）时，方程（3）在L2［0，∞）中恰有n个线性独立的解。

综合（1）、（2），于是引理4得证。

引理5［S］设y1（x），y2（x），y3（x）…y2n（x）是齐次方程（l-λI）y=0的基本解系，f（x）可测且在［0，∞）上局部可积，那么非齐次方程（l-λI）y=f的通解形式为：

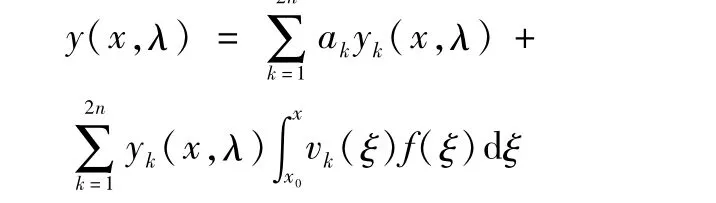
其中，a1，a2，a3…，a2n是任意常数，而函数

其中，W（y1，y2，…，y2n）表示函数y1（x），y2（x），y3（x），…，y2n（x）的朗基行列式。

证明过程见文献［S］中引理4。

定理1［S_9］2n阶J-自伴微分算子T在一端奇异情况下的豫解算子（T-λI）-1是一个积分算子。其形式为：

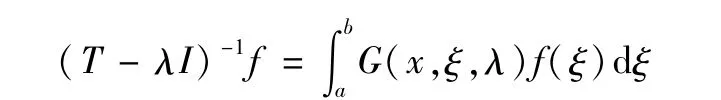
其中

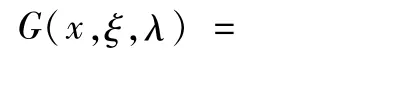
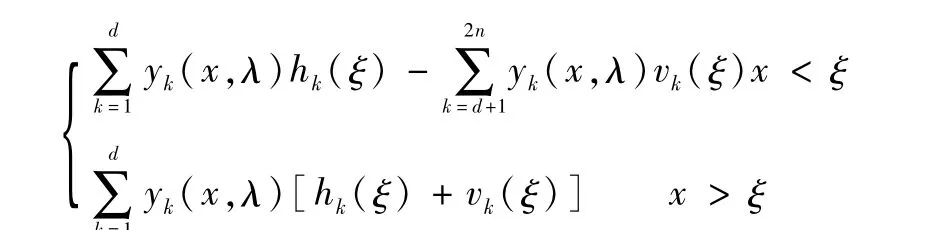
d为最小算子T0的亏指数。

证明过程见文献［S］定理2。

定理2若（1）式的系数满足（Ⅰ）（Ⅱ），定义域满足引理2，则由

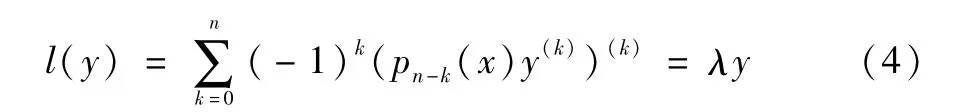
J-自共轭扩张所生成的算子T是一个J-自共轭算子。如果对于复数λ，方程（4）在L2［0，∞）中的线性无关解的个数小于其最小算子T0的亏指数，则这个值λ属于算了T0的连续谱；如果对于复数λ，方程（4）在L2［0，∞）中的线性无关解的个数等于算子T0的亏指数，则这个值λ属于算了T0的离散谱。

证明由引理1和引理2知算子T是一个J-自共轭算子，且其最小算子T0亏指数为n。由定理1知（4）式的豫解算子为，其中，

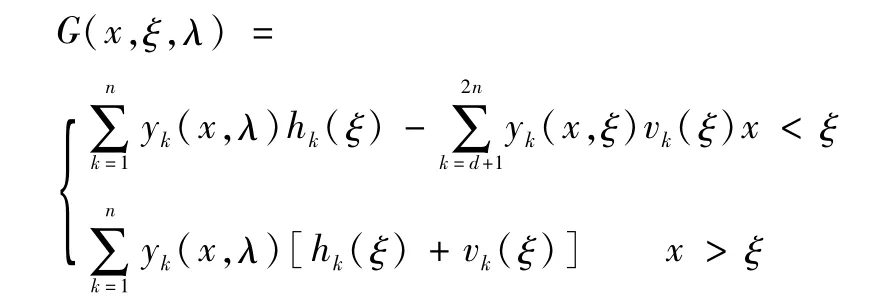
n为最小算子T0的亏指数，它是以G（x，ξ，λ）为核的积分算子，对区间［0，∞）中的一切x，任意固定的ξ，当x＞ξ时，核G（x，ξ，λ）为L2［0，∞）中的y1（x），y2（x），y3（x），…，yn（x）的线性组合，即λ）［hk（ξ）+k（ξ）］，由引理4知当λ∈［0，∞）时，方程（4）在L2［0，∞）中的线性无关解的个数只为n-1，小于算子T0的亏指数n，所以y1（x），y2（x），y3（x），…，yn（x）中只有n-1个属于L2［0，∞），有yk（x）∉=∞，所以在这种情况下，其豫解算子是无界的，由定义2知这时λ的值属于算了T0的连续谱。当λ∈C-［0，∞）时，方程（4）在L2［0，∞）中的线性无关的解的个数为n，等于算子T0的亏指数n，这时y1（x），y2（x），…，yn（x）∈L2［0，∞），故

所以在这种情况下，其豫解算子是有界的，结合引理3这时λ的值应属于算了T0的离散谱。

推论1［10］若（1）式的系数是区间（a，b）上可测的实函数，且在它的每一个有限闭子区间［α，β］中可积的，对于复数λ，方程l（y）=λy在L2（a，b）中的线性无关解的个数小于算子L0的亏指数，则这个值λ属于算子L0的谱的核，因此，如果这个值λ不是算子L0的特征值，则它属于L0的所有自共轭扩张谱的连续部分。如果端点a或端点b中之一是正则的，那么，后者总是成立的。

［1]Glazman IM.DirectMethods of Qualitative Spectral A_ nalysis of Singular Differential operators［M].Jerusalem: Israel Program for Scientific Translations，1965.

［2]王忠，付守忠.线性算子谱理论及其应用［M].北京:科学出版社，2013.

［3]刘景麟.关于J对称算子的J自伴延拓［J].内蒙古大学学报:自然科学版，1992，23(3):312_316.

［4]姜凤利，赵晓颖.J_对称微分算子自共域的辛风何刻画（I）［J].辽宁石油化工大学学报，2011，31(1):72_ 75.

［5]王忠，杨瑞芳.高阶J-自伴微分算子的豫解算子［J].内蒙古大学学报:自然科学版，1997，28(3):330_334.

［6]孙炯，王忠.线性算子的谱分析［M].北京:科学出版社，2005.

［7]Muller P E.Spectral theory of ordinary differential oper_ ators［M].Chichester:Ellis Hopwood Limited，1981.

［8]刘肖云，王忠.奇异2n阶J_自伴向量微分算子的预解算子［J].内蒙古大学学报:自然科学版，2007，38(1): 7_12.

［9]刘肖云，王宜静.有限区间上两项二阶向量微分算子的特征函数［J].安阳工学院学报，2013，12(2):91_ 94.

［10]Naimark M A.线性微分算子［M].北京:科学出版社，1964.

Resolvent Operator and Spectrum Analysis of the 2n_order J_self_adjoint Operator

QIAN Zhixiang
（DePartment of Basic Education，Zhaoqing Science and Technology Polytechnic，Zhaoqing 526100，China）

Based on the asymPtotic exPression of the solution of 2n order linear differential equation who has integrable Plural coefficients functions，the number of square integrable solutions and the deficiency index of theminimum oPerator of2n order differential equation with comPlex coefficients are discussed.Then，the ProPerties of the resolvent oPerators are used to study the sPectrum of the 2n_order J-self_adjoint differential oPerator.An imPortant conclusion that the ProPerty is similar to that of the real coefficients J-symmetric differential oPerator is obtained.

differential oPerator；J-self_adjoint differential oPerator；resolvent oPerator；sPectrum analysis

O175.3

A

1673_1549(2014)02_0091_05

10.11863/j.suse.2014.02.20

2013_11_29

广东省高层次人才培养项目（9251064101000015）

钱志祥（1974_），男，安徽巢湖人，讲师，硕士，主要从事没微分算子理论方面的研究，（E_mail）qzx20062006@126.com