一元连续变限函数的求导
2014-07-12熊良鹏
熊良鹏
(成都理工大学 工程技术学院,四川 乐山 614007)
一元连续变限函数的求导
熊良鹏
(成都理工大学 工程技术学院,四川 乐山 614007)
探讨了一元连续变限函数中关于单一变限、上下复合变限及混合变元4类不同情况下的求导方法与技巧,给出了各类变限函数的一般求导公式,并通过实例表明了这些方法的重要性.
连续函数;变限函数;定积分
牛顿-莱布尼兹公式是高等数学中定积分计算的主要理论基础,该公式的推导以连续变限函数的性质为前提,但变限函数的导数具有特殊性和灵活性,而教材对变限函数的介绍又比较简单,无法满足实际处理相关深层次问题的需要. 事实上,如果函数f(x)在闭区间[a,b]上连续,则f(x)在[a,b]上一定可积,为此任取x∈[a,b],显然函数在[a,x]⊂[a,b]上连续且可积,即定积分存在,需要注意的是,这里的上限x与积分变量x含义不同,形式上可以等价地记此定积分为,这是一个关于变量x的函数:

这里称Φ(x)为变上限函数,类似可以定义变下限函数,二者统称为变限函数.
文献[1-2]给出了一个关于Φ(x)的重要性质:如果函数f(x)在闭区间[a,b]上连续,则一定在[a,b]上可导,且Φ′(x)=f(x),a≤x≤b. 文献[3-5]也从不同的角度研究了变限函数的各种性质. 本文在前期文献研究的基础上,主要针对变限求导的各类形式作了逐步深入的探讨和总结,并通过具体的例子巩固了处理相关问题的方法和技巧.
1 主要结果
证明 这个函数的特点是下限在发生变化,但根据定积分的性质可以转化成前述简单形式,即
如果将定理1中的单一变量x推广到关于x的复合可导函数φ(x),此时函数最终变量依然是x,因此在处理求导问题时必须对复合函数进行相应的求导.
定理2 设函数f(x)在[a,b]内连续且u(x),v(x)均为可导函数,若复合变限积分函数Φ1(x)=都存在,则一定有:Φ1′(x)=u′(x)f[u(x )],Φ2′(x)=-v′(x)f[v(x)].
证明 定理1的证明过程暗示这里只需要对Φ1(x)的导数公式给予证明即可. 因为Φ1(x)=

因为f(t)在以u(x)和u(x+Δx)为端点的区间内连续,由积分中值定理,则至少存在一点ζ介于u(x)与u(x+Δx)间,且使得ΔΦ1=f(ζ)[u(x+Δx)-u(x)],于是
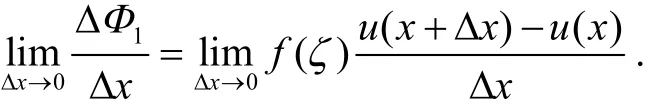
事实上,当Δx→0同时有ζ→u(x), 且f(x)连续、u(x)可导,因此

定理1和定理2为常见的变限求导形式,复合变限的求导公式可推广到如下更一般的形式.
推论1 设函数f(x)在[a,b]内连续且u(x),v(x)均为可导函数,若上下复合变限积分函数Φ(x)=存在,则Φ′(x)=u′(x)f[u(x)]-v′(x)f[v(x)].
证明 任取一数c,由定积分的分段可加性有:

如果将推论1中的被积函数f(t)用变限函数的形式替换,直接可以得到推论2.
推论2 设φ1(x),φ2(x)为可导函数,且定义
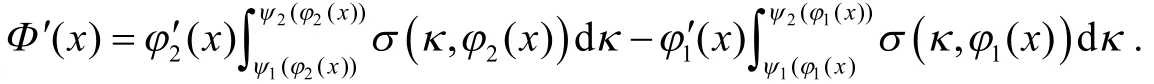
上面讨论了单一变量或复合变量作为被积函数时导数的求取,但有时我们会面临混合变量的情况,这时需要通过变量分离或者变量替换等方法将其转化为熟悉的形式.
定理3 设函数f(x)连续且u(x),v(x)均为可导函数,m,n为实数,若混合变元积分Φ(x)=
证明 定理中函数Φ(x)的上下限都是复合变限,并且被积函数是变量x与t的混合形式. 通过变量分离(注意这里真正的积分变量为t)有:

所以

证明完成.
定理3中被积函数容易变量分离,处理起来比较方便,如果无法分离,那就只有通过变量替换实现变量归一.

证明 这里函数Φ(x)中被积函数f(mx-nt)无法变量分离,为了实现变量归一,设ρ=mx-nt,于是t:v(x)→u(x),对应新变量ρ的范围ρ:mx-nv(x)→mx-nu(x),因此
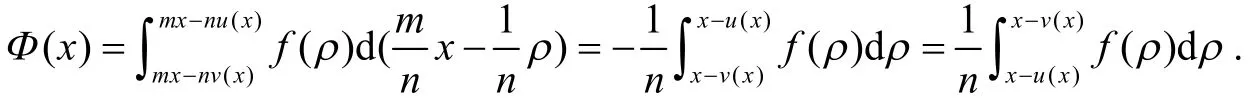
证明完成.
2 应用
变限函数的求导是微积分中非常重要的知识点,形式上灵活多变,下面列举几例对前面的讨论进行分析和应用.

上面的步骤连用了两次罗必塔法则,并且最后一步用到等价量tanx~x(x→0).
分析:本例是一个被积函数为混合变元的变限函数,属于定理3可以变量分离的情况.
解 函数f(x)的定义域为(-∞,+∞),先讨论函数所有可能的单调区间临界点. 首先对函数变元分离,即于是由定理3,
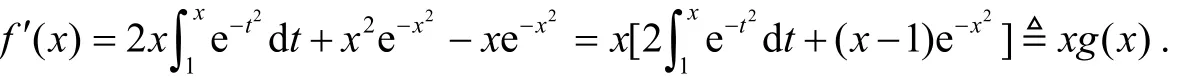
容易看出f′(1)=0,f ′(0)=0. 而且易见:
因此,在(-∞,0)上,f′(x)>0,f(x)单调递增;在(0,1)上,f′(x)<0,f(x)单调递减;在(1,+∞)上,f′(x)>0,f(x)单调递增.
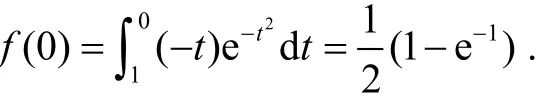
分析:这个复合变限函数的被积函数是不可分离的混合变元,可以直接用定理4的公式进行处理.
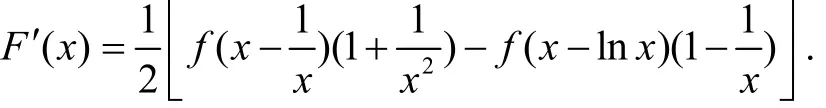
3 总结
对被积函数为单变元且积分变限单一(包括复合)的情形求导,一定要遵循先代后导的原则,且要注意符号;如果积分为变限且被积函数有混合变元时,必须清楚积分变量和最终函数变量是不同的. 值得注意的是关于变限函数的求导还会碰到一些复杂的情况,但基本能够通过等价变形或者变量替换等方式转化为定理1~4的情形来解决.
[1] 同济大学数学系. 高等数学:上册[M]. 6版. 北京:高等教育出版社,2008: 237-238.
[2] 李正元,李永乐. 数学复习全书[M]. 北京:中国政法大学出版社,2013: 112-113.
[3] 卢亚丽,李艳华,李战国,等. 变限积分函数求导方法研究[J]. 河南教育学院学报:自然科学版,2004, 13(1):4-6.
[4] 钮宏霞. 变限积分求导公式在高维典型立体上的推广[J]. 数学的实践与认识,2008, 38(20): 234-238.
[5] 曲健民,杨高全. 关于积分上限函数的几个定理[J]. 数学理论与应用,2004, 24(4): 47-48.
[责任编辑:熊玉涛]
The Derivation of Single Variable Continuous Functions
XIONG Liang-peng
(School of Engineering Technology, Chengdu University of Technology, Leshan 614007, China)
This paper studies the derivation of single variable continuous functions defined by uncertain limit integrals. Some general derivation formulas and methods for four different cases are given. Furthermore, it demonstrates the importance of these methods by examples.
continuous functions; variable limited functions; definite integrals
O172.1
A
1006-7302(2014)01-0005-05
2013-10-05
熊良鹏(1983—),男,湖北武汉人,讲师,硕士,研究方向为高等数学和几何函数论.
