基于区间三相潮流的配电网故障恢复优化算法

高飞，李红青

(1． 山东省烟台市牟平区供电公司，山东 烟台264100;2． 湖南省湘电试验研究院有限公司，湖南 长沙410007)

我国配电网呈辐射状运行，当出现故障后，不可避免地会出现一些失电区，采取有效的故障恢复策略，减小停电范围，缩短停电时间，是十分必要的。配电网故障恢复算法大致可分为3 类:①传统优化算法，如混合整数优化法〔1－2〕，分支界定法〔3〕;②启发式算法〔4〕;③人工智能算法，如专家系统〔5〕，遗传算法〔6〕等。

文中针对配电网三相参数不对称、三相负荷不平衡及测量终端在实测过程中存在误差而导致的负荷数据不准确的情况，采用区间算法计算三相潮流，比基于单相模型的点迭代更能全面真实地反映电网的状态。采用非线性递减惯性权重的策略，防止算法陷入局部最优，并利用种群适应度方差这一指标判断粒子群算法是否存在早熟现象，可准确地判段出种群可能陷入局部解，并自适应随机选出部分粒子进行变异，使其跳出局部极值，从而达到全局最优。并提出了基于区间三相潮流的故障恢复优化算法。

1 区间三相潮流

1.1 区间数及区间计算

对于原始数据取值为一个区间，或者原始数据不能精确得到，只知道其界限范围的问题，可以通过区间数学〔7〕进行求解，得到该问题的区间解或解所在的范围。

对于任意给定的X ∈I(R)定义以下参数:

中点

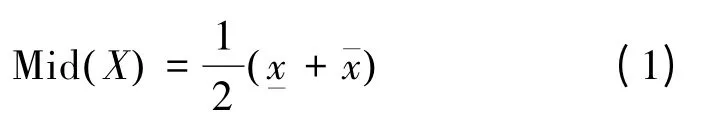
半径

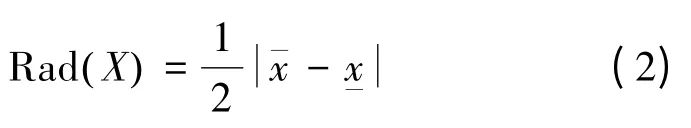
给定区间

定义区间四则运算如下:

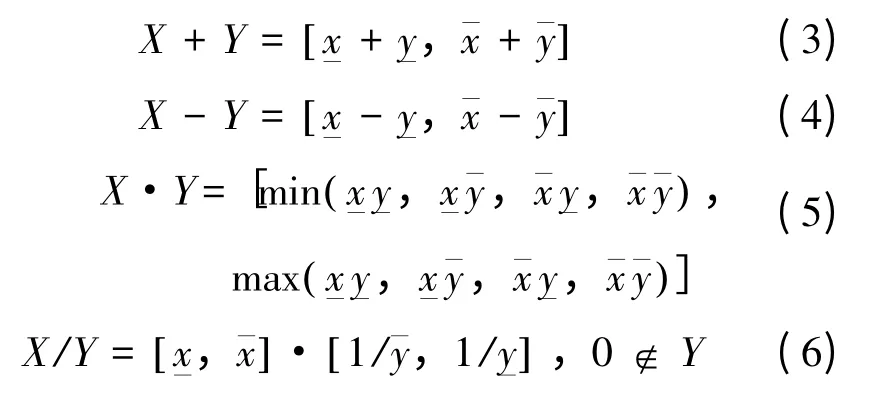
1.2 区间比较

采用区间算法进行故障恢复，目标函数取值也为区间数，因此，需要通过区间比较〔8〕来表征其优化程度。

(2)若Mid(X)＜ Mid(Y)，则称X 拟小于Y，记作X ≺Y;

实际计算结果大多数为拟大于或拟小于的情况，采用下述方法来表示2 个区间相差的程度，即大小关系。

设区间Xi－1和Xi分别为2 次迭代的计算结果，记2 个区间中点的距离di=Mid( Xi－1)－ Mid(Xi)。若di＞0，则表明区间Xi与区间Xi－1相比较优;若di= 0，则比较2 个区间的半径，若Rad Xi()＜Rad( Xi－1)，则区间Xi较优。

为了描述方便，如不加特殊说明，文中所用变量均为代表区间数的变量，所涉及运算采用区间运算。

1.3 配电网三相潮流的区间算法

配电系统三相参数不对称和三相负荷不平衡的特点不能忽略，并且考虑到运行时的不确定因素，采用区间三相潮流算法比传统的基于单相模型的点迭代算法更符合配电网运行的实际情况。

配电网具有闭环设计、开环运行的特点，其基本模块构成如图1 所示。前推回代法计算辐射状配电网潮流计算速度快、收敛性好、存储空间要求低、编程简单。

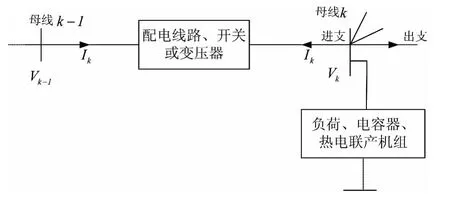
图1 配电网基本模块示意图

因此，文中潮流计算采用前推回推的三相区间算法，计算步骤如下:

(1)建立基于区间算法的配电网三相潮流计算模型〔9〕。

重复步骤(2)，(3)，直至各母线的三相电压矢量的区间上下边界相对于上一次的数值偏差小于设定的阈值。

2 故障恢复模型

2.1 故障恢复目标函数

配电网故障恢复是一个多目标的组合优化问题。常用的目标函数有:网损最小、失电负荷最少、开关操作次数最少以及负荷均衡等。

文中以尽量减小有功网损、失电负荷和开关操作次数为目标建立故障恢复的数学模型。

式中 λ1，λ2，λ3为权重系数，满足λ1+ λ2+ λ3= 1;fP，loss为有功网损目标函数，为区间三相潮流计算得出;fs，out为失电负荷量目标函数;fswitch为开关操作次数目标函数;n 为闭合支路数;k 为支路编号;Ik为流过支路k 的电流;rk为支路k 的电阻;Sout为失电负荷;s 代表开关数，当开关i 状态发生变化时，yi取1，否则取0。

2.2 故障恢复的约束条件

1)辐射状运行的网络约束

式中 gk为当前的网络结构;Gk为所有允许的辐射状网络结构。

2)节点电压约束

3)线路容量约束

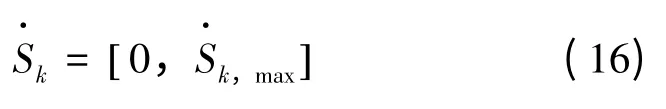
在求解故障恢复模型的过程中，将电压约束和线路容量约束以罚函数的形式加入目标函数中。

3 改进二进制TS-PSO

3.1 粒子群算法

粒子群算法(Particle Swarm Optimization，PSO)是一种基于群体智能的优化算法，由Kennedy 和Eberhart 在1995年提出，源于对鸟类捕食行为的研究。其基本原理是在解空间随机初始化一群粒子，然后各粒子按照某种规率，根据自身和群体所经历的最好位置调整飞行速度和移动，最终达到最优解，被广泛应用于电力系统中。

在配电网故障恢复中应用的主要是二进制粒子群算法(Binary Particle Swarm Optimization，BPSO)。问题的解为粒子的位移，粒子位置的每一维分量被限制为0 或1，对应配电网开关的开、合2 种状态，即粒子的维数等于开关数，目标函数值对应算法的适应度。

假设在D 维搜索空间中，第i 个粒子的位移和速度分别为Xi=(xi1，xi2…xiD)和Vi=(vi1，vi2…viD)，粒子在每次迭代中通过个体极值Pi=(pi1，pi2…piD)和群体极值Pg=(pg1，pg2…pgD)来更新自己的速度和位移，其更新规则如下:

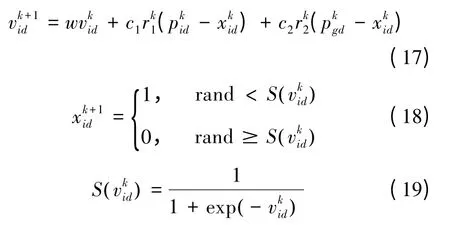
式中 w 为惯性权重;c1，c2为学习因子;r1，r2为［0，1］间的随机数;rand 为［0，1］之间均匀分布的随机数;d = 1，2…，D。

3.2 惯性权重的选择及早熟现象的判定

基本粒子群算法存在早熟收敛的现象，文中对惯性权重采取非线性递减的策略，提高算法跳出局部最优的能力，并采用种群适应度方差〔10〕加以判断，若陷入局部最优，随机选取一部分粒子进行变异，从而保证算法能够得到全局最优解。

1)非线性递减的惯性权重

在算法初期，较大的惯性权重有利于算法全局寻优，而到了算法后期，则需要减小惯性权重值，使算法迅速收敛。采用非线性递减的惯性权重，可以使惯性权重随着迭代次数的增加迅速降低，减小迭代次数，提高搜索速度。因此，文中按照式(20)对惯性权重进行动态调整。

式中 ws和we分别为初始惯性权重和最大迭代次数时的惯性权重，一般取ws=0.95，we=0.4;d1和d2为控制因子，控制惯性权重取值在ws和we之间，取d1=0.2，d2=7;t 为当前迭代次数;tmax为最大迭代次数

2)种群适应度方差δ2

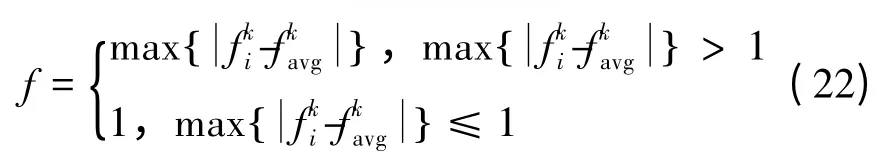
适应度方差δ2反映了群体的收敛程度，在搜索初期，各粒子适应度相差较大，δ2较大，随着迭代次数的增加，粒子个体适应度越来越接近，δ2逐渐变小，当δ2＜δ0(预先设定的阈值)时，认为算法可能陷入局部最优，这时需要对粒子进行变异。

3.3 自适应变异

变异是对粒子的位移重新初始化，为了保证配电网的拓扑约束，利用图论中的避圈法〔12〕生成粒子的位移，使得每次产生的解都是可行解。

当用δ2判断算法陷入早熟收敛时，随机抽取部分粒子进行变异，这种随机过程使种群具有多样性。较大的变异数目能提高种群的多样性，使算法很快地跳出局部最优，在搜索初期有利于全局寻优;但在算法后期，过大的变异数目容易使粒子错过全局最优，算法不易达到收敛，。因此，需要采用式(23)自适应确定变异数目，使整个算法阶段变异过程中粒子变异数目先大后小。

式中 n 为变异数目;N 为种群规模;β1，β2为最小、最大变异系数，可自行设定;K，k 分别为最大迭代次数和当前迭代次数。

4 故障恢复策略

4.1 切负荷策略

若在故障恢复形成辐射状网络之后，仍然存在支路有过载负荷，则需要通过切负荷来满足安全运行约束本文按照供电优先级切除负荷〔13〕。

定义γ(0 ＜γ ≤1)为负荷等级因子，ΔSk为支路k 的越限容量。校验某一供电路径上是否有容量越限，若有越限，则从各分支线路末端开始，切除γ/ΔSk最小的末端负荷，重复上述过程，直至容量不再越限为止;然后校验电压，若某供电路径上出现电压越限，则从各分支线路的末端开始，切除γ·Ui最小的的末端负荷，重复上述过程，直至没有电压越界。

4.2 故障恢复具体步骤

基于区间三相潮流的配电网故障恢复优化算法的步骤如下:

1)初始化。输入配电网络基本电气信息，网络拓扑分信息、负荷信息、故障处理信息和失电区、带电区及故障区的范围等;算法参数初始化，粒子长度、种群规模、惯性因子、学习因子等;

2)生成粒子群算法的初始速度与位移:随机生成初始速度，基于初始速度采用避圈法生成初始位移;

3)基于拓扑识别采用基于前推回代的三相区间算法计算潮流;

4)计算各粒子的适应度，对于每个粒子，将其适应度与其个体极值做比较，若比个体极值优秀则将其更新为个体极值，否则不更新。将当前所有粒子的个体极值与群体极值做比较，若个体极值比群体极值优秀则更新为群体极值，否则不更新，第1 次迭代中将各粒子的初始值作为个体极值，任一粒子作为群体极值;

5)判断是否满足收敛条件，若满足，停止迭代，转至步骤(8)，否则，进行步骤(6);

6)计算种群适应度方差δ2，判断算法是否陷入局部收敛，若δ2＜δ0则自适应随机选取粒子进行变异，转至步骤(3)，否则，进行步骤(7);

7)按照式(17)—(20)更新粒子速度与位移，转至步骤(3);

8)判断是否存在过载线路，若存在，则按供电优先级对过载负荷进行切除，直至过载消除并输出当前解为最优解;若不存在，则输出当前解为最优解。

5 算例分析

文中采用的测试系统如图1 所示，系统的基准电压为12.66 kV，系统总的有负荷为2.71 MW，无功负荷为1.8 Mvar。节点负荷、支路阻抗以及支路最大允许通过的潮流等数据见文献〔14〕。

图2 69 节点配电系统

假设支路5－6 发生故障，则支路4－5 和6－7必须打开，将支路5-6 隔离，因此种群中粒子的长度取为70。

初始化种群规模M 为50，学习因子c1= c2=2.0，最大迭代次数K 取80，目标函数权重λ1=0.1，λ2= 0.5，λ3= 0.4。

为对应文中的区间潮流计算，假定算例给出的各节点负荷数据的误差为±5%，据此将负荷表示为区间值进行计算。

首先，为验证恢复策略的有效性，分别采用未经改进PSO 和本文提出的改进PSO 算法进行仿真验证，对其结果进行比较，见表1。

表1 PSO 和改进PSO 计算结果比较

表1 中，失电负荷为0 表明所得出的故障恢复方案没有线路出现过载，通过与传统PSO 算法的对比可以看出文中提出的基于改进PSO 算法故障恢复算法得出的故障恢复方案能够降低网络损耗，并控制节点电压均衡，能够得到全局最优解。

为验证基于区间三相潮流的故障恢复的合理性，对于改进的PSO 算法，分别采用区间算法和该算例的精确点值计算潮流，仿真结果比较见表2。

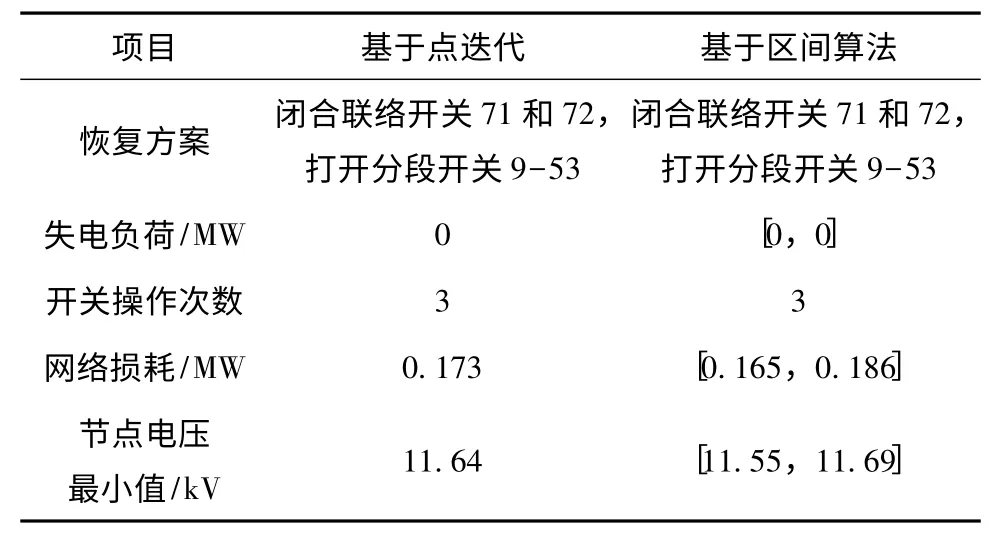
表2 点迭代与区间算法计算结果比较

由表2 可以看出，基于区间潮流计算得到的各指标区间数均包含了基于点迭代潮流计算的结果，说明基于区间三相潮流的故障恢复算法能够包含精确解，并且能够得到正确的故障恢复结果，证明了该算法的合理性。

6 结束语

文章提出了一种基于区间三相潮流的配电网故障恢复算法。首先，针对配电网三相不平衡的特点和在故障时由于不确定因素导致采集到的各个负荷点的实时数据可能会产生的误差，采用区间算法计算三相潮流;其次对基本PSO 算法进行了改进，将模拟退火的思想融入了惯性权重的选择，并利用种群适应度方差这一指标判断算法是否“早熟”，通过自适应变异使算法跳出局部极值;最后通过实际算例验证了文中提出的故障恢复方案的有效性，并更能全面真实地反映电网的状态。

〔1〕K.Aoki，kuwabara，T． Satoh，etc． Outage State Optimal Load Allocation by Automatic Sectionalizing Switches Operation in Distribution Systems〔J〕． IEEE Trans，on PERD，1987(4):1 177-1 185．

〔2〕K.Aoki，T.Satoh，M.Itoh，etc．Voltage Drop Constrained Restoration of Supply by Switch Operation in Distribution Systems〔J〕． IEEE Trans． On PWRD，1988(3):1 267-1 274．

〔3〕J． Nahlman，G． Strbac，A New Algorithm for Service Restoration in Large-Scale Urban Distribution Systems 〔J〕． Electric Power Systems Research，1994，29．

〔4〕林海源，李晓明，余平． 基于支路交换和模拟退火的配电网重构算法〔J〕． 华东电力，2004，32(11):703-707．

〔5〕杨成峰，乐秀璠． 配电网故障恢复专家系统的一种实现〔J〕．电力自动化设备，2001，21(11):91-94．

〔6〕蒋勇斌，崔浩，袁晓明． 基于遗传算法的配电网故障恢复模型研究〔J〕． 华东电力，2012，40(12):2 234-2 237．

〔7〕王德人，张连生，邓乃扬． 非线性方程的区间算法〔M〕． 上海:上海科技出版社，1986．

〔8〕李锦． 基于区间负荷的配电网重构研究〔D〕． 天津:天津大学，2011．

〔9〕王守相，王成山． 基于区间算法的配电网三相潮流计算模型〔J〕． 中国电机工程学报，2002，22(2):52-58．

〔10〕贾松卫，高岳林． 融合模拟退火和混沌的混合粒子群算法〔J〕． 计算机工程与应用，2009，45(7):52-55．

〔11〕Gao Yue-lin，Duan Yu-hong．An adaptive particle swarm optimization algorithm with new random inertia weight〔C〕//Communications in Computer and Information Science，2007，8:342-350．

〔12〕王朝瑞． 图论〔M〕． 北京:北京理工大学出版社，1997．

〔13〕康巍晶，刘伟，李海城． 配电网恢复控制的研究〔J〕． 继电器，2005，33(21):41-44．

〔14〕SAVIER J S，DAS D． Impact of network reconfiguration on ;oss allocation of radial distribution systems〔J〕． IEEE Trans on Power Delivery，2007，22(4):2 473-2 480．