一种航迹网络图粒子群优化生成方法＊

黄自强 蔡 超 孙希霞

（华中科技大学自动化学院多谱信息处理技术国防科技重点实验室 武汉 430074）

1 引言

飞行器航迹规划是在综合考虑飞行器到达时间、燃料消耗、威胁以及特定飞行区域等因素的前提下，为飞行器规划出一条最优，或者是较满意的飞行航迹，以保证圆满完成飞行任务［1］。在现代战争中，由于战场环境的动态变化以及任务的不确定性，飞行器的航迹规划空间往往非常大，规划算法非常耗时，无法满足在线实时规划的要求。有研究者根据高速公路网规划的思想，提出了基于网络图的分阶段航迹规划方法［2～6］。第一步，在预处理阶段构造满足一系列约束条件的航迹片段，这些航迹片段构成网络图。第二步，给定规划任务，利用网络图搜索出一条从指定发射点到目标点的航迹。这样路径规划问题被转化为一个网络图的搜索问题。这种方法大幅缩减了航迹规划过程的搜索量，从而加快了规划速度，能满足在线实时规划的要求。类似的方法还有通视图法、随机路线图法等［7～11］。通视图是由规划空间中的障碍物的相互可见的顶点间的连线构成。通视图可用于求解二维规划空间中的最短路径问题，尽管它可用于高维规划空间，但此时生成的路径将不再是最短的。另外，通视图不能表达物体运动的方向性约束，这样使得生成网络图可行解较少。随机路线图法是一种针对多自由度问题的路径规划方法。该方法在规划空间中随机进行采样生成路线图，然后在该路线图中搜索路径。该方法的优点之一就是可以在规划时间和路径的质量之间进行权衡，构造随机路线图的时间越长，得到最优路径的可能性就越大。在确定环境下，随机路线图一般可以事先构造。

已有的航迹网络图生成方法并没有考虑网络图的最优性，包括：1）空间覆盖能力；2）网络图总体代价最优性；3）重组航迹的最优性等。

本文利用粒子群优化算法优化网络图节点的分布，使航迹网络图整体代价较优，重组航迹也较优。

2 航迹网络图及其优化问题

航迹网络图是由网络节点和节点间的航迹片段构成如图1所示。航迹网络图的构建过程，首先是对规划空间进行等网格划分，将规划空间划分为一个个相互毗邻的网格。多个较小的网格又可以形成一个较大的网格，这样实现了多尺度网格的划分。在每个网格内，在匹配区内随机选取节点。然后根据飞行器飞行约束、环境约束等约束条件进行节点间的航迹片段规划。其规划结果就构成了一幅初始的航迹网络图。航迹网络图可以表示为G＝（V，E），其中V为图中节点的集合，E为航迹片段（图G中的边）的集合，节点具有八个飞行方向（由匹配区导航点的性质决定），空间位置由坐标（x，y，z）表示。

图1 网络节点及小尺度航迹片段

航迹网络图主要受规划空间、网格大小、节点分布以及航迹片段生成算法等因素的影响。在规划空间、网格大小和航迹片段生成算法都已确定的情况下，节点位置的改变会造成航迹网络图空间分布的较大改变，相应的航迹网络总体代价也会有较大的改变。这里，我们用航迹网络图中所有航迹片段代价的和来表示网络图的总体代价，航迹片段的代价考虑航迹长度、高度、转弯次数、威胁等因素。

航迹网络图的优化，除了考虑网络图的代价因素外，还要考虑网络的密集程度，规划空间的覆盖能力，分布均匀性等。

网格的划分决定了航迹网络的密集程度。航迹片段规划算法采用A＊搜索算法，在满足给定约束条件的情况下，A＊算法能够规划出节点间的最小代价航迹片段。改变航迹网络节点位置，将影响航迹片段经过的空间位置及代价大小，相应地改变航迹网络的总体代价和空间覆盖能力。

结合上述分析，本文设计出一种通过求解航迹网络节点最优分布进而获得最优航迹网络的优化方法。

3 基于粒子群算法的网络图优化

3.1 粒子群算法原理

粒子群算法是基于群体的演化算法，其思想来源是人工生命和演化计算理论。由于其简单、有效的特点，可以用于复杂高维问题的求解，已得到众多学者的重视［7］。在粒子群算法中，每个粒子在搜索空间中的位置代表了所求问题的一个解。每个粒子还有一个速度，来决定它们移动的方向和位置。每个粒子通过优化函数决定了它当前的适应值。粒子群算法初始化为一群随机的粒子，然后通过迭代找到最优解，在每一次迭代中，粒子通过两个“极值”来更新自己的位置和速度。其中，第一个“极值”是粒子本身所找到的最好解（个体极值pbest）；另一个“极值”是整个种群目前所找到的最好的解（全局极值点gbest）［12～15］。粒子更新位置和速度的公式如下：

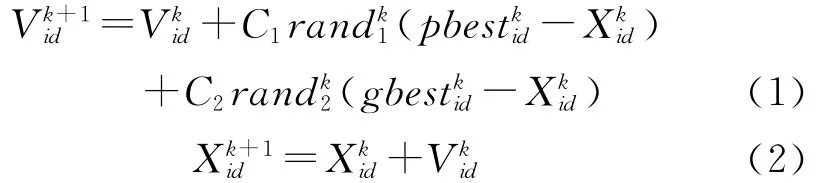
其中，是粒子i在第k次迭代中第d维的速度。C1、C2是加速系数（学习因子）表示每个粒子飞向pbest和gbest位置的随机加速项的权重。合适的值可以加快收敛不易陷入局部最优。一般取C1＝C2＝2。rand1和rand2是［0，1］之间的随机数。粒子i的位置用D维向量Xi＝（xi1，xi2，…，xiD）T来表示，速度为Vi＝（vi1，vi2，…，viD）T。

算法流程如下：

1）初始化。以随机的方式产生出每一个粒子的初始位置与速度。

2）评价每一个粒子。根据适应度函数计算出粒子当前的适应值，并更新个体和全局极值。

3）粒子的更新。用式（1）和式（2）对每一个粒子的速度和位置进行更新。

4）检验是否符合结束条件。如果当前的迭代次数达到了预先设定的最大次数或最小错误要求，则停止迭代，输出最优解。否则转到步骤2）。

利用粒子群优化算法获得优化航迹网络需要解决粒子位置坐标与航迹网络空间分布的对应关系问题，还需要解决粒子适应度函数与航迹网络代价的关系。下面将分别进行讨论。

3.2 基于粒子群算法的航迹网络图优化

航迹网络图的优化有其特殊性。第一，航迹片段的代价是由航迹规划算法中的评价函数确定的。节点发生改变时，航迹片段的代价值往往没有明确的变化趋向。相应地，代价值的变化给出的节点变化引导往往也是不可靠的。换句话说，代价值的变化与节点的变化没有明确的关联。而航迹片段的代价值是优化函数的主要变量，这就造成了优化函数值影响因素的复杂性问题。第二，网络图往往含有大量的节点，任意一个节点的改变都会造成网络图的改变，进而对网络图的优劣产生影响。因此网络图的优化是一个高维复杂优化问题。

采用经典的数学规划方法解决此问题时，必须在精度和求解效率间做某种折中。其中，线性规划法计算速度快，但将该模型线性化存在困难；非线性规划法可以较精确地计及模型的非线性，但一般要求目标函数连续可导，且定义于凸可行域；动态规划法对目标函数无严格限制，容易计及约束条件，但对于高维问题将面临维数灾难。而人工智能算法为求解这类问题提供了新的思路。其中，粒子群优化算法简单、有效，依赖的经验参数少，可以求解复杂的高维非线性函数优化。

基于粒子群算法的网络图优化是通过调整网络图中节点的分布，使网络图的代价降低同时保持网络图的丰富性。当网络图中的节点位置改变时，网络图中的航迹片段需重新生成，进而形成一个新的航迹网络图。这类似于粒子群优化算法中的粒子从一个位置移动到另一个位置。粒子通过相互引导向最优值靠拢，多个网络图之间也可以相互引导，从而使网络图向最优的网络图靠拢。因此可以将网络图看作一个粒子，应用粒子群优化算法求解网络图的优化问题。

将网络图看作一个粒子，每个节点坐标p作为粒子坐标Q的一个分量。则粒子的坐标标为：Qk＝（，，，…，，）T由第k张航迹网络图中所有节点坐标构成，其中N为节点个数。（xj，yj）为航迹网络中第j个节点pj的坐标，1≤j≤N。构造如下目标函数：

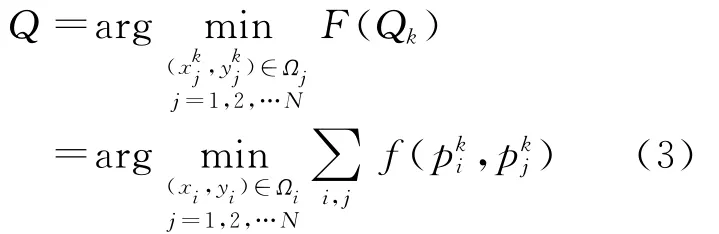
其中f（，）为节点间对应的航迹片段的代价，由航迹片段规划算法求得。如果之间没有规划出可行航迹，则定义f）为一个惩罚常量值，以使节点朝向能规划出航迹的方向移动。Ωj为第j个网格包含的区域，表示限定第j个节点的位置落在第j个网格内，该限定的目的是航迹网络的节点的分布比较均匀，避免过度集中和过度稀疏的情况发生。

实现过程中，Ωj是一个正方形网格。在网络图中，设定节点坐标表示为pj＝（xj，yj），1≪j≪N。由于节点限制在正方形网格内，节点坐标满足：

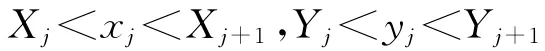
Xj、Xj＋1为节点pj所在网格的竖直方向边界的横坐标。Yj、Yj＋1为节点pj所在网格的水平方向边界的纵坐标。粒子的速度Vk为

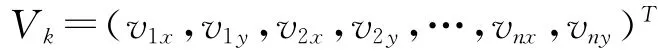
vjx、vjy分别为节点pj＝（xj，yj）的x和y方向上的运动速度。粒子每一维速度限定在一定范围内，满足约束条件：

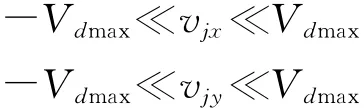
调整Vdmax可以限定粒子的运动速度。如果粒子速度过大，可能会飞跃最优解；粒子速度太小，则容易陷入局部最优。

在优化模型的目标函数中，惩罚代价可以根据航迹片段的数目以及片段的平均代价来设定：

其中，fave为已生成的航迹片段的平均代价，α为惩罚系数，nall为理论上网络图能够生成的航迹片段数，nr为实际生成的航迹片段数。nall取值与节点个数和网格尺度有关。节点个数越多，nall值就越大；反之，就越小。惩罚代价与航迹片段数目成反比：当节点个数和网格尺度确定时，实际生成的片段数nr越大，惩罚代价就越小，否则惩罚代价越大。

因此，两节点间的代价函数定义为

基于粒子群算法的网络图优化流程：

1）初始化种群。以随机的方式产生出每一个粒子的初始位置与速度。若有匹配区限制，则节点必须分布在匹配区上。

2）生成航迹片段。对每个粒子，利用A＊算法生成航迹片段，从而生成航迹网络图。

3）求得适应度值。根据式（3）求得每个粒子当前的适应度值，并更新个体和全局极值。

4）更新粒子位置和速度。根据新得到的个体和全局极值更新粒子的位置和速度。判断每个粒子中节点是否满足网格边界约束和匹配区约束条件。若节点不满足约束条件，则调整节点使其满足约束条件。

5）检验是否符合结束条件。如果达到了预先设定的最大迭代次数或最小错误要求，则停止迭代，输出最优解。否则转到步骤2）。

算法流程图：

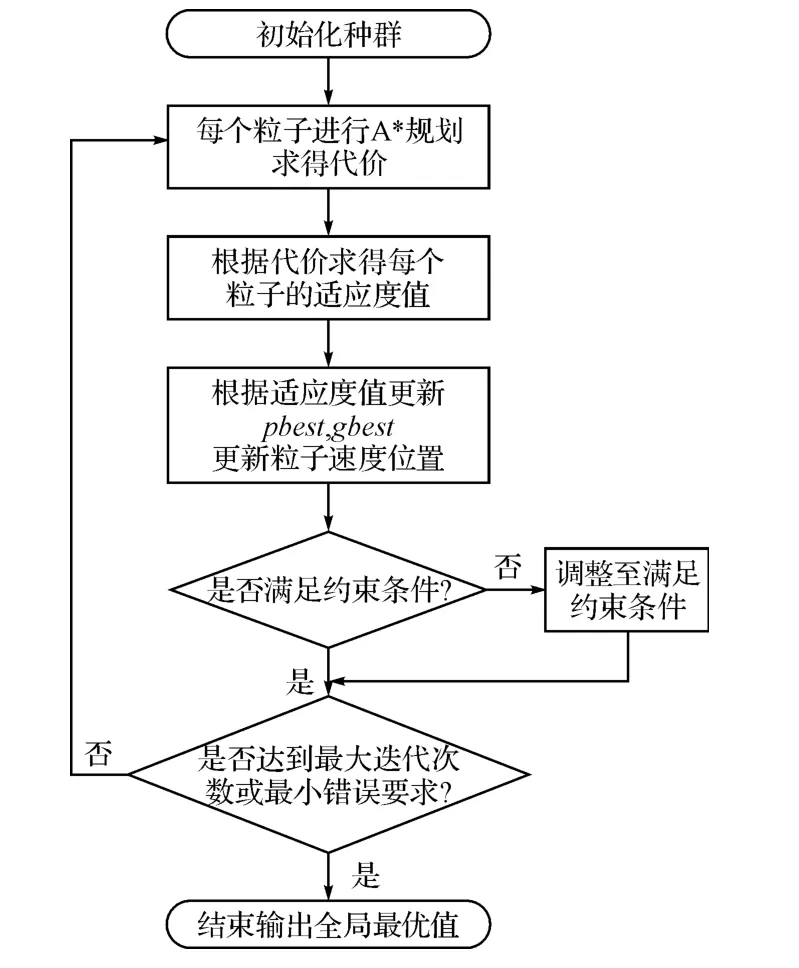
图2 粒子群算法优化网络图的流程图

算法初始化中，在每个网格内随机生成一个节点，并判断节点是否在匹配区上，若在匹配区上，则节点位置确定；否则在网格内按一定策略逐点搜索匹配区。若找到匹配区则节点确定，否则该网格内不设定节点，粒子在该节点对应的分量上不予考虑。所有的节点生成后，利用A＊算法规划出航迹片段。按式（3）求取各粒子个体最优值的初值，其中所有粒子适应度值的最小值为全局最优值的初值。

在航迹网络图的优化过程中，节点必须满足网格边界约束和匹配区约束条件。在每一次迭代过程中，节点移动后，可能移动到相邻网格或超出规划空间，也有可能不在匹配区上。这时必须对不满足约束条件的节点进行调整。当节点不满足网格边界约束时，将该节点置于节点运动路线与网格边界的交点处，并将其速度反向。这样处理可使粒子尽早脱离“非法区域”，尽可能多地探索合理的规划空间。当节点不满足匹配区约束时，调整策略是让节点从当前位置沿着移动方向v逐点探索直到找到匹配区。若按上述方式搜索至网格边界仍未找到匹配区，则使节点从当前位置逐点回退，运动方向为－v，直到找到匹配区。由于粒子的初始位置是在匹配区上，故回退一定能够找到匹配区。这种调整策略能确保粒子在移动过程中的两个“极值”对粒子运动的引导性不变。

4 试验结果与分析

本文给出的算法在6000×6000像素的数字地形高程图上实验，其中，每个像素代表的实际距离是90m。实验中，网格的大小为500×500像素，考虑匹配区限制。粒子群算法的参数设定为：粒子个数，迭代次数90次，粒子每一维的最大速度Vmax＝200，加权系数C1＝C2＝2。本文进行两类实验：先对同一幅初始航迹网络图进行三组粒子群优化实验，然后在优化前后的航迹网络图上进行航迹重组的对比实验。

图3所示是航迹网络图代价的变化情况。从图中可以看出，航迹网络的代价是震荡下降的，这是由优化函数值的影响因素比较复杂造成的。这也会造成算法的收敛精度不高，使得曲线最终在收敛值附近波动。迭代开始时，粒子的代价从1487.25开始快速下降，之后下降趋势逐渐减缓，最后稳定地在1430附近波动。表明该算法能有效地优化网络图的代价。图4是优化后的航迹片段网络图，从中可以看出网络图能够比较均匀地覆盖规划空间，并且网络图中片段也很丰富。

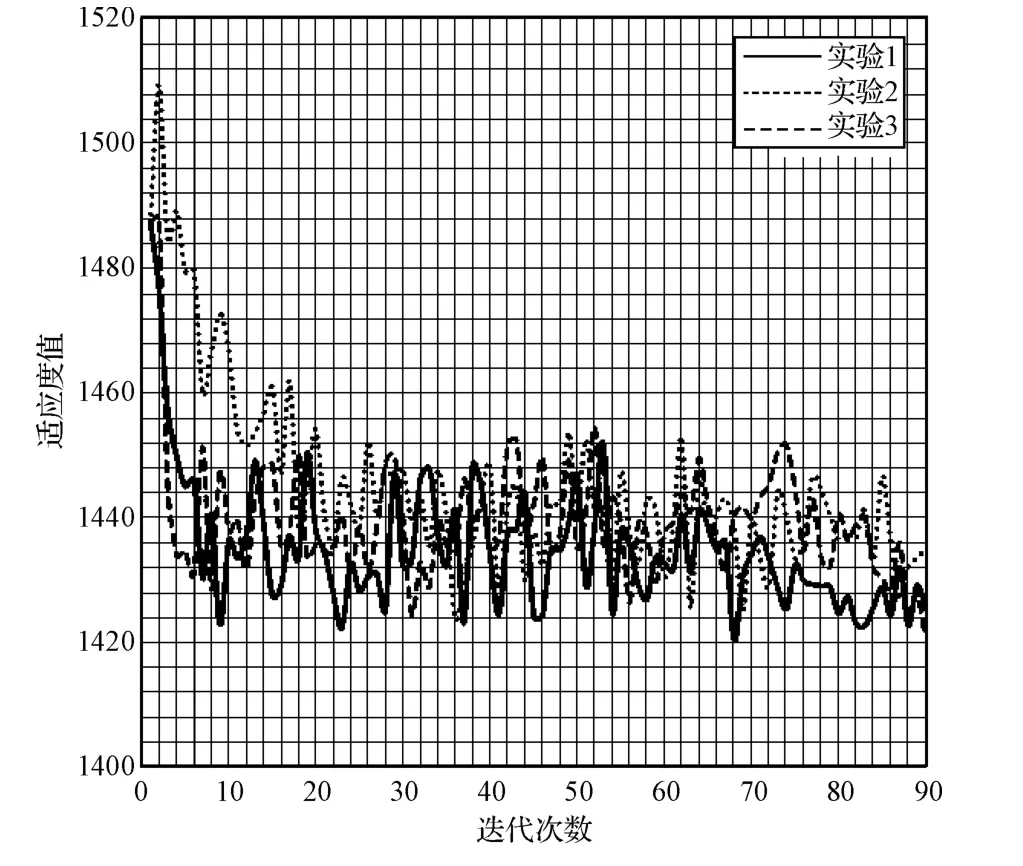
图3 粒子群优化代价变化

图5是在给定同一组发射点和目标点的条件下，在经粒子群算法优化的航迹网络和没有优化的航迹网络上重组出的航迹对比。从图中可以看出，在优化过的网络图上重组得到的航迹比较平滑。表1记录的是进行6次不同任务得到的航迹的长度、水平转弯次数、垂直机动次数的对比结果。其中，任务1是图5中这两条航迹的相关参数的对比。

图4 优化后的网络图

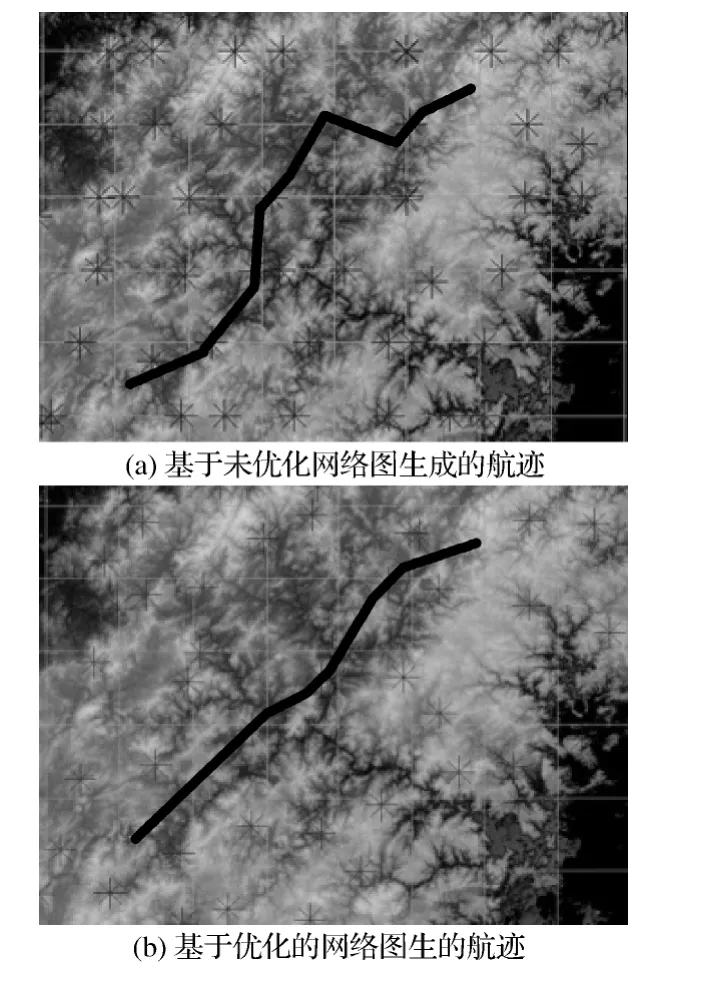
图5 网络图优化前后重组出的航迹

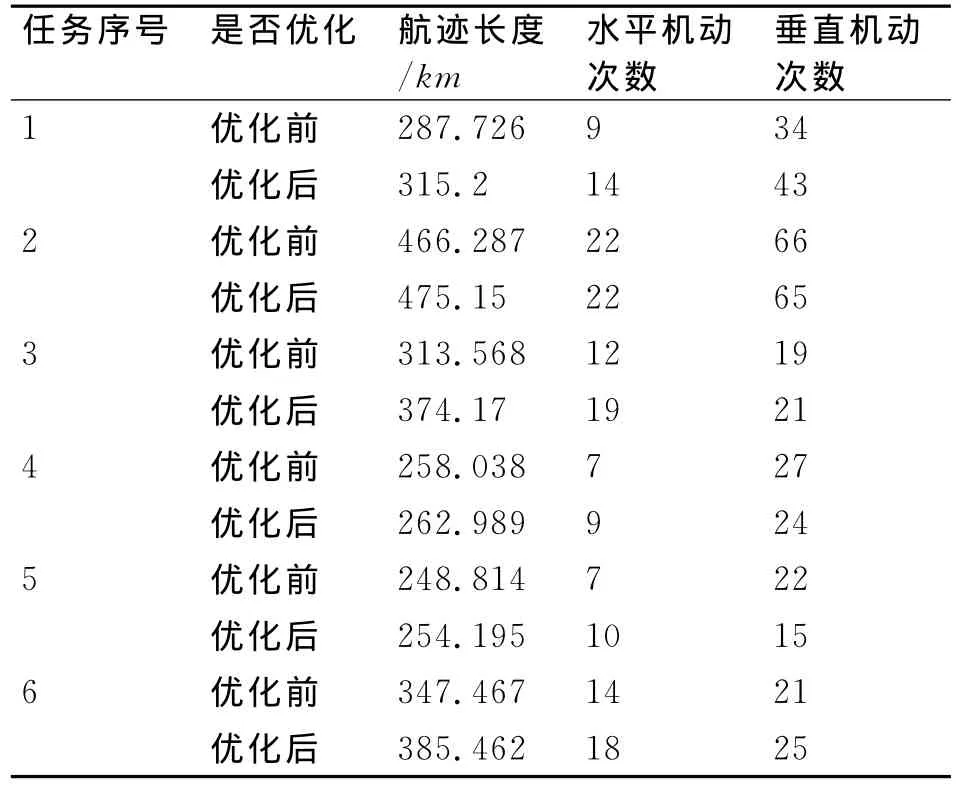
表1 航迹相关参数的对比

任务1中，基于优化的网络图重组的航迹长度为287.726km，较基于未优化的网络图重组的航迹长度315.2km短。在水平机动次数上的对比是9次低于14次。在垂直机动的次数上的对比是34次低于43次。从表1可以看出，每组任务中，左边的航迹长度均比右边的航迹长度短，水平机动次数少。在垂直机动次数上，左边的航迹在大多数情况下要优于右边的航迹。在统计意义上，基于较优的网络图重组出的航迹要优于基于未优化的航迹网络图重组出的航迹。

5 结语

航迹网络图的优化存在优化函数值影响因素的复杂性问题。并且网络节点通常较多，使得网络图的优化是一个高维复杂优化问题。实验结果表明，本文提出的方法能生成代价较优、片段丰富的航迹网络图。在统计意义上，优化后航迹网络图重组出的航迹要优于优化前网络图重组出的航迹。

航迹网络图优化的后续研究，可以在进一步提高优化效率等方面展开。

［1］郑昌文，严平，丁明跃，等.飞行器航迹规划研究现状与趋势［J］.宇航学报，2007，28（6）：1441－1446.

［2］Li ShiDong，Ding Mingyue，Cai Chao.A novel path planning method based on path network［C］／／Proceedings of the SPIE 6thInternational Symposium on Multispectral Image Processing and Pattern Recognition，2009.

［3］Li S，Ding M，Cai C，et al.Fast online path planning method based on path network［C］／／Computer Application and System Modeling（ICCASM），2010International Conference on.IEEE，2010，10：V10－224－V10－227.

［4］Li S，Ding M，Cai C.Path planning using FMM with direction and curvature constrained［C］／／Sixth International Symposium on Multispectral Image Processing and Pattern Recognition.International Society for Optics and Photonics，2009：749847－749847－8.

［5］Changuien Z，Mingyue D，Chengping Z.An evolutionary real－time 3Droute planner for aircraft［J］.Systems Engineering and Electronics，Journal of，2003，14（1）：47－53.

［6］Li S，Ding M，Cai C.A new roadmap constitution method based on fividing grid and level－set［C］／／Intelligence Information Processing and Trusted Computing（IPTC），2010International Symposium on.IEEE，2010：647－650.

［7］Kavraki L E，Svestka P，Latombe J C，et al.Probabilistic roadmaps for path planning in high－dimensional configuration spaces［J］.Robotics and Automation，IEEE Transactions on，1996，12（4）：566－580.

［8］Kavraki L E，Kolountzakis M N，Latombe J C.Analysis of probabilistic roadmaps for path planning［J］.Robotics and Automation，IEEE Transactions on，1998，14（1）：166－171.

［9］Siméon T，Laumond J P，Nissoux C.Visibility－based probabilistic roadmaps for motion planning［J］.Advanced Robotics，2000，14（6）：477－493.

［10］Nissoux C，Siméon T，Laumond J P.Visibility based probabilistic roadmaps［C］／／Intelligent Robots and Systems，1999.IROS'99.Proceedings.1999IEEE／RSJ International Conference on.IEEE，1999，3：1316－1321.

［11］Lulu L，Elnagar A.A comparative study between visibility－based roadmap path planning algorithms［C］／／Intelligent Robots and Systems，2005.（IROS 2005）.2005IEEE／RSJ International Conference on.IEEE，2005：3263－3268.

［12］Kennedy J，Eberhart R C.Particle swarm optimization［C］／／Proceedings of IEEE International Conference on Neutral Networks，Perth，Australia，1995：1942－1984.

［13］Shi Y H，Eberhart R C.A modified particle swarm optimizer［C］／／IEEE International Conference of Evolutionary Computation，Anchorage，Alaska， May 1998.

［14］Shi Y H，Eberhart R C.Parameter selection in particle swarm optimization［C］／／Annual，1998.

［15］Clerc M，Kennedy J.The particle swarm－explosion，stability，and convergence in a multidimensional complex space［J］.Evolutionary Computation，IEEE Transactions on，2002，6（1）：58－73.