基于多变量内模解耦的CFB锅炉燃烧控制研究
2014-07-10钟亮民刘吉臻王瑞琪
钟亮民, 刘吉臻, 张 恒, 王瑞琪
(华北电力大学 控制与计算机工程学院,新能源电力系统国家重点实验室,北京102206)
循环流化床(CFB)锅炉作为传统火力发电技术的重要和有益补充,近年来越来越受到重视.高参数、大容量的超临界CFB锅炉机组正处在试点实践过程中.但无论参数和容量如何变化,CFB锅炉的自动控制问题始终是重点和难点.CFB锅炉是一个集流动、传热和燃烧等诸多过程于一体的复杂系统,其控制对象具有多参数、非线性、大滞后、大惯性和多变量紧密耦合的特点,部分控制对象还有右半平面(RHP)零点,具有反向响应特点.这些特点给CFB锅炉燃烧系统的自动控制带来很大困难.CFB锅炉燃烧控制的目的是维持稳定的主蒸汽压力并保持一定的床温.通常选取一次风量-床温和给煤量-主蒸汽压力作为主控制通道,但这两者之间存在强耦合,且主通道和干扰通道的对象特性差别很大,解耦是必要且困难的,即使是超临界CFB锅炉,解耦也依然是首要任务[1].
内模控制(IMC)因其鲁棒性强、设计和整定简单明了等特点而受到关注.王东风等[2]先对对象进行补偿解耦,使之成为对角阵或者对角占优矩阵,然后对广义对象进行内模控制.JIN Qibing等[3]提出的基于V规范型对象预补偿解耦方式是对文献[2]中方法的发展.杨锡运等[4]提出主通道解耦,将其余通道看做是干扰通道.比较常用的是 Wang等[5]提出的解析解耦算法,该控制器兼具解耦和控制的作用.周平等[6]在文献[5]方法的基础上提出优化实际工业过程运行的解耦措施.Chen等[7]将内模控制用于Smith迟延补偿控制器的设计,并应用于一阶迟延多变量非方系统中.靳其兵等[8]从解耦和零稳态误差两方面入手,考虑系统稳态值,避免了模型降阶的问题,简化了迟延问题的处理.
笔者针对CFB锅炉燃烧控制系统主蒸汽压力和床温的强耦合性、大惯性和大迟延的特点,采用多变量内模控制,通过解析的代数方法,使由于模型求逆而产生的预测项和不稳定极点得到补偿.在设计过程中通过对迟延项的适当逼近措施和次最优降阶方法的使用,使得控制器便于工业实现.设计滤波器将控制器中的闭环缓慢极点或主导极点抵消,使系统响应加快并能够有效改善响应性能.滤波器时间常数的整定采用对控制量与输出值的瞬时性能指标(调节时间和超调量)线性求和来衡量.在该优化条件下,进行系统的输入扰动、输出扰动响应,并对模型匹配和失配情况下系统的鲁棒性进行验证.
1 对象提出
马素霞等[9]通过对75t/h CFB锅炉进行机理分析并建立数学模型,研究其燃烧系统的动态特性,给出在70%~110%负荷下CFB锅炉多输入多输出(MIMO)燃烧系统的传递函数矩阵.笔者选取主蒸汽压力和床温这对强耦合变量所构成的2×2矩阵作为研究对象.给煤量同时影响控制系统的很多重要参数,对主蒸汽压力、床温和烟气含氧量的影响尤其明显,给煤量突然增加会使主蒸汽压力和床温升高而烟气含氧量降低.床温的控制是通过调节一次风量来实现的,一次风量对燃烧起着主导作用,其作用是维系炉内和分离器内的物料循环流化,提供燃料燃烧的大部分氧气.一次风量的相对稳定对CFB锅炉的安全稳定运行至关重要.
一般认为,给煤量的变化首先将引起床温的变化,由于CFB锅炉内部蓄热量很大,所以床温的变化有较大迟延,而炉内工质温差的存在则造成炉内传热状况发生改变,于是主蒸汽压力也随之改变.本文除特殊说明外,床温均指密相区床料温度.控制床温的目的是保持炉体内密相区床温在850~950°C最佳流化温度区间内.当通过改变一次风量调节床温时,床温的反应迅速,几乎没有迟延.但一次风量调整幅度与其对炉内物料流化的影响正相关,因此将引起主蒸汽压力的波动.另外,最小流化风量是一次风量的下限.考虑解耦的燃烧系统控制结构框图见图1.
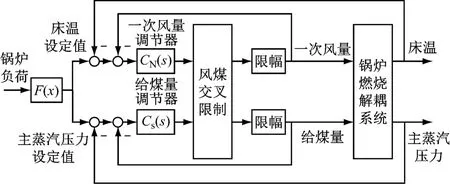
图1 考虑解耦的燃烧系统控制结构图Fig.1 Structural diagram of the combustion control system considering decoupling
根据文献[9]的阶跃拟合关系,该燃烧系统动态特性可描述为
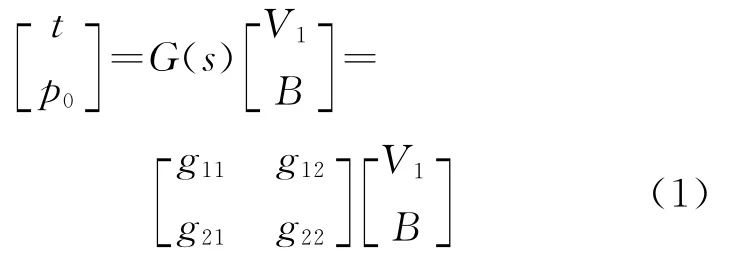
式中:t为床温,℃;p0为主蒸汽压力,MPa;V1为一次风量,m3/h;B 为给煤量,kg/h;d1为系统输入扰动量;d2为系统输出扰动量;G(s)为控制通道传递函数矩阵.
G(s)的组成为
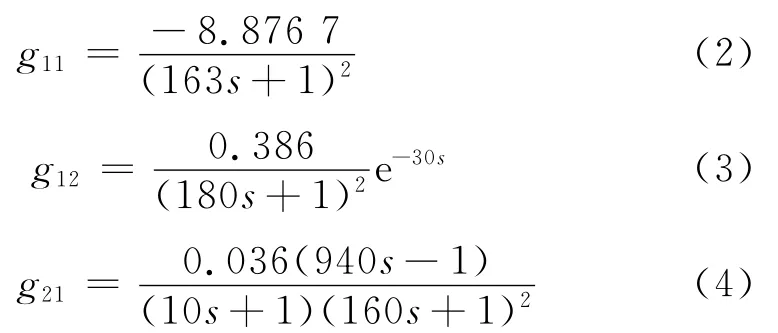

由式(2)~式(5)可见,有些对象为阶数大于2的高阶对象,同时还含有RHP零点.对该两输入两输出(TITO)系统作阶跃响应,可反映出每一条控制通道对象的惯性大、自平衡时间长的特点.由于RHP零点的存在,一次风量变化对主蒸汽压力的影响有逆向响应特性.2个通道均存在耦合,相对增益矩阵为
根据控制理论,当通道的相对增益λij<0.7或λij>1.3时,表明系统存在严重耦合,需要进行解耦设计.在工业中,控制对象以上特点的综合是传统PID控制器难以胜任的.
2 多变量内模控制器的设计
与传统反馈控制相比,内模控制的主要优点是容易获取良好的动态响应,同时能兼顾稳定性和鲁棒性.内模控制系统结构框图见图2.其中,G(s)是系统实际过程对象,一般不能确切得知;G^(s)是对象的过程模型;d1(s)是输入扰动;d2(s)是输出扰动;C(s)是内模解耦控制器;E(s)为模型失配时的系统偏差;u是控制器输出量;r和y分别是系统设定值和输出值.不同于单输入单输出(SISO)系统,在MIMO系统中,G(s)、G^(s)和C(s)均为矩阵,各输入输出均为向量.
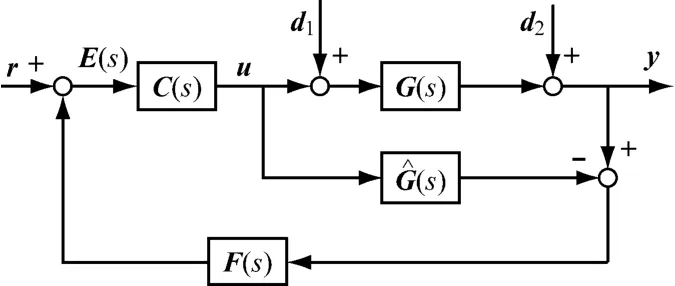
图2 内模控制结构框图Fig.2 Structural diagram of the IMC system
2.1 最优控制器设计
按照常规内模控制器设计二步法,由图2可得系统闭环传递函数H为
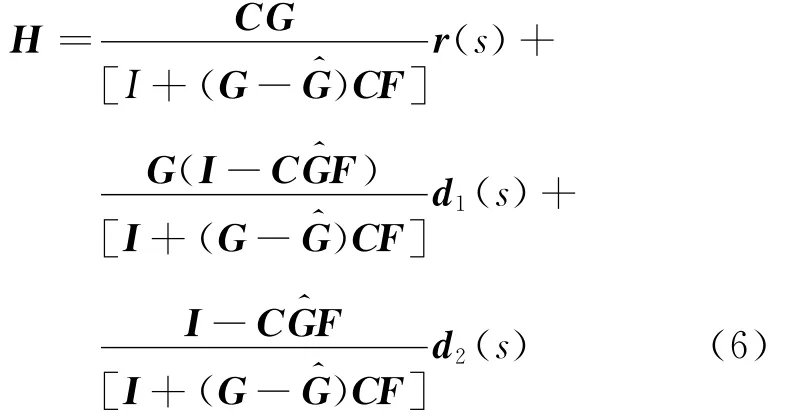
首先设定系统为标称情况,即G(s)=G^(s).不考虑扰动有H=CG.对于如本文中各控制通道均稳定的对象,系统稳定的充要条件是C稳定.易知,最优解耦控制器为

由于绝大多数工业对象都含有迟延,有些还含有RHP零点,因此由式(7)得到的控制器具有预测项,在实际工业过程中无法实现.而RHP极点则使系统不稳定.在推导中,通常将过程对象分解为全通部分(all-pass)和最小相位部分,如
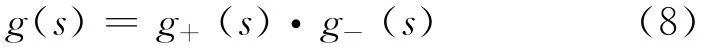
式中:g+(s)包含所有的时滞项和RHP零点;g-(s)是对象稳定最小相位部分.
在此基础上,为使控制器在阶次上能够实现,同时保证模型失配时的鲁棒性,在控制通道上增加一个低通滤波器f(s),则内模控制器为
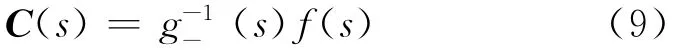
许多文献指出,为进一步增加对模型误差的鲁棒性,可以在反馈回路上再增加反馈滤波器F(s).一般以F(s)=I为单自由度控制,否则为二自由度控制.对于迟延对象的二自由度控制,F(s)的时间常数通常取通道迟延时间的一半[10].
对含有迟延和RHP零点的多变量对象模型传递函数矩阵进行类似分解过程称为内外分解.一般的数值内外分解方法[11]对含迟延项矩阵的分解能力还有待研究.文献[5]中提出的方法计算量较大.Zhang等改进了最优解耦控制器的代数设计过程,通过添加补偿项来消除设计中包含的不可实现和不稳定因素[12-13].考虑如下稳定的、同时含有不同时滞项和 RHP零点的2×2对象模型矩阵G^(s).G^(s)的形式如下
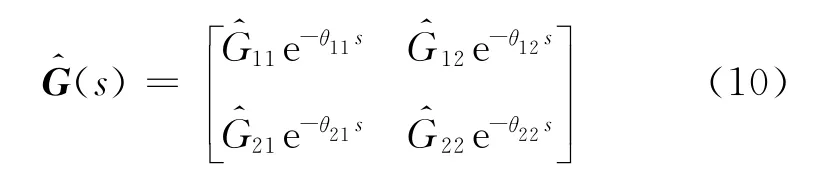
对象模型分解为非最小和最小相位的结果为
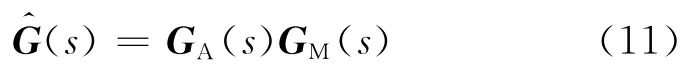
式中:GA为非最小相位部分;GM为最小相位部分;的逆矩阵存在,为
显然,最优解耦控制器为
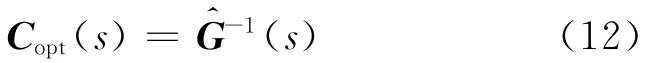
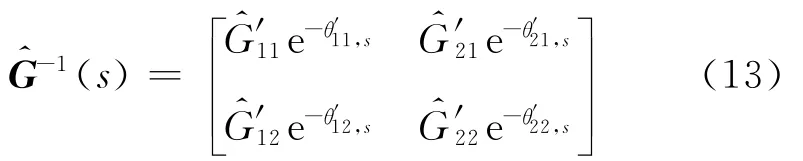
首先处理迟延项.将式(12)等式右边乘以GD(s),GD(s)的形式为
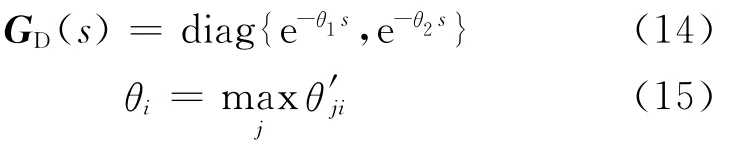
即θi是中第i列的最大迟延项.由此可知所选取的GD(s)可以抵消模型逆中的预测项,并且是唯一的.令相乘结果为则新的控制器为

需要指出,相比SISO系统,由于RHP零点的存在必然导致不稳定极点的出现,在MIMO系统中,对象元素有公共零点时才一定成立.对于任意一个被控对象,当进行到
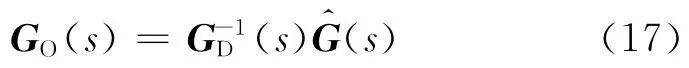
由于GD(s)为仅含时滞项的对角矩阵,不对G^(s)的零极点分布产生影响.因此,
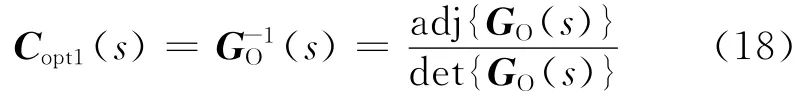
其中det{GO(s)}可能使某些元素不稳定.对于这些不稳定极点,将式(16)等式右边乘以GN(s),使所有RHP极点被抵消,GN(s)的形式如下
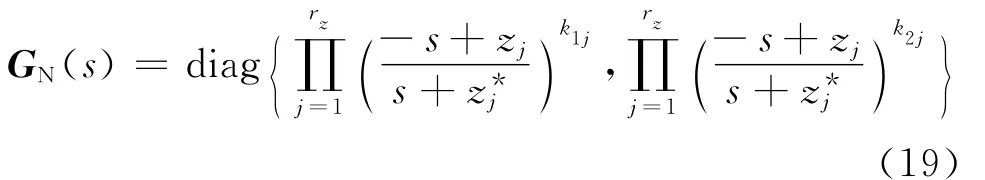
其中zj(j=1,2,…,rz)是(s)中第j列元素RHP极点因式的最小公因式的各个极点.此时,
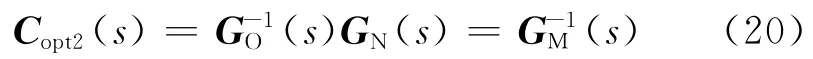
于是便得到了内模控制器Copt2(s).易知,
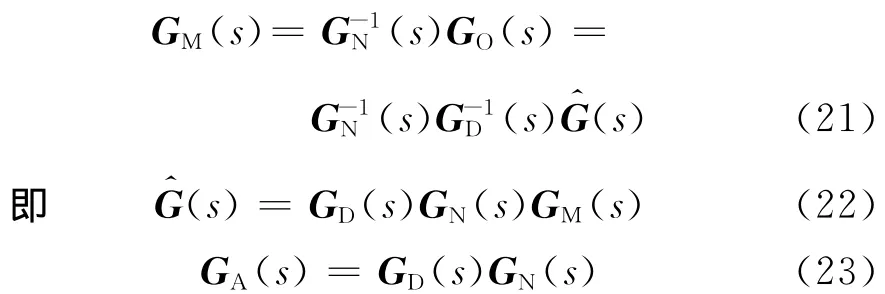
需要指出的是,解耦的完成是以可能引入更多的迟延项或者引入更多的RHP零点到控制器中为代价的.
2.2 滤波器设计
为柔化控制作用和平滑输出响应的作用而引入的滤波器f(s)的形式一般为
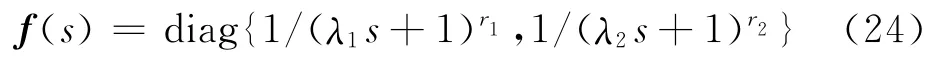
式中:r1、r2的取值使控制器可实现即可;λ1、λ2为滤波器的时间常数,是控制器中唯一可调的参数,其取值是系统响应快速性与鲁棒性的折中.
Horn等[14]通过在滤波器分子上引入可调参数抵消被控过程中(对象)的缓慢极点,以加强抗负荷扰动的能力.改进滤波器的形式如下
类型1
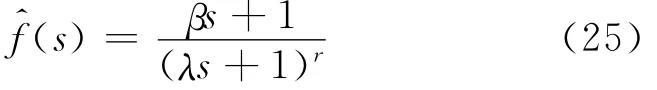
类型2
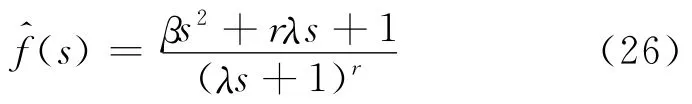
文献[14]要在实现零极点抵消的同时,λ、β的值唯一确定,因此无法对输出响应性能进行调节.受此启发,笔者引入如下类似的滤波器矩阵
类型1
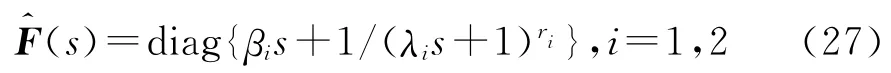
类型2
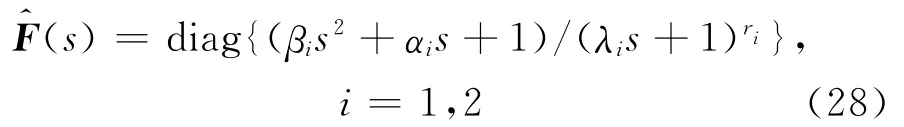
将其中的分子部分设计为可抵消缓慢极点或缓慢共轭极点的因式形式,λ1、λ2为可调待定参数.由上述可知,反馈回路滤波器为
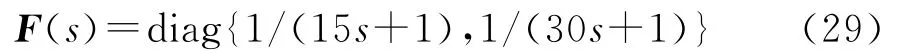
2.3 参数整定设计
理论上,所有优化算法再辅以合适的性能指标判定函数都可以应用于控制器参数的优化过程.前人对遗传(GA)算法、粒子群优化(PSO)算法和NLJ算法等进行了不少研究.性能指标普遍采用综合ISE或ITAE指标[15].笔者选取输出量和控制量的调节时间和超调量作为性能指标,同时兼顾对系统输出和控制器输出量的影响,并以潘立登[16]发展的NLJ算法作为寻优算法求取λ1和λ2在指定性能指标要求下的优化值.NLJ算法的具体过程在文献[16]中有详细论述,此处不再赘述.性能指标如下:
当r1=1,r2=0时
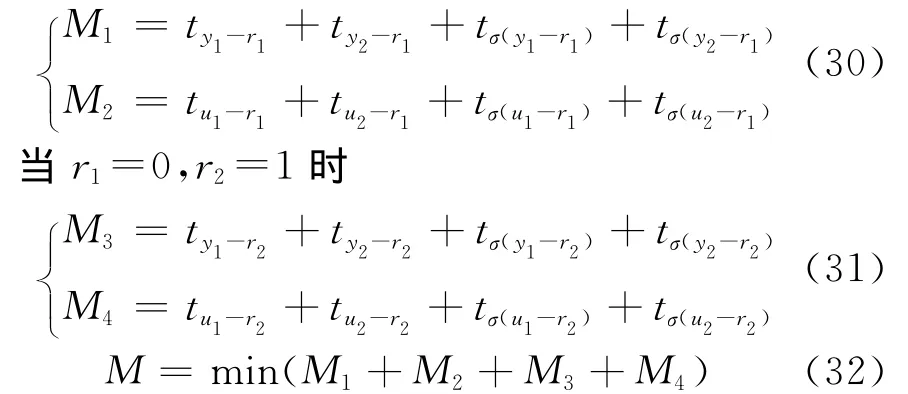
式中:ty1-r1和ty2-r1分别表示r1阶跃、r2不变时y1和y2的调节时间;ty1-r2和ty2-r2分别表示r2阶跃、r1不变时y1和y2的调节时间;tσ(u1-r1)和tσ(u2-r1)分别表示r1阶跃、r2不变时y1和y2的最大超调对应的时间;tσ(u1-r2)和tσ(u2-r2)分别表示r2阶跃、r1不变时y1和y2的最大超调对应的时间;其余符号的意义由此推知.
这样的设计可使所有被求量具有同样的量纲,且数量级相当,避免了“数量级淹没”的现象,优化可信度高.需要指出,在只能改变滤波器常数的情况下,调节时间和超调量是矛盾量.笔者设定系统输出量终值的误差容限为±2%,以此寻找调节时间和调节稳定性的最佳平衡.控制器输出量的误差容限为终值的±10%,在实际中控制器输出限值一般应超过稳态值1/3,以确保控制器和表计安全.
3 CFB锅炉燃烧系统内模解耦控制
3.1 求取(s)
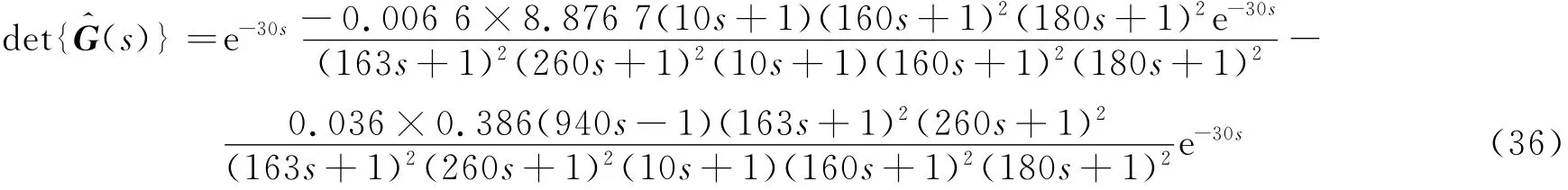
式(35)为高阶有理式,为方便后续控制器的设计,应对其进行有效的模型降阶处理.与整定滤波器常数类似,不少基于某些逼近条件的优化算法也被广泛应用于模型降阶中.文献[17]中提出采用性能指标J的次最优降阶方法.
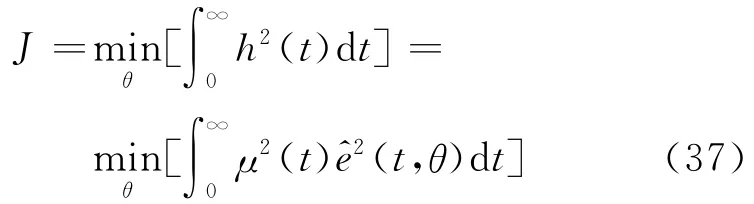
式中:h(t)为加权误差信号,h(t)=μ(t)e^(t);e^(t)为原始模型与降阶模型在相同输入信号下的误差,其中含有的迟延项采用pade逼近近似;μ(t)=tp为权重函数.易知,当p=0时,h(t)为ISE指标;当p=1时,h(t)为ISTE指标.
该降阶方法的特点是能够相对独立地选择降阶后模型分子、分母的阶次以及降阶后是否有迟延项,使用灵活,拓宽了其适用范围.方法中pade逼近的阶次亦可自由选择,而pade逼近可以任意精度逼近迟延项,借助计算机工具,降阶模型的精度得到保证.注意到式(35)的分母内部含有迟延项e-30s需要近似处理.尹先斌等[18]指出对于大迟延对象,一阶pade逼近可以获得满意效果,而全极点逼近则适用于所有时滞过程,可以获得较好的阶跃响应.2种逼近方法的形式如下:
一阶pade逼近
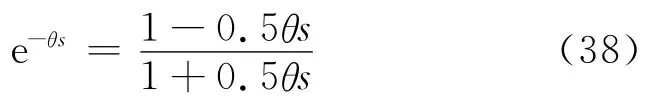
全极点逼近
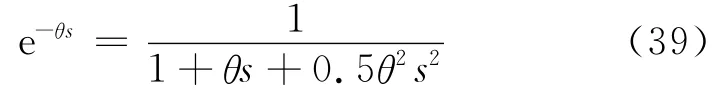
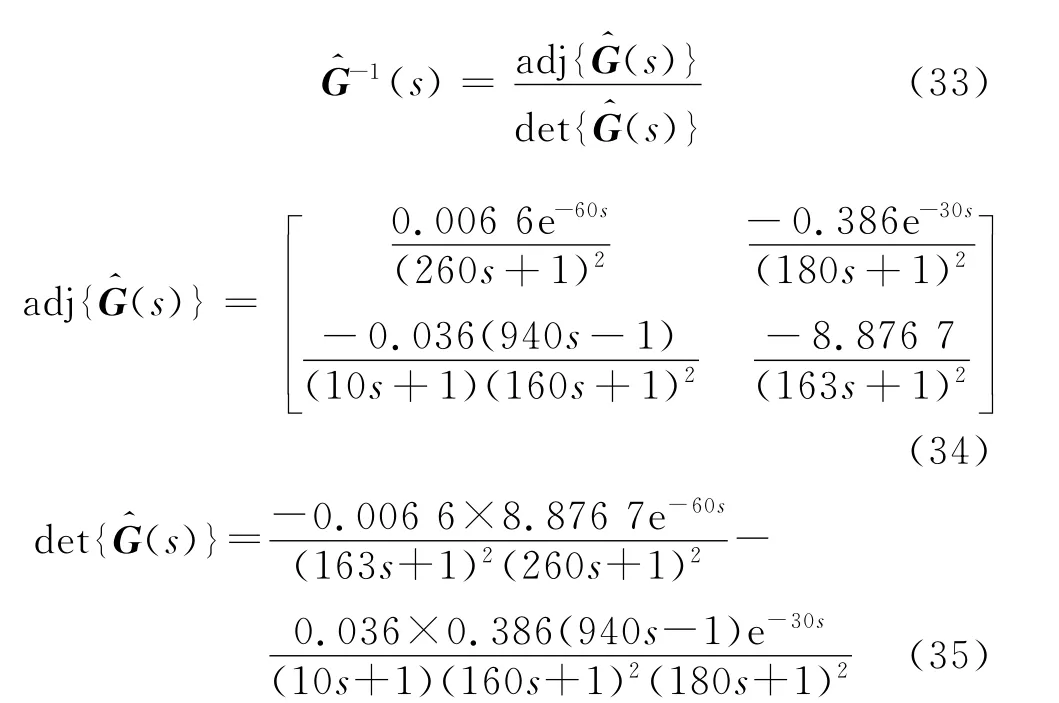
式(34)的理论迟延为30s.等式右边提取e-30s后通分的结果为
将原始对象与一阶pade逼近、全极点逼近效果进行比较发现,逼近效果差别细微.一阶pade逼近略好于全极点逼近,故本文选择前者.应指出,迟延项为公因式的一阶pade逼近将引入新的极点,而全极点逼近则不会引入新的极点.但对于分式内部的迟延项,一阶pade逼近与分子极点个数无直接关系.
应用次最优降阶方法对上述对象进行降阶,以不同阶次pade逼近对迟延项进行近似,比较后发现三阶pade逼近的效果较好.将对象降阶到分子、分母均为2阶且带迟延的低阶有理式
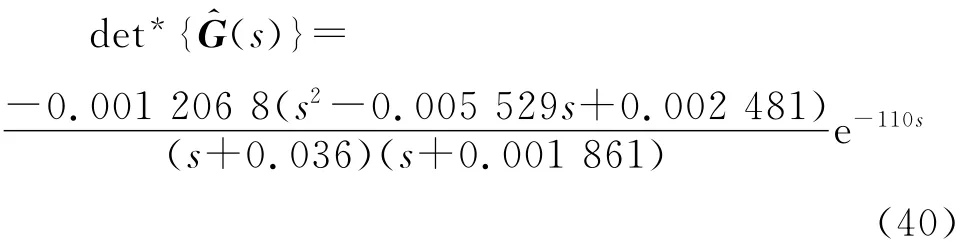
对比降阶前后对象的阶跃响应和Nyquist曲线,证实该方法的降阶效果较好.

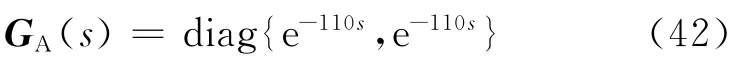
同时可知,矩阵各元素无零极点对消,故由等式
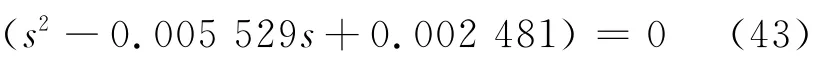
得到的根即为各元素唯一的公共不稳定极点.由此可知
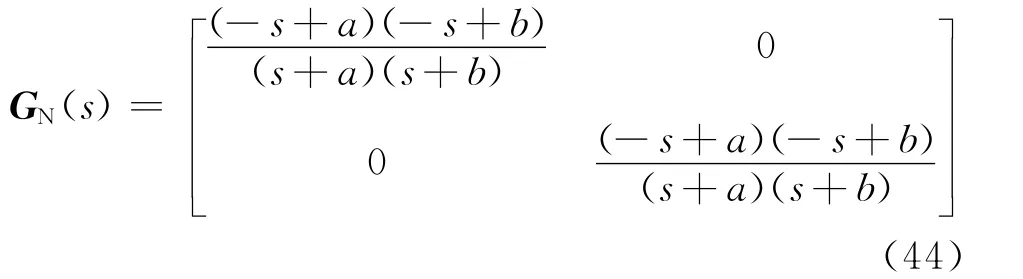
式中:a、b是式(38)的2个根,为共轭复根.
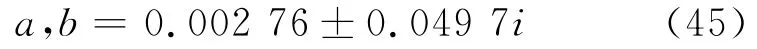
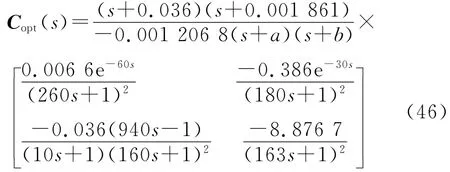
3.3 滤波器设计
考虑采用改进的滤波器设计方法来改善系统调节性能.注意到Copt(s)各元素中的缓慢极点(最靠近虚轴的点)均为因式(s+a)(s+b)的共轭复根,因此选取式(28)类型2作为滤波器的形式.为抵消该缓慢极点,可求得滤波器分子中β1=β2=403.063,α1=α2=2.229,分母阶次取2可满足要求,于是滤波器的形式变为
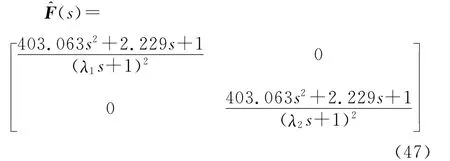
因此,得到控制器C(s)的各个元素为
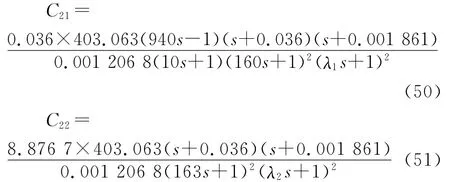
3.4 整定滤波器参数
笔者在大量的仿真实践中发现,对于本文对象,若采用ISE指标,指标持续单调递减,若采用ITAE指标,极小值点对应的λ1、λ2值在0.05附近.过小的时间常数将会降低系统的鲁棒性,同时超调量也偏大.
笔者采用基于NLJ算法寻优的综合了超调量和调节时间的性能指标,如2.3节所述.对于NLJ算法寻优的初始值,一般认为只要数量级相当即可[15,3],选取=80=80.将初始参数代入算法中迭代寻优50次,得到优化的时间常数值λ501=86.618,λ502=204.627.NLJ算法具有良好的收敛性,通常迭代20~30次即可找到最优值.
3.5 仿真分析
符号说明:r1为一次风量;r2为给煤量;u1为一次风量-床温通道控制器输出;u2为给煤量-主蒸汽压力通道控制器输出;y1为床温对象输出;y2为主蒸汽压力对象输出.
在标称情况下,且λ1=86.618,λ2=204.627,将改进滤波器的系统输出响应与式(24)形式的传统滤波器以及改进滤波器但固定时间常数(λ1=λ2=1.114)的系统输出响应进行比较,如图3所示.
以各变量响应保持在终值±2%作为调节进入稳态的指标,则可得表1和表2所示的性能指标.
同样条件下,比较控制量输出的响应(见图4).比较图4所示的输出阶跃响应可知,无论采用何种形式的滤波器,对象耦合效应均较好地解除,2个变量不相互影响.由表1和表2可知,对于控制通道的跟踪响应,将时间常数固定不变时,波形固定,调节时间和超调量等参数都较大,而且振荡也较其他方法剧烈.传统滤波器拥有最短的调节时间,但其超调量和振荡程度均大于不固定时间常数的改进滤波器.改进滤波器在优化参数后,拥有最平稳的控制曲线,但牺牲了调节时间.应指出,改进滤波器未有效缩短调节时间,原因在于对象的缓慢极点并非其闭环主导极点.各极点与虚轴的距离基本处在相同数量级,抵消缓慢极点未能有效改善响应速度.共轭负根极点比距虚轴相同距离的实数极点有更快的响应,抵消缓慢极点的同时引入了更多的极点个数,使得改进滤波器方法的调节时间变长.
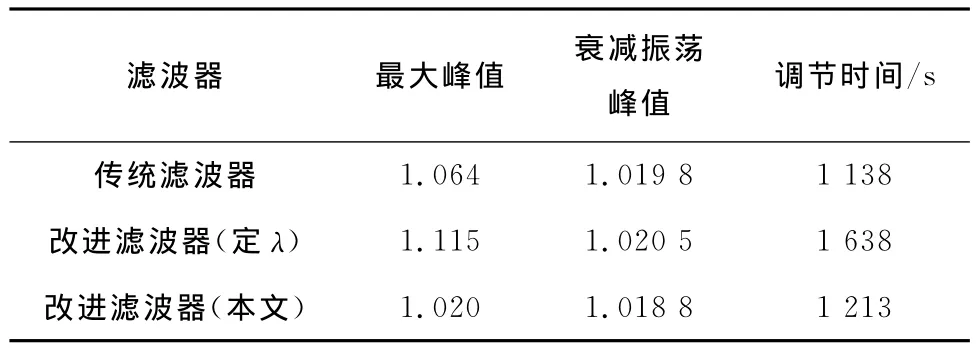
表1 r1=1、r2=0时y1的输出指标Tab.1 Output index of y1in the case of r1=1and r2=0
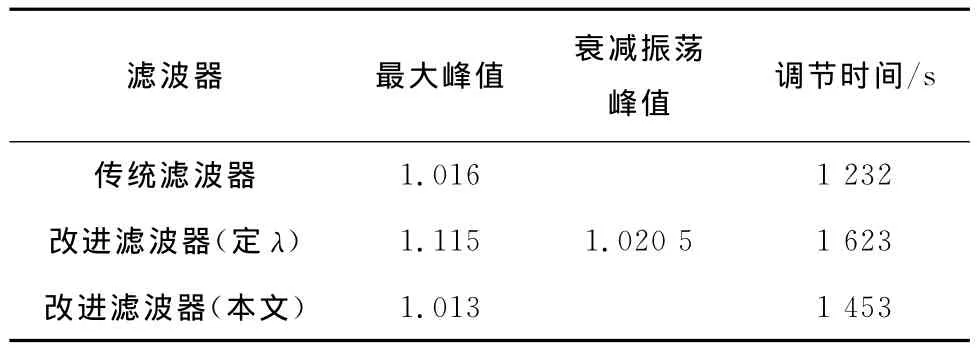
表2 r1=0、r2=1时y2的输出指标Tab.2 Output index of y2in the case of r1=0and r2=1
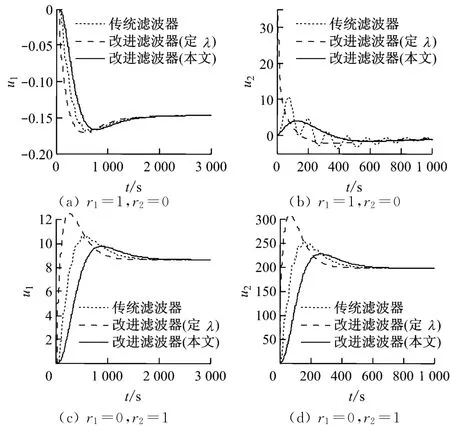
图4 控制量输出曲线的比较Fig.4 Comparison of control output curves among various filters
由控制量输出曲线可知,尽管不固定时间常数的改进滤波器依然表现出较长的调节时间,但平滑性很好,且控制器的动作幅度比另2种方法明显小很多.其中,固定时间常数的改进滤波器的动作量有时有突变,而传统滤波器则在调节过程中表现出明显的来回振荡,对控制器不利.综合上述,就控制的平稳性而言,不固定时间常数的改进滤波器有明显优势,且分析表明对于含主导极点的控制过程,抵消主导极点可以明显延长调节时间.
为验证控制系统的抗干扰能力,分别在过程对象前加入阶跃扰动,观察输出响应曲线.在2次仿真中,分别从床温和主蒸汽压力对象两者中的一个输入端加入设定值30%的扰动量(3 500s时),并观察另一输入端是否受影响,结果示于图5.
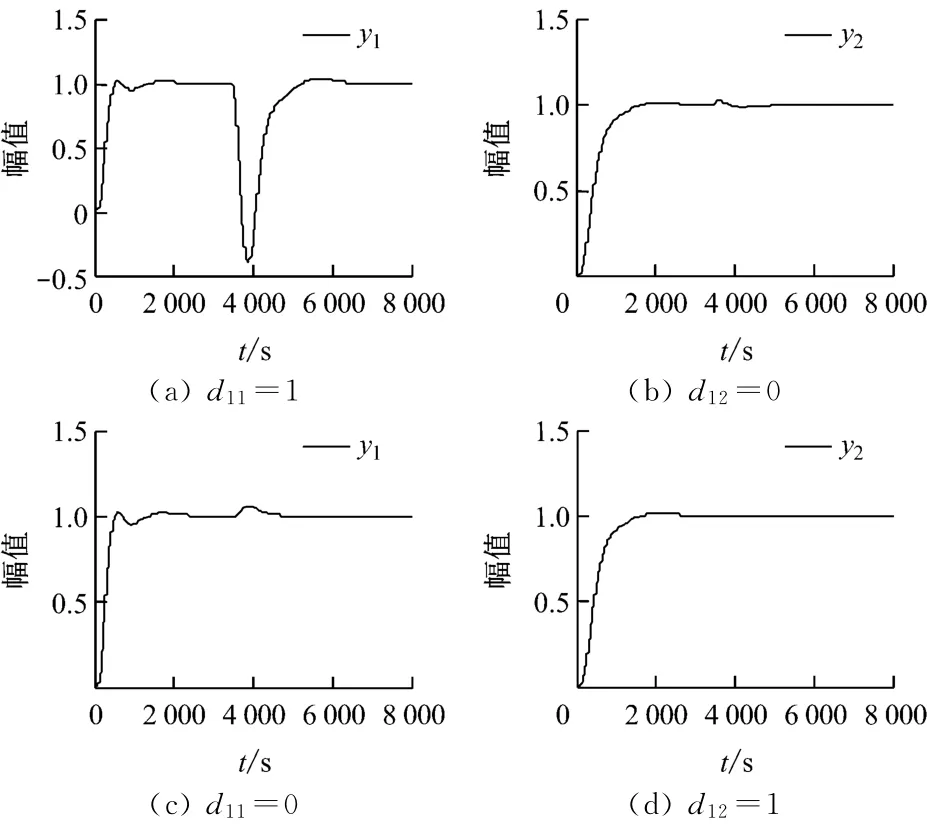
图5 输入扰动响应曲线Fig.5 System response under input disturbance
由图5可知,对于床温对象,在其输入端加入扰动时,响应出现明显的负调现象,这是由于一次风量阶跃升高确定的床温为负相关对象,干扰转化为风量信号叠加在一次风量上传递给对象,床温下降.负调幅度与该通道传递函数的增益成正比,同时也与扰动强弱有关.主蒸汽压力输入端的扰动对主蒸汽压力特性几乎没有影响.主蒸汽压力和床温在另一对象发生扰动时均有小幅波动,但均能迅速得到抑制.阶跃响应反映出系统能够有效地抑制输入扰动,但抑制效果仍需改善以达到更佳效果.
同理,在对象输出端加入阶跃扰动,观察输出的响应曲线.在2次仿真中,仅在不同对象的输出端加入设定值30%的扰动量(3 500s时),得到系统对输出扰动的响应曲线(见图6).
由图6可见,解耦系统对输出阶跃扰动具有良好的抑制作用,主蒸汽压力和床温几乎不受另一被控对象输出端扰动的影响.显然,滤波器时间常数的选择影响平复时间的长短,较小的时间常数有加快响应速度的作用.
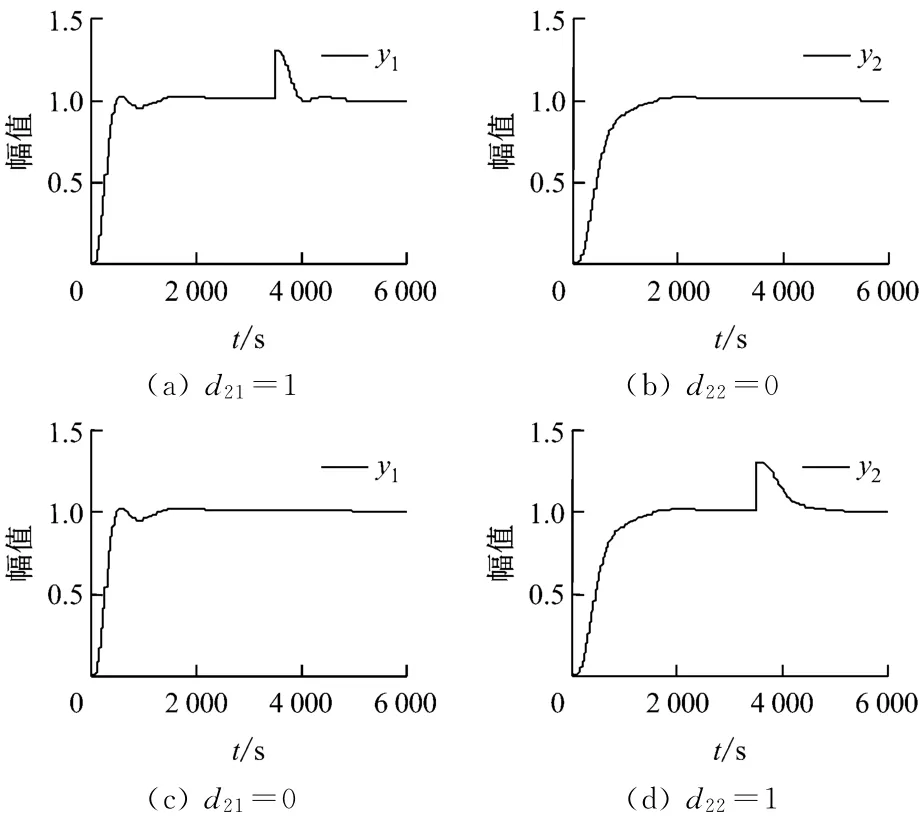
图6 输出扰动响应曲线Fig.6 System response under output disturbance
工业过程的复杂性决定了建模误差难以避免.为验证系统的鲁棒性,同时将过程对象的增益减小10%、迟延减小10%、惯性时间常数增大10%,得到图7所示模型失配时系统的响应曲线.
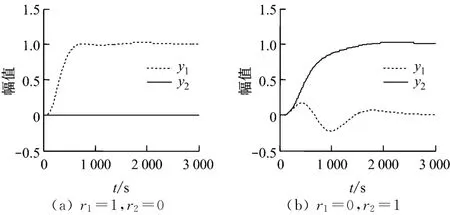
图7 模型失配时系统的响应曲线Fig.7 Response curves in the case of model mismatch
由图7可见,在存在一定建模误差的情况下,系统的解耦性能和响应效果比较令人满意.仿真发现,床温对迟延项和惯性时间常数较敏感,响应过程出现了较长时间的小幅波动,但能够得到有效控制.进一步研究可知,模型误差对床温和主蒸汽压力的影响基本一致.在标称系统中,主蒸汽压力和床温的耦合作用造成的波动大小数量级分别为10-10和10-7.在模型失配情况下,床温的波动达到10-1,而主蒸汽压力的波动也增大到10-4.这说明随着模型失配加剧,系统的波动幅度成指数级增大,控制性能逐渐恶化,内模控制模型对建模精度仍有一定要求.尽管内模控制具有强鲁棒性,系统最终仍能够稳定,但对于更大的模型误差,应考虑增强鲁棒性的措施.
鉴于控制器传递函数的阶数与控制器实际实现难度成正比,运用次最优降阶方法对原控制器传递函数矩阵的每个元素进行模型降阶.降阶后的低阶模型同时也能更方便地进行IMC-PID转化,以更好地应用到工业过程分散控制系统(DCS)中.将模型降阶到工业对象常见表达形式(一阶+迟延、二阶+迟延等),得到如下结果:

将该降阶控制器用于对象控制,效果见图8.由图8可知,降阶控制器对主蒸汽压力的控制效果比较理想,给煤量对床温的耦合作用能够基本消除,调节的平稳性也较好,但在调节初期存在明显负调.实际运行中,将CFB锅炉床温保持在最佳工作点附近即可,床温的小幅波动对燃烧和脱硫效率的影响是可以接受且不可避免的.但应看到,降阶前控制器对给煤量的控制并不存在负调,但降阶前后模型的时域吻合度好于频域吻合度,可考虑从频域角度(如RLS方法)进行模型降阶来设计低阶控制器.
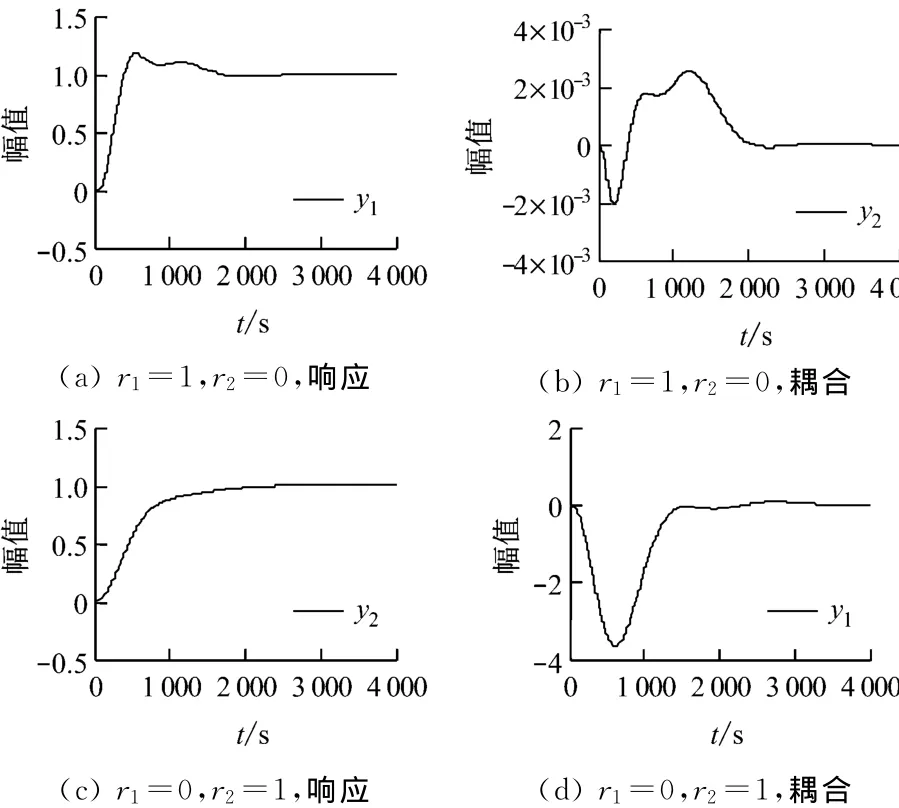
图8 降阶控制器的阶跃响应曲线Fig.8 Response curves of order-reduced controllers
4 结 论
(1)通过采用解析的多变量内模解耦控制方法,有效地对CFB锅炉中强耦合的床温和主蒸汽压力变量进行解耦.结果显示,本文改进方法对输入、输出扰动具有良好的抑制作用,对模型误差有较好的鲁棒性.
(2)解耦中采用了次最优降阶算法和迟延逼近方法,简化了复杂的运算和控制器的实现难度.采用NLJ优化算法和改进的滤波器形式来设计控制器,在仿真中取得较好效果.
[1]胡昌华,卢啸风.600MW超临界循环流化床锅炉设备与运行[M].北京:中国电力出版社,2012.
[2]王东风,王剑东,韩璞.一种多变量系统的内模解耦控制设计方法[J].控制工程,2003,10(5):463-465.WANG Dongfeng,WANG Jiandong,HAN Pu.New design of internal model decoupling control for multivariable system[J].Control Engineering of China,2003,10(5):463-465.
[3]JIN Qibing,QUAN Ling,QI Fei,et al.Internal model control for multivariable coupling system with time delays and optimization research[C]//Measuring Technology and Mechatronics Automation (ICMTMA),2010International Conference on IEEE.Changsha,China:IEEE Computer Society,2010:505-509.
[4]杨锡运,徐大平,张彬.再热汽温系统的内模解耦控制[J].动力工程,2004,24(4):529-532.YANG Xiyun,XU Daping,ZHANG Bin.Research on internal model control with decoupling in reheats temperature system[J].Power Engineering,2004,24(4):529-532.
[5]WANG Q G,ZHANG Y,CHIU M S.Decoupling internal model control for multivariable systems with multiple time delays[J].Chemical Engineering Science,2002,57(1):115-124.
[6]周平,柴天佑,陈通文.工业过程运行的解耦内模控制方法[J].自动化学报,2009,35(10):1362-1368.ZHOU Ping,CHAI Tianyou,CHEN Tongwen.Decoupling internal model control method for operation of industrial process[J].Acta Automatica Sinica,2009,35(10):1362-1368.
[7]CHEN J,HE Z F,QI X.A new control method for MIMO first order time delay non-square systems[J].Journal of Process Control,2011,21(4):538-546.
[8]靳其兵,袁琴.双输入双输出过程解耦内模控制[J].控制工程,2009,16(1):5-7.JIN Qibing,YUAN Qin.Decoupling internal model control for two-input two-output process[J].Control Engineering of China,2009,16(1):5-7.
[9]马素霞,杨献勇.循环流化床锅炉燃烧系统的动态特性研究[J].中国电机工程学报,2006,26(9):1-6.MA Suxia,YANG Xianyong.Study on dynamic behavior of the combustion system of a circulating fluidized bed bolier[J].Proceedings of the CSEE,2006,26(9):1-6.
[10]NORMEY-RICO J E,BORDONS C,CAMACHO E F.Improving the robustness of dead-time compensating PI controllers[J].Control Engineering Practice,1997,5(6):801-810.
[11]王伦,张卫东,刘永红.关于内外分解和谱分解问题的解析计算[J].上海交通大学学报,2007,41(6):889-893.WANG Lun,ZHANG Weidong,LIU Yonghong.The analytic computation of inner-outer and spectral factorization problems[J].Journal of Shanghai Jiaotong University,2007,41(6):889-893.
[12]ZHANG W,LIN C,OU L.Algebraic solution to H2control problems.II.the multivariable decoupling case[J].Industrial & Engineering Chemistry Research,2006,45(21):7163-7176.
[13]陈培颖,欧林林,孙敬,等.改进的内模控制方法及其在非方系统中的应用[J].控制与决策,2008,23(5):581-584.CHEN Peiying,OU Linlin,SUN Jing,et al.Modified internal model control and its application in nonsquare processes[J].Control and Design,2008,23(5):581-584.
[14]HORN I G,ARULANDU J R,GOMBAS C J,et al.Improved filter design in internal model control[J].Industrial & Engineering Chemistry Research,1996,35(10):3437-3441.
[15]RAO A S,CHIDAMBARAM M.Smith delay compensator for multivariable non-square systems with multiple time delays[J].Computers &Chemical Engineering,2006,30(8):1243-1255.
[16]潘立登.LJ最优化方法的改进[J].化工自动化及仪表,1985(1):10-15.PAN Lideng.An improvement in optimal tuning method with least performance index[J].Control and Instruments in Chemical Industry,1985(1):10-15.
[17]XUE D,ATHERTON D P.A suboptimal reduction algorithm for linear systems with a time delay[J].International Journal of Control,1994,60(2):181-196.
[18]尹先斌,周有训.基于Taylor和Pade能逼近的滞后系统IMC-PID研究[J].昆明理工大学学报:理工版,2006,31(2):76-79.YIN Xianbin,ZHOU Youxun.Taylor and Pade IMC-PID[J].Journal of Kunming University of Science and Technology:Science and Technology,2006,31(2):76-79.
