基于LS⁃SVR、BP⁃ANN和MLR模型的PM10浓度预测

冯晓秀，高志文，李风军，虎雪娇

1.宁夏大学数学计算机学院，宁夏 银川 750021

2.西安建筑科技大学环境与市政工程学院，陕西 西安 710055

基于LS⁃SVR、BP⁃ANN和MLR模型的PM10浓度预测

冯晓秀1，高志文1，李风军1，虎雪娇2

1.宁夏大学数学计算机学院，宁夏 银川 750021

2.西安建筑科技大学环境与市政工程学院，陕西 西安 710055

利用宁东能源化工基地PM10和气象监测数据，分别采用LS⁃SVR、BP⁃ANN和传统MLR模型预测PM10浓度变化。结果表明，较BP⁃ANN模型、MLR模型，LS⁃SVR模型能更好地刻画PM10浓度与各气象因素间的非线性相依关系，更准确地预测PM10浓度。

LS⁃SVR；BP⁃ANN；MLR；PM10；预测

为了解未来空气质量状况，合理安排工作与出行，环境空气质量预测和预报具有重要意义［1⁃7］。环境空气质量已有的预测方法［1⁃4］基本上需要构造影响因素与预测结果间的函数关系，并合理确定权重值。多元线性回归（MLR）模型［1⁃2］，可以对一些线性关系的浓度变化趋势进行很好的预测，而对PM10浓度与气象条件之间呈较强的非线性关系的情况就具有很大的局限性。人工神经网络（ANN），虽可以克服这一缺陷，能建立非常复杂的非线性映射，较好地反映PM10浓度与气象参数之间的非线性关系，但其拓扑结构需要结合经验试凑，很难小样本训练，在训练过程中易陷入局部极小值。

支持向量机（SVM）以小样本的统计学习理论（SLT）为基础，具有简洁的数学形式、直观的几何解释以及良好的泛化能力，有效避免了局部极值，克服了“维数灾难”，且人为设置的参数少，便于使用。最小二乘优化的支持向量回归机（LS⁃ SVR）已广泛应用于图像噪声处理、结构探伤等研究领域［9⁃11］，但在环境领域的应用鲜有报道。该文以宁东能源化工基地PM10浓度为例，分别利用基于LS⁃SVR、带误差反传算法（BP）的ANN及MLR进行PM10的预测和比较分析，以期为空气质量预测预报探索适合的模型算法。

1 方法原理

1.1 SVR原理

利用SVM解决非线性映射问题与分类问题类似，还是通过引入核函数将低维的非线性回归问题转化为高维的线性回归问题。其原理是根据给定的训练集：

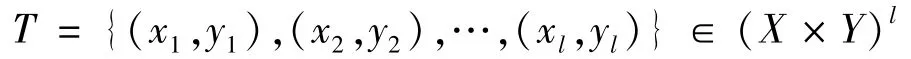
式中：xi∈X＝Rn是输入，yi∈Y＝R是输出，寻找一个实值函数f（x），并用来推断任一输入x所对应的输出y［9］。分类问题所求的超平面，实际上就是回归问题的解。这样的SVM称为支持向量回归机（SVR）。

SVM的拓扑的结构与一个3层前馈神经网络的结构类似。其中隐层节点对应于输入样本与一个支持向量的内积核函数，而输出节点对应于隐层输出的线性组合。图1给出了SVM的拓扑结构示意图。

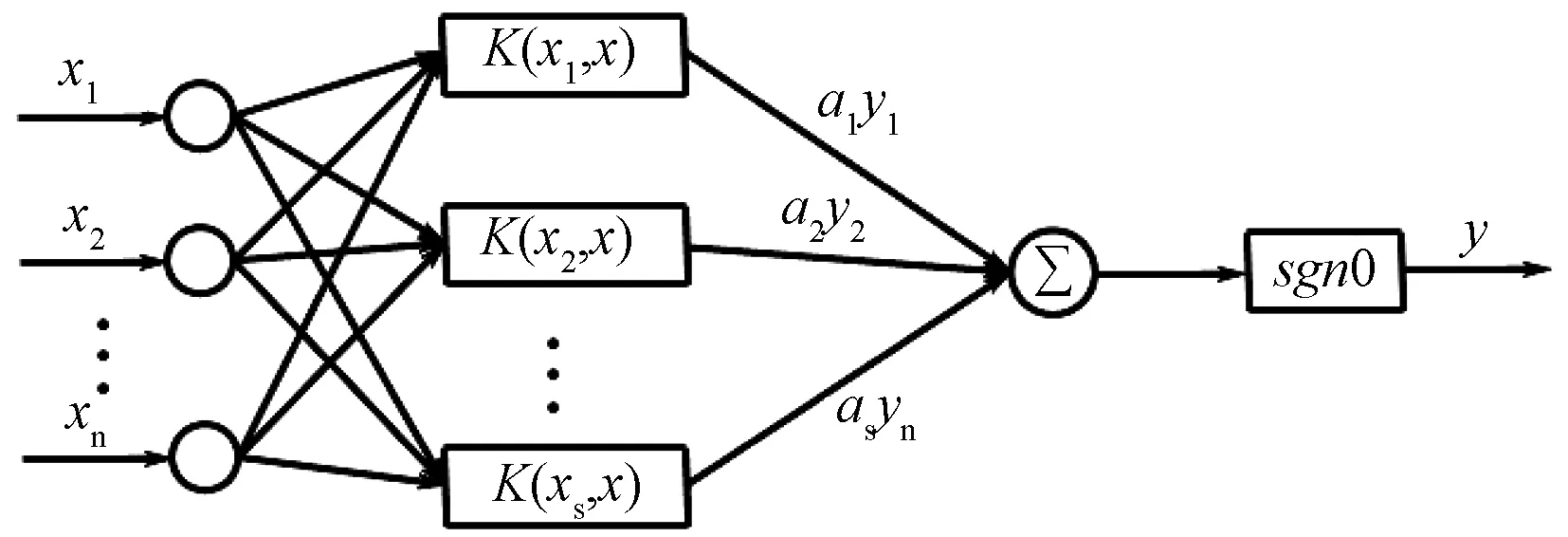
图1 SVM拓扑结构

回归问题的求解可利用最小二乘法，用以加快求解速度，能更好更快地进行预报，这样的模型称为LS⁃SVR［9］。

1.2 数据源

利用宁东环境监测站4个环境空气点位的PM10浓度小时值，监测时段分别为冬季（2012年1月1—31日）、春季（2012年3月15日至4月15日）、夏季（2012年6月10日至7月15日）、秋季（2012年8月20日至9月22日），每天监测24 h。同时收集气象数据包括风速、温度、相对湿度、日照、降雨量等。所有的模型选取其中的1 000组原始数据用于学习训练，另外选取800组数据用于验证。

2 模型建立

2.1 输入信号选取

大气颗粒物PM10的浓度受多种气象条件的影响，通过参考文献［3⁃5］以及实地调研，决定选取的输入参数有初始浓度风速（v，m／s）、温度（T，℃）、相对湿度（H，%）、压力（p，kPa）、降雨量（R，mm）、日照（S，h）。

2.2 LS⁃SVR预测模型

采用Matlab7.8建立LS⁃SVR模型，LS⁃SVR模型中的核函数一般需要构造，且必须满足Mercer定理，考虑到适用性以及便捷性，选取径向基函数中的Gauss函数：

式中：xi为训练数据点，σ为函数的宽度参数，控制了函数的径向作用范围，这一宽度越小，就越具有选择性［1］。

建立模型时要对搜集到的输入数据进行归一化，常用的归一化函数有指数函数法、最大最小值法［3］等，研究采用最大最小值法进行归一化处理。归一化处理后，使用交叉验证的方法选择参数（σ，c）＝（10，5）作为模型参数对模型进行训练和验证，最后通过计算预测结果的相对误差来评价模型精度。

2.3 BP⁃ANN预测模型

利用Matlab7.8中的ANN工具箱建立BP⁃ANN预测模型。BP⁃ANN预测模型中输入信号与LS⁃SVR模型相同，即输入层有7个节点；输出层为PM10浓度，所以只有一个节点；隐层节点的选取利用经验公式

式中：n为输入层神经元数，m为输出层神经元数［11］。传递函数选取最常用的S型函数：

2.4 MLR预测模型

利用Matlab 7.8统计工具箱建立MLR模型，来与LS⁃SVR及BP⁃ANN建立的模型进行比较。利用的多元线性回归模型如下：

式中：xi为第i个输入变量的值；y为实测PM10浓度；常数项b0和回归系数bi通过最小二乘法获得；εi为回归误差，回归求解的过程事实上就是使平均误差ε最小的过程。

3 结果及分析

3.1 模型精度比较

表1给出了3种模型的预测统计结果，在方差相同的情况下，LS⁃SVR模型的预测相对误差最小，命中率最高。

表1 预测统计结果

图2给出了3种模型预测值与实测值相关性，图2（a）、图2（b）、图2（c）分别为MLR、BP⁃ANN、LS⁃SVR预测模型的结果。经显著性水平α＝0.05相关系数显著性检验后，MLR预测模型的相关系数（r）仅为0.50，BP⁃ANN预测模型R为0.83，LS⁃SVR预测模型（r）最高为0.97，且斜率也更接近于1，说明该模型预测值与实测值具有显著相关性。

图3利用全年实测值以及各模型预测值的24 h各时刻均值，展示了各模型在时间序列下的拟合程度，其误差比较见表2。可见，LS⁃SVR预测模型曲线更切合实测值曲线，能更好地预测PM10浓度变化；BP⁃ANN模型整体预测效果也较为理想，但是傍晚时段的预测结果偏差较大；MLR预测模型与实际结果的拟合程度相差太多，该模型仅仅能预测PM10浓度的平均变化趋势。

图3 预测值与实际测量值全年24 h变化

表2 不同预测模型的误差比较

3.2 影响因素分析

因为LS⁃SVR、BP⁃ANN模型均为非线性映射，所以无法直接输出每个影响参数的权值大小，但由MLR预测模型可粗略看出各参数影响。利用Matlab7.8统计工具箱建立的MLR预测模型如下：

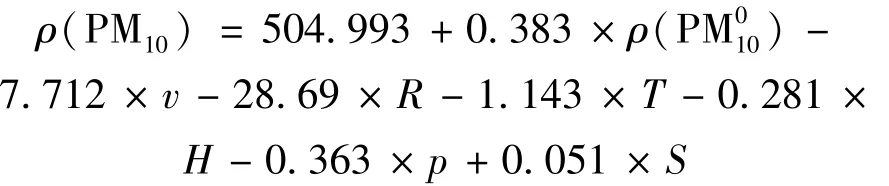
式中：ρ（PM10）为预测质量浓度，ρ（PM010）为初始质量浓度，可见，初始浓度、降雨量、风速、温度、压力等是影响PM10浓度的重要因素。

利用LS⁃SVR模型进行预测，给出了不同降雨量下大气颗粒物PM10浓度模拟值的24 h变化，见图4。

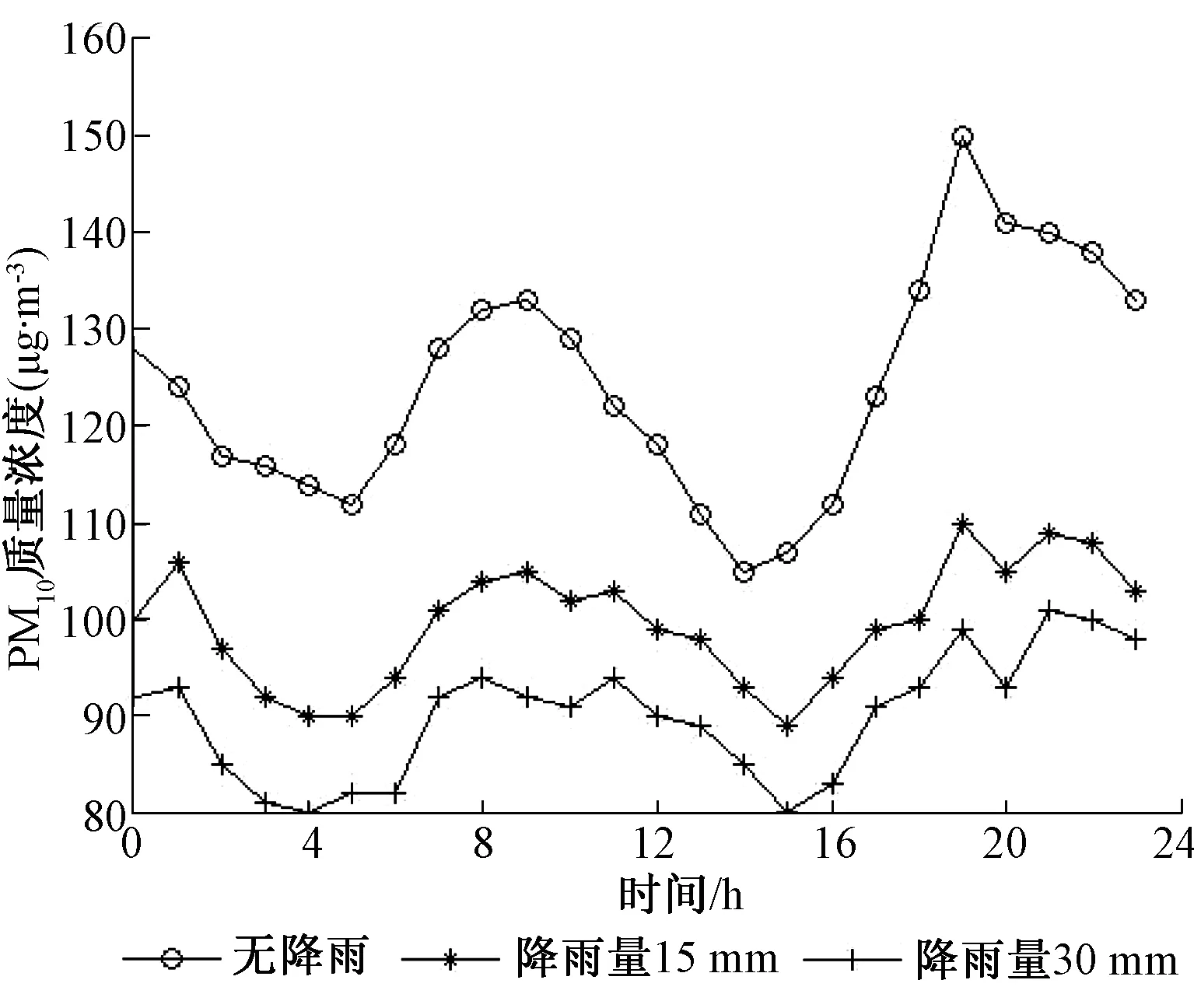
图4 不同降雨量下PM10浓度模拟值的24 h变化

降雨量增加可以明显降低PM10浓度，平均减少量为17.28%。但是如果继续增加降雨量，PM10浓度减少量也将会下降，不会呈现等差比例的下降。说明可以通过增加降水或者类降水（洒水车）的方法来降低PM10浓度。PM10浓度影响因素有很多，各因素之间是一种非线性关系，所以当降水的影响因素饱和之后，它的影响将逐渐减少，而其他因素将会占主导地位，这也是持续增加降水量PM10浓度减少量变小的原因。

4 结论

较BP⁃ANN模型、传统的MLR模型，LS⁃SVR预测模型可以很好预测大气颗粒物PM10浓度，可以作为预测PM10浓度的首选算法。控制各污染源（如火电、煤矿、煤化工等）的排放，增加降水或者类降水可有效降低PM10浓度。

［1］石灵芝.城市大气颗粒物PM10源解析与浓度预测及气象因素影响研究［D］.长沙：中南大学，2011.

［2］石灵芝，邓启红，路婵，等.基于BP人工神经网络的大气颗粒物PM10质量浓度预测［J］.中南大学学报：自然科学版，2012.5，43（5）：1 969⁃1 974.

［3］周国亮，刘希玉，武鲁英.BP神经网络模型在空气质量级别评价中的应用［J］.计算机工程与设计，2009，30（2）：392⁃394.

［4］王灿星，侯树强.杭州市区大气中PM10等污染物的预测研究［J］.仪器仪表学报，2004，25（4）：780⁃781.

［5］龚识懿，冯加良.上海地区大气相对湿度与PM10浓度和大气能见度的相关性分析［J］.环境科学研究，2012，25（6）：628⁃632.

［6］殷永文，程金平，段玉森，等.上海市霾期间PM2.5、PM10污染与呼吸科、儿童呼吸科门诊人数的相关分析［J］.环境科学，2011，32（7）：1 894⁃1 898.

［7］包贞，冯银厂，焦荔，等.杭州市大气PM2.5和PM10污染特征及来源解析［J］.中国环境监测，2010，26（2）：44⁃48.

［8］Tecer L H.Prediction of SO2and PM10concentrations in a coastal mining area using an artificial neural network［J］.Polish Journal of Environmental Studies，2007，16（4）：633⁃638.

［9］渐令.支持向量机在高炉炉温预报中的应用［D］.杭州：浙江大学，2006.

［10］孙红星，赵楠楠，徐心和.基于SVM的模糊推理在图像降噪中的建模与仿真［J］.系统仿真学报，2006，18（26）：3 276⁃3 279.

［11］韩立群.人工神经网络教程［M］.北京：北京邮电大学出版社，2007.

［12］Mouhammd A，Alaa F S，Hossam F.Prediction of PM10and TSP airpollution parametersusing artificial network autoregressive，external input model：a case syudy in Salt，Jordan［J］.Middle⁃East Journal of Scientific Research，2013，14（7）：999⁃1 009.

［13］Ana R，Frank R，Pedro G L.Air quality prediction using neural networks with stochastic variables［J］. Atmospheric Environment，2013（79）：822⁃830.

Prediction of PM10Concentrations Based on LS⁃SVR，BP⁃ANN and MLR Models

FENG Xiao⁃xiu1，GAO Zhi⁃wen1，LI Feng⁃jun1，HU Xue⁃jiao2
1.School of Mathematics and Computer Science，Ningxia University，Yinchuan 750021，China
2.College of Environmental and Municipal Engineering，Xi’an University of Architecture and Technology，Xi’an 710055，China

Using ambient PM10concentrations and meteorological data of Ningdong Energy and Chemistry Industry Base，predicted PM10concentrations variation based on LS⁃SVR，BP⁃ANN and traditional MLR models，respectively.It was shown that the LS⁃SVR model could better depict the nonlinear dependency relationship between PM10concentrations and meteorological factors，more accurately predict PM10concentrations，comparing to BP⁃ANN and MLR.

LS⁃SVR；BP⁃ANN；MLR；PM10；prediction

X831.03

A

1002⁃6002（2014）06⁃0138⁃04

2013⁃11⁃20；

2014⁃04⁃14

国家自然科学基金资助项目（61063020，11261042）

冯晓秀（1990⁃），女，宁夏盐池人，在读硕士研究生.

李风军