城市PM2.5扩散网络模型的研究
2014-07-10张晓勇王仲君
张晓勇,王仲君
1.武汉理工大学理学院数学系,湖北武汉430070
2.武汉理工大学理学院统计系,湖北武汉430070
所有Wij(t)构成的集合,记为W1。容量网络的邻接矩阵为
城市PM2.5扩散网络模型的研究
张晓勇1,王仲君2
1.武汉理工大学理学院数学系,湖北武汉430070
2.武汉理工大学理学院统计系,湖北武汉430070
以复杂网络理论为基础,运用最短增广链算法构建城市PM2.5扩散的容量网络模型。通过分析城市环境中水平距离、海拔、风力等因素的作用,对PM2.5区域性扩散的物理过程进行一次有益的探索。西安市近期空气监测数据的实证分析显示,预测值与监测值基本吻合。同时,模型输出揭示了西安市PM2.5的扩散途径。
复杂网络理论;最短增广链算法;PM2.5扩散
PM2.5扩散研究已成为学术界的热点问题,现已提出不少模型,如高斯扩散模型、微分方程模型等[1],但取得的实际效果参差不齐。而在复杂网络上的物理传输过程研究,如流行病的传播、谣言的扩散、节点间的同步和协同行为等均取得阶段性成果[2]。PM2.5监测刚起步,导致基于复杂网络理论的PM2.5扩散模型研究还很少。
PM2.5作为一种悬浮于大气中的细微颗粒物[3],它的扩散机理符合复杂网络的动力学机制[4]。运用复杂网络理论以及复杂系统动力学的有关知识,依据地理因素把城市划分成若干区域,建立以各个区域为节点的容量网络模型。根据已证实的显著影响PM2.5区域性扩散的各种因素,如风力、海拔、水平距离等[5]来确定容量网络的弧权,进而确立基于最短增广链算法的PM2.5在容量网络上的扩散动力学机制,以期对城市各个区域的PM2.5浓度做出准确实时预测。
1 建立容量网络模型
1.1 构建网络
在城市环境中,PM2.5的扩散是一个十分复杂的过程。扩散结果取决于各种因素,如水平距离、海拔、风力、空气湿度等的共同作用。为避免模型过于复杂,做如下假设:
1)把城市中按地理位置划分的各个区域定义为节点,任意2个节点双向连接,构建一个n阶有向网络N(V,A,W)。其中,V是节点集,A是弧集,W是弧的最大负载量集。任意节点i的质量浓度用Ci(μg/m3)表示。
2)对任意弧aijA,若节点i和j的实际水平距离超过35 km,将aij、aji断开。
3)对任意弧aij∈A,若节点i处海拔比j处低,且超过50 m,将aij断开。
4)对任意弧aijA,设aij的最大负载量为wij,处理后的网络记为N1(V1,A1,W1)。
1.2 确定弧权
2个区域的距离越远,海拔高度差越大,浓度差越小,PM2.5的扩散难度越大[6]。此外,顺风向有助于PM2.5的扩散,逆风向阻碍PM2.5的扩散[7]。设任意2个节点i和j(i,j∈V1,且i≠j)的高度差为ΔHij(m),水平距离为ΔSij(km),PM2.5浓度差为ΔCij(μg/m3)。根据气体扩散理论和上述假设,t时刻wij为
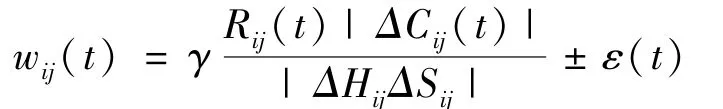
式中:γ是校正系数,取值范围为(0,1);ε(t)是最大负载量wij(t)在一个周期内波动的最大值。设由节点i到节点j的实际方向为节点i处的风力为(m/s),θij(t)是和的夹角。依据大气流动力学理论,风力系数Rij为
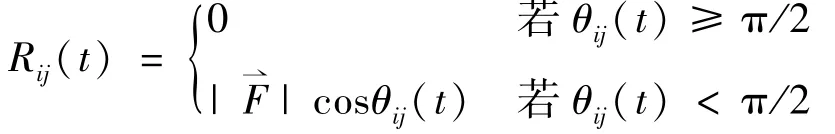
所有Wij(t)构成的集合,记为W1。容量网络的邻接矩阵为

1.3 模型的动力学机制
1.3.1 最短增广链算法的原理
在一个带有源点s和汇点t的容量网络上搜索得到的一个流量最大的可行流,称之为最大流。求最大流的常见方法是最短增广链算法,其基本原理如下:若P是N1中连接源点s和汇点t的一条链,定义链的方向是从s到t,则将P上的弧分成2类:一类为弧和链的方向一致,称为向前弧,向前弧的全体记为P+;另一类为弧和链的方向相反,称为向后弧,向后弧的全体记为P-。若f是N1上的一个可行流,P满足下列2个条件称为可增广链:
1)∀(Vi,Vj)∈ P +,且 fij< wij,即不饱和弧。
2)∀(Vi,Vj)∈P-,且fij>0,即非空弧。
若N1中有一个f的增广链P,则f不是最大流,需要增流[8]。直到N1中不存在关于f的增广链,此时的f就是网络中的最大流。
算法的主要步骤如下:
1)在N1上任取一个可行流f0作为初始可行流,令k=1。
2)用广度优先搜索(BFS)方法[9]搜索fk的增广链,若无则转入4)。
3)对fk进行增广[9],令k=k+1,转入2)。4)fk即为最大流。
1.3.2 模型的演化规律
对于容量复杂网络模型N1(V1,A1,W1),设T=24 h为1个周期。以PM2.5浓度突然激增的节点为源点(S),依次以其余各个节点为汇点。基于上述算法,求由源点至汇点的最大流量fsi,并依次叠加到浓度较低的对应节点上。在一个周期内,进行一次更新,可得各个区域PM2.5浓度值随时间演变的规律,即Ci(t+T)与Ci(t)的关系为

从t时刻至t+T,容量网络的最大负载量集W1及邻接矩阵M(N1)也随之变化。
2 数据来源
以西安市13个监测点记录的2013年1月1日至4月26日的PM2.5监测数据(源于西安市环境保护局网站:http://www.xaepb.gov.cn)为依据进行实证分析。13个监测点的距离和海拔数据来源于Google earth软件数据库,如表1所示。
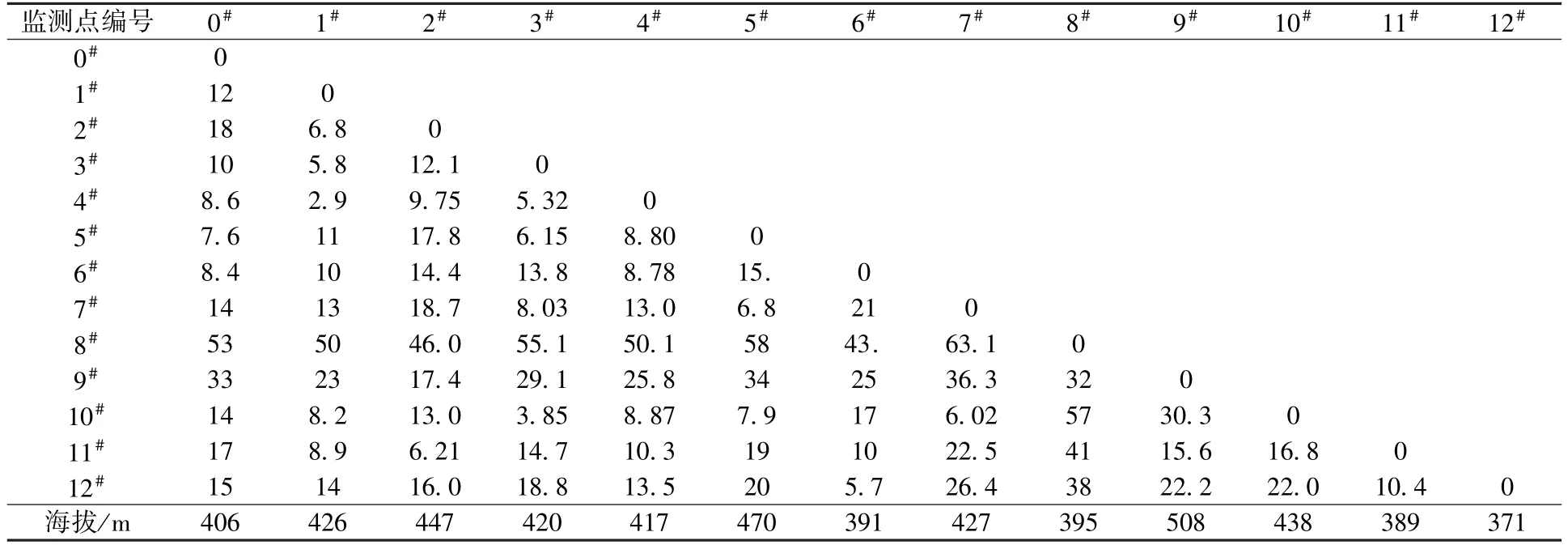
表1 各个监测点海拔以及它们之间的距离 km
依照上述方法构建容量网络N0(V,A,W)。通过分析西安市各监测点2013年1月1日至4月26日的PM2.5浓度数据,发现处于工业区的高压开关厂(0#监测点)共有114 d的记录,其中,中重度及以上污染程度的天数为91 d,占比约为80%,且此区域的其他各项空气污染指数都比其余区域高。因此,该区域是一个长期遭受空气污染的区域,可将其作为容量网络中的源点,依次以其余12个监测点为汇点。经多次模拟分析发现,校正系数γ取0.1时效果较好。
3 实证结果的讨论与分析
3.1 最大流量
2013年1月13日0#监测点的PM2.5质量浓度为399 μg/m3,而次日迅速激增至500 μg/m3。基于最短增广链算法对各区域污染程度进行模拟仿真得到1个周期内0#监测点到其余12个监测点的最大流量,如表2所示。

表2 高压开关厂在1个周期内到其余12个监测点的最大流量 μg/m3
3.2 预测值与监测值的比较
依据模拟结果和1月13日各个监测点的监测值,对14日各个监测区域的PM2.5浓度进行预测,预测值与监测值以及它们之间的偏差量如图1和表3所示。
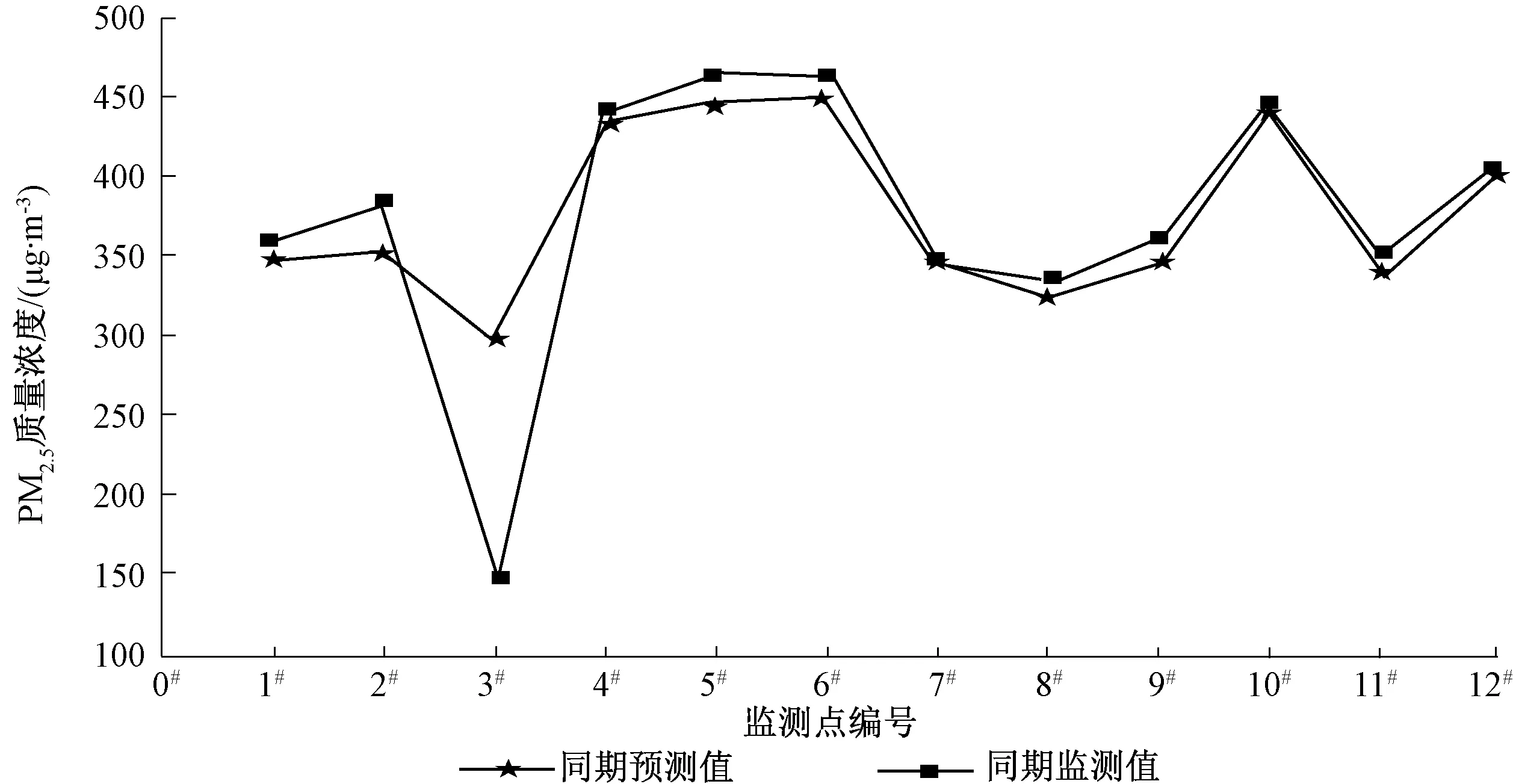
图1 2013年1月14日各监测点监测值与预测值对比

表3 12个监测点的预测值及偏差量
从图1、表3可看出,预测值较为贴近监测值,除了3#监测点处的预测偏差较大外,其余点的预测偏差百分率不超过8%,大部分在5%以内。
分析3#监测点出现较大偏差的原因认为:①小寨位于西安市南郊,是西安市的科教文化旅游胜地之一。此区域的绿化率较高,空气湿度较大。②当日此区域空气中的其他污染成分(NO2、O3、SO2)浓度均偏低,而 PM2.5的化学成因与 NO2、O3、SO2等有密切关系[3]。
表3中的监测值一般大于预测值,表明每个区域的PM2.5浓度除了受扩散的影响外,自身区域范围内也会产生PM2.5,如汽车尾气、施工扬尘等。个别出现监测值小于预测值情况,应属模型误差范围。在容量网络模型中,弧权的确定十分关键,影响弧的因素又很多,难以考虑所有可能的因素,这是产生预测误差的主要原因。由此可见,充分掌握各个监测区域的地理特征、天气状况等自然条件对于模型的改进十分必要。
3.3 扩散路径
系统分析12次的模拟结果,统计出经过弧的流量总和最大的15条弧,得到以高压开关厂为点源的PM2.5扩散途径,如图2所示。
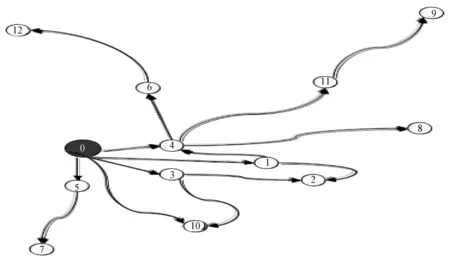
图2 以高压开关厂为点源的PM2.5扩散路径示意图(13个编号所代表的区域与地理位置一致)
总体上距污染源越近的区域受到的影响越大,但在个别区域出现了差异。如5#监测点,虽然距污染源较近,扩散流量反而没有距污染源更远的1#监测点的扩散流量大。可见,扩散路径并非完全由点源距离决定,还与海拔高度差、风力等因素有密切关系。
尽管PM2.5在城市大气中的扩散过程十分复杂,但是选用复杂网络理论进行PM2.5的扩散模拟是一条可行的途径。基于复杂网络理论的PM2.5扩散模型研究刚起步,有待进一步深入,以期实现对城市各区域PM2.5污染程度更为准确的实时预测。
[1]迟妍妍,张惠远.大气污染物扩散模式的应用研究综述[J].环境污染与防治,2007,29(5):376⁃381.
[2]霍良安,黄培清.突发事件中的谣言扩散问题研究:以日本大地震为例[J].情报杂志,2011,20(10):77⁃ 81.
[3]邵龙义.城市大气可吸入颗粒物物理化学特征及生物活性研究[M].北京:气象出版社,2006:58⁃62.
[4]何大韧,刘宗华,汪秉宏.复杂系统与复杂网络[M].北京:高等教育出版社,2009:148⁃220.
[5]云慧,何凌燕,黄晓锋,等.深圳市PM2.5化学组成与时空分布特征[J].环境科学,2013,34(4):1 245⁃1 251.
[6]穆珍珍,赵景波,徐娜,等.西安市雁塔区冬季可吸入颗粒物时空变化研究[J].环境科学学报,2011,31(7):1 509⁃1 516.
[7]徐永海,赵雪艳,姬亚芹.东营春季PM10中有机碳和元素碳的污染特征及来源[J].中国环境监测,2013,29(1):8⁃12.
[8]谢政.网络算法与复杂性[M].长沙:国防科技出版社,2003:118⁃123.
[9]李明哲,金俊,石瑞银.图论及其算法[M].北京:机械工业出版社,2010:45⁃47.
The Study of Diffusion Networks Model of about PM2.5in Urban Areas
ZHANG Xiao⁃yong1,WANG Zhong⁃jun2
1.The Math Department of Science School of Wuhan University of Technology,Wuhan 430070,China
2.The Statistics Department of Science School of Wuhan University of Technology,Wuhan 430070,China
Build the capacity network diffusion model of PM2.5in urban areas with the algorithm of the shortest augmenting chain based on the theory of complex network.By analyzing the influence of various factors including horizontal distance,altitude and wind power,explore the physical transfer process of PM2.5in urban areas.Following instance analysis with Xi’an air quality data showed that predicting values and actual measured values were generally consistent.Meanwhile the output of model reveals the diffusion pathways of PM2.5in Xi’an.
the theory of complex network;the algorithm of the shortest augmenting chain;the diffusion of PM2.5
X831.03
A
1002⁃6002(2014)06⁃0129⁃04
2013⁃10⁃09;
2014⁃02⁃23
国家自然科学基金资助项目(71140015);中央高校基本科研业务费专项资金(2013⁃Ia⁃040)
张晓勇(1988⁃),男,河南民权人,硕士,工程师.
