改进的小波阈值函数在水电机组振动信号降噪中的应用

高曙光

（眉县万家塬水电站，陕西宝鸡722300）

改进的小波阈值函数在水电机组振动信号降噪中的应用

高曙光

（眉县万家塬水电站，陕西宝鸡722300）

小波阈值降噪是水电机组振动信号除噪常用的方法，传统降噪算法是软、硬阈值函数，对于硬阈值函数处理过的信号，其重构后的信号在阈值处是间断的，易产生附加振荡；而经软阈值函数降噪后的信号虽然连续性好，但与原始信号之间存在着恒定的偏差，影响重构精度。因此在传统软、硬阈值函数的基础上提出了一种改进阈值函数的小波降噪算法，通过Matlab仿真和电厂采集数据的验证表明，该方法克服了软、硬阈值函数算法的缺点，去噪效果明显。通过比较不同降噪方法对振动信号特征分量的保持程度，说明该方法在各分量保持均优于传统的阈值方法，是一种有效的降噪方法。

水电机组；振动信号；小波去噪；阈值函数

在水电厂机组状态监测的主要参数有压力、温度、振动、摆度、电流和电压等，其中对振动和摆度信号的监测最为普遍，因为水电机组约有80%的故障或事故都在振动信号中有所反映［1］。因此对机组的振动信号进行监测，及时发现和排除故障，对机组安全稳定运行至关重要。由于水电机组本身和环境因素，监测到的信号中必有噪声，为了保证能准确地诊断出机组故障，就必须对监测到的信号进行降噪处理。

传统的信号降噪方法主要有傅立叶变换，短时傅立叶变换、Wigner－Ville、小波变换等。傅立叶变换将信号的能量平均分布在整个时间段内，对于振动非平稳故障信号，不能反映故障信号局部的信息；短时傅立叶变换具有一定的局部分析能力，但是其窗函数若选定了大小就不会再发生变化，故短时傅立叶变换不能自适应时频位置的变化；Wigner－Ville分布虽然能同时在时域、频域中表达信号，且其分辨率也不错，但针对多分量信号会产生交叉干扰项［2］。小波变换将信号分解在时间—尺度的相平面上，其伸缩因子和平移因子构成的窗函数能够自适应信号的变化，因此小波变换非常适合非平稳信号的降噪，在信号去噪方面表现出明显的优势。1995年，Donoho D L在小波变换的基础上提出了小波阈值去噪算法［3］，但传统的软、硬阈值函数存在着一定的缺点［4］，本文在其基础上提出了一种改进的阈值函数。通过实验表明，改进的阈值函数克服了传统阈值函数的缺点，且去噪效果明显，通过比较不同降噪方法对振动信号特征分量的保留程度，说明该降噪方法优于传统方法，应用价值较高。

1 传统的阈值函数分析

传统的硬、软阈值函数的去噪算法简单明了，选择合适的小波函数将含噪信号分解后，若分解得到的高频空间某点的小波系数的绝对值不大于阈值，则直接将其置零，否则该点值不变或变为该点值与阈值之差［7］。

硬阈值函数为：

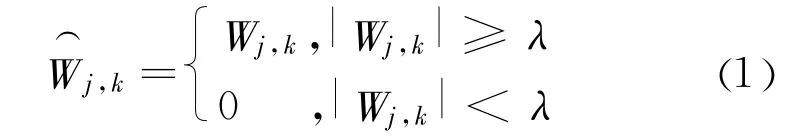
软阈值函数为：

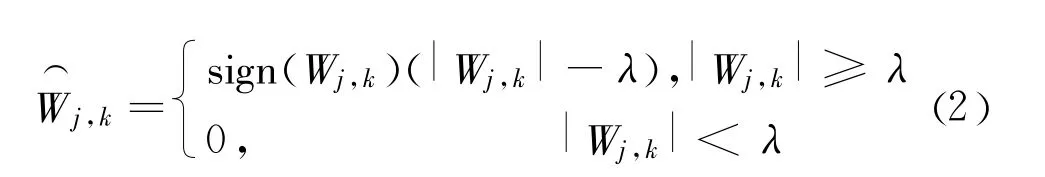
其中λ为阈值，即

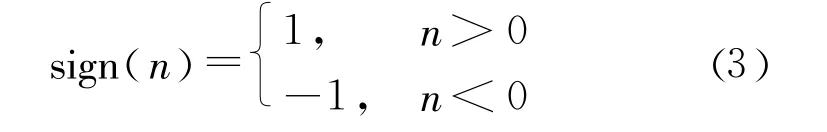
从硬阈值函数的定义可知，其处理过的小波系数在阈值处不连续，重构后的信号很可能出现局部振荡；而经软阈值函数处理过的信号，在大于阈值处估计出的信号与原始信号之间总有恒定的偏差，影响重构精度，且去噪后信号存在局部过于光滑的问题。

2 改进的阈值函数及阈值选择

为了克服软、硬阈值函数降噪的缺点，根据小波阈值降噪的原理，本文构造了一类改进的阈值函数，其表达式为：

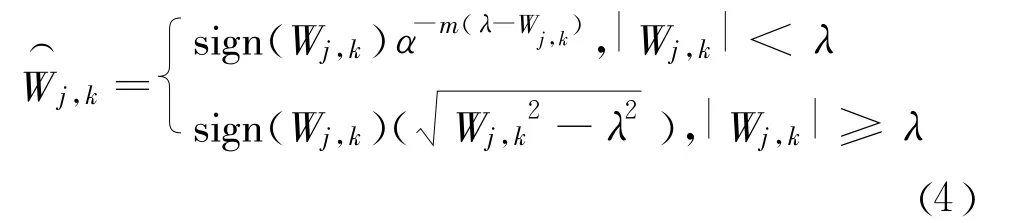
其中a（a＞0），m（m＞0）为调节因子。分别作出各阈值函数去噪示意图如图1所示，其中阈值取0.4，从图1中可以看出，硬阈值函数去噪后信号在阈值处是间断的，软阈值方法处理后的信号在大于阈值处与原信号相比，存在偏差，而改进阈值函数去噪后的信号与原信号最为接近，其克服了软、硬阈值函数去噪的缺点。

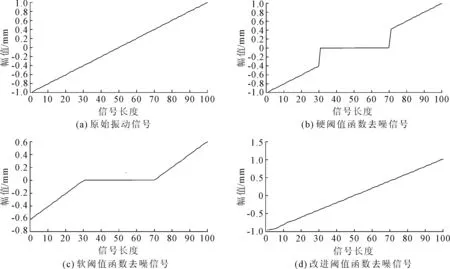
图1 各阈值函数示意图

关于阈值的选择，取的过大，不仅滤掉噪声，细节信息也可能被滤掉；而取的过小又不能完全除去噪声。由于水电机组振动信号的信噪比较小，通常采用由阈值估计风险定理确定的阈值，即固定阈值：

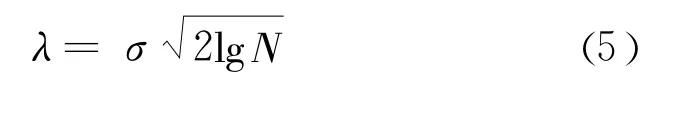
其中，N为采样信号的长度；σ为噪声标准差。

去噪效果用性噪比（SNR）和均方根误差（MSE）来衡量。若去噪后信号的性噪比提高，而均方根误差很小，则说明该阈值函数除噪不仅效果好，而且除噪后的信号与原始信号的相似度越高。SNR的定义为［1］：

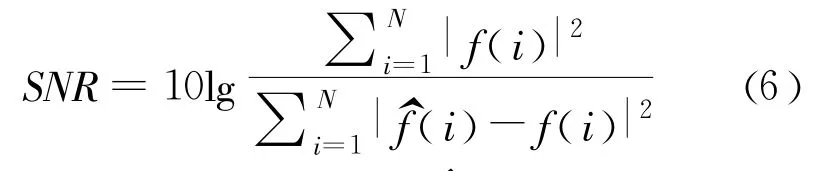
其中：f（t）为原始无噪声信号；＾f（t）为去噪后的信号；N为采样长度。

MSE的定义为：

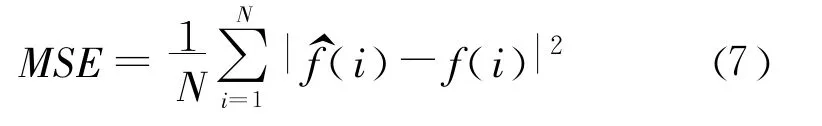
3 实例验证与分析

为了验证改进阈值函数的去噪效果，分别采用仿真信号和电厂采集信号进行去噪实验。

（1）仿真信号去噪，分别采用传统的软、硬阈值函数和改进的阈值函数对Matlab中含噪的Heavy sine和Bumps信号进行去噪实验对比，选择db4小波函数和固定阈值分解三层。

经过多次试验对比，设定 a＝3，m＝5进行计算，去噪后信号的信噪比最大，均方根误差最小，去噪效果最好，对Heavy sine和bumps信号的去噪效果分别如图2、图3所示。

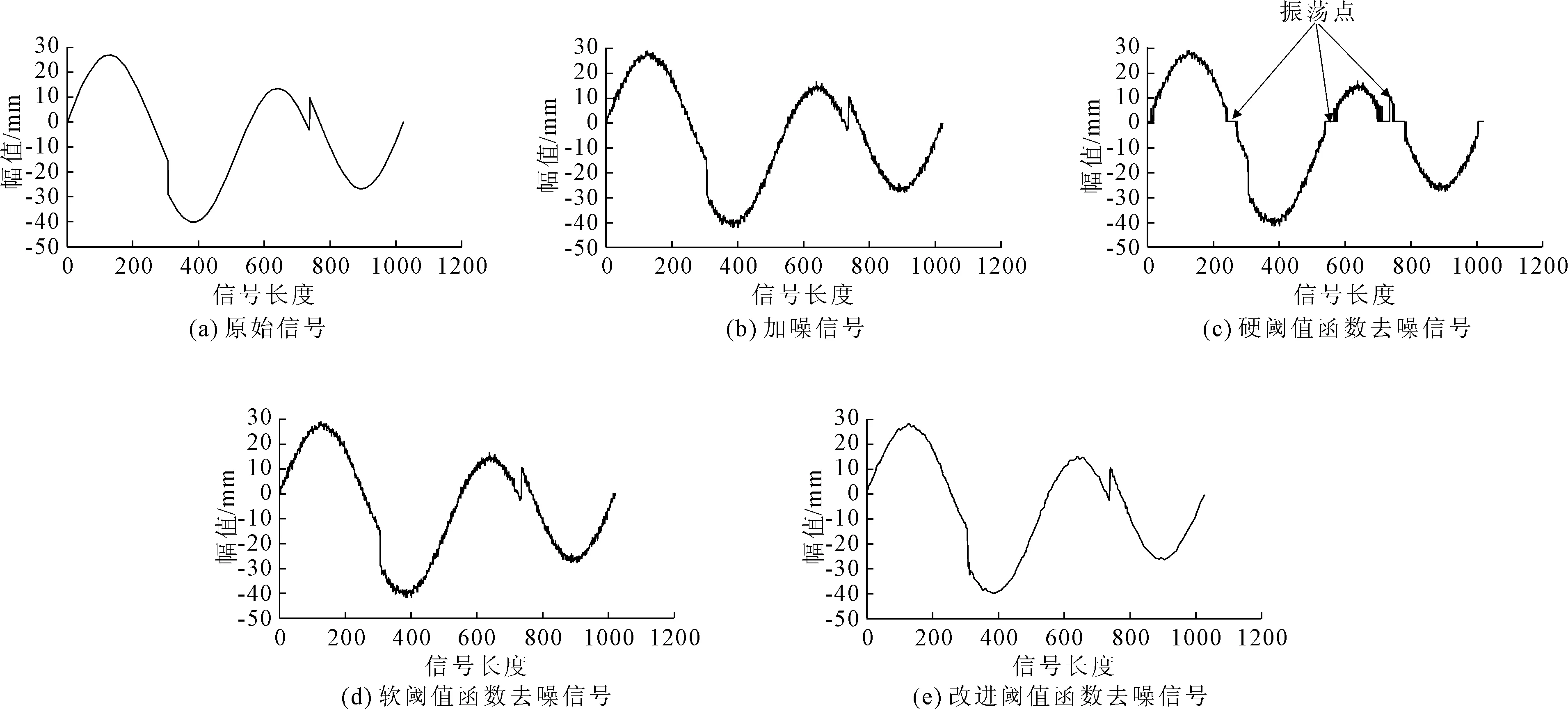
图2 各阈值函数对Heavy sine 信号的去噪图

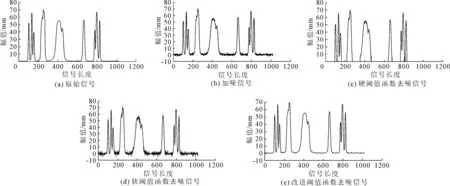
图3 各阈值函数对Bumps信号的去噪图

三种阈值函数对Heavy sine信号和bumps信号 去噪后的性噪比和均方根误差，分别见表1。

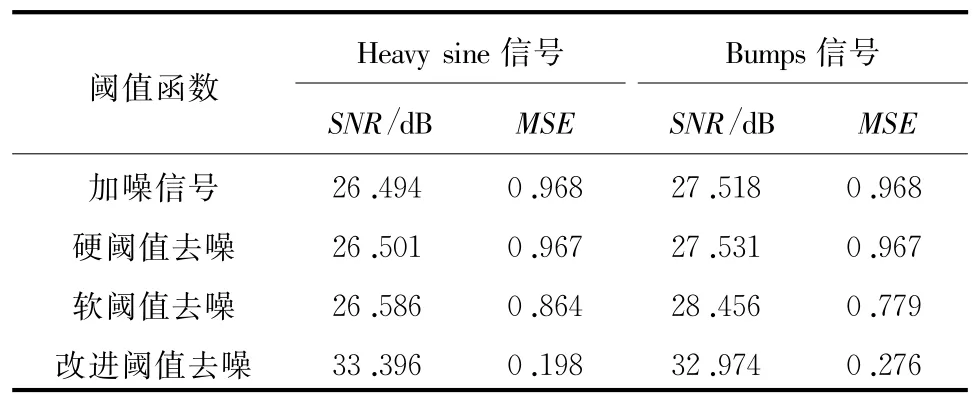
表1 Bumps信号和Heavy sine信号的SNR和MSE对比表

从图2，图3和表1中可以看出：硬、软阈值函数对Heavy sine信号和bumps信号的去噪效果一般，信噪比提高不多，且硬阈值函数降噪后存在着振荡点，软阈值函数去噪后存在明显的偏差；而改进阈值函数去噪效果很明显，不仅 SNR和MSE都有大幅度的提高；而且改进函数降噪后的波形与原始信号波形最为接近，突出了改进算法的优越性。

（3）利用实测的振动数据进行检验。某电厂为立式机组，额定转速为150 rPm，振动传感器的采样频率为200 Hz，采用db4小波函数对振动信号三层分解，三种阈值函数的去噪效果如图4所示。

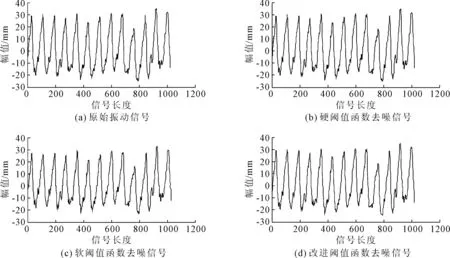
图4 振动信号的去噪效果图

从图4中可以看出，硬阈值函数有一定的去噪，但重构后信号的连续性不及原始信号；软阈值函数去噪效果虽较好，但与原波形之间存在着恒定偏差，从能量角度而言，软阈值函数降噪削弱了信号的能量；而改进阈值函数不仅消除了噪声，同时对振动波形的特征保留最好。

由于是电厂实测的含噪振动信号，无法通过性噪比公式（6）和均方根误差公式（7）衡量去噪效果，因此本文将保留突变点振动信息的能力作为评判的依据。在三种阈值函数降噪后直接读取振动信号突变点的幅值，对比其幅值与采集信号幅值的接近程度［8］。水电机组振动信号一般以（1／6～1／2）倍频、1倍频、2倍频、3倍频、50 Hz、100 Hz等频率作为故障特征频率［1］，因此对比这几个频段去噪前后幅值的差别来衡量去噪效果。

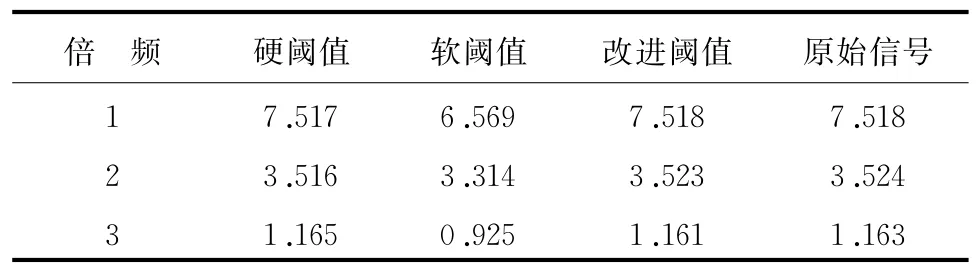
表2 降噪后频率保留程度对比

分别作出三种阈值函数降噪与电厂采集信号对比的FFT频谱图，如图5～图7所示，从图中可以看出：三种降噪方法与原始实测信号的频谱特征基本相同，但是与采集信号的频谱曲线重合度最高的是改进阈值函数去噪后所得的频谱曲线。选择降噪前后1倍频、2倍频、3倍频的幅值进行对比分析见表2，从表2可知：硬阈值函数降噪后2倍频的幅值与采集信号有一定的偏差，软阈值函数降噪后3倍频的幅值与采集信号都相差较大，而改进阈值函数去噪后信号的各个倍频的幅值最为接近采集的振动信号的幅值。

因此可以得出：与软、硬阈值降噪方法相比，改进的阈值函数降噪后振动信号各个倍频的幅值更加接近降噪前，即对振动信号特征分量的保留比软、硬阈值函数更好。

4 结 论

针对传统软、硬阈值函数去噪存在的缺点，本文提出了一种改进的阈值函数，通过仿真信号和实测振动数据的实验表明，改进的阈值函数克服了软、硬阈值去噪的缺点且去噪效果好。通过对比降噪后对振动信号特征分量的保留程度，说明改进的阈值函数是一种有效的降噪方法，具有一定的应用价值。

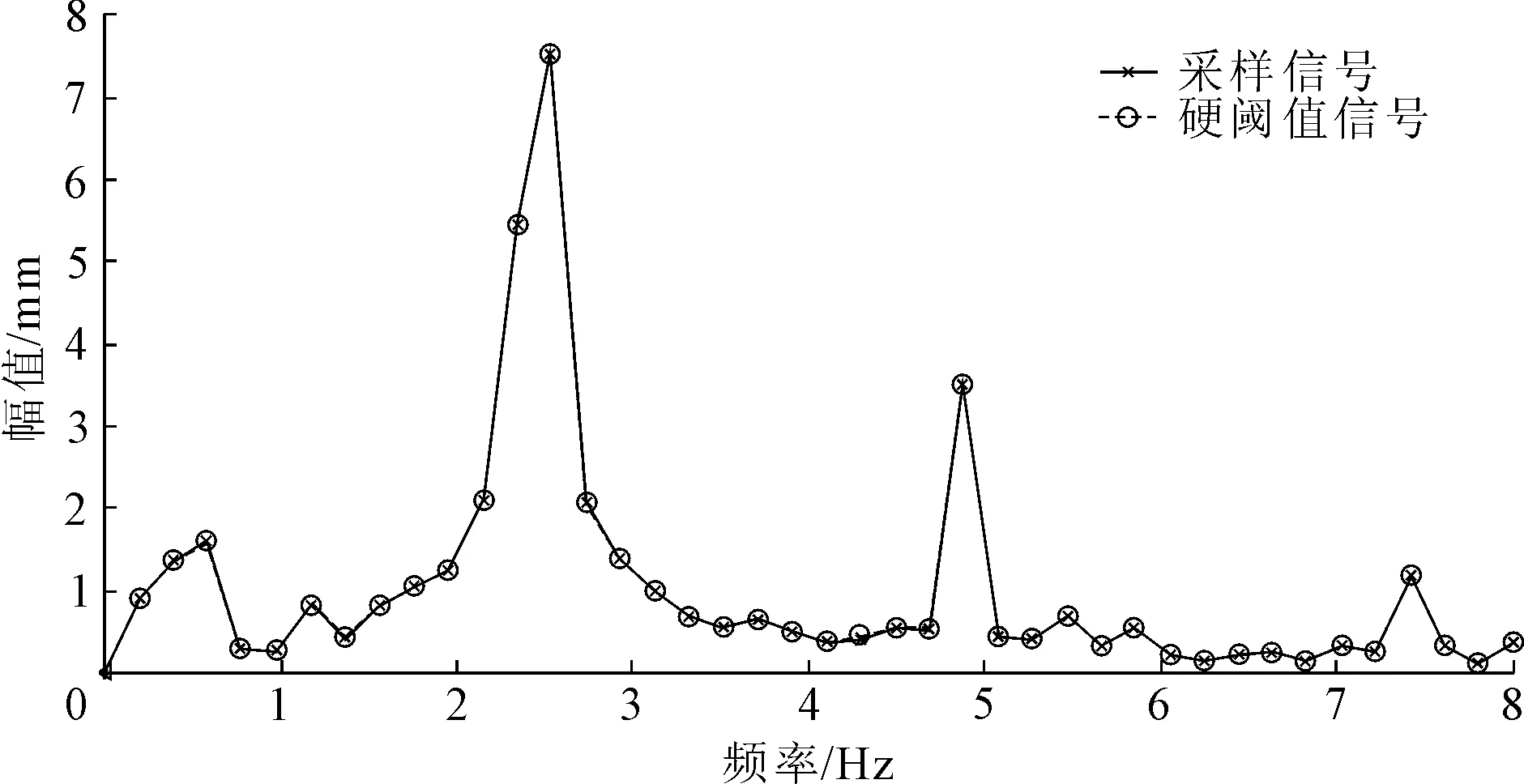
图5 硬阈值函数降噪与采样信号FFT频谱图

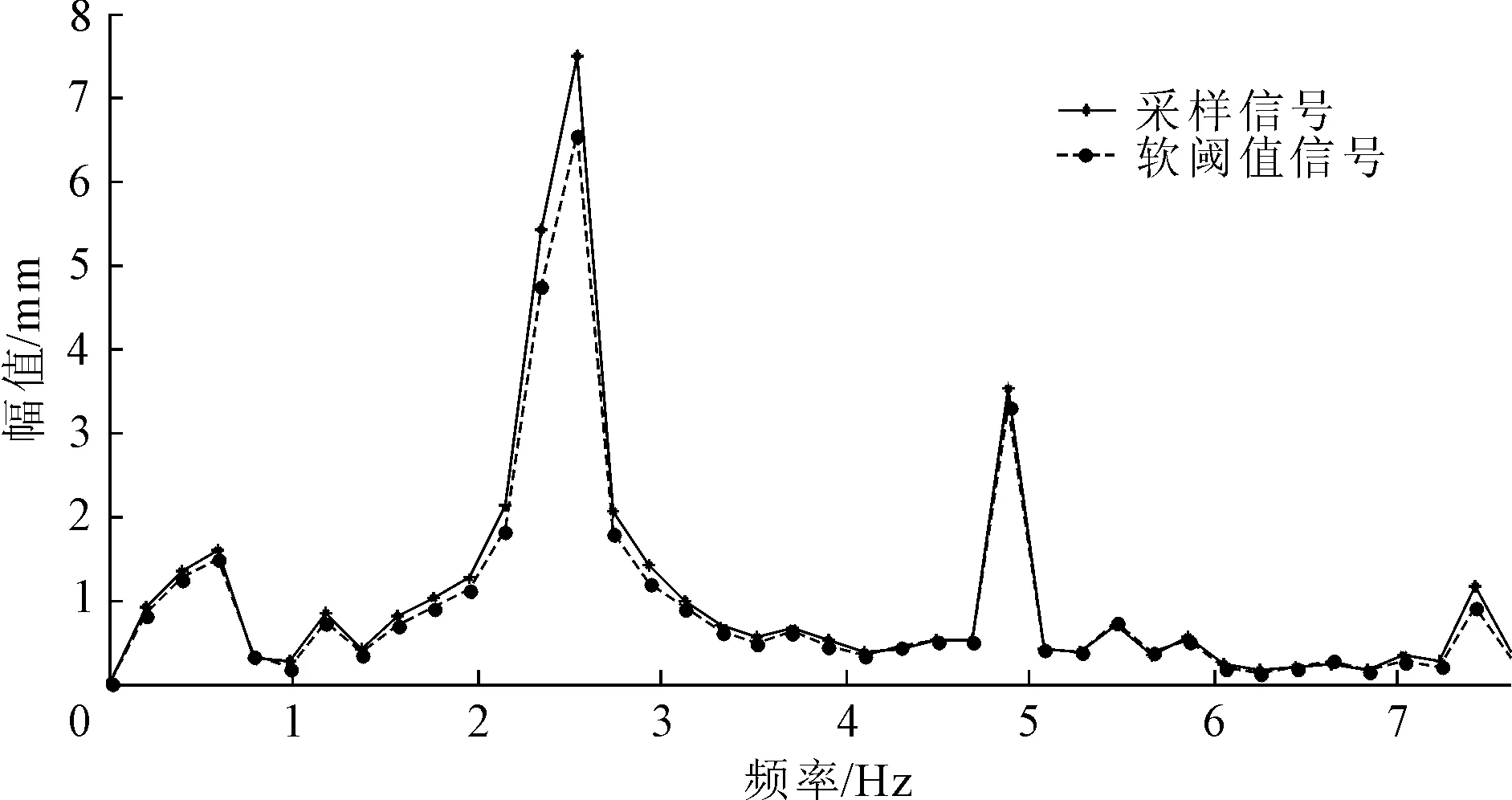
图6 软阈值函数降噪与采样信号FFT频谱图

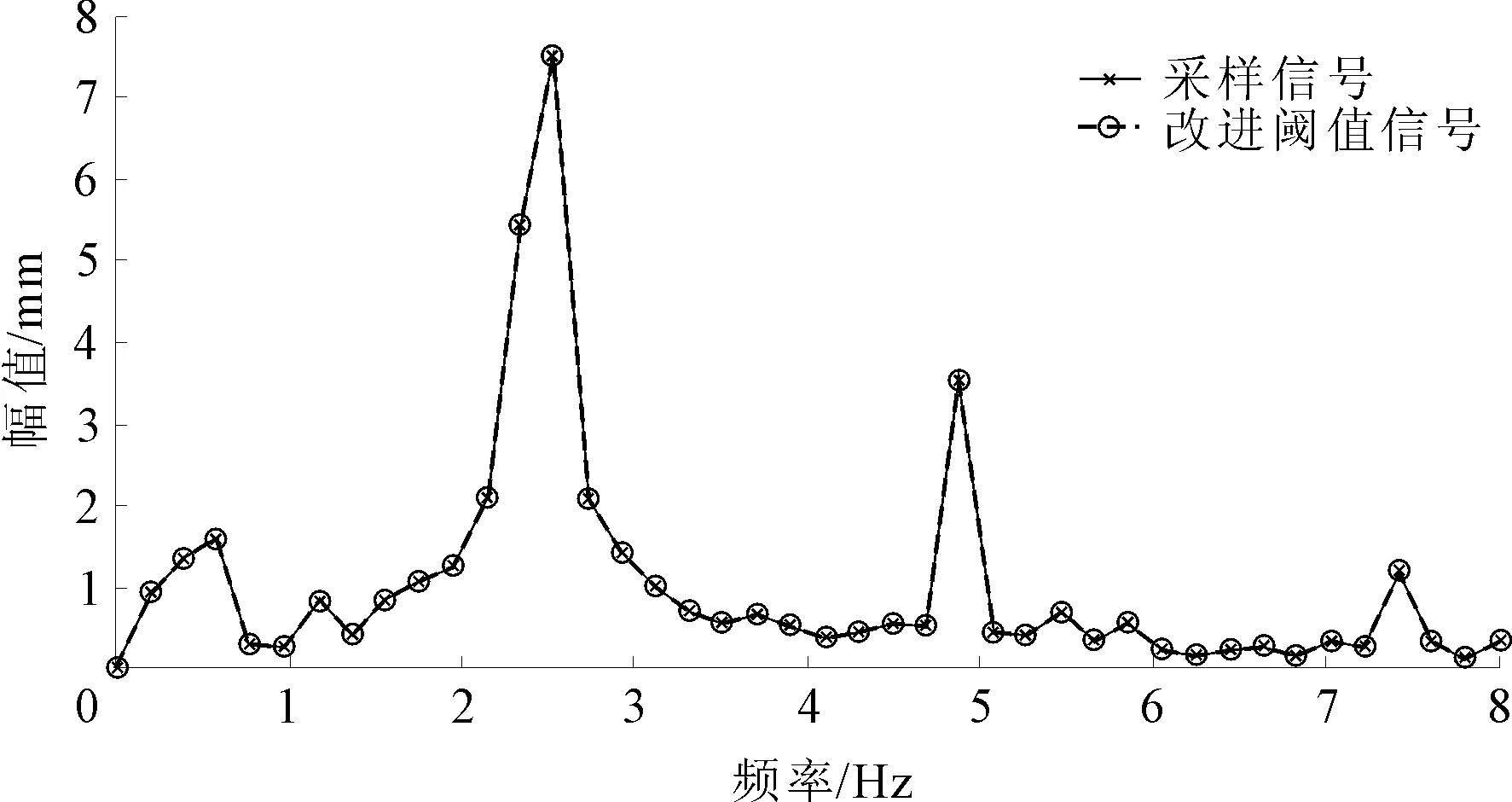
图7 改进阈值函数降噪与采样信号FFT频谱图

［1］ 苏 立，南海鹏，余向阳，等.基于改进阈值函数的小波降噪分析在水电机组振动信号中的应用［J］.水力发电学报，2012，31（3）：246－251.

［2］ 黄伟国.基于振动信号特征提取与表达的旋转机械状态监测与故障诊断研究［D］.合肥：中国科技大学，2010.

［3］ Donoho D L.De－noising by soft－thresholding［J］.IEEETrans Inform Theory，1995，41（3）：613－618.

［4］ 叶重元，黄永东.小波阈值去噪算法的新改进［J］.计算机工程与应用，2011，47（12）：141－145.

［5］ 刘 涛，曾祥利 ，曾 军.实用小波分析入门［M］.北京：国防工业出版社，2006.

［6］ 孙延奎.小波分析及其应用［M］.北京：机械工业出版社，2005.

［7］ 张德丰.MATLAB小波分析［M］.北京：机械工业出版社，2009.

［8］ 张 明，李开成 .胡益胜 .基于小波邻域阈值分类的电能质量信号去噪算法［J］.电力系统自动化，2010，32（10）：84－88.

［9］ Donoho D L，Johnstone IM.Ideal spatial adaptation by wavelet shrinkage［J］.Biometrika，1994，81（3）：425－455.

［10］ Mallt S，Zhonc S.Characterization of signals from multiscale edges［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1992，14（7）：710－732.

［11］ 唐进元，陈维涛，陈思雨，等.一种新的小波阈值函数及其在振动信号分析中的应用［J］.冲击与振动，2009，28（7）：118－121.

［12］ Zheng H，LIZ，Chen X.Cear fault diagnosis bused on continuouswavelet transform［J］.Mechanical Systems and Signal Processing，2002，16（2－3）：447－457.

［13］ Liu Feng，Ruan Xiao E.Wavelet－based diffusion approaches for signal denoising［J］.Signal Processing，2007，87（5）：1138－1146.

［14］ Donoho D L，Johnstone IM.Ideal spatial via wavelet shrinkage［J］.Biometrika，1994，81（3）：425－455.

［15］ 于文新，张 谦.基于改进阈值消噪算法的小波包降噪［J］.通信技术，2010，43（6）：7－9.

The Application of An Improved Wavelet Threshold Function in the De－noising of the Hydropower Units Vibration Signal

GAO Shu－guang
（MeixianWanjiayuan Hydropower Station，Baoji，Shaanxi722300，China）

Threshold de－noising based onwavelet is a commonly used algorithm in the de－noising of the hydropower units vibration signal.The conventional threshold functions can be divided into hard threshold function and soft threshold function.for hard－threshold function processed signal，the reconstructed signal is discontinued at the threshold，which is prone to cause additionaloscillations to the reconstructed signal；whereas the signal de－noised by soft threshold function has a better overall continuity，but there’s always a constant deviation between the reconstructed signal and the original one，which is prone to affect the reconstruction accuracy.Based on this situation，awaveletde－noising algorithm with an improved threshold functionwas broughtup in this article.TheMatlab simulationwith the actual collected data indicates that the new method overcomes the drawbacks of the conventional ones，and it has a good de－noising effect.Comparing with themaintaining level of different de－noisingmethods on the vibration signal’s characteristic components，the new method shows a better performance on each component.In summary，it’s an effective de－noisingmethod.

hydropower units；vibration signal；wavelet de－noising；threshold function

TM312

A

1672—1144（2014）04—0213—05

10.3969／j.issn.1672－1144.2014.04.043

2014－02－28

2014－04－03

高曙光（1977—），男 ，陕西太白人 ，助理工程师 ，主要从事小水电运行管理工作。