滚动机制对颗粒材料剪切带形成的影响

唐洪祥，董益峰，张 兴

（1.大连理工大学海岸和近海工程国家重点实验室 ，辽宁大连116024；2.大连理工大学土木工程学院，辽宁大连116024；3.珠海奥裕丰钢铁有限公司，广东珠海519050）

滚动机制对颗粒材料剪切带形成的影响

唐洪祥1，2，董益峰1，2，张 兴3

（1.大连理工大学海岸和近海工程国家重点实验室 ，辽宁大连116024；2.大连理工大学土木工程学院，辽宁大连116024；3.珠海奥裕丰钢铁有限公司，广东珠海519050）

从宏观角度引入颗粒集合体有效应变表述颗粒材料剪切带的形成 ，从细观上模拟颗粒材料自由滚动、限制滚动、考虑滚动机制三种情况在外荷载下的力学响应。通过分析追踪颗粒材料有效应变的变化，探讨了颗粒材料剪切带的发展和形成过程。结果表明：限制滚动下不能模拟剪切带的发展，考虑颗粒自由滚动及滚动机制能较好的模拟剪切带的发展。而强调滚动机制限制了次要剪切带，同时促进主要剪切带的发展，因而能更有效的描述剪切带的形成过程。

颗粒材料；滚动机制；剪切带；有效应变

颗粒材料如密实的砂土等在外荷载作用下，常出现变形集中于局部区域逐渐发展，并最终导致材料整体失稳破坏的现象，这个变形集中的局部区域常称为剪切带。剪切带的出现是材料失稳与破坏的前兆，学者们对其的形成机理等广泛关注［1］。

离散元从细观角度通过颗粒间的相互作用、颗粒位置以及颗粒转角等信息分析颗粒集合体的力学特性，这使得其各项参数的物理意义明确，虽然本构简单，但却能从细观角度很好的描述宏观力学行为的细观机理。Iwashita K和Oda M等［2－5］最早使用离散元对剪切带进行分析。Proubet J等［6］采用柔性应力边界，分析颗粒材料剪切带内位移。周健等［7－10］总结离散元的分支 －颗粒流在岩土工程中的应用。在实验上，Desues J和Barden L等［11－12］研究了砂土在三轴实验条件下剪切带的形成和发展。TakahashiM等［13］实验研究了砂土的微结构变形 ，并给出了剪切带的倾角、厚度等信息，而要较好地模拟颗粒材料这些现象，应在颗粒间的接触关系中考虑引入滚动机制。蒋明镜［14］、楚锡华［15］等也指出强调滚动机制对模拟颗粒材料剪切带的形成有重要作用，并对颗粒材料的抗剪强度等有较大的影响。

本文通过离散单元模型，考虑滚动机制的影响，结合宏观上剪切带形成和发展的描述，分析颗粒材料在双轴压缩过程中的特性。为直观地表述剪切带的形成过程，从宏观的角度引入易于理解和接受的颗粒集合体的有效应变定义，通过选取不同的影响颗粒滚动的参数值，在细观上模拟颗粒材料在颗粒自由滚动、考虑滚动机制、限制颗粒滚动情况下颗粒材料的细观力学响应、有效应变及转角的变化，从而研究压缩过程中剪切带出现和发展的细观机理。在此基础上，来说明引入滚动机制对模拟颗粒材料的重要性。

1 考虑附加滚动机制的离散元模型

本文采用的离散元模型基于文献［5，8］的改进离散元模型，其中颗粒间接触作用采用了图1中法向作用、切向作用以及滚转三种方式的组合。

图1 颗粒间相互接触作用情况

结合图1，相邻两颗粒间的接触作用可以表示为公式（1）：

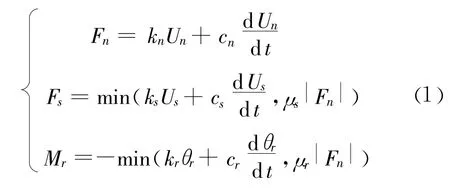
式中：Fn、Un、kn、cn分别为颗粒间的法向作用力、法向位移、法向接触刚度、法向阻尼系数；Fs、Us、ks、cs、μs分别为颗粒间的切向作用力、切向位移、切向接触刚度、切向阻尼系数、切向滑动摩擦系数；Mr、 θr、kr、cr、μr分别为颗粒间的力矩、滚转角、切向滚动阻力刚度系数、切向滚动阻尼系数、切向滚动摩擦系数。

2 颗粒的名义应变

图2 不同时刻颗粒位置示意图

如图2所示，t1、t2时刻颗粒A、B空间位置的差为：

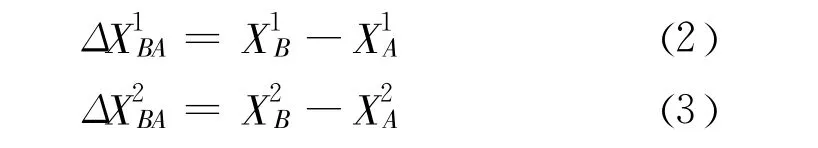
若参考局部坐标系，则：

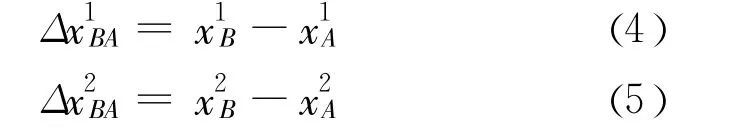
通过坐标变换：

然后，t1时刻的局部坐标系先绕y1轴旋转角度，再绕z1轴旋转角度，同样的，t2时刻的局部坐标系先绕y2轴旋转角度 ，再绕z2轴旋转角度，则：

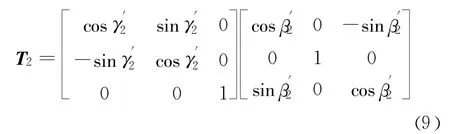
颗粒A与颗粒B中心位置的相对变化可以用变形梯度 f来描述，对变形梯度进行极分解：

其中R为代表颗粒转动的正交张量；U为代表拉伸变形的正定对称张量：

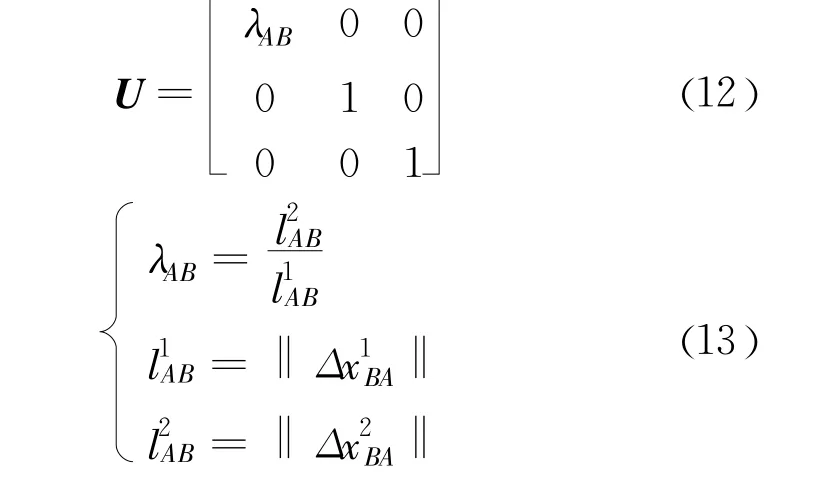
根据颗粒A和B在t1与t2时刻的位置关系定义有效体积应变定义为：

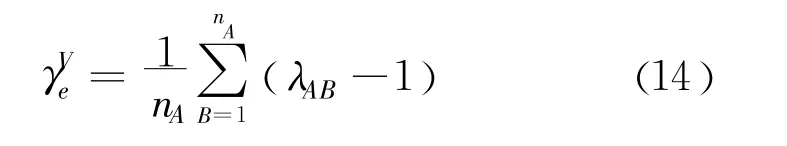
式中，nA为与颗粒A相接触的颗粒的个数。联立式（6）～式（9）得：

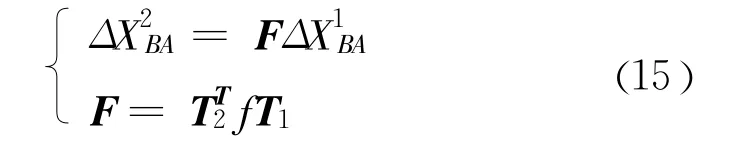
系定义位移导数张量：

式中 I表示单位阵，令 Dij为D的分量，定义：

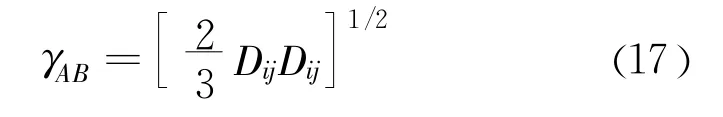
由式（17）可以定义颗粒A中心处的有效应变γe：

其中 nA为与颗粒A相邻颗粒个数。对于二维情况，相应的 T1，T2，R，U矩阵可退化为二维，从而得到平面状态下颗粒的名义应变。

3 颗粒材料的双轴压缩试验

3.1 模型的生成

使用4 950个半径为5mm的颗粒生成86.7 cm ×50 cm的模型，模型的孔隙率为0.0931，上下对称的刚性板施加轴向的位移荷载。试样如图3所示，在压缩过程保持左右两侧围压 σ3＝0.1 MPa恒定，颗粒离散元模拟所需的材料参数如表1所示。

图3 双轴压缩数值模型

表1 数值模拟参数

3.2 颗粒自由滚动

对于自由滚动，颗粒间的滚动不受到任何约束，与滚动相关联的切向滚动阻力刚度系数 kr＝0 Nm／rad，切向滚动阻尼系数 cr＝0 Ns／m和切向滚动摩擦系数 ur＝0，这种情况相当于常规的采用滑动模型的离散元模型。由计算得到的轴向应力与应变的关系曲线见图4。图5为不同轴向应变下颗粒的有效应变图。可见，在应力应变曲线的峰值前，剪切带沿双轴试样的对角线方向开始发展（见图5（b））；在应力应变曲线的峰值后的一段变形内，沿双轴试样的对角线方向较快地形成交叉的完整的剪切带（见图5（c））；随后，试样变形集中于剪切带内发展，如图5（d）与图5（c）的剪切带宽度差不多，但前者有效应变值大得多。

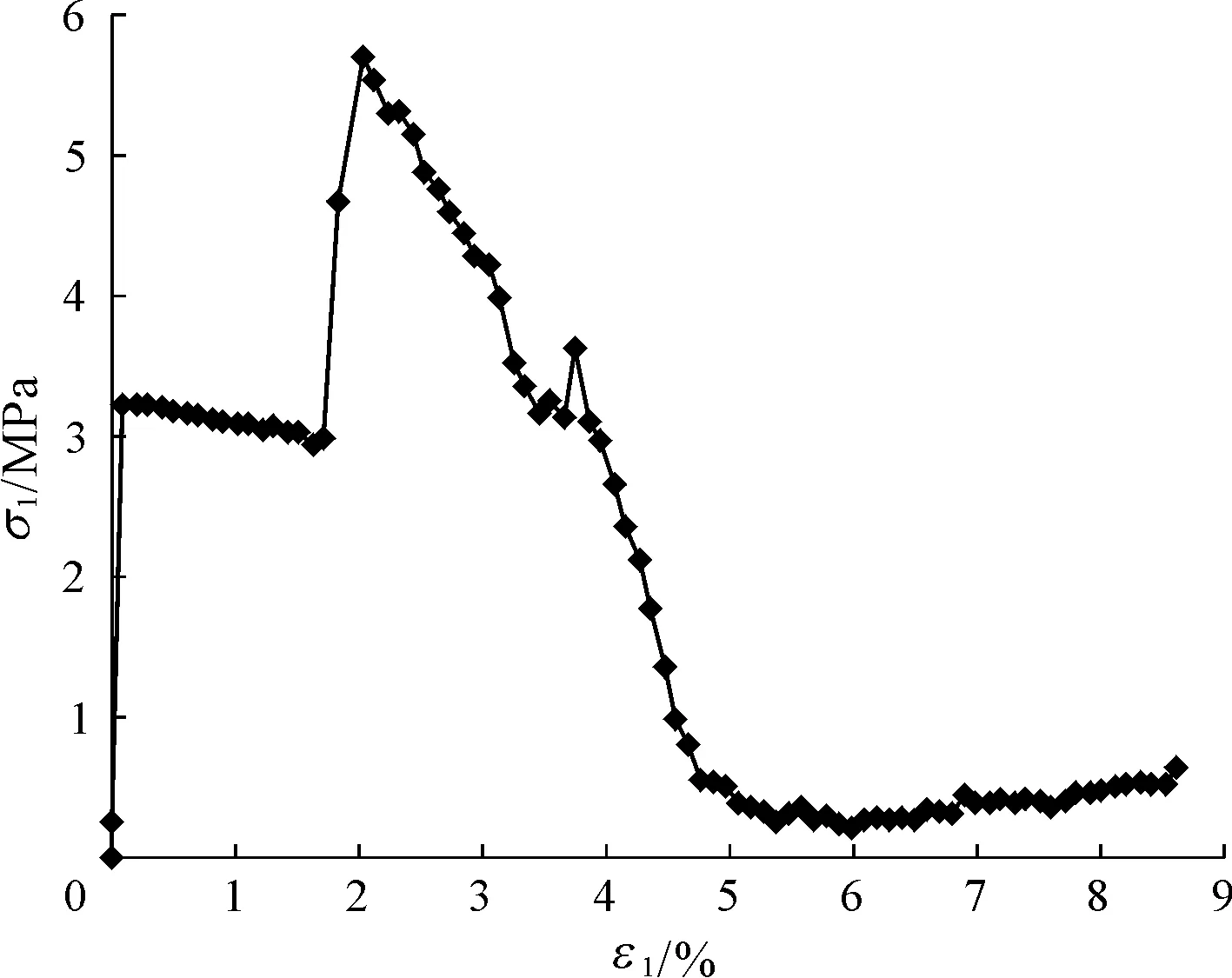
图4 自由滚动情况下模型的轴向应力—应变图

图5 自由滚动情况下模型的有效应变图

3.3 考虑滚动机制

在此情况下，kr＝1.0×106Nm／rad，cr＝0.1 Ns／m，ur＝0.1。这使得颗粒在法向约束和切向滑动约束的基础上，多了一个切向滚动的约束，即滚动发生的门槛值。图6给出了颗粒模型的轴向应力和应变关系，可见峰值荷载比自由滚动情况下要高一些，但出现的轴向应变值差不多。图7为不同轴向应变下颗粒的有效应变图，可见随着轴向位移的增加可以观察到与图5类似的剪切带发展规律；与图5相比，可见本部分强调滚动机制下可观察到更加明显的剪切带，且剪切带的宽度变窄。由此可见，为了更好的模拟剪切带的发展，需在离散元数值模型中考虑滚动机制的影响。

3.4 限制颗粒滚动

在此情况下，与颗粒滚动相关的参数都取一个很大的值，kr＝1×108N／m，cr＝1.0 Ns／m，ur＝1.0，这使得颗粒滚动受到很大约束，颗粒几乎不能转动。轴向应力与应变关系曲线如图8所示，可见，在峰值荷载附件曲线波动较大，这可能是由于限制了颗粒的滚动使得其难以平缓运动所致；与前面两种情况相比，峰值荷载较高且所在的应变后移，这是因为要使颗粒移动需要更大的外荷载和更大的变形量。图9为不同轴向应变下颗粒的有效应变图，从图9中看不到明显的剪切带，究其原因，此种情况下的颗粒间约束较强，发生相对移动困难。

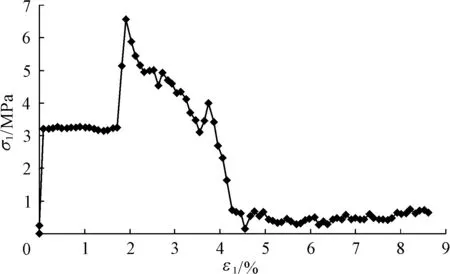
图6 滚动机制情况下模型的轴向应力—应变图

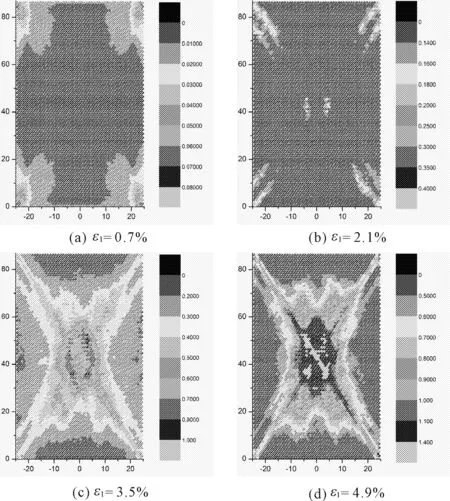
图7 滚动机制情况下模型有效应变图

4 结 论

为直观地表述剪切带的形成过程，本文从宏观的角度引入易于理解和接受的颗粒集合体的有效应变定义，通过细观上模拟颗粒自由滚动、考虑颗粒滚动机制以及颗粒限制滚动情况下的力学响应，分析追踪了有效应变在颗粒材料中的发展变化，以此探讨了颗粒材料剪切带发展和形成过程的细观机理，说明了在颗粒材料剪切带模拟中引入滚动机制的必要性。限制颗粒滚动下不能模拟剪切带的发展，考虑颗粒自由滚动及滚动机制能较好地模拟剪切带的发展。而强调滚动机制限制了次要剪切带，同时促进了主要剪切带的发展，因而能更有效地描述剪切带的形成过程。

图8 限制滚动情况下模型的轴向应力—应变图

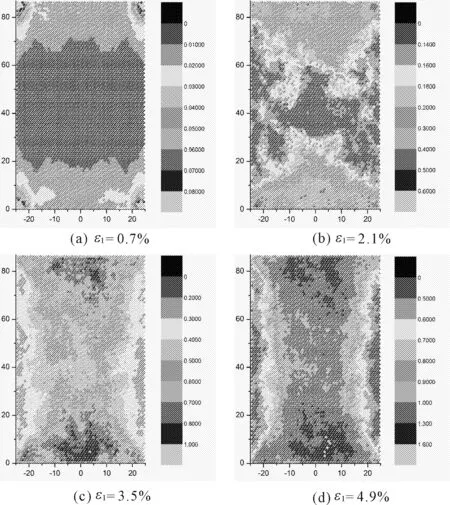
图9 限制滚动情况下模型的有效应变图

［1］ 赵锡宏，张启辉.土的剪切带试验与数值分析［M］.北京：机械工业出版社，2003.

［2］ Iwashita K，OdaM.Rolling resistance at contacts in simulation of shear band developmentby DEM［J］.Journalof EngineeringMechanics，1998，124（3）：285－292.

［3］ OdaM，Kazama H.Microstructure of shearbands and its relation to the mechanisms of dilatancy and failure of dense granular soils［J］.Geotechnique，1998，48（4）：465－481.

［4］ Iwashita K，Oda M.Mechanics of Granular Materials［M］.CRC Press，1999.

［5］ Iwashita K，Oda M.Micro－deformationmechanism of shear banding process based on modified distinct elementmethod［J］.Powder Technology，2000，109（1）：192－205.

［6］ Bardet JP，Proubet J.A numerical investigation of the structureof persistent shearbands in granularmedia［J］.Geotechnique，1991，41（4）：599－613.

［7］ 周 健，池 勇 ，池毓蔚，等 .颗粒流方法及PFC2D程序［J］.岩土力学，2000，21（3）：271－274.

［8］ Zhou Jian，ChiYong.The application of particle flow code in Geotechnical Engineering［J］.Geotechnical Engineering，2002，14（2）：1－4.

［9］ 周 健，池毓蔚，池 永，等.砂土双轴试验的颗粒流模拟［J］.岩土工程学报 ，2000，22（6）：701－704.

［10］ 周 健，池 永.砂土力学性质的细观模拟［J］.岩土力学，2003，（24）：901－906.

［11］ Desues J，Chambon R，MokniM，et al.Void ratio evolution inside shear bands in triaxial sand specimens studied by computed tomography［J］.Geotechnique，1996，46（3）：529－546.

［12］ Barden L.Incremental strain rate ratios and strength of sand in the triaxial test［J］.Geotechnique，1966，16（4）：338－357.

［13］ TakahashiM，Takemura T，OdaM.Microstructure in shear band observed bymicrofocus X－ray computed tomography［J］.Geotechnique，2004，54（8）：539－542.

［14］ Jiang M J，Yu H S，Harris D.A novel discretemodel for granularmaterial incorporating rolling resistance［J］.Computers and Geotechnics，2005，32（5）：340－357.

［15］ 楚锡华.颗粒材料的离散颗粒模型与离散－连续耦合模型及数值方法［D］.大连：大连理工大学，2007.

The Effects of Rolling Resistance on the Formation of Shear Bands for Granular Materials

TANG Hong－xiang1，2，DONG Yi－feng1，2，ZHANG Xing3
（1.The State Key Laboratory of Coastal and Offshore Engineering，Dalian University of Technology，Dalian，Liaoning 116024，China；2.School of Civil and Hydraulic Engineering，Dalian University of Technology，Dalian，Liaoning 116024，China；3.ZhuhaiYueyufeng Steel Co.，Ltd.，Zhuhai，Guangdong 519050，China）

Themacroscopic definition of effective strain was introduced to describe the emergence and development of shear bands in granularmaterials.Three differentnumerical tests（i.e.，free rolling test，limiting rolling testand rolling resistance considered test）using the discrete elementmethod（DEM）were conducted to simulate themechanical response of granular specimens under stress.The progressive development of effective strain in the granular specimenswas illustrated to analyse the origination and evolution of shear bands.The results indicate that the evolution of shear bands in granularmaterials can be simulatedmore accurately in free rolling and rolling resistance considered tests，while be hardly simulated when particle rolling is strictly prevented.In the caseof particle rolling resistance，the shear band evolution is more distinct as the evolution of theminor shear bands is limited while themajor shear bands are preferably promoted.

particlematerials；rolling resistance；shear bands；effective strain

TU411.7

A

1672—1144（2014）04—0107—05

10.3969／j.issn.1672－1144.2014.04.020

2014－02－24

2014－05－21

国家重点基础研究发展规划（973）项目（2010CB731502）以及中央高校基本科研业务费专项资金项目资助

唐洪祥（1973—），男 ，湖北天门人 ，博士 ，副教授，主要从事岩土力学方面的研究。