一种薄层接触单元的开发及 FLAC3D实现
2014-07-07刘莹骏张运良
刘莹骏,张运良
(大连理工大学建设工程学部,辽宁大连116024)
一种薄层接触单元的开发及 FLAC3D实现
刘莹骏,张运良
(大连理工大学建设工程学部,辽宁大连116024)
随着土木水利行业的蓬勃发展 ,出现越来越多岩土 -结构相互作用的问题。虽然目前国内外学者研究出很多种类的接触面本构模型,但大多软件中的接触面模型甚为简单,如此便限制了软件对接触面问题的模拟。FLAC3D软件中的interface单元是简单的库伦滑移型无厚度接触单元 ,不能模拟接触面所能表现出的例如应变软化等特性。鉴此,基于塑性力学,首先提出了一种弹塑性本构模型。然后基于VC++语言,将此模型开发成适用于FLAC3D软件的薄层实体单元。最后用三个数值算例验证了所开发的单元和本构模型能反映接触面在弹性阶段的非线性 ,在塑性阶段的应变软化、大变形、法向剪胀及拉伸破坏等特性。用所开发的新单元代替原有的interface单元能提高FLAC3D模拟复杂接触特性的能力。
接触面;薄层实体单元;弹塑性本构模型;FLAC3D;VC++语言
岩土-结构接触面的数值模拟,根据单元配置的不同大体可分为三类:基于接触力学的接触单元,剪切界面单元和薄层实体单元[1-6]。这三类单元各有其优缺点,并都有成功应用的实例。接触力学单元通过拉格朗日法和罚函数法能模拟刚体或连续体之间的接触与滑移,并被多个商业软件如MARC和ANSYS等采用。剪切界面单元能够合理模拟岩土-结构具有很薄接触面的法向和切向应力-应变关系,并可退化至无厚度的Goodman单元。薄层实体单元与普通单元具有相同的单元格式,这种单元和附近其他材料单元有很好的兼容性。有些情况下,接触面的滑移可能不是沿着接触面,而是发生在离接触很近的土体中(即形成了剪切带),此时薄层实体单元具有更好的适应性。Sharma和 Desai(1992)[7]对界面和节理的模拟证实了这一点,发现薄层实体单元比剪切单元更趋近于收敛解。近年来,关于薄层单元的研究受到了广泛关注。
当前,数值分析软件采用的接触面模型大多比较简单。例如,广泛应用于岩土工程领域的FLAC3D软件仅提供了一种基于库伦摩擦型本构关系的无厚度界面(interface)单元,此单元无法模拟许多复杂接触特性,如本构关系在弹性阶段的非线性、塑性阶段的应变软化等。本文拟基于FLAC3D软件平台开发薄层实体单元,作为对interface单元的补充,并进一步提高该软件模拟复杂接触面特性的能力。FLAC3D软件可通过两种方式进行新单元的开发。第一种方法是利用软件自带的FISH语言,如Wu(2011)[8]、Arad(2011)[9]等人的工作。然而,他们基于无厚度interface单元,并没有改进其固有的缺点。另一种方法是基于VC++语言进行编程开发。一些学者用此种办法已开发了岩土材料的本构模型[10-12],但并未涉及接触面。值得指出的是,利用FISH语言改进接触面模型的做法缺点很明显:不同的实例中,用于接触面模型的FISH语言命令流段需要全部修改,工作量大且不具通用性。利用VC++语言开发的接触单元可以无缝链接到FLAC3D软件中,作为一种新型内置单元模型进行调用,具有方便快捷易用的优点。
本文拟基于VC++语言开发一种薄层实体单元,以模拟接触面剪切方向上的非线性弹性,大变形,应变软化,以及法向的剪胀和拉伸破坏特性,并将之作为一种新单元类型嵌入FLAC3D软件中,其有效性通过三个数值算例进行了验证。
1 薄层单元本构关系
1.1 非线性弹性
在图1所示的局部坐标系x′y′z′中,具有厚度 t的薄层实体接触单元的增量应力 -应变关系可表示为[6]:
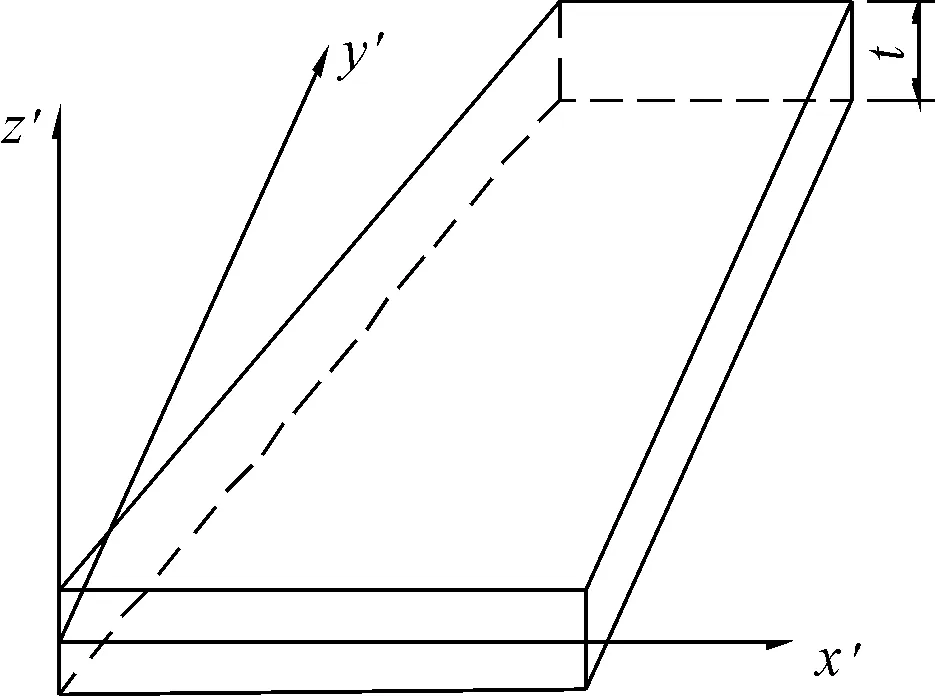
图1 薄层接触面单元
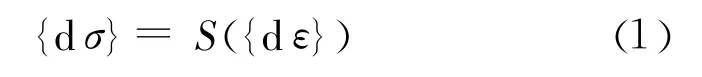
式中:S是弹性应力增量矢量{dσ}与应变增量矢量{dε}之间的关系式,即
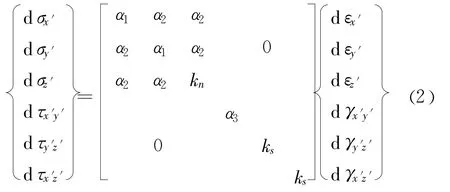
式中,α1=K+4/3G,α2=K-2/3G,α3=G,K和G分别为单元的体积模量和剪切模量。下面分别介绍单元法向刚度 kn,以及切向刚度 ks。
(1)单元法向刚度 kn。法向刚度与位移关系采用Bandis(1983)用于描述岩石节理的双曲线模型[13],法向刚度可表为:
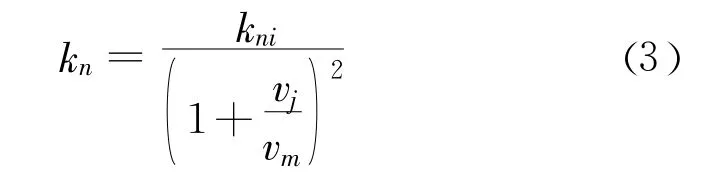
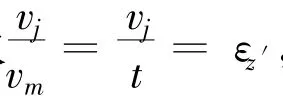
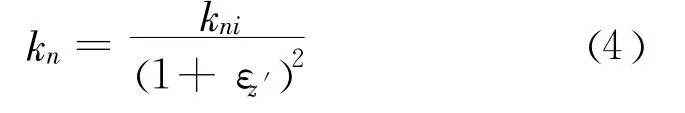
上式反映了接触面法向刚度 kn随接触面的闭合量增大而增大的关系。当接触面的闭合量趋近于接触面厚度t,也即εz′趋近于-1时,法向刚度趋近于无穷大,从而可以有效地避免接触面两侧单元的嵌入。
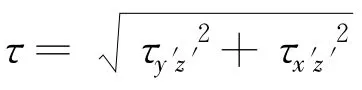
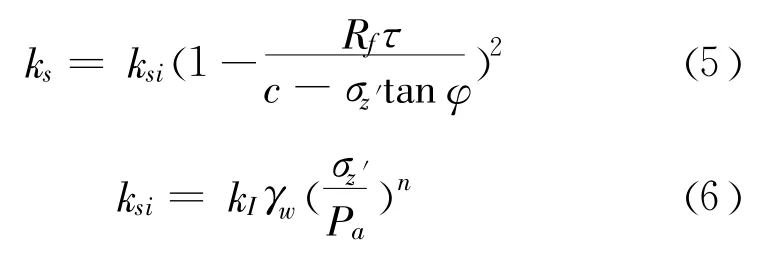
式中:,kI是无量纲刚度系数;n是刚度指数;c为单元粘聚力;φ为内摩擦角;Rf是破坏比,这些参数都可以由试验确定;γw是水的重度。
1.2 塑性表达式
1.2.1 屈服准则
采用带拉伸截断的摩尔 -库伦屈服准则[15],如图2所示。屈服准则可由σz′和τ确定的平面来描述,即f(σz′,τ)=0。从A点到B点的屈服面由摩尔-库伦屈服准则 fs=0定义:
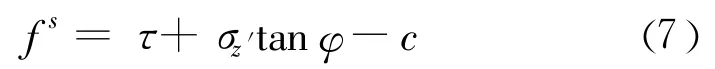
从B点到C点的屈服面则由拉伸屈服准则ft=0定义:

式中:σt是接触面的抗拉强度。理论上,抗拉强度最大值为:

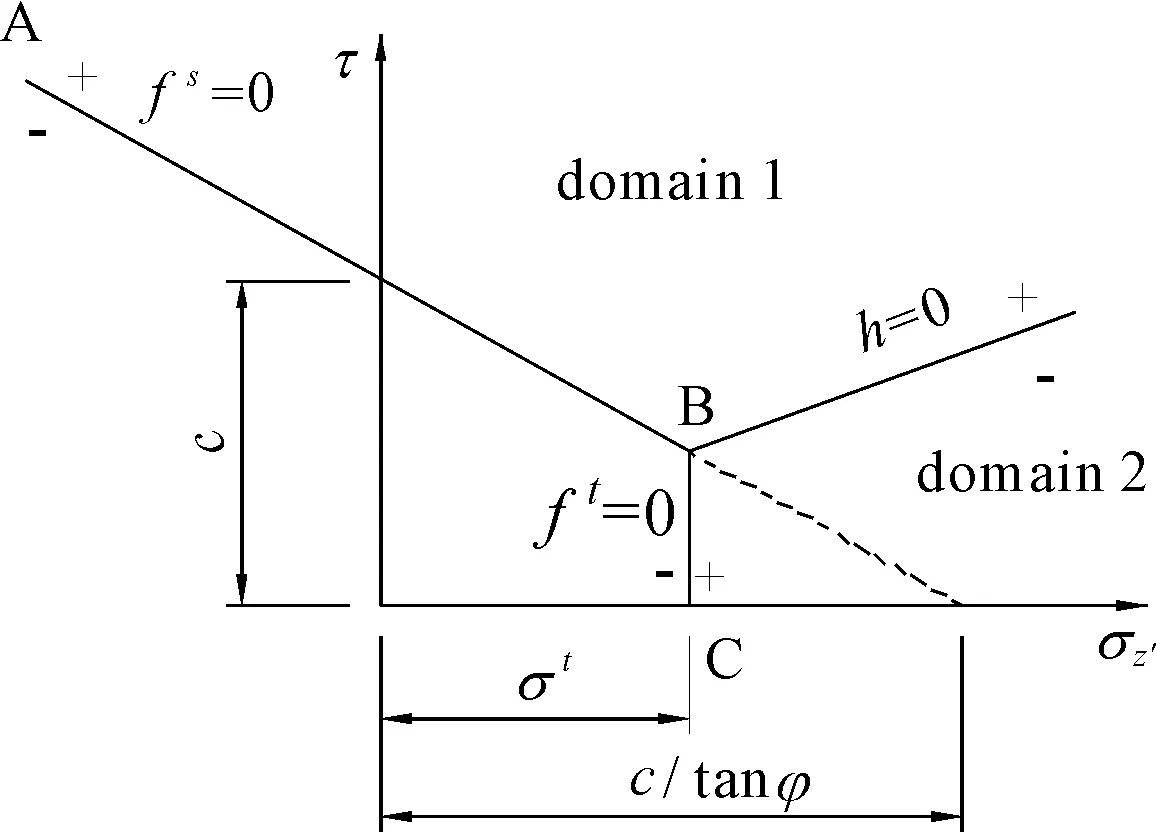
图2 带拉伸截断的摩尔 -库伦屈服准则
1.2.2 塑性势函数和流动法则
塑性势函数由一个定义剪切塑性流动的函数gs和一个定义拉伸塑性流动的函数gt组成。为了描述接触面的剪胀性,采用非关联的流动法则定义剪切势函数[15]:
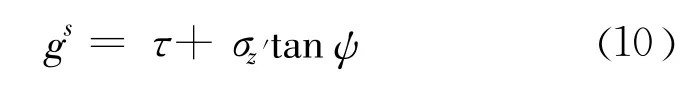
式中ψ是接触面的剪胀角。拉伸势函数采用相关联的流动法则[15]:

图2中,沿fs=0和 ft=0两条直线所形成角的对角线做一条直线h=0将塑性区划分为两个区域:剪切塑性区(domain 1)和拉伸塑性区(domain 2)。剪切塑性势函数 gs适用于剪切塑性区,而在拉伸塑性区需使用拉伸塑性势函数 gt。这条直线的表达式如下[15]:
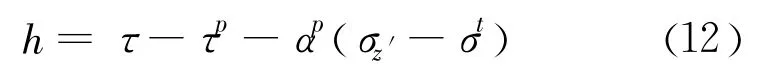
式中τP和αP是两个常数,表达式如下:
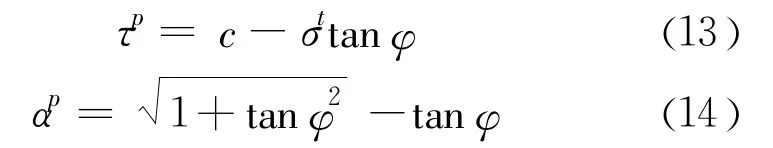
1.2.3 软化参数
本文所提出的模型能反映接触面在屈服后的应变软化现象。剪切应力τ在接触面屈服时达到峰值τp,然后随相对剪切位移δ的增加而逐渐减小,直到减小为残余剪切应力τr,如图3所示。

图3 带软化段的接触面应力变形特性
本文采用与塑性剪切应变有关的软化参数 κs来反映接触面的软化特性[15]。在进入塑性阶段后,单元的粘聚力、内摩擦角随此参数而变化。对于计算中的某一时步 Δt内,接触面单元的剪切软化参数增量 Δκs定义为关于塑性剪切偏应变增量的第二不变量的平方根:
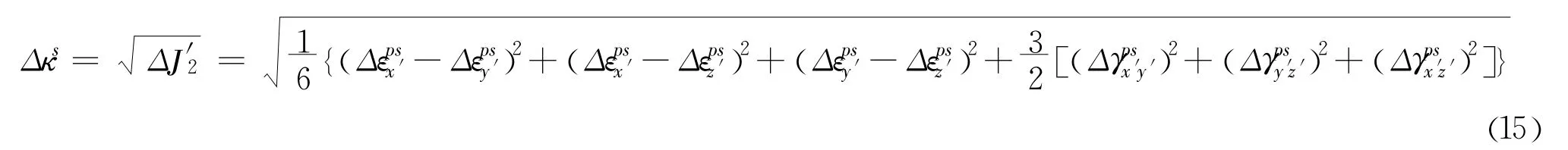
则接触单元在此步之前所累积的剪切软化参数为:

内摩擦角的变化采用由Mohamed等(2011)提出的曲线。内摩擦角可以表示为峰值内摩擦角 φp、残余内摩擦角φr、塑性相对剪切位移δp和塑性相对剪切残余位移 δrp所构成的如下关系式[9]:
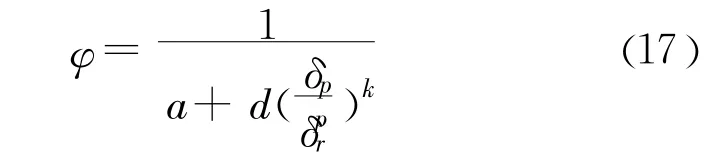
式中:
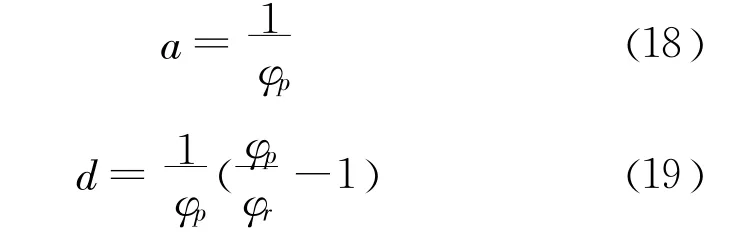
塑性相对剪切位移δp和剪切软化参数κs之间的关系可以表示为

式中:t为接触面单元的厚度。将式(20)代入式(17),有:
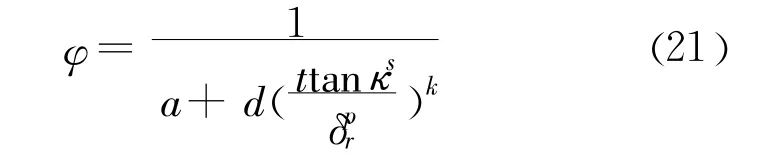
粘聚力 c由cp降至cr可采用如下线性函数:
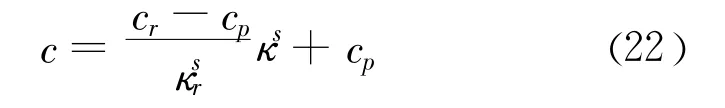
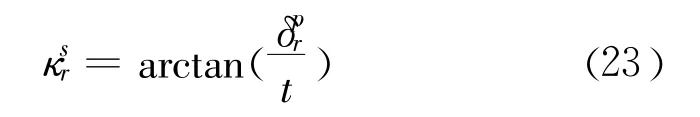
将式(23)代入式(22),有:
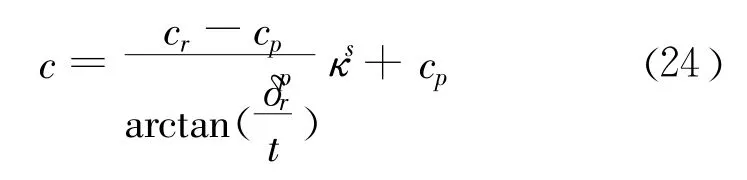
1.3 参数确定
接触面内摩擦角φ和粘聚力c可以由接触面直剪试验确定。刚度系数kI、刚度指数 n和破坏比Rf,可以做一系列不同法向压力下的接触面直剪试验,得到剪切应力 -相对剪切位移曲线,由此曲线得到不同法向压力下的接触面初始剪切刚度 ksi,再由初始剪切刚度确定 kI和n的值,最后通过比较试验所得剪切应力 -相对剪切位移曲线和由式(5)及式(6)计算的剪切应力 -相对剪切位移曲线,调整确定破坏比 Rf的值。接触面初始法向刚度 kni可以由接触面单轴压缩试验确定。接触剪胀角 ψ可以由接触面的三轴剪切试验得到,接触面抗拉强度σt一般情况下可以取为零,此值也可由接触面单轴拉伸试验确定。
在缺少试验资料的情况下,接触面的参数可由经验确定,其中切向刚度可由式(5)确定。设接触面两侧刚度较小的一侧岩土体体积模量为 K′、剪切模量为G′。在静力计算中,接触单元的剪切模量 G=0.1G′~5G′,体积模量K=0.1K′~5K′,初始法向刚度kni=0.1(K′+4/3G′)~5(K′+4/3G′),初始切向刚度ksi=0.1G′~5G′,在动力计算中,则可取接触面单元的剪切模量G=G′~20G′,体积模量K=K′~20K′,初始法向刚度kni=(K′+4/3G′)~20(K′+4/3G′),初始切向刚度 ksi=G′~20G′。
厚度 t的取值受很多因素的影响,如接触面的粗糙度、岩土体的颗粒级配、密度,可以由试验和数值计算确定。试验方面,利用改进的单剪仪[16],确定出剪切错动带的厚度h,使t在0.01B~0.1B(B是接触面单元的最小宽度)范围内趋近于 h;数值方面[17],在0.01B~0.1B范围内取几个试算t值,对模型进行网格划分,将试算结果与实测值进行比较,选择与实测结果接近的对应厚度作为 t的估值。
2 本构关系差分算法
FLAC3D中单元应力、应变计算流程如下:给定时间 t时的应力状态和在Δt时间步长内的应变增量,计算在对应时间步长内的应力增量以得到 t+Δt时刻新的应力状态。若在 Δt时间步长内发生了塑性应变,则用 Δt时间内总的应变增量和弹性阶段的本构关系计算得到的应力增量进行修正以得到Δt时间内的真实应力增量。值得注意的是:在本构计算中输入所有的应力都是有效应力,也就是说,在使用本构模型之前,需要将孔隙压力换算成有效应力。
(1)由接触单元弹性阶段的应力 -应变关系和在 Δt时步内的应变增量,计算t+Δt时刻的应力状态σnN。
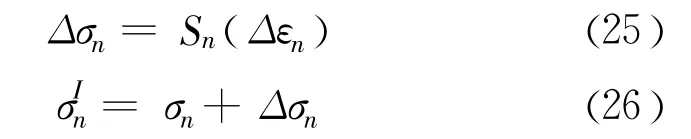
式中:S是弹性应力增量与应变增量之间的关系式,如式(1)是t+Δt时刻的猜想弹性应力。若猜想弹性应力点位于屈服面以下,即没有发生塑性应变,则新应力矢量:

否则,t+Δt时刻的应力状态按下列步骤计算。(2)屈服函数为:

其中 f(σn)表示 f(σx′,σy′,σz′,σx′y′,σy′z′,σx′z′)。在本文所提出的模型中,存在两个屈服函数,即式(7)和(8)中的 fs和ft。
(3)总的应变增量可以分为弹性部分和塑性部分:
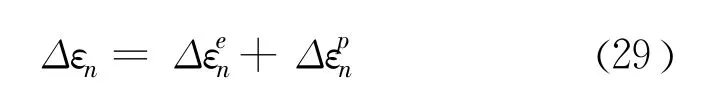
(4)弹性应变增量和应力增量之间满足弹性关系:
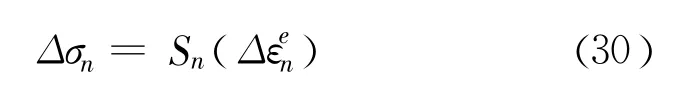
(5)引入塑性流动法则,规定塑性应变增量矢量的方向:

式中:λ是一个常数,具体表达式见式(40);g为塑性势函数,即式(10)和(11)中的 gs和gt。
(6)新的应力状态
在时间 t+Δt时,应力矢量要满足屈服函数 f:

当 f(σn)是σn的线性函数时,上式可以写为:
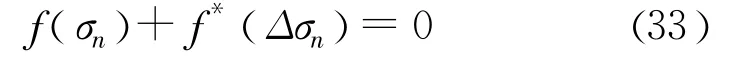
其中,f*作为一种标记,表示函数 f减去此函数的常量部分,即
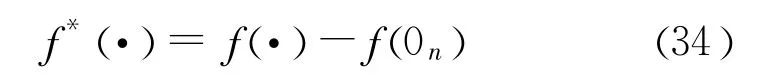
将式(29)代入式(30),并由式(31)得:
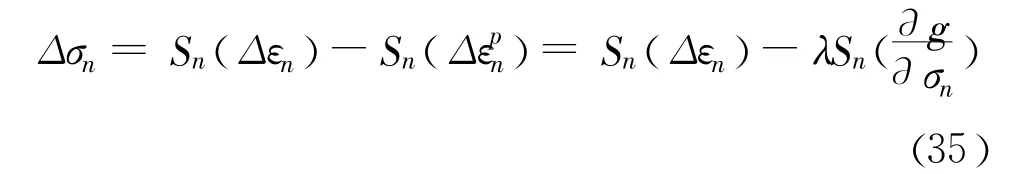
然后
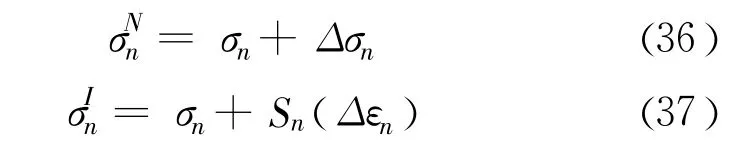
将式(35)代入式(33),并利用式(28),得:
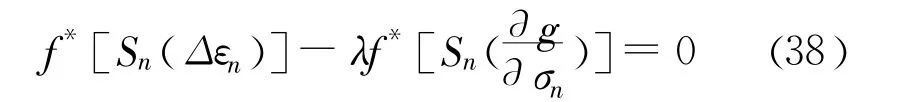
由式(37)且利用函数f的性质得到:
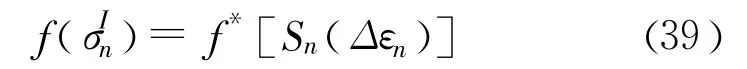
将式(39)代入式(38),并利用式(34),得:
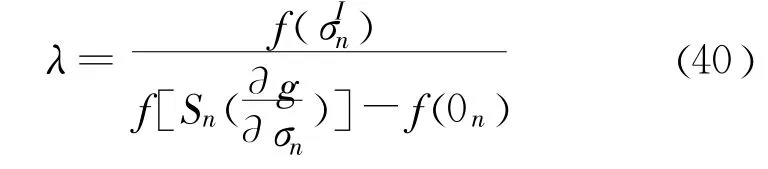
最后,新的应力状态可以从式(35)、式(36)和式(37)推导得:
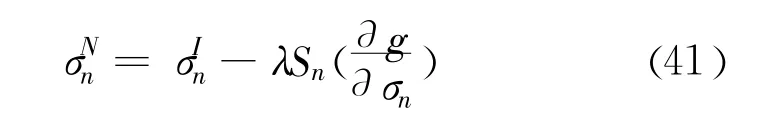
根据以上理论基础,当接触单元发生剪切破坏时:
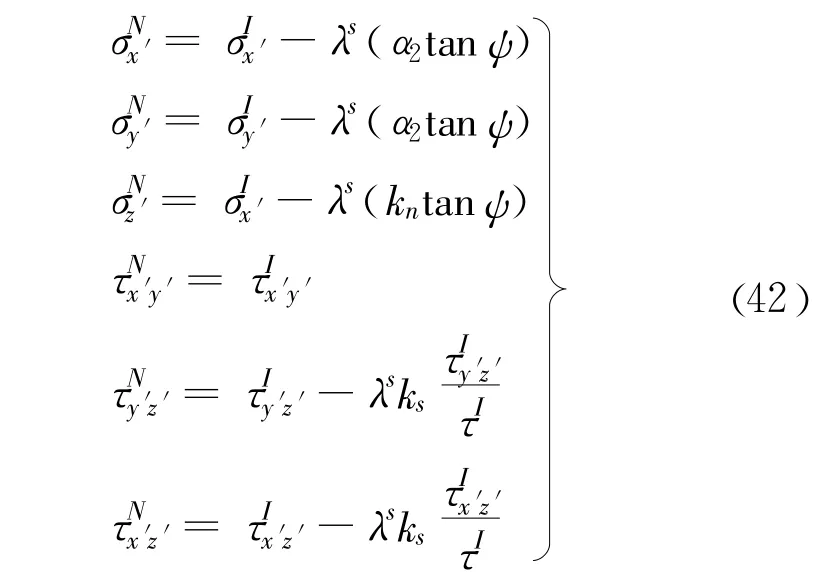
其中
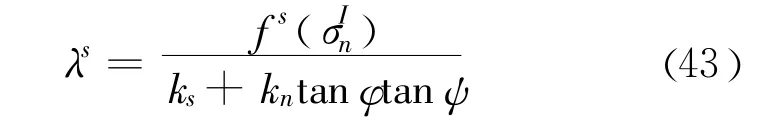
当发生拉伸破坏时:
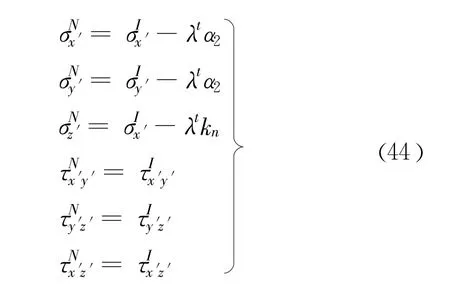
其中

(7)计算接触单元在 t+Δt时刻前所累积的剪切软化参数为:
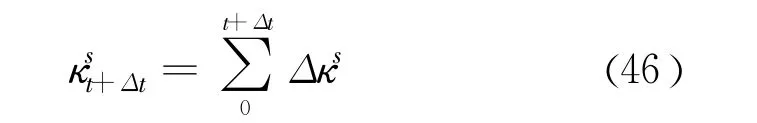
(8)更新强度参数内摩擦角 φ和粘聚力c:
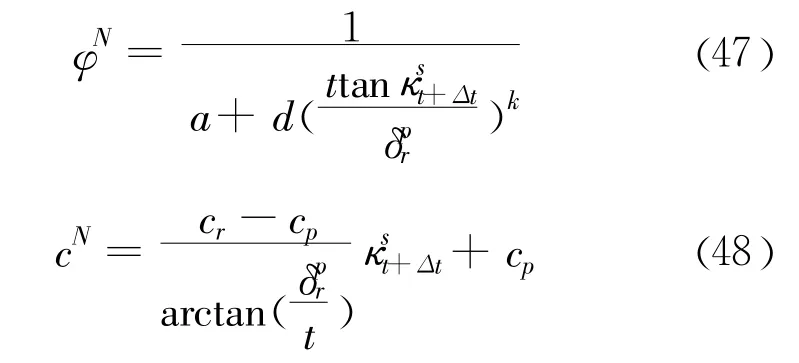
3 单元验证
根据上述思路,利用Visual Studio 2008编写了程序,运行生成动态链接库文件,并在有限差分软件FLAC3D中以命令model完成对新薄层实体接触单元类型的调用。下面用三个算例来验证新单元的正确性。
3.1 单轴压缩试验
图4所示为一个带有弱面的岩石试样。通过证明孔隙压力对含有弱面试样滑移破坏的影响,来验证本文提出的薄层实体接触单元的有效性。
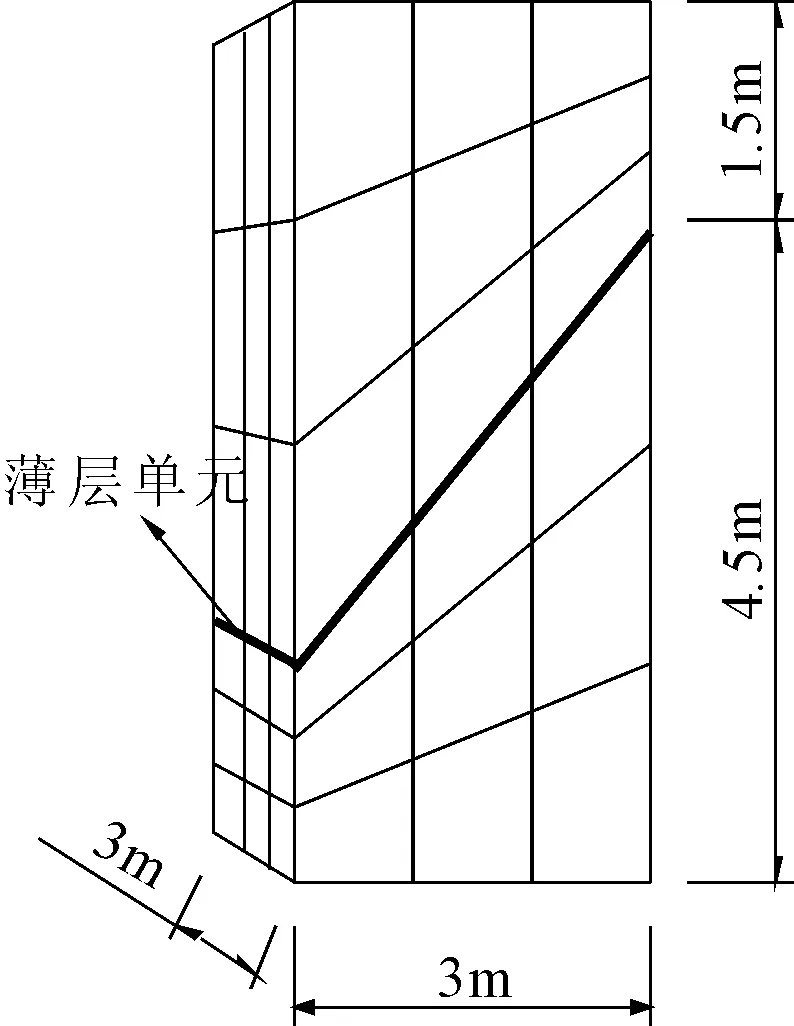
图4 单轴压缩试验模型
设φ是弱面的内摩擦角,β为弱面和垂直方向之间的夹角,当(1-tanφtanβ)>0[18],试样将会沿着弱面滑移。当试样沿着弱面滑移即试样发生破坏时,试样的压力会达到峰值 σ1,而此峰值和弱面的强度参数之间的关系如下式所示[18]:
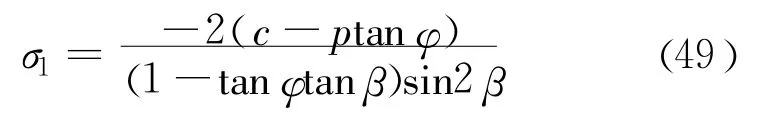
式中,p是试样中的孔隙压力,β取45°。
根据式(49),当无孔隙压力,即 p=0时,σ1=-4.7 kPa;有孔隙压力,p=1.0 kPa时,σ1=-2.0 kPa。对图4所示模型进行两次数值模拟——无孔隙压力和有孔隙压力试验模拟。将两次数值模拟结果分别和理论结果相比。
试验中,在试样的上、下端面同时施加大小为1 ×10-8m/s方向相对的速度,分析中不考虑重力的作用。弱面用本文开发的薄层实体接触单元模拟。接触面的参数根据1.3节由经验值确定。设 G′和K′分别是岩石的剪切模量和体积模量,接触面采用的体积模量 K=1.5K′=150 MPa,剪切模量 G=1.5G′=105MPa,初始切向刚度 ksi=1.5G′=105MPa,初始法向刚度 kni=1.5(K′+4/3G′)=290MPa。试样及薄层接触面的参数如表1和表2所示,其中试样的抗拉强度设置为大值是为了防止试样的受拉屈服。本例不考虑应变软化效应。
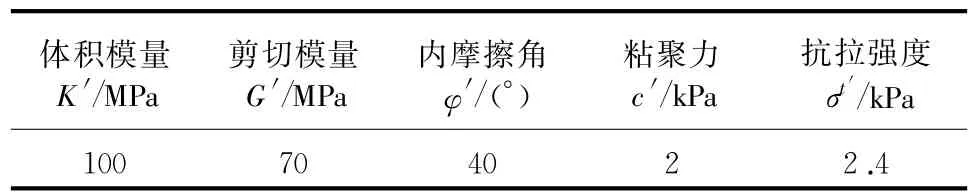
表1 岩石的材料参数
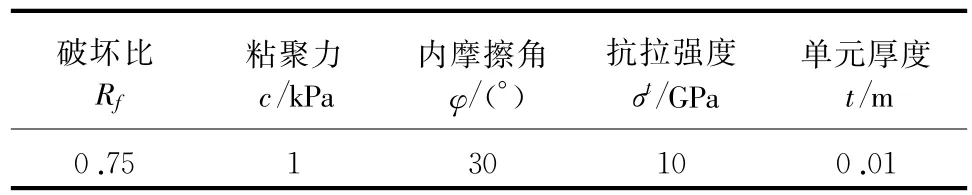
表2 接触面的材料参数
计算得到的不同孔隙压力下试样上端面的轴向压应力和中心轴应变关系如图5所示,并与理论解进行了比较。从图5可以看出,轴向应力计算值虽较理论值有所波动,但基本上趋近于理论值。
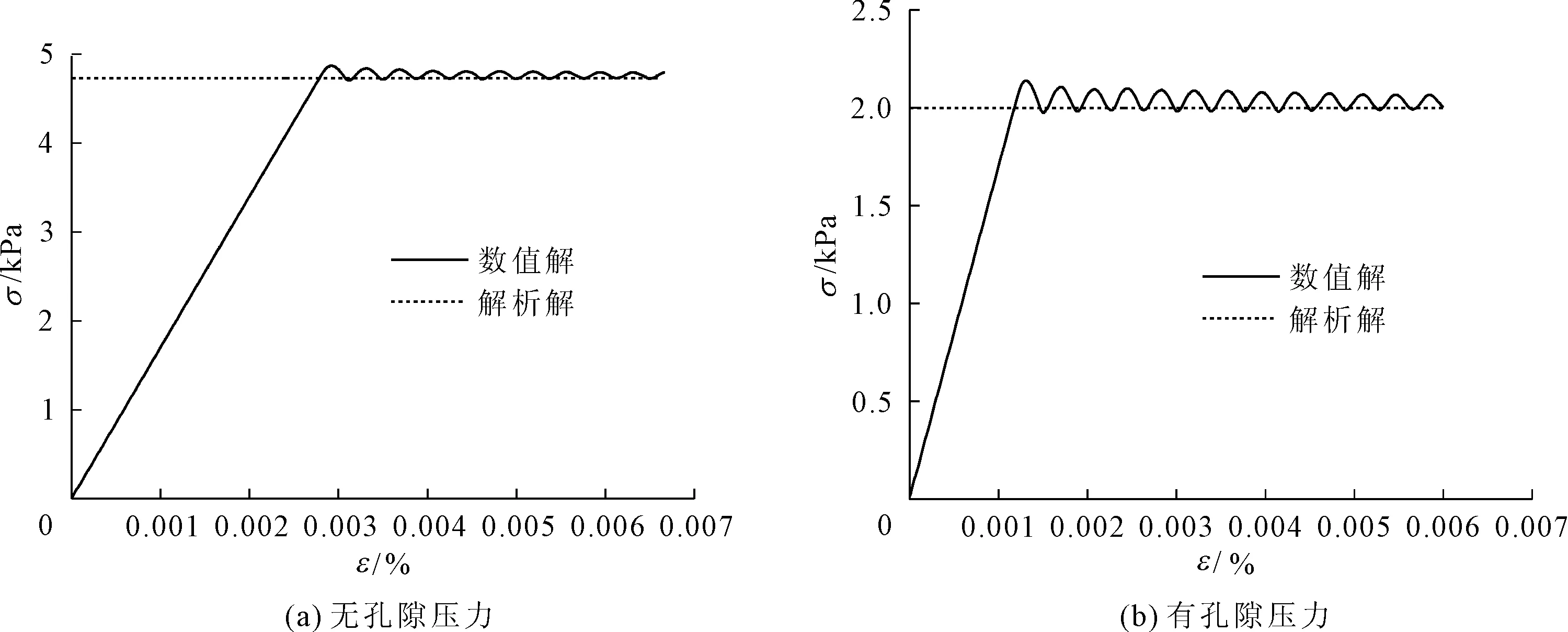
图5 单轴压缩试验模拟结果
3.2 料仓下料模拟
图6为一个料仓下料的实体模型。料仓下料时,料在重力作用下沿着料仓内壁向下滑动,在料仓和料之间存在接触问题。现用本文提出的薄层实体接触单元与FLAC3D软件中内置的interface单元分别对此问题进行模拟。
料仓上端外尺寸为12m×12m,料仓的内尺寸为10m×10m。为了方便观察料的位移变化过程,同时由于模型的对称性,取1/4的整体模型进行模拟,具体尺寸如图6所示。
模型的约束情况:x=0和 x=6m面所有结点受 x向链杆约束;y=0和 y=6 m面所有结点受 y向链杆约束;料仓底部受z向链杆约束。
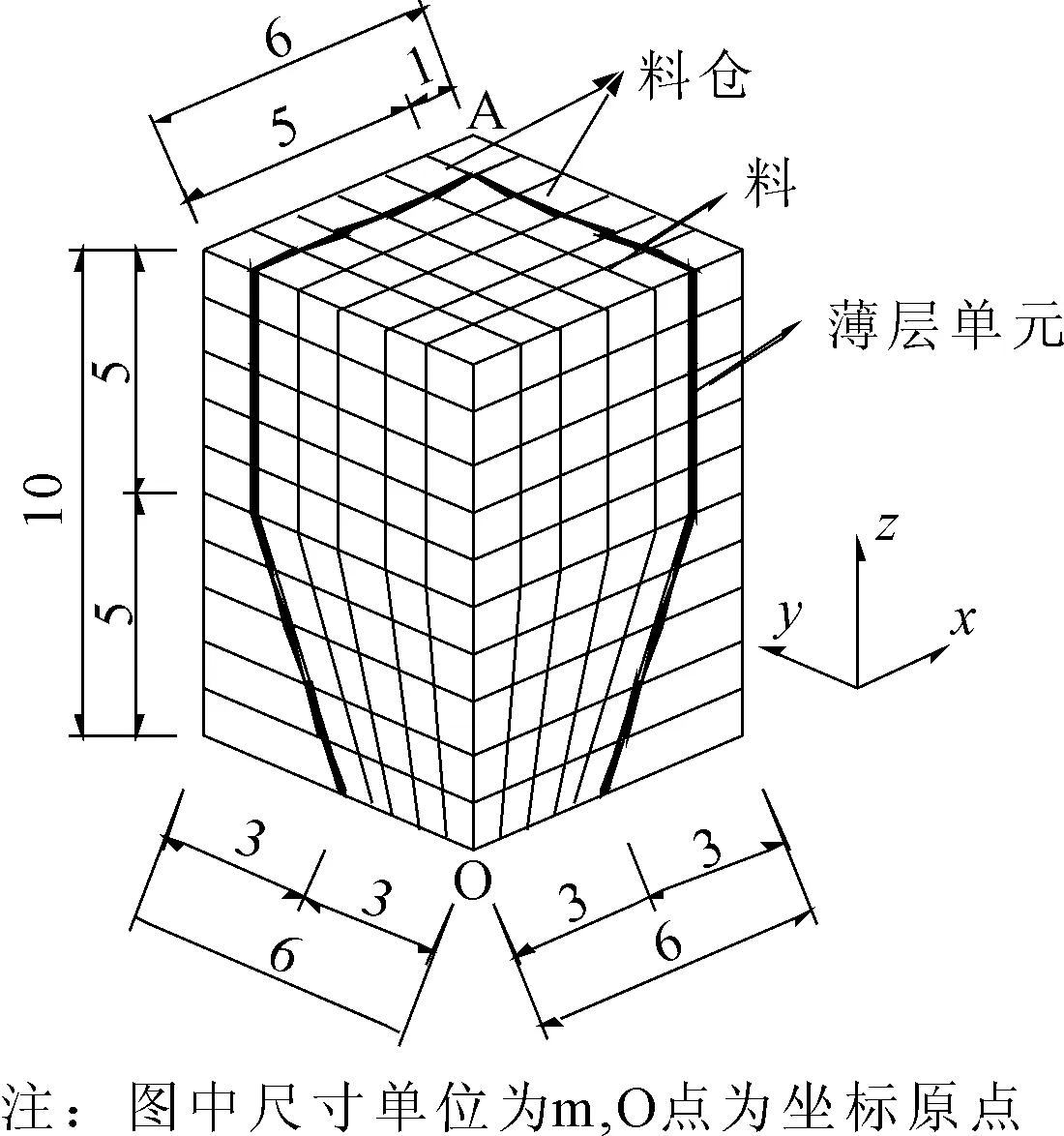
图6 料仓下料模型
按照FLAC3D软件手册[15]的建议,取interface单元的法向刚度 kn=2×109Pa,切向刚度 ks=2× 109Pa。为了和interface单元有更直接的比较,接触面的参数根据1.3节由经验值确定。设 G′和K′分别是料的剪切模量和体积模量,取薄层接触面单元的体积模量 K=K′=200 MPa,剪切模量 G=G′=100MPa,初始切向刚度 ksi=G′=100 MPa,初始法向刚度 kni=(K′+4/3G′)=330 MPa。两种接触的内摩擦角都取为15°。数值计算中所采用的其他材料参数如表3和表4所示。

表3 料仓和料的材料参数

表4 薄层接触面的材料及几何参数
为了验证薄层单元对大变形问题模拟的有效性,数值计算过程中对O、A(如图6)两点的竖向位移进行监测。图7给出了分别采用interface单元和本文薄层实体接触单元进行模拟的对比计算结果,由图7发现采用两种单元所得结果一致性良好。另外,与用interface单元计算相比,用薄层单元计算的A点位移变化过程更平稳更符合实际情况,表明薄层单元能更好地模拟此类问题。
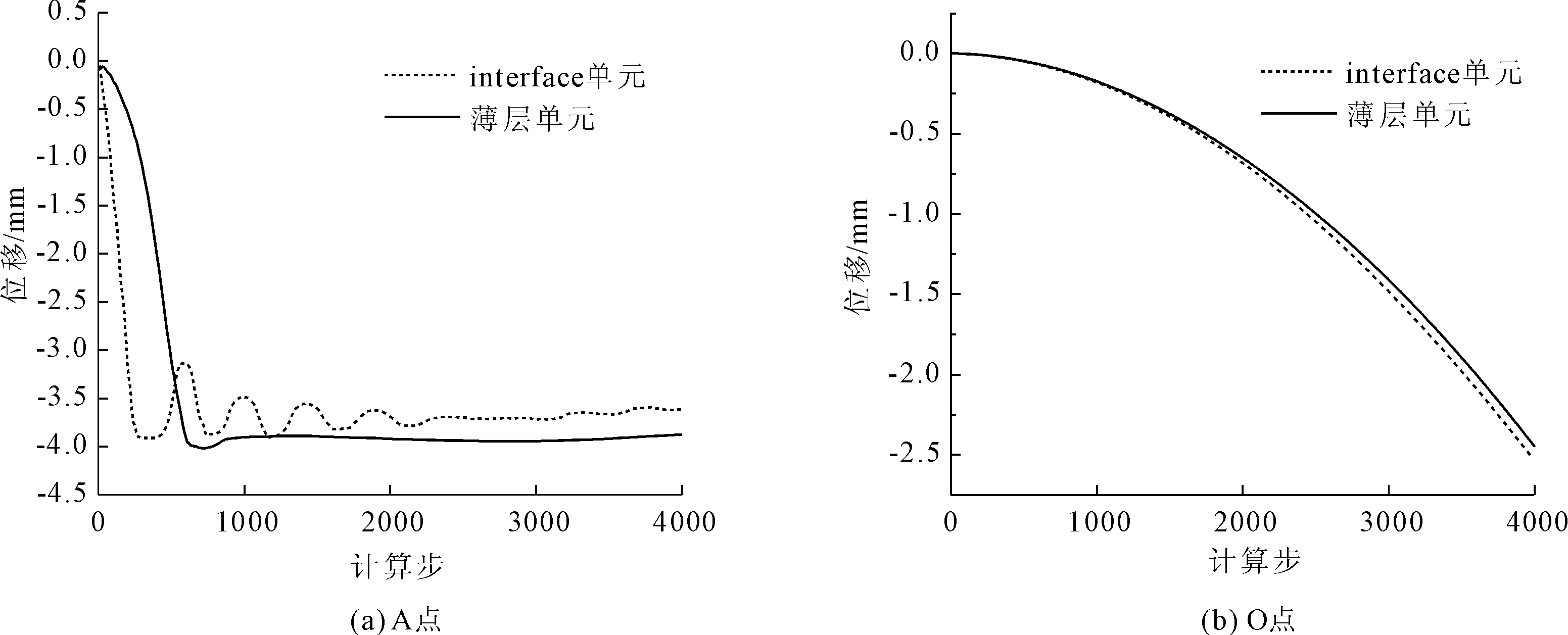
图7 各个监控点的z向位移随计算步的变化曲线
3.3 直剪试验
为了验证本文薄层单元的应变软化和剪胀特性特性,对一个土工膜-土工布之间的直剪试验进行数值模拟,并将数值结果和试验结果[19]相比较。上下剪切盒里盛满砂,上盒的底部固定有一层土工布,而在下盒的顶部固定一层土工膜。由于本试验为模拟试验,所以模型厚度取1m。在试验过程中为了保持剪切面积不变,下盒的顶面面积要大于上盒的底面面积,具体尺寸如图8所示。为了表现接触面的特性,剪切盒内砂的本构采用弹性模型,弹性模量E为50MPa,泊松比ν为0.25。接触面的参数根据1.3节由经验值确定。接触面采用的体积模量 K= 0.96MPa,剪切模量G=1.73MPa,其它的参数取值汇总如表5所示。
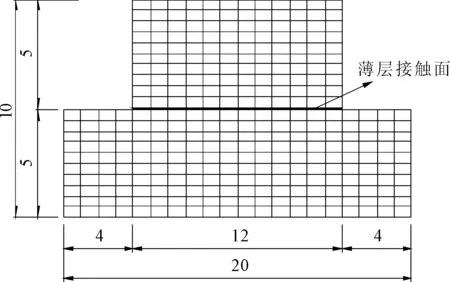
图8 直剪试验模型(单位:m)

表5 直剪试验中薄层接触面采用的参数
试验过程中,下剪切盒固定不动,上剪切盒顶面受到50 kN/m2的均匀压力代表作用在接触面上的侧限压力,然后在上滑块施加向右的大小为5×10-5m/s的速度使上滑块滑动,不考虑重力的作用。滑动过程中,接触面剪切应力τ和切向位移δ关系曲线的数值结果和试验结果比较如图9所示。从图9中可以看出,当切向位移达到5mm时,接触面开始发生屈服,虽然在软化阶段剪切应力数值计算结果比试验结果的变化要快,但两种结果在弹性阶段、峰值剪切应力和残余剪切应力值都非常吻合,表明所开发的薄层单元能很好地预测接触面的软化特性。
同时,为了验证所提出模型能表现接触面的剪胀特性,对本直剪试验在不考虑剪胀特性和考虑剪胀特性(ψ=5°)两种情况进行数值计算,得到接触面法向位移v与切向位移δ之间的关系如图10所示。当接触面开始发生屈服时,考虑剪胀特性的模型法向位移开始增大,也即接触面出现剪胀现象,而不考虑剪胀特性的模型始终没有发生剪胀,可以认为本文所开发的单元能反映接触面的剪胀特性。
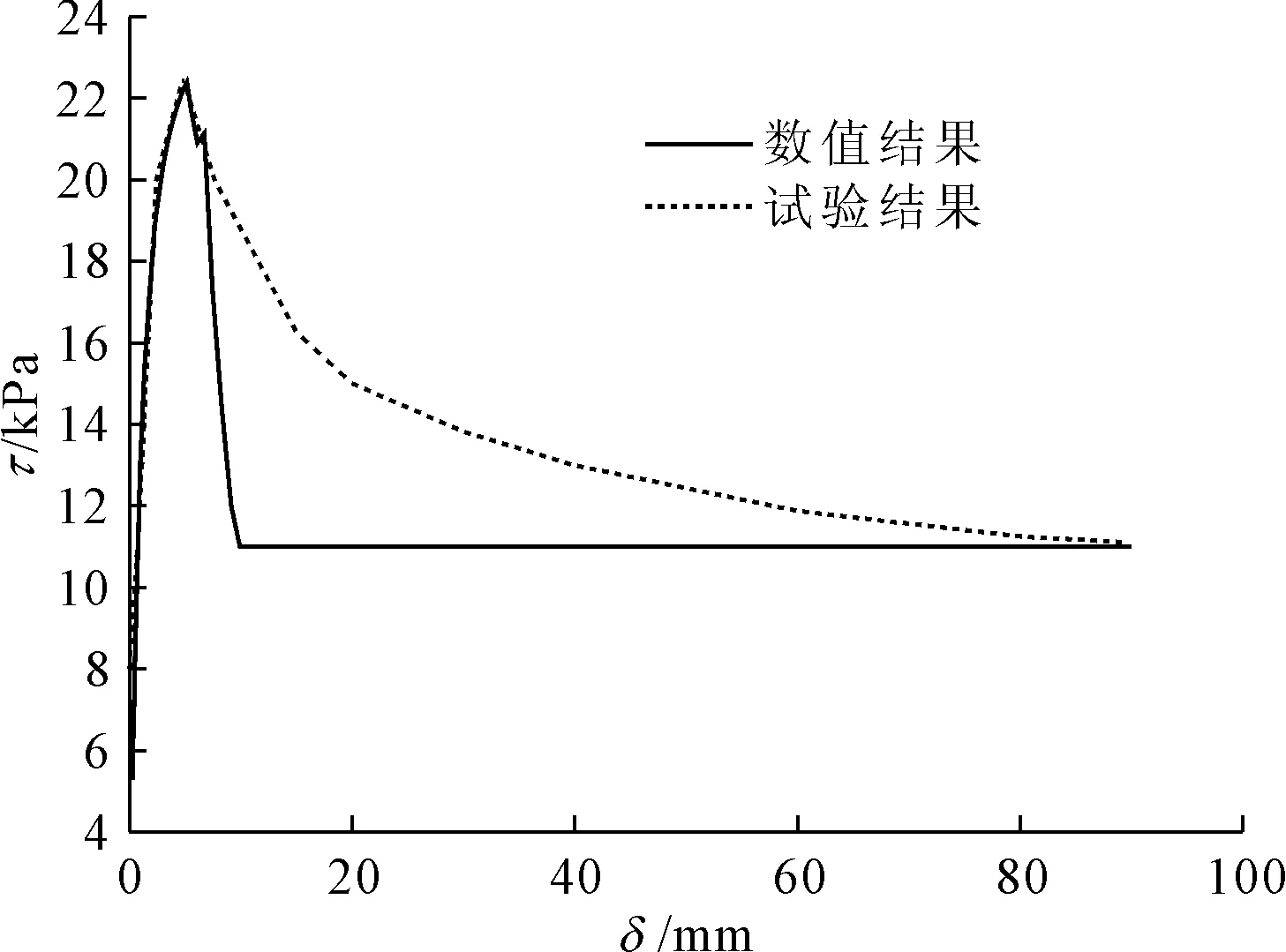
图9 接触面剪切位移 δ 与剪切应力τ曲线数值结果与试验结果的比较
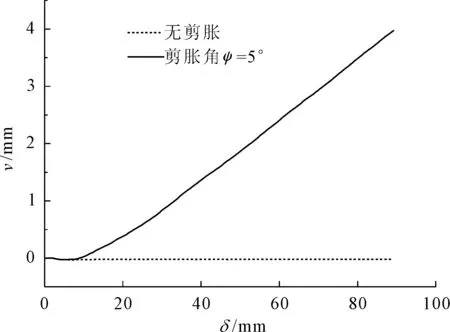
图10 接触面剪切位移δ与法向位移v曲线在不同剪胀特性时的比较
4 结 论
(1)提出了一种弹塑性接触面本构模型,以反映接触面在弹性阶段的非线性,在塑性阶段的基于摩尔-库伦屈服准则的屈服与流动、应变软化、大变形、法向剪胀及拉伸破坏等特性。
(2)将所提出的接触面本构模型表述为适用FLAC3D软件的差分迭代格式,然后基于VC++语言编程,运行生成动态链接库文件,并在此软件中以命令model完成对新薄层实体接触单元类型的调用。
(3)单轴试验的数值解趋近于解析解,证明所开发单元能正确模拟接触面问题,并且对存在孔隙压力的情况依然适用。
(4)料仓下料试验中,用开发的薄层接触单元计算结果和用FLAC3D软件中的interface单元计算结果相比,前者比后者更稳定 ,所以更符合实际情况 ,同时也证明薄层单元对大变形问题模拟的有效性。
(5)直剪试验中,将数值计算结果和试验结果相比较,虽然在软化阶段剪切应力前者比后者变化要快,但两种结果在弹性阶段、峰值剪切应力和残余剪切应力值都非常吻合,证明所开发单元能模拟接触面在弹性阶段的非线性,在塑性阶段的应变软化特性。而考虑接触面剪胀特性的接触面法向位移随切向位移的增大而增大表明所开发的模型能模拟接触面法向剪胀特性。
[1] Zhang G,Zhang J.State of the art:Mechanical behavior of soil-structure interface[J].Progress in Natural Science,2009,19(10):1187-1196.
[2] D’Aguiau SC,Modaressi-Farahmand-Razavi A,Dos Santos JA.Elastoplastic constitutivemodelling of soil–structure interfaces undermonotonic and cyclic loading[J].Computer Geotechnics,2011,38(4):430-447.
[3] Lashkari A.Modeling of sand-structure interfaces under rotation shear[J].Mechanics Research Communications,2010,37(1):32-37.
[4] Peng Kai,Zhu Jungao,Feng Shurong,etal.An elasto-plastic constitutivemodel incorporating strain softening and dilatancy for interface thin-layer element and its verification[J].Journal of Central South University,2012,(19):1988-1998.
[5] Lashkari A.A plasticity model for sand-structure interfaces[J].Journalof Central South University,2012,19(4):1098-1108.
[6] 杜成斌,任青文.用于接触面模拟的三维非线性接触单元[J].东南大学学报:自然科学版,2001,31(4):92-96.
[7] Sharma K G,Desai C S.Analysis and implementation of thin-layer element for interfaces and joints[J].Journalof EngineeringMechancis,1992,118(12):2442-2462.
[8] Wu HM,Shu YM,Zhu JG.Implementation and verification of interface constitutivemodel in FLAC3D[J].Water Science and Engineering,2011,4(3):305-316.
[9] Arab M G,Kavazanjian JE,Fox P J,et al.Displacementsoftening constitutivemodel for geosynthetic interfaces[C]//Proceedings of 14th Pan American Conference on Soil Mechanics and Geotechnical Engineering,Canadian Geotechnical Society on CD Rom,2011.
[10] 陈育民,刘汉龙.邓肯-张本构模型在FLAC3D中的开发与实现[J].岩土力学,2007,28(10):2123-2126.
[11] 左双英,肖 明,陈俊涛.基于Zienkiewicz-Pande屈服准则的弹塑性本构模型在FLAC3D中的二次开发及应用[J].岩土力学,2011,32(11):3515-3520.
[12] 张传庆,周 辉,冯夏庭.统一弹塑性本构模型在FLAC3D中的计算格式[J].岩土力学,2008,29(3):596-602.
[13] Bandis SC,Lumsden A C,Barton N R.Fundamentals of rock jointdeformation[J].International Journalof RockMechanics and Mine Science and Geomechanics Abstract,1983,20(6):249-268.
[14] Clough GW,Duncan JM.Finite element analyses of retainingwall behavior[J].Journalof the SoilMechanics and Foundations Division,1971,97(12):1657-1673.
[15] Itasca Consulting Group,Inc.FLAC3DUserManuals,Version 3.0[M].Minnesota:Itasca Consulting Group,Inc.,2005.
[16] 张冬霁,卢廷浩.一种土与结构接触面模型的建立及其应用[J].岩土工程学报,1998,20(6):62-66.
[17] 栾茂田,武亚军.土与结构间接触面的非线性弹性-理想塑性模型及其应用[J].岩土力学,2004,25(4):507-513.
[18] Jaeger JC,Cook NGW.Fundamentalsof Rock Mechanics[M].Fourth Edition.Malden:Blackwell Publishing,2007.
[19] Jones D R V,Dixon N.Shear strength properties of geomembrane/geotextile interfaces[J].Geotextiles and Geomembranes,1998,16(1):45-71.
Development of A Thin-layer Interface Element and Its Implementation in FLAC3D
LIU Ying-jun,ZHANG Yun-liang
(Faculty of Infrastructure Engineering,Dalian University of Technology,Dalian,Liaoning 116024,China)
With the vigorous developmentof civilengineering and hydraulic engineering,there have beenmore andmore problems about soil-structure interaction.Although there aremany interface constitutivemodels brought up by scholars from home and abroad,most of them are too simple to fulfill the task of simultating interface problems.Interfaces in FLAC3Dare zero-thickness contact elements characterized by Coulomb sliding,which cannot simulate such behaviors as strain-softening.Therefore,based on the theory of plasticity,an elasto-plastic constitutivemodel for soil-structure interaction interfacewas proposed firstly.Then,the constitutivemodelwas implemented by developing a thin-layer solid elementon the software platform FLAC3Dusing VC++language.Finally,three numericalexampleswere presented in detail to confirm the validity of the proposedmodeland the thin-layer element in describing nonlinearbehaviors in the elastic range,strain-softening,large deformation and dilatancy behaviors in the shear direction,aswell as tensile failure in the normal direction during the plastic range.Using the new thin-layer element instead of the original interface element can improve the ability of simulatingmore complicated interface problems of FLAC3D.
interface;thin-layer solid element;elasto-plastic constitutive law;FLAC3D;VC++language
TU45
A
1672—1144(2014)04—0001—08
10.3969/j.issn.1672-1144.2014.04.001
2014-02-24
2014-03-21
国家自然科学基金(50809013);中国水利水电科学研究院开放基金(IWHRO2009019)
刘莹骏(1989—),女 ,河南平顶山人 ,硕士研究生,研究方向为土和结构相互作用。
张运良(1973—),男 ,安徽亳州人 ,博士 ,副教授,主要从事水力发电与核能发电中的水工结构教学与研究。
