低合金钢Q345E静态再结晶模型研究
2014-07-07张秀芝刘建生
李 佳 张秀芝 刘建生
(太原科技大学材料科学与工程学院,山西030024)
低合金钢Q345E静态再结晶模型研究
李 佳 张秀芝 刘建生
(太原科技大学材料科学与工程学院,山西030024)
利用Gleeble-1500D热模拟试验机对低合金高强度结构钢Q345E进行高温双道次热压缩试验,研究不同变形参数下Q345E钢在变形奥氏体区的软化行为,分析各变形参数对该钢静态软化的影响。通过采用0.2%应力补偿法计算得到静态再结晶百分数,确定了Q345E钢的静态再结晶激活能,建立了静态再结晶动力学方程和晶粒尺寸演变模型。
Q345E钢;静态再结晶;动力学方程;晶粒尺寸模型
Q345E是一种低合金高强度结构钢,广泛用于船舶、锅炉、压力容器、风电设备、石油储罐、桥梁、铁路运输、工程机械、车辆及轻化工设备等各类低温环境下使用的工程结构件[1],要求其有很好的力学性能,而材料的力学性能又主要取决于微观组织结构,因此研究材料热加工过程中的微观组织结构可以有效地优化材料加工工艺参数。
在高温热成形过程中,金属材料内部会同时发生加工硬化和回复、再结晶软化两个过程。再结晶方式存在动态再结晶、亚动态再结晶和静态再结晶,而静态再结晶也是加工过程中的一个重要的软化方式。在变形量小于动态再结晶临界应变量的情况下,材料会发生静态再结晶,以优化工件内部的微观组织状态[2~3]。因此,研究材料在成形过程中的再结晶的规律对于控制热加工时的组织与性能具有重要意义。
本文主要研究Q345E钢在锻态条件下奥氏体区的静态再结晶软化行为,确定Q345E钢的静态再结晶的激活能,并通过实验数据建立了静态再结晶动力学方程和晶粒尺寸模型,为制定合理的热加工工艺提供了试验和理论依据。
1 试验材料及方法
本试验所用材料取自Q345E钢锻坯,试样为∅8 mm×12 mm圆柱形试样,材料的主要化学成分见表1。实验在Gleeble-1500D热模拟试验机上进行,采用双道次压缩试验,测试真应力-真应变曲线。试验时将试样以10℃/s的速度加热到1 200℃,保温180 s后以5℃/s的冷却速度降低到各形变温度(分别为950℃、1 000℃、1 050℃、1 100℃),保温60 s以保证试样内部温度的均匀,然后进行双道次压缩变形,变形过程中温度保持恒温。应变速率分别为0.01s-1、0.1s-1、0.5s-1、1s-1,两道次的变形量均为20%。压缩过程在真空气氛下,试样两端加放钽片,以减少摩擦对应力状态的影响。双道次压缩热模拟工艺如图1所示。

表1 试样主要的化学成分(质量分数,%)Table 1 M ain chem ical compositions of the samp le (mass fraction,%)

图1 双道次压缩试验过程示意图Figure 1 Diagram of double-pass hot compression test process

图2 静态再结晶双道次压缩试验应力-应变曲线Figure 2 The diagram of static recrystallization stress-strain in double-pass compression experiment
2 试验结果与分析
2.1 应力-应变曲线
图2为实验测定的应力-应变曲线。由图2 (a)可知,在相等的间隔时间内,变形温度越高,材料的流变应力越低,这说明静态再结晶软化百分数随温度升高而增加。由图2(b)可知,在相同变形条件下,随着道次间隔时间的增加,流变应力相应有所降低。在间隔时间为5 s时降幅较大,大于5 s时流变应力变化很小,这说明在1 000℃和间隔时间5 s内材料发生了比较充分的静态再结晶软化。
2.2 静态再结晶百分数
静态再结晶的研究方法一般是采用双道次压缩试验,主要是通过两道次的应力-应变曲线计算获得的静态再结晶软化率来判断材料的静态再结晶软化行为。软化率的计算方法主要有:屈服应力的0.2%补偿法、2%补偿法,总应力的5%补偿法、后插法、平均应力法及面积法等方法[4~8]。由于0.2%补偿法所得到的数据误差比其他几种方法小,因此本文采用屈服应力的0.2%补偿法处理。0.2%补偿法的软化率Fs由下式测定:
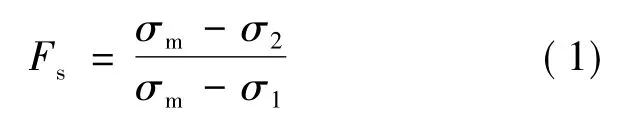
式中,σm为第一次加载结束时的应力;σ1、σ2分别为第一次、第二次加载时的屈服应力。由于静态软化包括静态回复和静态再结晶,所以通常定义静态再结晶在Fs=0.2时开始[9]。静态再结晶体积百分数为:

2.3 静态再结晶动力学
对于钢中奥氏体静态再结晶动力学模型的研究,一般采用方程来描述:

式中,n为常数;t0.5为静态再结晶率达到50%的时间;C=-0.693。对式(3)两边取自然对数,得到:

XSrex-ln t关系见图3。

图3 XSrex-ln t关系Figure 3 The relationship between XSrexand ln t
对于某种具体的材料或者变形参数,t0.5和n是定值,因此对实验数据分别进行线性回归,做出ln( l n() )-ln t的关系图(图4),可得到n的平均值:=0.335。
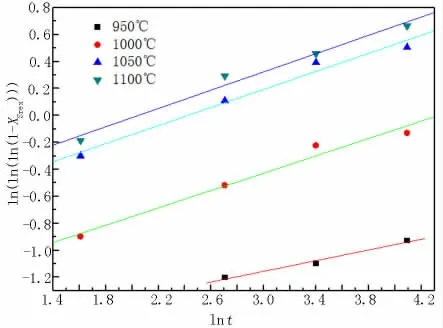
图4 ln( l n())-ln t的关系Figure 4 The relationship between ln( l n() )and ln t

图5 ln t0.5-1000/T关系Figure 5 The relationship between ln t0.5and 1000/T
2.4 静态再结晶激活能QSrex的确定
静态再结晶量达到50%所用时间可以用以下公式描述:
当ε<εc时,

其中,A、a1、a2、a3为材料常数;ε为真应变;ε·为应变速率(s-1),R为气体常数(J/mol·K);T为绝对温度(K);QSrex为静态再结晶激活能(J/ mol);d0为材料的初始晶粒尺寸(μm)。
对式(5)两边取自然对数,得到:

由式(6)可知,ln t0.5与1000/T呈线性关系。利用最小二乘法对实验数据进行回归,可以得到ln t0.5与1/T之间的关系,如图5所示。得出静态再结晶激活能QSrex=185.330kJ/mol。
2.5 静态再结晶晶粒尺寸模型[10~11]
静态再结晶过程中,由于道次间间隔时间对静态再结晶的影响较小,因此静态再结晶晶粒尺寸模型可由下式描述:

对式(7)两边取自然对数,得到:

根据实验数据对各个系数进行线性回归,得到:
A1=327.72,a4=0.489 2,a5=-0.664 6,a6=-0.076 1,Q=-59 701.14 J/mol。
得到的静态再结晶晶粒尺寸模型为:

3 结论
(1)在同等的间隔时间内,材料的变形温度越高,其流变应力越低,即静态再结晶软化百分数随温度升高而增加。在相同变形条件下,随着道次间隔时间的增加,流变应力相应有所降低,间隔时间15 s内材料发生了比较充分的静态再结晶软化。
(2)根据实验结果,得到了Q345E钢的静态再结晶激活能,建立了静态再结晶的动力学方程和静态再结晶晶粒尺寸模型。
[1] 张毅峰,王雷刚,吴君三,胡振奇.大直径风塔法兰异型环锻件双件合轧工艺模拟与试验[J].金属铸锻焊技术,2010,39(19):89-93.
[2] 沈丙振,方能炜,沈厚发,等.低碳钢奥氏体再结晶模型的建立[J].材料科学与工艺,2005,13(5):516-520.
[3] 蔺永诚,陈明松,钟掘.42CrMo钢形变奥氏体的静态再结晶[J].中南大学学报,2009,40(2):411-416.
[4] Devadas C,Samarasekera I,Hawbolt E B.The Thermal and Metallurgical State of Steel St rip During Hot Rolling[J]:PartⅢ.Microst ructural Evolution.Metall Trans A,1991,22: 355.
[5] Medina SF,Mancilla JE.Static Recrystallization Modeling of Hot Deformed Steel Containing Several Alloying Elements[J]. ISIJInt,1996,36(8):1070.
[6] 陈俊,周砚磊,唐帅,刘振宇,王国栋.Nb-Ti微合金钢的静态再结晶行为[J].钢铁,2012,47(5):54-58.
[7] 李立新,洪杰,邓宁,等.含硼微合金钢静态及亚动态再结晶动力学模型研究[J].武汉科技大学学报:自然科学版,2004,27(4):334-336.
[8] 刘振宇,许云波,王国栋.热轧钢材组织-性能演变的模拟和预测[M].沈阳:东北大学出版社,2004.
[9] SUNW P,Hawbolt E B.Comparison between static andmetadynamic recrystallization an application to the hot rolling of steels[J].ISIJ International,1997,37(10):1000-1009.
[10] 李壮,张平礼,周晓光,吴迪,刘建勋,徐佩笔.热轧钢板奥氏体再结晶晶粒尺寸的预测模型[J].机械工料,2005,29 (9):16-17.
[11] 窦晓峰,鹿守礼,赵辉.Q235低碳钢静态再结晶模型的建立[J].北京科技大学学报,1999,21(1):20-22.
编辑 杜青泉
Static Recrystallization Models of Low-alloy Q345E Steel
Li jia,Zhang Xiuzhi,Liu Jiansheng
High-temperature double-pass compression was conducted on Q345E high strength low alloy(HSLA) steel by using Gleeble-1500D thermal stimulator,in order to analyze the softening behaviour of deformed austenite of Q345E steel under different parameters and the influence of these parameters on the static softening process.By adopting 0.2%stress compensationmethod,the recrystallized percentage was defined,the static recrystallization activation energy of Q345E was also determined,the kineticsmodel of static recrystallization aswell as themodel of grain size evolution were established.
Q345E steel;static recrystallization;kineticsmodel;grain sizemodel
TG111.7
A
2013—04—07
太原市科技项目(编号:120224)。
李佳(1986—),男,硕士研究生,主要研究方向是大型锻造理论与新技术。刘建生,男,教授,博士生导师。
