基于滞回碰摩力模型的转子系统碰摩响应研究

曹登庆，杨 洋，王德友，陈华涛，姜广义

（1.哈尔滨工业大学航天学院，哈尔滨150001；2.中航工业沈阳发动机设计研究所，沈阳110015）

基于滞回碰摩力模型的转子系统碰摩响应研究

曹登庆1，杨 洋1，王德友2，陈华涛1，姜广义2

（1.哈尔滨工业大学航天学院，哈尔滨150001；2.中航工业沈阳发动机设计研究所，沈阳110015）

转/静子碰摩是影响旋转机械的稳定性与安全性的重要因素之一，而碰摩力的表征则是预测转子系统动力学响应的关键问题。讨论了已有转/静子碰摩力模型的适用范围，重点阐述滞回碰摩力模型的物理意义，并与几种经典的碰摩力模型进行比较；以Jeffcott转子作为典型例子，基于滞回碰摩力模型给出系统的碰摩响应，并与采用线性碰摩力模型所得到的碰摩响应进行比较；利用数值仿真的结果分析静子刚度、转子偏心距等因素对采用滞回碰摩力模型的转子碰摩响应的影响。数值仿真的结果表明：采用滞回碰摩力模型得出的失稳速度(1226 rad/s)低于采用线性碰摩力模型得出的失稳速度(1476 rad/s)，且系统的动力学特性更为复杂，因此，可以更真实地反应碰摩的物理实质。

Jeffcott转子；碰摩；线性模型；赫兹模型；滞回模型

0 引言

旋转机械转/静子碰摩是由于转子的变形量与其振动位移相加大于预留的动静件间隙而引发的次生故障[1]，对旋转机械的设计和安全运行至关重要，国内外学者为此进行了广泛研究。

转/静子碰摩可分为刚性碰摩和弹性碰摩2种。刚性碰摩是指在转/静子发生碰摩时，只会相互接触但不会发生嵌入变形，同时所激发出的切向库伦摩擦力会导致转子发生摩擦失稳现象，分为全周碰摩和局部碰摩。与刚性碰摩相比，弹性碰摩故障的发生更为普遍，其研究模型通常分为：瞬时冲击碰撞力模型和连续接触碰撞力模型2种。瞬时冲击碰撞力模型是指在碰撞过程中仅考虑碰撞前后的能量交换，碰撞前与碰撞后速度的瞬时跳跃通过动量守恒定律和恢复系数来判定[2-3]。该模型的计算效率较高，因此在大型多刚体系统碰撞动力学仿真中得到了广泛应用[4-6]，但其用于转子碰摩时存在明显的缺陷，不能有效地反映转/静子的结构特性对碰摩过程的影响，而且忽略了碰撞过程，仅考虑碰撞前后的瞬时也会给系统响应计算带来较大误差。

连续接触碰摩力模型可以描述弹性体在接触过程中的挤压和弹开过程，需要通过接触物之间的嵌入速度和嵌入位移来确定，因此更能反映不同转/静子碰摩过程的差异，包括碰撞刚度，切入速度、切入角度和材料常数等。该模型可分为线性模型和非线性模型。线性弹簧阻尼接触力模型以Kelvin-Voigt模型[7-8]为代表，由线性弹簧和阻尼器并联而成，在分析接触碰撞问题时比较简便，但无法计算碰撞开始时的不连续问题。1881年，Hertz提出了1种非线性接触力模型[9-10]，在此基础上，国内外学者相继建立了一系列非线性接触力模型；Hunt[11]和Herbert[12]等认为含间隙运动副中接触碰撞力应与相对位移的n次方成正比；此外，部分学者将2种接触碰摩力模型相结合，如Dubowsky等[13-14]，基于Hertz的理论；有关连接结构接触碰撞的接触力模型的评述可参见曹登庆等的综述[15]。

虽然转/静子结构及研究的侧重点不同，但线性碰摩力模型和非线性碰摩力模型均被广泛应用。如陈果[16-17]建立的航空发动机整机动力学模型，其碰撞力用线性弹簧模型描述，摩擦力采用库伦摩擦力；杨树华[18]基于Hertz接触理论的研究——转子非线性碰摩模型，通过计算指出，相比于线性碰摩力模型，非线性碰摩模型能更深刻地反映出转/静子碰摩过程的本质特征，但缺乏相应的试验数据支撑。

在对转/静子进行动力学建模时，正如文献[1]所述：一方面应建立充分考虑碰摩局部动/静件材料特性和相互作用力学特征的局部碰摩模型，其中包含准确给出各种碰摩力的正确形式以及选择或识别符合实际的物理参数等；另一方面，要建立充分考虑转子和静子主要动力学特征的碰摩模型，其中包含合理的计算及转子和定子参与响应的主要模态，能够正确反映系统局部点的碰摩对系统整体动力学特性影响的特征；此外，还要考虑在碰摩过程中具有实质影响的、典型的周围接触介质的变化（油膜力和气尖力等），以及由摩擦和热效应造成的结构形式的变化和带负荷转子受到气流的附加扭矩及其变化等。

为了方便阐述转/静子碰摩问题，本文仅以单盘Jeffcott转子为例，分别采用哈尔滨工业大学曹登庆课题组近期提出的反映碰摩力滞回特性的碰摩模型[19]和最为常用的线性碰摩模型对转/静子碰摩的动力学响应特征进行对比分析。

1 转/静子碰摩力模型

转/静子碰摩成为转子动力学的难题原因是在于当转子与静子发生碰摩时，系统是1种非光滑的、高维强非线性系统，并且包含了相互影响的众多控制参数[20-23]。解决这类复杂的动力学问题的前提是如何建立非光滑系统的动力学模型。下面主要介绍几种经典的转/静子碰摩力模型，分析其适用范围，并重点阐述滞回碰摩力模型的物理意义，并与几种经典碰摩力模型进行比较。

1.1 瞬时冲击模型

基于经典的碰撞定律[24]，碰撞前、后的恢复系数可以写成

式中ν-、ν+分别为碰撞前、后的切向速度；为恢复系数。

转/静子碰摩开始与结束瞬时的法向和切向速度之间的关系为

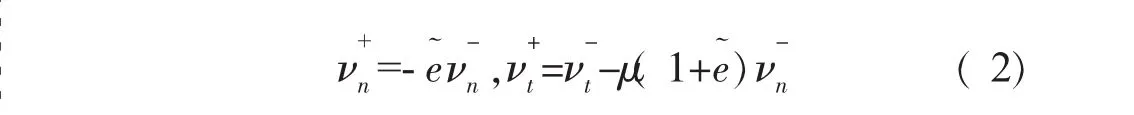
当碰撞速度较大时，其碰撞过程十分短暂，因此忽略碰撞过程是合理的。在此情况下，利用该模型进行分析，具有计算效率高的优点。但是利用该模型进行转/静子碰摩分析，存在以下不足：

（1）该模型不能有效反映转/静子的结构特征对碰摩的影响；

（2）仅考虑碰撞前、后的瞬时，即忽略碰撞过程，这会给系统响应求解带来较大误差；

（3）不能反映碰撞过程中结构的阻尼效应。

1.2 连续接触碰撞力模型

1.2.1 线性碰摩力模型

1.2.1.1 无阻尼碰撞力模型

线性无阻尼碰撞力模型是将转子与静子的碰撞过程用线性弹簧描述，并将弹簧刚度定义为碰撞刚度，同时摩擦模型采用库伦摩擦，如图1所示。当转盘的径向位移r大于转/静子间隙r0时，转子与静子发生碰撞并产生摩擦，相应的碰撞正压力和库伦摩擦力可表示为

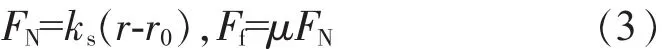
图1 线性碰撞正压力模型

式中：k为转轴刚度；ks为静子刚度即碰撞刚度；μ为库伦摩擦系数。

1.2.1.2 线性阻尼碰撞力模型

Hunt和Crossley[11]于1975年提出了同时考虑线性弹性力和线性阻尼力的碰撞力模型，即

式中：常数c为接触碰撞的法向黏性阻尼系数。

线性碰摩力模型是1个分段线性的非线性模型，以静子的结构刚度作为碰撞刚度，这实质上是采用了准静态假设，用静态刚度近似地表示碰撞刚度。采用线性碰摩力模型需满足以下条件：

（1）静子结构刚度相对较小；

（2）碰撞速度相对较低，即满足准静态条件；

（3）碰撞嵌入位移相对较小，即结构变形仍然在线性范围内，忽略几何非线性的影响。

根据条件（1），由于机匣的结构刚度仅为转子刚度的若干倍，该模型可用于航空发动机转/静子碰摩，而对于结构刚度很大的汽轮机静子（接近刚性）则不适用。由于该模型采用准静态假设，与碰撞速度无关，所以无法计及碰撞动刚度的影响。

1.2.2 非线性碰摩力模型

1.2.2.1 Hertz碰摩力模型

Hertz碰摩力模型是基于Hertz接触理论建立的非线性碰摩力模型，其碰撞正压力曲线如图2所示。使用该碰摩力模型时需要做如下假设：

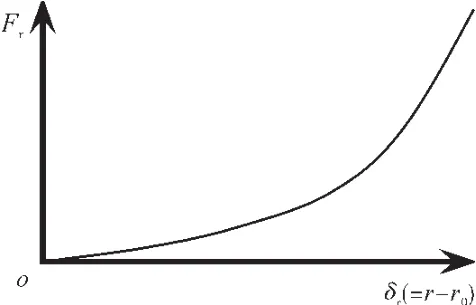
图2 Hertz碰摩正压力模型

（1）理论上将2弹性体在曲面处的接触视为点接触，接触压力垂直于二者的公切面；

（2）将接触表面视为理想的光滑表面，不考虑摩擦效应；

（3）转/静子碰摩过程中仅在挤压接触区域有局部弹性变形，静子结构不会变形；

（4）在碰撞过程中的摩擦力按库伦摩擦定律计算。

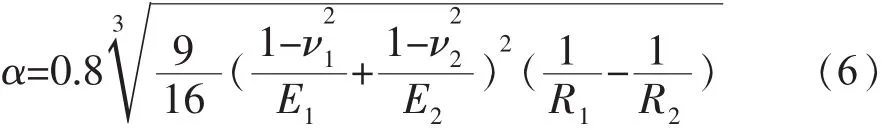
式中：δr为径向嵌入深度；ν1、E1、R1分别为转子的泊松比、杨氏模量和撞击局部表面的曲率半径；ν2、E2、R2则分别表示静子的泊松比、杨氏模量和撞击局部表面的曲率半径。

Hertz碰摩力模型由2个碰撞体的材料常数以及撞击局部表面的曲率半径来确定。因为机匣刚度仅为转子刚度的若干倍，碰撞力会使机匣产生弹性变形，根据条件（3），该模型可用于结构刚度很大的汽轮机静子，而对于航空发动机机匣则不适用。

1.2.2.2 L-N碰摩力模型

基于Hertz接触理论，Hunt和Crossley[11]提出了非线性弹簧阻尼模型。在接触碰撞初始时，Hunt-Crossley模型的碰撞力是连续的，并且考虑了接触过程中的能量损失，其碰撞力与变形的非线性关系为

式中：k为接触碰撞刚度；η为接触阻尼因子，与恢复系数有关；n为变形量指数，根据几何形状的差异，可选取不同的值。

在Hunt-Crossley模型的基础上，Lankarani等[25]提出了通过碰撞前、后的能量损失来确定阻尼因子的具体方法，建立了Lankarani-Nikra-vesh（L-N）碰摩力模型。

假设碰撞物体的质量为m，碰撞时的初始速度为

式中：常数α由转/静子的材料常数及结构几何参数来确定，即

因此转/静子法向碰撞力可表示为ν0，碰撞恢复系数为，则碰撞前、后动能损失ΔT为

物体因碰撞发生嵌入时，系统的能量损失应等于接触力滞回环内所作的功，即

根据式（8）、（9）可以求得接触阻尼因子

与线性模型和Hertz模型相比，L-N模型全面反映了碰撞物体的材料属性、局部变形、碰撞速度等信息，且能够反映接触碰撞过程中的能量损失行为。但该模型也存在一定的不足，即只适用于恢复系数较大的情况，无法反映恢复系数较小时的情况。

无论是线性碰摩力模型，还是Hertz碰摩力模型或是在Hertz理论基础上改进的碰摩力模型，共同特点是采用了准静态假设，无法描述在碰撞过程中碰撞力随时间变化的规律。虽然L-N模型计及了碰撞前物体速度的影响，但仍然无法描述碰撞瞬时动刚度的影响。

1.3 滞回碰摩力模型

根据文献[19]采用摆式碰撞装置得到的相关试验数据，可以拟合出如图3所示的“滞回”型碰摩力曲线。根据试验分析，碰摩问题应具有如下特点：

（1）碰撞正压力应与结构弹性变形相关，因此应包含与结构刚度相关的信息；

（2）碰撞后嵌入量的大小应与碰撞前接触面法线方向的速度相关；

（3）碰撞问题涉及到瞬态冲击，在发生碰撞的初始段其冲量较大，随着位移的增大，其动态正压力部分会迅速降低；

（4）碰撞正压力应与接触阻尼相关，即与速度相关，且应是某种非线性关系；

（5）接触阻尼系数应与速度指数及与2个碰撞物体的材料相关。

根据上述特点，将碰摩试验所得数据进行拟合，文献[19]提出采用下述表达式来表征碰撞力

图3 “滞回”碰摩力模型

式中：H（δ）是Heaveside函数；ks为静子的结构刚度（静刚度）；kd为碰撞初段的动刚度，通常取静刚度的5～8倍；C、α分别为阻尼系数和速度指数，取值均应大于零，与实际转/静子系统的结构参数有关，可由试验数据拟合得到；δmax为碰撞发生后的最大嵌入量，在计算转/静子碰撞后的最大嵌入量时，不计碰撞过程中的能量损失，利用能量守恒原理，最大嵌入量可以表示为

式中：v0为碰撞前瞬时转子的径向速度。

碰撞时的摩擦力仍采用库伦定律，即

由于碰撞力具有滞回特性，用式（11）和式（13）表征的碰摩力称为滞回碰摩力模型，可用于研究航空发动机转子与机匣间发生的转/静子碰摩。

2 转/静子碰摩响应分析

现代航空发动机通过减小转静子间隙来追求高推重比，因此转子叶片与静子机匣间碰摩故障的发生率大幅增加。由于机匣壁较薄，当转子与机匣发生碰摩时，会造成机匣发生明显的弹性变形而不再是局部变形，加之接触表面是非光滑的，基于以上考虑，使用Hertz碰摩力模型是不合适的。这里采用滞回碰摩力模型进行碰摩响应计算，并将计算结果与采用线性碰摩力模型得到的响应进行对比分析。

为了便于阐述问题，以单盘的Jeffcott转子为例，考虑稳态运行（在恒定转速下）的碰摩为主，相应的转/静子系统运动方程为

式中：m、c、k分别为转子的质量、阻尼和刚度；e为转子偏心；x、y分别为横向和竖向振动；Fxf、Fyf分别为碰摩力在横向和竖向的投影。

对Jeffcott转子进行动力学分析时采用的参数见表1。

2.1 2种碰摩力对转/静子系统响应的影响

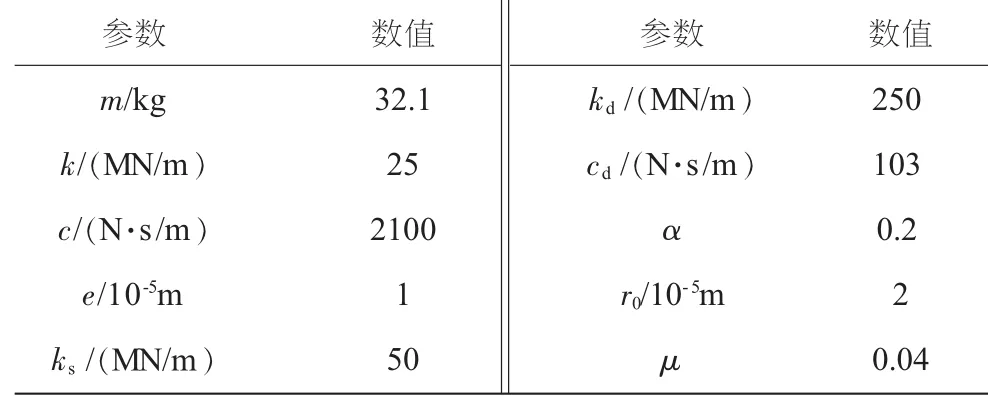
表1 转子主要计算参数

为了分析线性碰摩力模型和滞回碰摩力模型对转/静子系统振动特性造成的差异，将转速取为系统的分岔参数，针对每一给定的转速，采用4阶Runge-Kutta法进行数值积分，绘制出转子的响应分岔图。常用的数值算法在一定程度上无法真实模拟碰撞过程，因此本文利用线性插值法分析系统碰摩过程中出现的跨越现象，在碰撞界面上采用线性差值法修正积分步长，以提高计算结果的精确度。

2.1.1 线性碰摩力模型

采用线性碰摩力模型时，得到的转子系统响应分岔图如图4所示，其中横轴是转速ω，纵轴是转子的横向振动x。当转速较慢时，系统作周期1运动；随着转速的加快，在一定速度范围内，分岔图中出现了大量密集的点，此时系统作拟周期运动；当转速继续加快时，系统再次恢复到周期1运动。

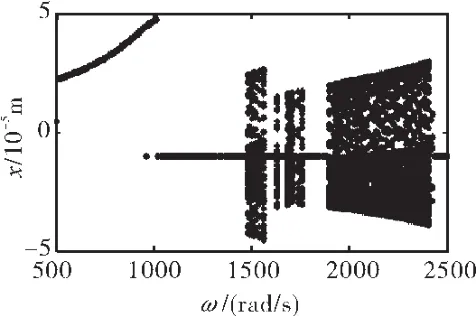
图4 转子响应分岔图（线性碰摩力模型）

图5 转子系统响应（线性碰摩力模型，ω=1800 rad/s）

图6 转子系统响应（线性碰摩力模型，ω=2500 rad/s）

为了进一步分析不同转速下系统的响应，选取ω=1800、2500 rad/s绘制时间历程曲线图、轴心轨迹图、相图和Poincare映射图，分别如图5、6所示。

从图5、6可见，在这2个转速下，系统的时间历程曲线是规则的周期运动，轴心轨迹为规则的单一闭环，相图中仅含有1个周期运动，因此Poincare映射图对应为1个点。系统响应是周期的。

2.1.2 滞回碰摩力模型

当采用滞回碰摩力模型时，仍以转速为分岔参数，绘制分岔图（如图7所示）。对比图7和图4可见：首先，在滞回碰摩力作用下，系统的失稳速度(1226 rad/s)低于采用线性碰摩力模型得出的失稳速度(1476 rad/s)；其次，随着转速提高，系统始终作复杂的非线性运动，主要是拟周期运动，而未出现如图4所示的当转速加快到一定范围时恢复到周期1运动的情况。

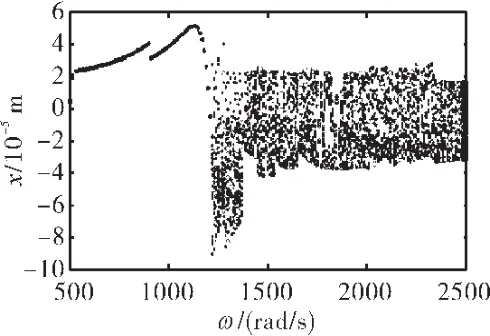
图7 转子响应分岔图（滞回碰摩力模型,ks=0.5×108N/m）

图8 转子系统响应（滞回碰摩力模型,ω=1800 rad/s）

图9 转子系统响应（滞回碰摩力模型,ω=2500 rad/s）

在ω=1800、2500 rad/s时，转子作拟周期运动，绘制时间历程曲线、轴心轨迹、相图和Poincare映射图，分别如图8、9所示。从图8、9中可见，时间历程曲线不是规则的周期运动，轴心轨迹和相图较为复杂，Poincare映射图呈现出1条闭环曲线。

2.1.3 2种模型的对比

与采用线性碰摩力模型相比，采用滞回碰摩力模型会使转/静子系统的振动特性变得更为复杂，也能够更真实地反映转/静子碰摩运动。

2.2 静子刚度对转子碰摩响应的影响

由于本文使用的滞回碰摩力模型是从微观的角度出发，诠释了转子与静子的碰撞嵌入过程。从碰摩力的表达形式可见，不同的静子刚度会直接影响转/静子的碰摩情况，有必要详细分析静子刚度对碰摩响应的影响。

图10 转子响应分岔图（滞回碰摩力模型,ks=1.0×108N/m）

图11 转子响应分岔图（滞回碰摩力模型,ks=1.5×108N/m）

图12 转子响应分岔图（滞回碰摩力模型,ks=2.0×108N/m）

给定其他参数，取静子刚度ks=0.5×108、1.0× 108、1.5×108、2.0×108N/m，求出转子转速从 500 ～2500 rad/s的响应，得到的分岔图分别如图 7、10～12所示。

对比图7、10～12给出的结果可知，随着静子刚度的增大，系统出现不规则运动的起始旋转速度也随之加快，虽然系统的振动幅值没有明显改善，但出现规则周期运动的区间却在不断加大。

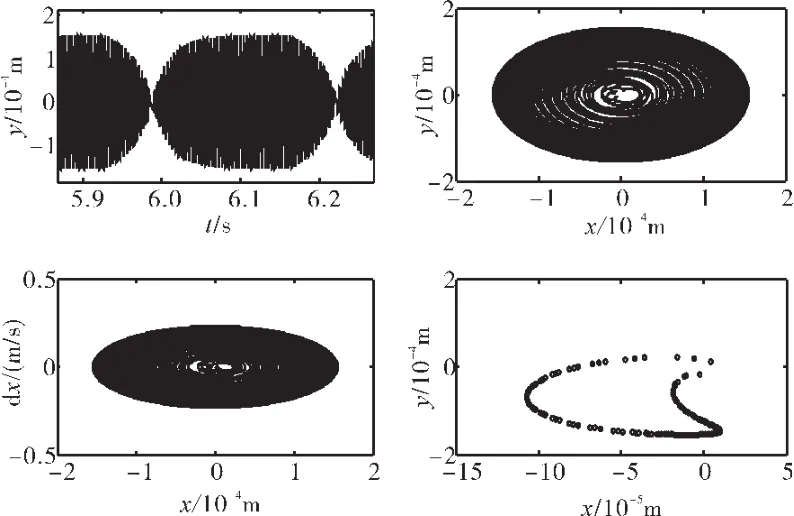
图13 转子系统响应（滞回碰摩力模型,ω=1800 rad/s、ks=0.5×108N/m）

图14 转子系统响应（滞回碰摩力模型,ω=1800 rad/s、ks=1.0×108N/m）

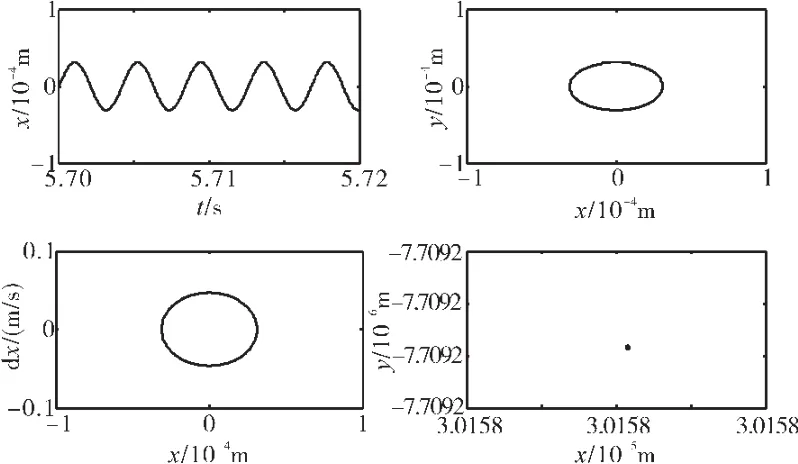
图15 转子系统响应（滞回碰摩力模型,ω=1800 rad/s、ks=1.5×108N/m）

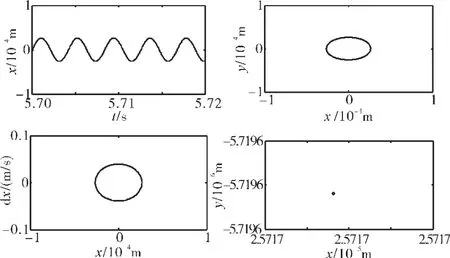
图16 转子系统响应（滞回碰摩力模型,ω=1800 rad/s、ks=2.0×108N/m）

为了进一步分析静子刚度对系统振动特性的影响，选取ω=1500、2000、2400 rad/s时，绘制4种刚度下的时间历程曲线、轴心轨迹、相图和Poinare映射图，如图13～16所示。

从图13中可见，在ks=0.5×108N/m时，系统作拟周期运动，这一点可以从Poincare映射图上清楚地看出，时间历程曲线出现了拍振现象；而在其他3种静子刚度下，系统作周期1运动。

给定转速ω=2000 rad/s，则在ks=0.5×108N/m（图17）和ks=1.0×108N/m（图18）时，转子作拟周期运动，其中如图17所示的时间历程曲线紊乱，而如图18的时间历程曲线为拍振；图19、20表明，随着转子刚度的增大，转子的运动变为稳定的周期1运动。

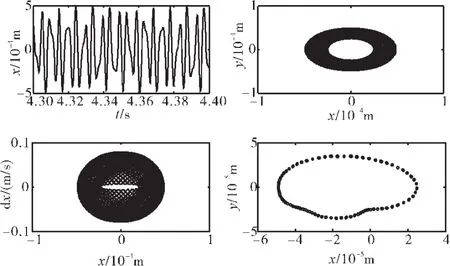
图17 转子系统响应（滞回碰摩力模型,ω=2000 rad/s、ks=0.5×108N/m）

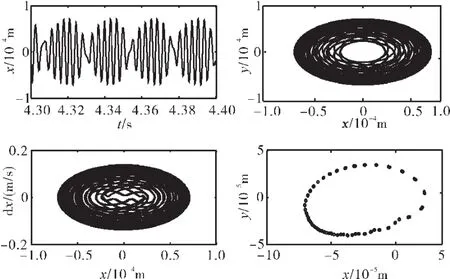
图18 转子系统响应（滞回碰摩力模型,ω=2000 rad/s、ks=1×108N/m）

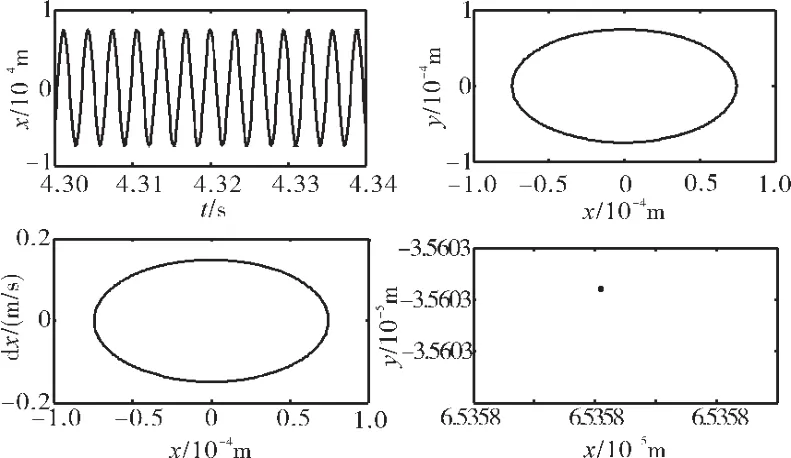
图19 转子系统响应（滞回碰摩力模型,ω=2000 rad/s、ks=1.5×108N/m）

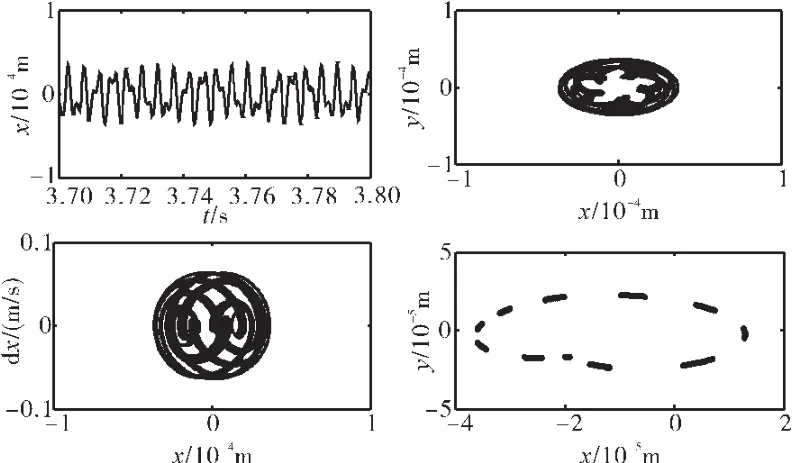
图21 转子系统响应（滞回碰摩力模型,ω=2400 rad/s、ks=0.5×108N/m）

图22 转子系统响应（滞回碰摩力模型,ω=2400 rad/s、ks=1.0×108N/m）

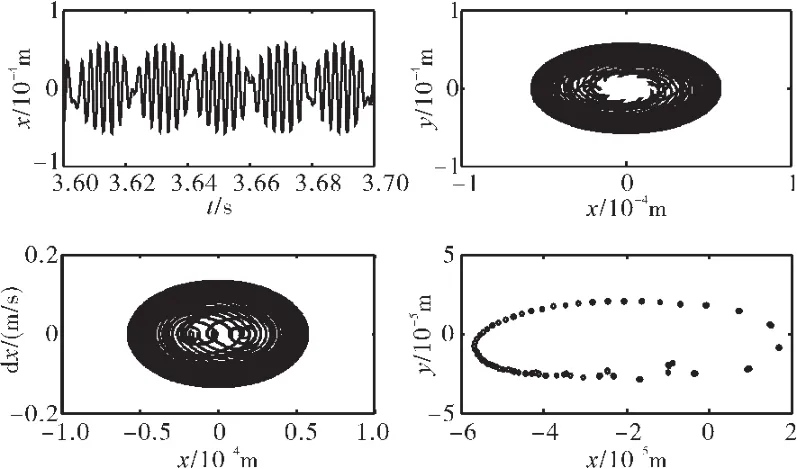
图23 转子系统响应（滞回碰摩力模型,ω=2400 rad/s、ks=1.5×108N/m）

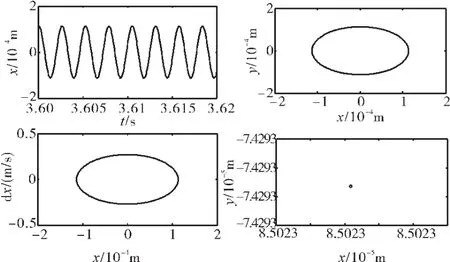
图24 转子系统响应（滞回碰摩力模型,ω=2400 rad/s、ks=2.0×108N/m）

当转速进一步加快到ω=2400 rad/s，则在ks=0. 5×108、1.0×108、1.5×108N/m（图23）时，转子作拟周期运动，转子系统的响应分别如图21～23所示；当转子刚度增大到ks=2.0×108N/m时，转子的运动变为稳定的周期1运动，其转子系统影响如图24所示。

2.3 转子偏心量对转子响应的影响

转子的偏心量会直接影响转子的偏心力，改变转子的振动幅值。同时，由于转/静子碰撞的嵌入位移与碰摩力相互影响，因此转子的偏心量与碰摩力间存在一定的耦合关系。

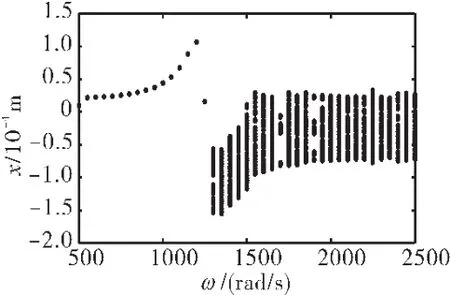
图25 转子响应分岔图（滞回碰摩力模型,e=2.0×10-5m）

图26 转子响应分岔图（滞回碰摩力模型,e=2.5×10-5m）

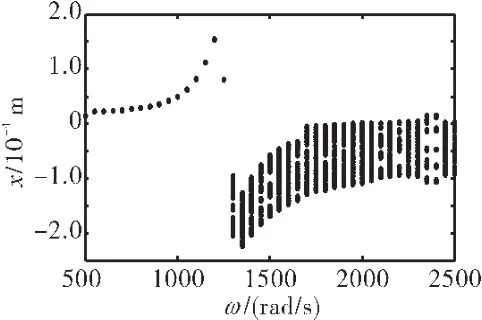
图27 转子响应分岔图（滞回碰摩力模型,e=3.0×10-5m）

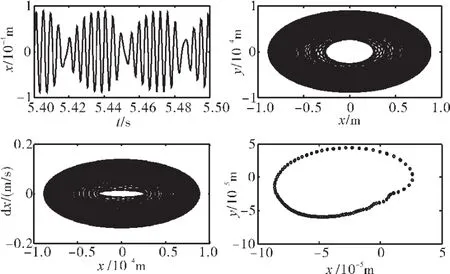
图28 转子系统响应（滞回碰摩力模型,ω=1600 rad/s、e=1.0×10-5m）

图30 转子系统响应（滞回碰摩力模型,ω=1600 rad/s、e=3.0×10-5m）

保持其他参数不变，令ks=0.5×108N/m时，以转速为分岔变量，在 e=1.0×10-5m、e=2.0×10-5m、e=2.5×10-5m、e=3.0×10-5m时，数值仿真得到的转子系统的响应分岔图如图7、25～27所示。

对比图7、25～27可见，在不同偏心量下，转子的横向振幅x发生了改变，但分岔图中的振动特性没有明显变化。以ω=1600 rad/s为例，分析转子的振动响应，如图28～30所示。

从图28～30中可见，在3种偏心量下，转子均作拟周期运动，时间历程曲线均呈现出拍振特点；随着偏心距的增大，拍振的现象变得不明显；对比各偏心量下的轴心轨迹图可知轴心轨迹的多重闭环半径随着偏心量的增加而增大；相图中闭环曲线的半径也逐渐增大，说明偏心量的增加会使横向振动位移增大。

3 结论

转/静子碰摩力模型的建立是包括航空发动机转子在内的旋转机械研究中亟待解决的重要基础问题。本文重点比较了滞回碰摩力模型和几种经典的碰摩力模型，并以Jeffcott转子为典型例子，比较了基于滞回碰摩力模型和线性碰摩力模型得到的系统碰摩响应，得到如下结论：

（1）滞回碰摩力模型摒弃了以往碰摩力模型的准静态假设，包含了静子结构刚度、碰撞前速度等物理因素，体现了碰撞动刚度、接触阻尼等因素的影响。其动刚度、速度指数等是根据试验拟合而得的，能够准确地反映其物理实质；

（2）与采用线性碰摩力模型所得的结果相比，采用滞回碰摩力模型会使转/静子系统的振动特性变得更为复杂，也能够更真实地反映转/静子碰摩运动；

（3）静子刚度会直接影响转子系统的碰摩响应，从通过数值计算所绘的不同静子刚度下的分岔图可知，增大静子刚度会抑制转/静子碰摩过程中出现复杂非线性现象，使转子在较宽的转速范围内作周期1运动；转子的偏心量会影响振动幅值，但对系统的振动形态影响较小。

[1]江俊，陈艳华.转子与定子碰摩的非线性动力学研究[J].力学进展，2013，43（1）：132-148. JIANG Jun,CHEN Yanhua.Advances in the research on nonlinear phenomena in rotor/stator rubbing system [J].Journal of Advances in Mechanics,2013,43（1）: 132-148.（in Chinese）

[2]Schwab A L,Meijaard J P,Meijers P.A comparison of revolute joint clearance models in the dynamic analysis of rigid and elastic mechanical systems[J].Mechanism and Machine Theory,2002,37:895-913.

[3]刘才山,陈滨.多柔体系统碰撞动力学研究综述[J].力学进展,2000,30（1）:8-14. LIU Caishan,CHEN Bin.A global review for the impact dynamic research of flexible multibody systems[J].Advances in Mechanics,2000,30（1）:8-14.（in Chinese）

[4]Flores P,Leine R,Glocker C.Modeling and analysis of planar rigid multibody system with translational clearance joints based on the non-smooth dynamics approach[J]. Multibody Systems Dynamics,2010,23:165-190.

[5]Yigit A S,Ulsoy A G,Scott R A.Dynamics of a radially rotating beam with impact,part1:theoretical and computationalmodel[J].JournalofVibration and Acoustics,1990,112:65-70.

[6]Nagaraj B P,Nataraju B S.Dynamics of a two-link flexible system under going locking:mathematical modelling and comparison with experiments[J].Journal of Vibration and Vibration,1997,207（4）:567-589.

[7]Gilardi G,Sharf I.Literature survey of contact dynamics modeling[J].Mechanism and Machine Theory,2002,37: 1213-1239.

[8]金栋平,胡海岩.碰撞-振动及其典型现象 [J].力学进展, 1999,29（2）:155-164. JIN Dongping,HU Haiyan.Vibro-impactsand their typical behaviors of mechanical systems[J].Advances in Mechanics,1999,29（2）:155-164.（in Chinese）

[9]Hertz H.On the contact of elastic solids[J].Journal of Fur Die Reine Angewandte Marhematik,1881,92: 156-171.

[10]Machado M,Moreira P,Flores P,et al.Compliant contact force models in multibody dynamics:evolution of the Hertz contact theory[J].Mechanism and Machine Theory,2012,53:99-121.

[11]Hunt.K H.Crossley F R.Coefficient of restitution interpreted as damping in vibroimpact[J].Journal of Applied Mechanics,1975,42:440-445.

[12]Herbert R G,Whannell D C.Shape and frequency composition of pulses from an impact pair[J].Journal of Engineering for Industry,1977,99:513-518.

[13]Dubowsky S,Freudenstein F.Dynamic analysis of mechanical systems with clearance,Part 1:formation of dynamic model[J].ASME Journal Engineering for Industry,1971,93B:305-309.

[14]Dubowsky S.Gardner T N.Dynamic interactions of link elasticity and clearance connections in planar mechanical systems[J].ASME Journal of Engineering for Industry,1975,97B（2）:652-661.

[15]曹登庆，初世明，李郑发，等.空间可展机构非光滑力学模型和动力学研究[J].力学学报,2013,45（1）:3-15. CAO Dengqing,CHU Shiming,LI Zhengfa,et al.Study on the non-smooth mechanical model and dynamics for space deployable mechanism[J].Chinese Journal of Theoretical and Applied Mechanics,2013,45（1）：3-15.（in Chinese）

[16]陈果.航空发动机整机耦合动力学模型及振动分析[J].力学学报,2010,42（3）:548-559. CHEN Guo.Coupling dynamic model and dynamic analysis for whole aeroengine[J].Chinese Journal of Theoretical and Applied Mechanics,2010,42（3）: 548-559.（in Chinese）

[17]陈果.航空发动机整机耦合动力学模型及其验证[J].航空动力学报,2012,27（2）:241-254. CHEN Guo.A coupling dynamic model for whole aeroengine vibration and its verification[J].Journal of Aerospace Power,2012,27（2）:241-254.（in Chinese）

[18]杨树华，杨积东，郑铁生，等.基于Hertz接触理论的转子碰摩模型[J].力学学报,2013,20（4）:61-65. YANG Shuhua,YANG Jidong,ZHENG Tiesheng,et al. A new rotor-statorrubbing modalusing Hertzian impact-contact theory[J].Chinese journal of Applied Mechanics,2013,20（4）:61-65.（in Chinese）

[19]曹登庆，陈华涛，初世明，等.转子-弹性机匣系统碰摩的碰摩力表征与实验研究 [R].哈尔滨：哈尔滨工业大学，HIT-VDC-2013-02. CAO Dengqing,CHEN Huatao,CHU Shiming,et al. Rub-impact force model for the rub-impact rotor with elastic cases and its experimental investigations[R]. Harbin:HIT Report,HIT-VDC-2013-02.（in Chinese）

[20]陆启韶，张思进，王士敏.转子-弹性机壳系统碰摩的分段光滑模型分析[J].振动工程学报,2000,13（2）:178-187. LU Qishao,ZHANG Sijin,WANG Shimin.Analysis to a piecewise-smooth model of rub-impact rotor system with elastic cases [J]. Journal of Vibration Engineering,2000,13（2）:178-187.（in Chinese）

[21]陈巍，杜发荣，丁水汀.超高速转子系统动力学特性(Ⅱ):碰摩转子[J].推进技术,2012,33（6）:865-874. CHEN Wei,DU Farong,DING Shuiting,etal. Research on dynamic characteristic for a super-high speed rotor system,Ⅱ:rotor system with rubs[J]. JournalofPropulsion Technology,2012,33（6）: 865-874.（in Chinese）

[22]秦志英，陆启韶.基于恢复系数的碰撞过程模型分析[J].动力学与控制学报,2006,4（4）:294-298. QIN Zhiying,LU Qishao.Analysis of impact process model based on restitution coefficient[J].Journal of Dynamic and Control,2006,4 （4）:294-298.（in Chinese）

Study on Rub-impact Responses of Rotor Systems Based on Hysteretic Rub-impact Force Model

CAO Deng-qing1，YANG Yang1，WANG De-you2,CHEN Hua-tao1,JIANG Guang-yi2
（1.School of Astronautics,Harbin Institute of Technology,Harbin 150001,China;2.AVIC Shenyang Engine Design and Research Institute,Shenyang 110015,China）

The rub-impact of rotor/stator is one of the major factors for the stability and safety of rotating machine,while the characterization of the rub-impact force is a key problem in the prediction of dynamical responses of the rotor system.The applicable scope of the existing rotor/stator rub-impact force models was discussed,the physical significances of the hysteretic rub-impact force model was described clearly,and the comparison between the hysteretic rub-impact force model and classical ones was conducted.Taking the Jeffcott rotor as a typical example,the rub-impact responses of system based on the hysteretic rub-impact force model are given and used to compare with the result form the system with linear rub-impact force model.The effects of stator stiffness and the rotor eccentricity on rubimpact responses of the rotor system with the hysteretic rub-impact force model were given to analyze by the numerical results.The numerical simulation results show that the stability threshold speed (1226 rad/s)of the system in terms of the hysteretic rub-impact force model is less than that(1476 rad/s)of the system with linear rub-impact force model,and the dynamic characteristics are more complicated, therefore,the essential physical property of rub-impact can be reflected more veritably.

Jeffcott rotor;rub-impact;linear model;Hertz model;hysteretic model

V 23.9

A

10.13477/j.cnki.aeroengine.2014.01.001

2013-09-04 基金项目：国家重大基础研究项目资助

曹登庆（1958），男，教授，主要研究方向为转子动力学、复杂系统动力学与振动控制；E-mail:dqcao@hit.edu.cn。

曹登庆，杨洋，王德友，等.基于滞回碰摩力模型的转子系统碰摩响应研究 [J].航空发动机，2014，40（1）：1-9.CAO Dengqing，YANG Yang，Wang Deyou，et al.Study on the Rub-Impact Responses of Rotor Systems Based on the Hysteretic Rub-Impact Force Model[J]. Aeroengine，2014，40（1）：1-9.