变压器局放超声检测和定位技术现状及发展
2014-07-06刘化龙
刘化龙
(武汉大学电气工程学院,武汉 430072)
电力变压器是电力系统中最为重要的设备之一,其工作状态决定了电力系统能否安全稳定地运行。事故或者非计划的变压器停运能造成严重的后果和巨大的经济损失。变压器的安全稳定运行与其绝缘状况有着直接联系,而局部放电则是导致变压器绝缘劣化或击穿的主要原因之一[1-6]。局部放电通常是指绝缘介质多少可能会存在着某些绝缘弱点,当外施电压超过阀值电压时,它会首先发生放电,但并不随即扩大至整个绝缘介质,这种仅限于弱点处的放电叫做局部放电。局部放电能够暗示绝缘缺陷,所以局部放电的早期发现有助于合理安排的检修,从而避免因绝缘击穿造成的巨大经济损失。
基于局部放电发生时的各种物理和化学现象,产生了各种对局部放电检测和定位的方法。大体可分为电气检测与定位法和非电检测与定位法。目前,超声波检测与定位法是国内外研究最多与应用最广泛的检测与定位方法之一。
相比其他定位法,超声波法有很多独有的优势。本文系统地阐述了各种超声波定位方法,并探讨了超声法在局部放电检测和定位中存在的问题及其发展方向。
1 局部放电产生超声波的原理与超声波在变压器中的传播规律
1.1 局部放电产生超声波的原理
目前,国内外已有相当多的文献研究如何用超声波信号定位变压器内部的局部放电源。然而,对变压器局部放电产生超声波的机理和传播规律的研究并不多。为了更好地运用超声波来检测和定位局部放电源,对局部放电产生超声波的机理和传播规律的研究显得尤为重要。
在变压器中,只要存在局部放电,随着放电的发生,在放电过程中就会伴随着崩裂状的声发射,产生超声波,且很快向四周传播[2,6-14]。
绝缘介质中产生局部放电的原因很多,放电形式也多种多样,因此放电过程很复杂。然而,变压器油中的气泡或其固体绝缘介质中的气隙是变压器局部放电通常发生的场所。因此,本文主要阐述变压器油中气泡发生局部放电时产生超声波的原理。
波起源于振动,具有弹性和惯性的力学系统都具有振动的能力。当变压器内部的绝缘介质发生局部放电时,由于气泡受到电场力或压力的作用,会发生膨胀和收缩的过程,这将引起局部体积的变化。局部体积的变化将在外部产生超声波。
当过电压很低时,某些局部放电几乎不向外辐射热量;当过电压很高时,另外一些局部放电则可能向外辐射很高的热量。变压器内部的绝缘介质发生局部放电时,气泡处于一定的电场中,这时气泡带有一定的电荷,因此气泡会受到电场力的作用。在局放向外辐射很高热量的情况下,电弧电流会在放电通道中产生高温,此高温会使气泡膨胀而受到一定的压力。因此,气泡产生超声波主要受2个因素影响:其一为局放瞬时气泡所承受的电场力;其二是局放产生后所发出的热量使气泡扩张,这样气泡将承受压力的作用。
当过电压较低时,承受电场力的气泡会形成振幅慢慢减小的振荡运动,进而超声波会在周围的绝缘介质中产生。当过电压较高时,气泡将发生放电,进而被击穿,从而产生细微的线度参差不齐的放电路径,放电路径内的气体受到强烈的电离与加热,气体的加热引起放电路径的膨胀,进而使气泡受到压力,从而在绝缘介质中产生超声波。
实际上,变压器内部绝缘介质的局部放电中超声波的产生通常是上述两种因素联合作用的结果。
1.2 局部放电声发射的频谱范围
由于局部放电持续时间很短,故局部放电产生的声波频谱较宽,可达到数兆赫兹,甚至数十兆赫兹。
另外,变压器噪声和局放超声信号的频带不同,这非常有利于区分噪声和超声信号。
1.3 超声波在变压器中的传播规律
局部放电产生的超声波信号在内部结构非常复杂的变压器中会通过不同的传播路径向外部传播,通常要经过多层介质才能到达传感器所在的位置。
声波的强度与局放源所释放的能量成正比,所以声波的幅值与局放能量的平方根成正比,这表明声波的幅值与放电的强度存在线性关系。当声波通过绝缘介质传播时,随着与局放源距离的增加,波的强度逐步减小。特别是经过多次界面折、反射和沿变压器器壁钢板的传播,声信号衰减更为严重。
根据介质的声特性阻抗,在不同介质的边界表面会发生声波的反射、折射、偏向以及衰减。通常声波传输衰减的主要原因有3个:一是由声束扩散所引起的衰减;二是由散射所引起的衰减;三是由介质的吸收所引起的衰减。对于超声波来说,声压衰减规律可简单地表示为

式(1)中:P0为超声波刚入射到液体上时的声压;P为超声波在液体中传播一段距离后的声压;α为超声波的衰减系数。
变压器局部放电产生的超声波在变压器油中传播时,由于质点的振动方向与超声波的传播方向平行,故为纵波。然而,当超声波在变压器器壁等固体中传播时,则会存在质点的振动方向与超声波传播方向平行的纵波和质点的振动方向与超声波传播方向垂直的横波。
超声波的入射、反射及折射都遵循斯奈尔法则,即

式(2)中:θ1与v1分别为入射波形的角度与速度;θ2与v2分别为折射波形的角度与速度。当v1<v2时,θ1< θ2;当 θ2=90°时,发生全发射,此时的 θ1称为临界角。局部放电源产生的超声波在变压器油中以纵波形式传播,当遇到油箱钢板界面时会折射出纵波和横波。相应地,临界角有2个,纵波临界角θcp=arcsin(voilvp),横波临界角θcs=arcsin(voilvs),其中:voil为油中声速;vp,vs分别为钢板中纵波波速和横波波速。常温下,voil,vp和vs可分别取 1 415 m/s,5 900 m/s 和 3 200 m/s,则临界角θcp≈13.88°,θcs≈26.24°。
在各向同性介质中,超声波的传播遵循标准偏微分方程,即

式(3)中:P是声压(Pa);t是时间(s);v是声速(m/s)。
局部放电产生的超声波通过周围的油和绝缘介质传播,并且能通过传感器在变压器外壳上检测到[9,10,12,15-17]。传感器所检测到的超声波信号波形不仅取决于局放源、波速、传播路径,而且取决于波传播所经过的介质和所用的传感器。典型的超声波信号波形如图1所示。
超声波传播过程中所发生的反射、折射和介质对波的吸收等都将导致波传播路径的改变。
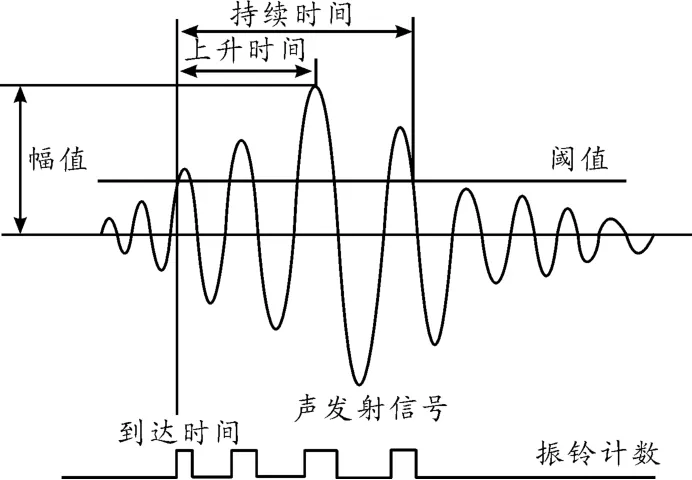
图1 典型的声发射信号波形
变压器内部的绝缘介质发生局部放电时产生的超声波到达位于变压器器壁的超声传感器有2条基本路径:其一为直接传播的直接路径(SA);其二是超声波先传播到变压器油箱内壁,然后沿钢板传播到超声传感器的复合路径,如图2所示。

图2 变压器内超声波传播路径模型
由图2可见:直接路径只有一条,而复合路径却有多条,即B可以改变。在局放源S产生的超声波中,SA为纵向波(直达波),SBA,SCA与 SDA为复合波。
局放源产生的球面波可视为由该源产生并向各个方向传播的无数个声波,每一个声波以不同的入射角θ到达油箱壁。由于钢板中的声速比油中的声速更高,所以直接路径并不一定是最快的路径。由图2中箭头所示的路经可知,声波传播到传感器所需的时间为
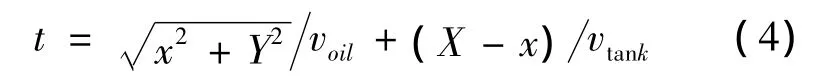
式(4)中:vtank为钢板中横波或纵波的速度。令dt/dx=0,便可求出传播时间最短的路径,此时θ刚好等于临界角θc,且θc=arcsin( voil/vtank)。故最短的传播时间为

式(5)中,仅当 φ>θc时成立。若 φ≤θc,直接路径(即SA)为传播时间最短的路径。直接路径的传播时间为

一般而言,声波的传播速度取决于周围的介质。但温度对油中的声速有影响[12,18]。印度学者Shanker[12]等指出:局放产生的声波在油中的传播速度取决于温度与油压,同时给出了在大气压为685 mmHg,温度从30℃到75℃时,速度随温度变化的经验公式,即

式(7)中:t为油温(℃);v为油中声速(m/s)。根据式(7)及文献[18]可知:当温度从30℃到75℃时,变压器油中的声速降低。
2 超声波定位法原理及分类
2.1 超声波定位法原理
变压器局部放电产生的超声波传播到固定在变压器油箱外壁上的超声传感器时,通过超声传感器的压电元件将超声波信号变换为电信号,而后再通过放大滤波步骤后输出到计算机定位系统中进行信号处理、诊断和定位,进而定位出局放源的位置,此即为超声波定位法的原理,如图 3所示。
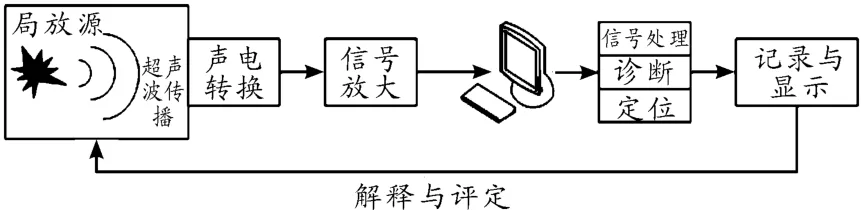
图3 超声波定位法基本原理
超声波定位较其他方法有很多优势,主要表现在[3,7-10,19-21]:① 非破坏性且抗干扰能力强(对不检测电信号的声-声定位法而言);② 可同时检测和定位局放且定位能力强、精度高;③稳定性好且成本低;④可进行在役、实时、连续监测。
2.2 分类
根据不同的时间基准,超声定位可分为两大类:电-声定位法与声-声定位法。它们的区别在于电-声法以电脉冲信号为零时间点获取至传感器的超声波传播时间,进而基于球面定位(三角定位)法计算局放源的位置;声-声法则根据各传感器接收到超声波信号的相对时延来定位局部放电源的空间位置。
具体而言,超声定位法有球面定位法(三角定位法)、V型曲线法(最小时延法)、双曲面法、顺序定位法和模式识别法等。
2.2.1 球面定位法(三角定位法)
为简便起见,以变压器的一个角为原点O(0,0,0)建立空间直角坐标系,局放源用 P(x,y,z)表示,各个传感器分别用 S1(x1,y1,z1),S2(x2,y2,z2),S3(x3,y3,z3)和 Sn(xn,yn,zn)表示,如图 4所示。
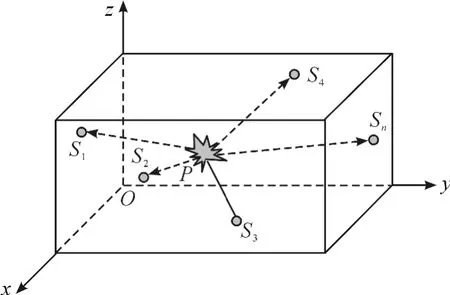
图4 局放源和传感器位置原理图
1)基于电-声的球面定位法
局放产生的电信号的传播速度远大于声信号,因此可忽略电信号的传播时间,认为它们之间的时差即为声信号从局放源传播到传感器的时间。这样,可以建立如下球面定位方程组[3,10,20-25]:
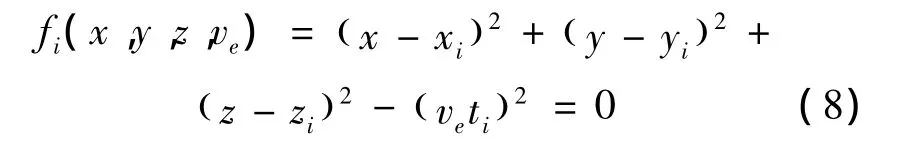
式(8)中:i=1,2,3,…,n,ve为等值声速(通常以最短路径计算的首波声速称等值声速)。该式的物理意义为:局放源位于以各传感器为球心,veti为半径的球面上,因此各球面的交点就是放电源的位置。式(8)的物理意义在于为基于电-声的球面定位法提供了一种作图的算法。虽然该算法基本概念清晰、现场实用性强,但精度不高。
从理论上说,基于电-声的球面定位法至少需要3个传感器。但是由于超声波的传播路径比较复杂,故各路径的等值声速一般不尽相同且不易获得,所以在实际应用中一般以等值声速为变量。因此,实际运用中至少需要4个传感器。
2)基于声-声的球面定位法
若首先接收到超声波信号的传感器为1号传感器,用τi1=ti-t1表示i号传感器与1号接收超声波信号的时差。则可建立n-1个定位方程组[10,19,21,23,26-29]:

3)最优解的求取方法
一般而言,式(8)和(9)为超定方程组,没有精确解,只能求取其最优解。为求出局放电源,则可等效为最小,则局放超声波定位变成一个约束性最优化的问题,即
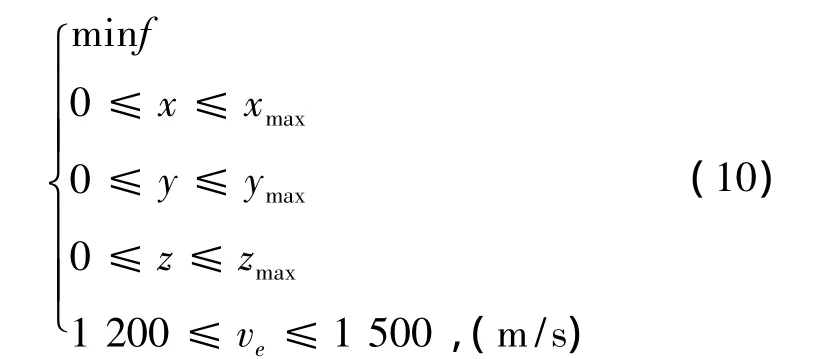
式(10)中:xmax,ymax,zmax为变压器的等效长、宽、高。等值声速一般取1 200 m/s≤ve≤1 500 m/s。
方程组(10)有很多解法,最常用的是最小二乘法[4,20-21,23],但其存在局部收敛等缺陷。
为了克服最小二乘法局部收敛的缺陷,出现了线性算法[30]、模糊聚类(fuzzy clustering)算法[3]、粒子群优化(PSO-Particle swarm optimization)算法[26-27]、混沌搜索的 PSO 算法[31]、模拟退火算法[27]和遗传算法[2,27,29]等。其中,模拟退火算法、遗传算法、粒子群算法属于现代智能算法;相比于传统算法,他们方便搜寻全局最优[27]。
遗传算法的最大优势是不需要估计初始值,且能防止结果陷入局部最小,结果优于最小二乘法。文献[27]通过与传统算法相比较,提出了线性策略粒子群的智能优化算法,并从算法上验证了其是最优越的定位算法,且与实践吻合较好。文献[24]和[30]提出了线性非迭代的算法,该方法不存在收敛问题,且计算量小、速度快、不会得出远离局放源的点或无解的情况。模糊聚类算法精度高、抗干扰且可操作性强,而且可用于多局放源的定位。
另外,也有把基于声-声的球面定位方程转化为无约束条件下的最优化问题,即目标函数为[32-33]:

文献[33]提出了一种处理无约束优化问题的自适应优化算法,该算法具有较好的自适应性和较高的精度。
2.2.2 V型曲线法(最小时延法)
这种定位法基于电-声触发的定位原理。其基本思想是:在局放源周围临近范围内,在横向和纵向2个相互垂直的方向上将超声传感器沿变压器器壁分隔排列,每个方向取不少于9个点。把沿外壳分隔测量点的距离值作为纵坐标,而把局部放电源产生的超声波到达各点的相应时间作为横坐标,这样可以作出相应的曲线,此曲线成V形。V型曲线的顶点就是距离局部放电源的最近点,此点对应的超声波信号的传播时间即局部放电源产生的超声波通过直接路径传播到变压器器壁此点的时间。将此时间与直达波传播途径所对应的时间相比较,即可得出局放源的位置。
V型曲线法的优点是简单直观、作图方便且不计声速[21,34]。
2.2.3 双曲面法
该法基于声-声触发的定位原理,其基本思想是:选取传感器S1(x1,y1,z1)作为参考基准传感器,并测量局部放电超声信号传播到其他传感器所对应的相对时延。把这些相对时延代入特定的方程组中联立求解,则可定位出局部放电源的空间位置。因此,若设传感器Si(xi,yi,zi)与参考传感器 S1(x1,y1,z1)的相对实测时间差为 τn(i=1,2,…,n;n≥4,这表明该法至少需要4个传感器;但若放电点在复合介质中,如线圈内部,则至少需要5个传感器),则相应超声波信号的传播时间差为 τi1=ti-t1。
根据超声信号到达传感器Si(xi,yi,zi)与参考传感器S1(x1,y1,z1)的传播距离差,可得双曲面方程如下[20,21,23,35]:
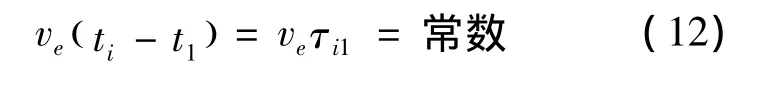
式(12)的几何意义为:局放源 P(x,y,z)位于以Si,S1为焦点,以所测超声波信号到达传感器的相对时差为一定值的双曲面上,这些双曲面相交的交点就是局放源的空间位置。
假设ve为已知的定值(若假定ve为变量,则需要多用一个传感器),则局放源P(x,y,z)到传感器 Si的声传播时间为[20-21,23,35]:

如果同时测出n-1个相对时间差,且已知等值声速ve及各传感器坐标,则联立式(12)、(13)得局放源的空间位置。
2.2.4 顺序定位法
如图5所示,顺序定位法基于局部放电源产生的超声波到达不同超声波传感器的秩序(传感器位置的差异性使得它们接收到局放源传来的超声波信号的秩序不一致)而定出大致的局部放电区域,但其不能提供准确的局部放电源的空间位置。该定位法的具体操作流程为:将一组超声传感器放置在变压器器壁的一个面上,当局部放源产生的超声波信号到达这一平面时,如果某超声传感器(不妨设为传感器1)最先收到超声波信号,由传感器1与其周围的超声传感器的垂直平分线所围成的区域称为主区;而后如果超声传感器2接收到超声波信号,再根据以上的垂直平分线分割的原理,可确定出子区域2;随后如果超声传感器3接收到超声波信号,则可确定出子区域3,……。依此类推,则可大致断定出局部放电源所在的区域。
2.2.5 模式识别法
该方法基于声-声触发原理。假设变压器安装了n个传感器(其中传感器1为基准传感器),且设与 fi(k=1,2,…,m)分别为标准模式矢量与待判定模式矢量,则两者的欧式相对距离为
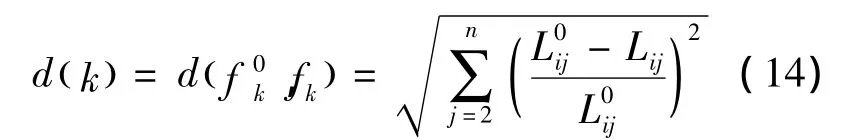
若将d(k)从小到大依次排序,处于首位的与的距离最小。
不妨将变压器模块化,即设变压器由m个子模块组成。任何一个空间坐标(x,y,z)已知的子模块k,其与传感器i的距离为:
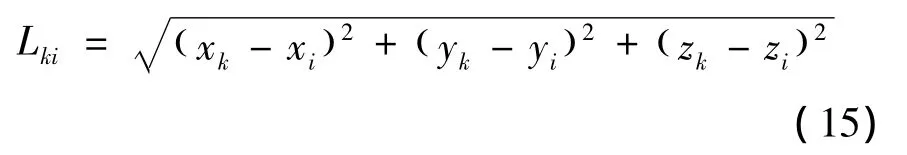
式(15)中,i=2,…,n,则子模块 k 的待判断模式矢量为 fk= ( Lk2,…,Lki,…,Lkn)。超声波从子模块k传到基准传感器1的时间T由球面方程易得,而通过设备可测得各延迟时间 τ21,τ31,…,τn1;又局放源与传感器i的距离可由=ve( T +τi1)计算得到,其中ve为等值声速。这样便可求出标准模式矢量f= ( L,…,L,…,L)。再根据公式(14)可依次计算出d(1),d(2),…,d(m),这些欧式相对距离的最小值所对应的变压器的子模块很有可能是局部放电源所在的空间位置。
该定位方法具有精确度高、通用、实现简单等优点。

图5 顺序定位法原理图
2.3 各种局部放电定位法的评述
球面定位和双曲面定位两种定位方法分别适用于不同的定位情况。当现场电气干扰较大时,或对运行中的变压器进行局部放电定位时,可采用双曲面定位。V形曲线法的方法简单,容易操作,且不计声速,但仅能给出局放源距油箱壁参考点的大概距离。
3 与其他方法的联合
3.1 超声法的误差分析
虽然研究者已经对超声法做了大量的工作和研究,采用了多种定位方法,且定位方案成熟,但其定位效果有时仍不是非常精确。造成这种现象的主要原因包括:
1)时间(时延)测量的精确性不高
当采用电-声法时,由于电磁干扰的影响,势必造成电信号的难以确定,从而时间测量的精确性不高,进而影响定位精度。
2)传播途径影响
当变压器内部产生的超声波传播路径出现复合路径时,则超声波传感器不容易检测到此类超声波信号,从而影响到局放源的精确定位。
3)定位算法问题
求解曲面方程通常所采用的最小二乘法具有局部收敛等缺陷,容易产生无解。
4)传感器的影响
位于变压器器壁的超声传感器不一定能准确地接收超声信号,所以应加强对传感器的研究,提高其灵敏度。
5)直达波确定的准确性
直达波的确定在超声法中非常重要。但是目前对于超声直达波的研究很少,技术人员主要凭经验来排除非直达波,这样必然会影响直达波确定的准确性。
3.2 超声法的局限性
1)多用于单一源的定位
目前,超声法主要用于单一局放源的定位。
2)不能判断局放的严重性
变压器局部放电的超声波信号不足以评估局放的严重性。
3)主要用于油浸式变压器
超声法检测和定位干式变压器局放的应用和研究较少。
4)主要用于交流网络中的变压器
超声法检测和定位HVDC输电网络中换流变压器局放的应用和研究较少。
3.3 超声法与其他方法的联合
由于超声法的上述不足,同时为了增加最终诊断的可靠性,出现了超声法与其他方法的联合检测。
3.3.1 超声波与特高频的联合
特高频(UHF)法是目前局部放电检测的一种新方法。该方法通过天线传感器接收局部放电过程中辐射的特高频电磁波,从而实现局部放电的检测与定位。
通过特高频与超声波联合检测和定位可以解决现场难以获得电信号的问题。
基于特高频和超声波联合的局部放电定位法与超声波电-声检测法的原理相似,它以特高频信号取代电流脉冲信号,检测变压器内部绝缘介质发生局部放电时产生的特高频与超声波信号;以局放产生的特高频信号为时间基准,由此计算出超声波信号相对于特高频信号的相对时延,进而定位出局放源的空间位置。
3.3.2 超声波与射频的联合
射频检测法属于高频局部放电测量,其检测频带已达甚高频(VHF)范围,测量频率达30 MHz。
基于射频和超声波的局部放电联合检测与定位法以射频信号代替电流脉冲信号,进而基于射频信号与超声波信号来定位局放源的空间位置。该方法不仅传承超声波法便于定位的优势,而且具有射频检测法能迅速检测出局部放电的高灵敏度。同时,该联合检测与定位法还可简化定位流程,提升检测系统的抗干扰能力与定位的实时性。
超声-射频电流联合检测与定位法具有以下优点:①检测和定位的灵敏度较高;② 抗噪声的能力更好;③可以迅速和便利地对变压器内部绝缘介质局部放电进行检测和定位,流程相比超声法更加简便;④为非接触检测与定位法,可以实现在役、实时监测;⑤超声波与射频联合检测与定位法可以取代电-声检测与定位法。
3.3.3 超声波与光的联合
超声波-光联合检测与定位法通过光纤传感器,利用光纤自身或外部敏感元件将超声波信号变换为光强度的变化,然后通过光敏元件把光强度的变化转换成电信号;最后通过类似于超声波检测与定位法的原理来检测和定位局放源的空间位置。
该方法可以克服超声波检测与定位法易受到电磁干扰等环境噪声影响的缺陷。
另外,除了上述提及的联合检测和定位法,文献[36]介绍了一种基于暂态对地电压和超声阵列信号的变压器局放定位方法。
4 总结与展望
超声法由于其独有的优势,特别是与其他方法联合,必然会得到更加广泛的运用。但为了克服超声法的上述局限性,应重点加强以下几方面的研究:
1)加强对变压器超声波产生机理、传播规律(特别是当局放发生于绝缘深部隐蔽位置时)和信号的衰减及折射等方面的基础研究。
2)加强对传感器的研究,特别是变压器内置传感器和传感器阵列,并对已有传感器进行优化。在线监测通常在电磁干扰极其严重的环境下进行,只有抗干扰能力强、灵敏度高的传感器才能够探测到真实可信的信号,从而实现精确的定位。
3)加强局放所产生的电与声信号处理的研究,深入地把数字信号处理技术及计算机技术引入到局放的超声波检测和定位中,进一步探索如何更好地去除噪声,提高信噪比。
4)加强对直达波和复合波识别的研究。
5)加强超声波法与其他定位法联合的研究,进而博采众长,提高定位精度。
6)加强对多局放源超声波定位技术的研究。目前超声波法主要用于单局放源的定位,而在生产实际中,往往多局放源并存,故研究多局放源定位非常有意义,有助于对变压器状态做出更准确的评价。
7)加强超声波定位法及其联合定位法现场应用的研究。
8)加强对干式变压器和承受直流电压的HVDC输电网络中换流变压器局放的超声波检测和定位的研究。
[1]Ashraf S A,Stewart B G,Chengke Zhou,et al.Modelling of Acoustic Signals from Partial Discharge Activity[C]//GCC Conference(GCC).Manama:IEEE,2006:1-5.
[2]Veloso G F C,da Silva L E B,Lambert-Torres G,et al.Localization of Partial Discharges in Transformers by the Analysis of the Acoustic Emission[C]//IEEE ISIE 2006,Montreal:IEEE,2006:537-541.
[3]Du B X,Lu Y H,Weil G Z,et al.PD Localization Based on Fuzzy Theory Using AE Detection Techniques[C]//2005 Annual Report Conference on Electrical Insulation and Dielectric Phenomena.[S.l]:IEEE,2005:449-452.
[4]Rubio-Serrano J,Posada J,Bua I,et al.Comparison of Processing Techniques for Optimizing the Diagnosis of Solid Insulation Based on Acoustic Emissions from Partial Discharges[C]//2013 IEEE International Conference on Solid Dielectrics.Bologna:IEEE,2013:129-132.
[5]Howells E,Norton E T.Detection of Partial Discharges in Transformers Using Acoustic Emission Technique[J].IEEE Transactions on Power Apparatus and Systems,1978,PAS-97(5):1538-1549.
[6]Venkatesh A S P,Danikas M G,Sarathi R.Understanding of Partial Discharge Activity in Transformer Oil under Transient Voltages Adopting Acoustic Emission Technique[C]//2011 6th International Conference on Industrial and Information Systems.Sri Lanka:IEEE,2011:98-101.
[7]Cheng-Chien Kuo.Particle Swarm Trained Neural Network for Fault Diagnosis of Transformers by Acoustic E-mission[C]//Proceedings of 2007 3rd International Conference on Intelligent Computing.Qingdao:Springer-Verlag,2007:992-1003.
[8]Lundgaard L E.Partial Discharge-Part XIV:Acoustic Partial Discharge Detection-Practical Application[J].IEEE Electrical Insulation Magazine,1992,8(5):34-43.
[9]Menon R,Kolambekar S,Buch N J,et al.Correlation of Acoustic Emission Method and Electrical Method for Detection of Partial Discharges in Transformers[C]//2001 IEEE 7th International Conference on Solid Dielectrics.Eindhoven:IEEE,2001:299-302.
[10]Mohammadi E,Niroomand M,Rezaeiarr M,et al.Partial Discharge Localization and Classification Using Acoustic Emission Analysis in Power Transformer[C]//2009 31st International Telecommunications Energy Conference.Incheon:IEEE,2009:1-6.
[11]Samsudin M R,Ramli A Q,Berhanuddin A,et al.Incipient Fault Detection in 33/11kV Power Transformers by Using Combined Dissolved Gas Analysis Technique and Acoustic Partial Discharge Measurement and Validated Through Untanking[C]//2010 Proceedings of the International Symposium on Modern Electric Power Systems.Wroclaw:IEEE,2010:1-6.
[12]Shanker T B,Nagamani H N,Punekar G S.Thermal Effects on Acoustic Emission Based PD in Transformer Oil:A study[C]//2012 IEEE 10th International Conference on the Properties and Applications of Dielectric Materials.Bangalore:IEEE,2012:1-4.
[13]Ashraf S A,Stewart B G,Chen gke Zhou,et al.Numerical Simulation of Partial Discharge Acoustic Signals[C]//2008 International Conference on High Voltage Engineering and Application.Chongqing:IEEE,2008:577-579.
[14]Varlow B R,Auckland D W,Smith C D,et al.Acoustic Emission Analysis of High Voltage Insulation[J].IEE Proceedings-Science, Measurement and Technology,1999,146(5):260-263.
[15]Ozaki R,Akumu A O,Ihori H,et al.Simulation of Ultrasonic Wave Propagation of Partial Discharge in Transformer Model[C]//Proceedings of 2001 International Symposium on Electrical Insulating Materials.Himeji:IEEE,2001:880-883.
[16]PETER M.ELEFTHERION.Partial Discharge XXI:A-coustic Emission-Based PD Source Location in Transformers[J].IEEE Electrical Insulation Magazine,1995,11(6):22-26.
[17]Lundgaard L E.Partial Discharge-Part XIII:Acoustic Partial Discharge Detection-Fundamental Considerations[J].IEEE Electrical Insulation Magazine,1992,8(4):25-31.
[18]Howells E,Norton E T.Location of Partial Discharge Sites in On-Line Transformers[J].IEEE Transactions on Power Apparatus and Systems,1981,PAS-100(1):158-162.
[19]卢毅,楼樟达,王大忠.用模式识别法进行油中放电超声定位的研究[J].电工技术学报,1996,14(3):51-53.
[20]律方成,程述一,李燕青,等.超声法在电力变压器局部放电检测中的应用与展望[J].变压器,2012,49(8):45-49.
[21]项琼,伍志荣,聂德鑫,等.电力变压器中的局部放电超声定位技术[C]//2001北京输配电技术国际会议论文集.北京:中国电力企业联合会,2001:551-557.
[22]胡平,林介东,马庆增.声发射技术在变压器局部放电测量中的应用[J].无损检测,2004,26(10):502-505.
[23]孙才新,罗兵,顾乐观,等.变压器局部放电源的电-声和声-声定位法及其评判的研究[J].电工技术学报,1997,12(5):49-52.
[24]Kundu P,Kishore N K,Sinha A K.A Non-Iterative Partial Discharge Source Location Method for Transformer Employing Acoustic Emission Techniques[J].Applied A-coustics,2009,(70):1378-1383.
[25]Linhai Zhang,Gang Liu,Cheng Li,et al.Study on Location of Acoustic Emission Partial Discharge Detection in Power Transformers[C]//2007 International Conference on Solid Dielectrics.Winchester:IEEE,2007:589-592.
[26]Lima S E U,Frazãoa O,Fariasb R G,et al.Acoustic Source Location of Partial Discharges in Transformers[C]//Fourth European Workshop on Optical Sensors.Porto:SPIE,2010:76532N-1-76532N-4.
[27]马立新,陶鹏举.局部放电超声波定位智能算法的研究[J].无线通信技术,2013,(1):41-45.
[28]Xin He,Guangzhong Xie,Yadong Jiang.Online Partial Discharge Detection and Location System Using Wireless Sensor Network[C]//ICSGCE 2011.Chengdu:Elsevier,2011:420-428.
[29]李一峰,姜勇,王红星,等.基于遗传算法的变压器局部放电超声定位法[J].江苏机电工程,2000,19(4):24-26.
[30]律方成,王勇,陈志业,等.大型电力变压器局部放电超声定位的线性算法[J].华北电力学院学报,1993,(3):1-6.
[31]徐银凤,罗日成,易生,等.带混沌搜索的PSO算法在变压器局部放电定位中的应用[J].电力科学与技术学报,2010,25(1):97-100.
[32]毛晋生,王保保,杨晓,等.变压器局部放电检测超声定位方法[C]//2007年全国输变电设备状态检修技术交流研讨会论文集.海口:中国电力企业联合会,2007:211-216.
[33]杨扬,王保保.变压器局部放电超声定位中的自适应优化算法[J].测控技术,2007,(3):100-104.
[34]秦文明.500kV变压器局部放电定位测量[J].高电压技术,1990,(1):52-56.
[35]唐良,李焕章,伍志荣.变压器局部放电超声波定位原理[J].高电压技术,1991(1):39-42.
[36]程述一,律方成,谢庆,等.基于暂态对地电压和超声阵列信号的变压器局放定位方法[J].电工技术学报,2012,27(4):255-262.
