基于摄动原理的火箭弹落点实时预测

李超旺,高敏,宋卫东

(1.军械工程学院导弹工程系,河北石家庄 050003;2.军械工程学院火炮工程系,河北石家庄 050003)

基于摄动原理的火箭弹落点实时预测

李超旺1,高敏1,宋卫东2

(1.军械工程学院导弹工程系,河北石家庄 050003;2.军械工程学院火炮工程系,河北石家庄 050003)

基于摄动原理,提出了以6自由度弹道方程解算的弹道为火箭弹基准弹道,求解参数扰动引起的落点偏差变化量的落点实时预测方法,并给出了详细解算步骤。将各种扰动系数的解算赋予地面火控计算机,降低了弹载计算机的解算复杂度和解算量。以122 mm火箭弹为例,选取一条基准弹道,分别对无扰动、仅存在初始扰动和全弹道存在随机扰动3种条件下的无控弹道进行了落点预测仿真实验和火箭弹落点预测飞行试验。研究结果表明:该方法在仿真实验和实际飞行试验中都具有较高的预测精度,横向偏差收敛速度较纵向偏差快,其波动幅度在全弹道上较纵向偏差小,而且纵向偏差预测在火箭弹降弧段才趋于收敛;采用该方法进行预测时每次解算时间为167 ns左右,远小于弹载控制器2 ms的控制周期,实现了实时预测。

兵器科学与技术;火箭弹;弹道修正弹;落点实时预测;摄动原理;弹道仿真实验

0 引言

弹道修正弹修正能力有限,采用合适的导引方法能使其有限的修正能力得到有效的利用。研究表明采用落点预测导引方法对修正弹进行修正、控制是较合适的选择[1-2]。

落点预测方法主要分为线性拟合和弹道积分外推这两类[3]。张成提出了通过建立弹道参数和落点偏差之间的线性方程来进行落点预测的线性拟合方法[4]。线性拟合方法具有输入参量少,解算速度快的优点,但解算精度不高。Ghosh等[5]和曹营军等[6]提出了采用神经网络算法的落点预测方法,属于线性拟合的一种改进。离线训练的神经网络对于固定条件下的弹道具有较高的精度,但使用范围受限。Kramer提出了通过在线训练弹道模型的方法来进行落点预测的神经网络算法[7],对于无控弹道具有较高的精度,当对弹道进行控制、修正时,在线训练确立的模型不再能反映实际弹道情况,仍采用该方法将会大大降低预测精度,此外,神经网络在线训练所需数据量较大,对于计算机的运算性能要求较高,只适用于地面计算机。

弹道积分外推是以建立的弹道模型为基础,最典型的是建立弹体的6自由度弹道模型,该方法存在解算耗时长的问题,以某型火箭弹射程30 km外推为例,利用2.60 GHz的处理器以10 ms的解算步长在弹道顶点处外推预测一次需要2～3 s的时间,这显然不能满足实时预测的要求。对此很多学者研究了6自由度弹道模型的线性化或简化处理方法,但仍没有解决好预测精度和解算速度的匹配问题[3,8]。

本文提出了一种基于摄动原理的实时落点预测方法。该方法以基准弹道为参考,通过建立弹道参数偏差与落点偏差之间的关系进行落点预测。文中首先建立了弹道修正火箭弹的弹道模型,通过受力分析建立了弹道解算方程。然后提出了基于摄动原理的预测方法,介绍了预测方法的计算步骤,最后以某型火箭弹为例进行了不同条件下的预测仿真实验,并给出了相应的结果。

1 弹道修正火箭弹弹道方程

火箭弹飞行过程中受力情况较为复杂,除受重力、发动机的推力和阻力、升力外,还受燃气流产生的科氏力、尾翼导转力和马格努斯力的影响,为了描述修正弹在飞行过程中的运动特点及弹道情况,本文建立了弹体的6自由度弹道模型。弹体的受力情况与坐标系之间的关系如图1所示。

图1 弹体的受力分布及坐标系图Fig.1 The force around projectile and the coordinate system

如图1(a)所示,Oxyz为发射坐标系,O点为发射点,Ox轴沿发射方向,射程增加方向为正,Oy轴铅直向上,Oz轴满足右手定则。O1x1y1z1为弹体系,与火箭固联,随弹体姿态的改变而改变。其中O1点为弹体质心,O1x1轴沿弹体纵对称轴。为了分析方便,建立了准弹体坐标系O4x4y4z4,如图1(b)所示,其中O4点为弹体质心,与O1点重合,准弹体坐标系相对于弹体是不动的,与弹体坐标系的只有一个滚转角的差别,如图1(c)所示。为了解算方便,在发射系内建立了火箭弹的弹道方程。

发射系内质心运动的运动学方程为

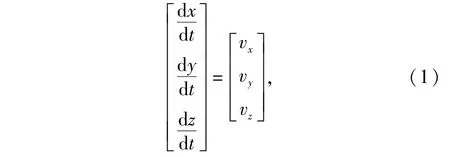
式中:x、y、z为质心在发射坐标系上的分量;vx、vy、vz为飞行速度在发射坐标系上的分量。

发射坐标系内质心运动的动力学方程为

式中:Fx、Fy、Fz为发动机推力在发射坐标系上的分量;Frkx、Frky、Frkz为燃气流动的科氏惯性力在发射坐标系上的分量;Fcx、Fcy、Fcz为推冲器推力在发射坐标系上的分量;Rx、Ry、Rz为空气动力在发射坐标系上的分量;gx、gy、gz为引力加速度在发射坐标系上的分量;acx、acy、acz为科式加速度在发射坐标系上的分量;aex、aey、aez为牵连加速度在发射坐标系上的分量。火箭弹无控飞行时Fc值为0.

准弹体坐标系内绕质心转动的动力学方程为

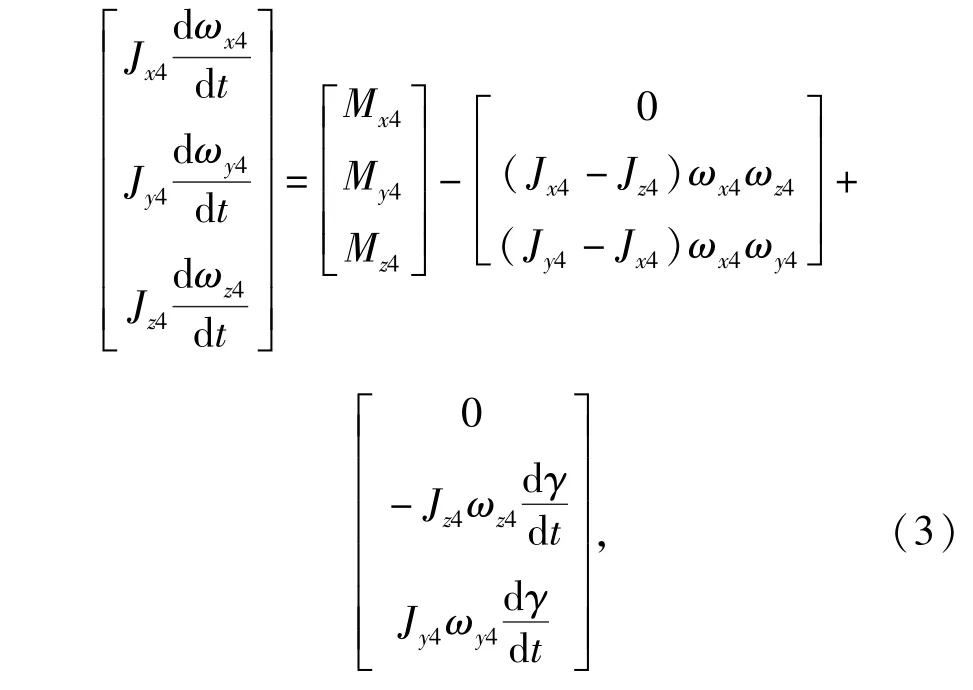
式中:Jx4、Jy4、Jz4为转动惯量在准弹体坐标系上的分量;ωx4、ωy4、ωz4为弹体坐标系相对地面坐标系的转动角速度在准弹体坐标系上的分量;Mx4、My4、Mz4为气动力矩在准弹体坐标系上的分量;γ为弹体的滚转角。

弹体姿态角速度方程为

式中:φ为弹体俯仰角;ψ为偏航角。

准弹体坐标系到弹体坐标系的转换矩阵为

(1)式～(4)式构成火箭弹的弹道方程,对此弹道方程采用4阶龙格—库塔法进行积分解算。解算过程中利用(5)式实现准弹体坐标系到弹体坐标系的转换,气动系数及气动系数导数以马赫数和攻角为变量通过线性插值获取。

2 摄动落点预测方法

理论上,当已知炮位点、目标点的坐标和气象信息时,按照(1)式～(4)式解算出的射击诸元进行发射的火箭弹将会沿着解算出的基准弹道飞行,直至命中目标。但是,火箭弹实际结构、质量和气象等参数会偏离计算基准弹道的标准条件,造成落点的射程和横向偏差,通常这些量都较小,使实际弹道在基准弹道附近摄动。摄动落点预测就是以弹道参数偏差为输入量,通过建立弹道参数偏差和落点偏差之间的关系来进行落点预测。摄动落点预测算法基本流程如图2所示。

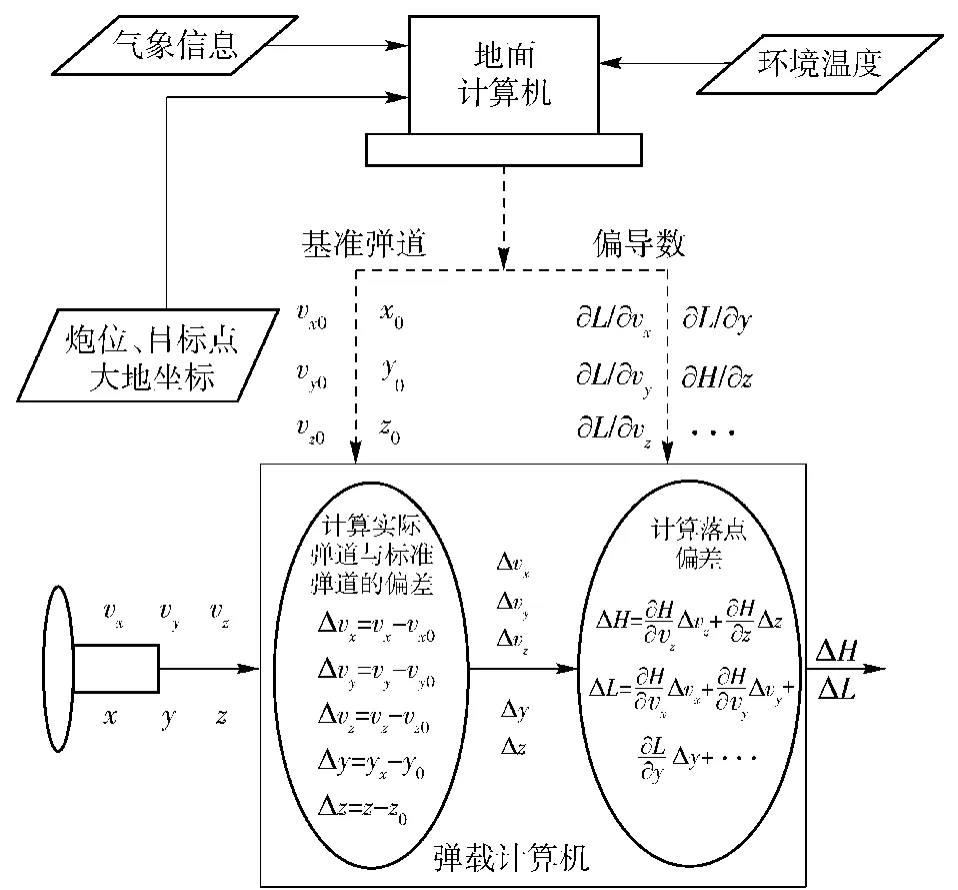
图2 摄动落点预测算法流程图Fig.2 The flow chart of IPP based on perturbation theory

从图2可以看出,摄动落点预测方法整个过程分为地面计算机射前计算和弹载计算机在线解算两部分,地面计算机提供基准弹道和预测偏差系数,弹载计算机根据这些系数及弹体实时的位置、速度信息对落点偏差进行预测。

预测算法流程具体如下:

1)解算基准弹道。给定炮位、目标点坐标、环境温度及气象信息以后解算火炮的射击诸元,确定射击诸元以后计算对应的基准弹道,保存基准弹道内的位置和速度信息。基准弹道的保存间隔越小插值解算时精度会越高,但是减小间隔会导致所需存储的数据量增大,将会更多的占用弹载计算机有限的存储空间,影响弹载计算机的解算速度。因此,基准弹道保存时间间隔值的确定需要综合考虑解算精度要求和弹载处理器运算速度的现实。在不影响弹载计算机运算速度的前提下保存间隔取的越小越好。

2)解算偏导数。由于初始状态误差的存在和气象条件的随机性,实际弹道与基准弹道存在着差别,这种差别反映在同一射程下对应的速度和位置的偏差上,假设射程为x时实际弹道和基准弹道只有一个参量的差别(以vx为例),该点弹道参数vx变化Δvx将会引起射程偏差ΔL,则x点改变单位量的vx引起的落点偏差为ΔL/Δvx,此值为该点vx对应的偏导数,记为∂L/∂vx.采用同样的方法可解算单独改变其他某个或者同时改变多个弹道参数时对应的偏导数。计算偏导数时参数改变组合情况越多越能反映真实情况,预测时精确度会越高,但是相应地会增加计算数据量。以纵向预测为例,当计算值最高取2阶时,两两进行组合需要计算9个偏导数。而当计算值最高取3阶时,根据多项式定理可得所需的偏导数增加到19个,取值间隔不变的情况下,数值量将增加1倍多。将此数据存储到弹载计算机上将会更多地占用有限的内存空间,降低弹载计算机解算性能。同时,计算表明采用3阶及更高阶偏导数对落点进行预测与最高采用2阶偏导数进行落点预测的偏差不大于1 m,对于落点预测精度提高影响不大。基于以上原因,工程应用中最高一般采用2阶偏导数。

3)在线预测偏差。火箭弹出炮口以后,设某一时刻火箭弹在发射坐标系内的纵向、法向和侧向位置、速度分量分别为x、y、z、vx、vy、vz.将纵向位置变量x值赋予基准弹道的射程值,即使得x=x0,插值解算x0射程下对应的基准弹道位置、速度参数,设为y0、z0、vx0、vy0、vz0.插值解算 x=x0射程下各个变量对应的偏导数,设为

对x=x0射程下基准弹道和实际弹道对应的参数进行做差处理。

摄动落点预测方法充分利用了弹道积分外推方法和线性拟合方法各自的特点。从以上步骤可以看出,该方法把弹道循环积分外推这一精度高、耗时长的环节放到了地面计算机上,将地面计算机解算的参数装定到弹载计算机上,飞行过程中弹载计算机只需要对相关参数进行线性插值和算术运算即可实现落点偏差预测。

3 仿真实验及分析

为了验证方法的有效性进行了预测仿真实验及火箭弹飞行试验。仿真实验的目标点是以弹道方程(1)式～(4)式为基础,通过4阶龙格-库塔法进行积分解算的,其中气动系数和气动系数导数以马赫数和攻角为输入量通过线性插值获取。

图3为以45°射角解算的122 mm火箭弹的基准弹道和目标点。图4为射程与横偏的关系图。

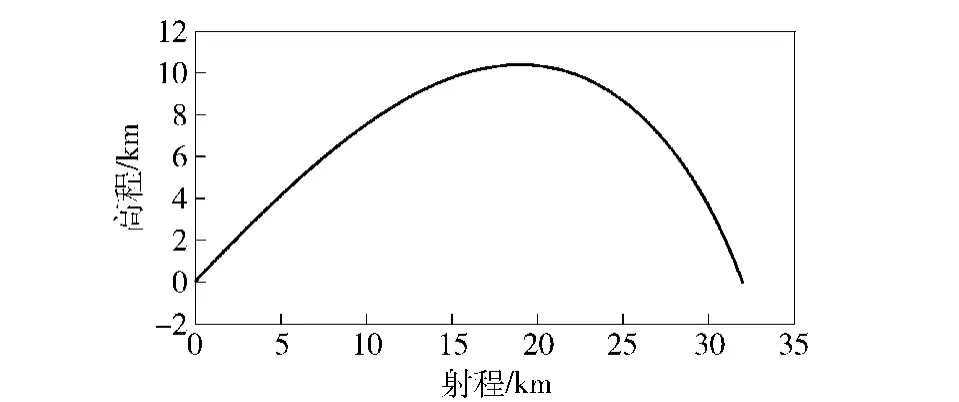
图3 射程-高程对应图Fig.3 Range versus altitude

图3中火箭弹的射程为32 012.5 m,最大高程为10 394.2 m.

图4 射程-横向偏差对应图Fig.4 Range versus cross range

从图4可以看出,受燃气流产生的科氏力的影响,火箭弹出炮口以后飞往射向的右方,发动机关闭以后火箭弹受马格努斯力的影响开始往射向的左侧飞行,直至落地,落地点距发射方向的距离为71 m左右,整条弹道的飞行时间约为94 s.从图3和图4可以确定目标点在发射坐标系内的坐标是(32 012.5 m,71 m)。

仿真实验平台为以美国 TI公司生产的MS320C6713为主处理器的控制器。

实验1:初始状态、气动系数和气象信息无测量误差时落点预测情况。

假设火箭弹发射时弹体的状态和气象条件同测量值,则摄动落点预测方法预测的落点将会与目标点重合,预测仿真实验结果如图5所示。

图5 时间-预测偏差对比图Fig.5 Time versus predictive errors

从图5可以看出,从20 s预测开始到94 s预测结束这一时间段内预测偏差收敛都较快、较准。纵向预测偏差最大为0.02 m左右,横向预测偏差更为准确、平稳,这可能是因为纵向预测偏差涉及的变量较多,线性插值时降低了部分变量的精度。纵向预测偏差有波动,但最大预测偏差只有0.02 m,远小于线性化模型同条件下10 m的预测误差[3]。

实验2:初始状态存在偏差时落点预测情况。

由于加工误差和测量误差的存在,火箭弹总体参数理论值与实际值会存在差别,这种差别将会引起发动机关机时刻弹体的实际速度与理论速度出现偏差。由于加工误差和测量误差是随机的,所以引起的速度偏差大小也是随机的,假设发动机关机时刻某条弹道弹体的纵向速度和侧向速度比理论值分别大了3.6 m/s和1.5 m/s,针对这种情况进行了扰动弹道解算和落点预测仿真。扰动弹道和基准弹道的对比情况如图6所示。

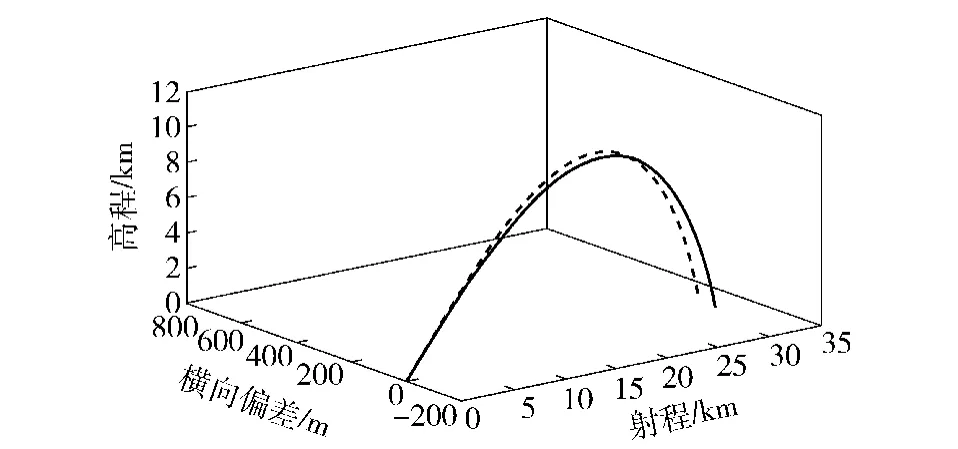
图6 基准弹道与扰动弹道对比图Fig.6 Standard trajectory versus disturbed trajectory

从图6可以看出,受扰动因素的影响火箭弹实际飞行中偏离了基准弹道,直至落地。最终火箭弹在发射坐标系内的落点坐标为(32 121 m,133.2 m)。火箭弹的落点较目标点偏远了108.5 m,偏左62.2 m.弹上横向和纵向预测情况如图7所示。

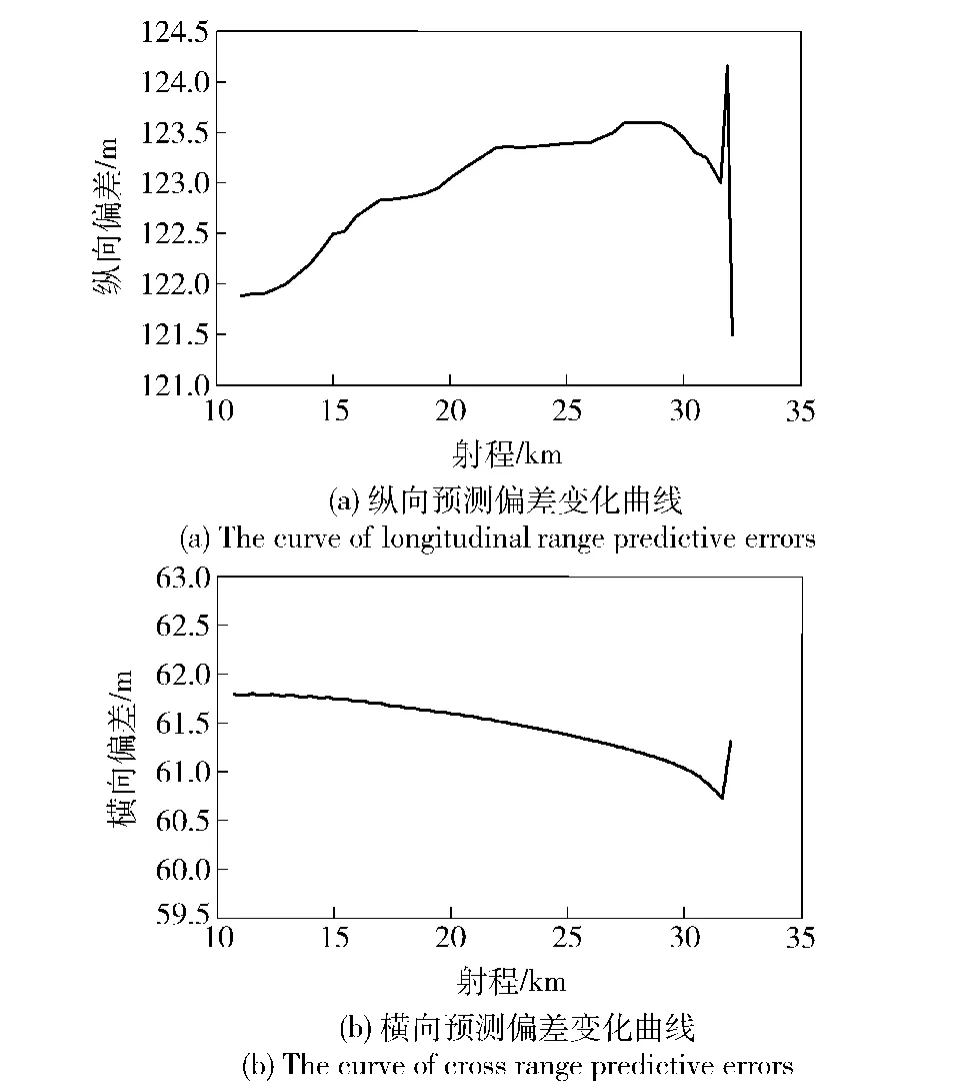
图7 纵向与横向预测偏差变化曲线Fig.7 Comparison of longitudinal and cross range predictive errors

从图7(a)中可以看到,11 km时弹丸的纵向落点预测偏差为121.9 m左右,此后预测偏差逐渐增大。射程28 km时预测偏差达到了最大值约为123.6 m,但与实际落点偏差只差了15.1 m.此后预测落点偏差有收敛的趋势,但在最后100 m射程内预测偏差出现了较大的波动,这是因为实际弹道的射程超出了装定的基准弹道值,进而利用射程进行线性插值求取偏导数时将会出现偏差。从图7(b)可以看出,11 km时弹丸的横向落点预测偏差为61.8 m,此后预测偏差逐渐减小,快落地时落点偏差达到了极小值为 60.8 m,与实际偏差只相差了1.4 m.后面出现了波动,原因同图7(a)。

从以上可以看出,摄动落点预测方法在火箭弹存在初始扰动时仍保持了相当高的精度。可以满足弹道修正弹对落点预测导引的需求。

实验3:初始条件和气动参数、环境条件都存在随机误差时。

当初始条件和气动参数都存在误差时需要通过蒙特卡洛打靶的方法进行验证。采用表1所示误差均值作为输入量,其中每种误差都是服从正态分布的。

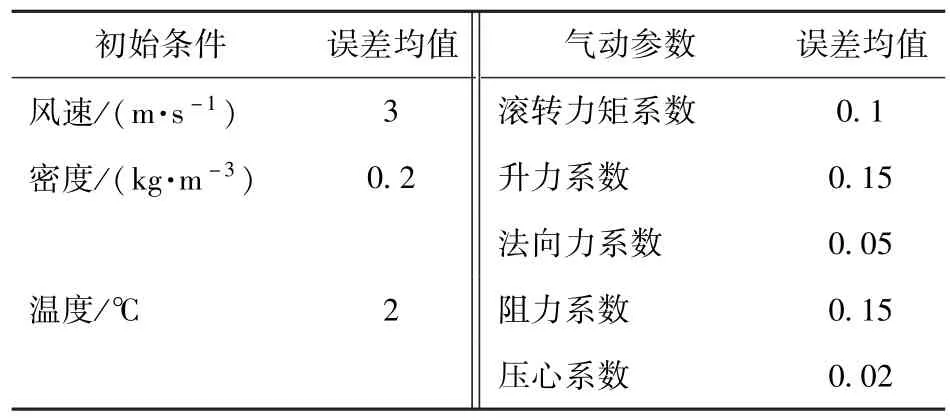
表1 初始条件和气动参数误差均值表Tab.1 Initial terms and dynamic parameter error mean values

预测仿真时系数误差值通过误差均值乘以随机数的形式加入到弹道方程里面,采用这种形式进行了多次仿真实验。为了考察该方法在不同误差下的预测精度,随机选取了其中一条落点偏差较大的弹道来进行情况说明。

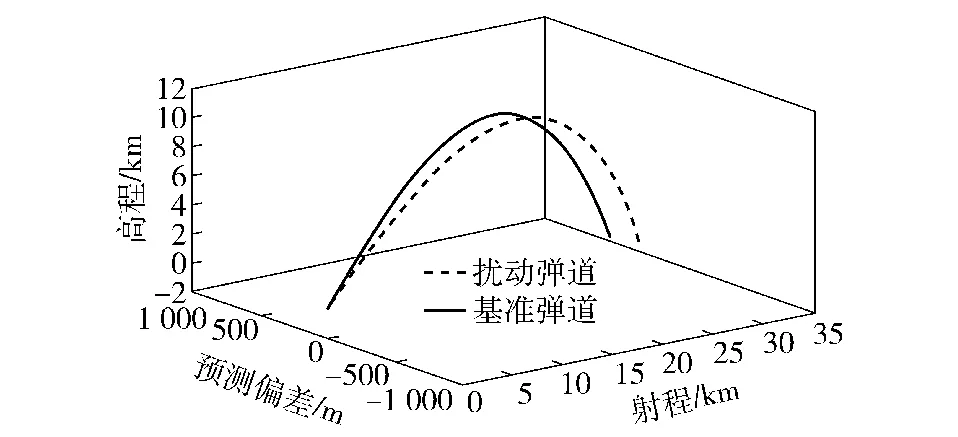
图8 某条全程扰动弹道和基准弹道对比情况Fig.8 Comparison of standard trajectory and disturbed trajectory

从图8可以看出,该条弹道的实际落点在发射坐标系内的坐标为(31 037 m,-151.3 m),相对于目标点偏近了975.5 m,偏右了232.3 m.弹上预测情况如图9所示。

从图9(a)可以看出,火箭弹飞出11 km左右开始进行落点预测,预测的火箭弹射程较目标点近700 m左右,而实际落点为960 m左右,这时的预测误差为260 m,此后预测偏差开始逐渐收敛,18 km时火箭弹飞过了最高点,预测偏差变得较为准确,在960 m左右进行波动,这种状况一直维持到了落地为止。落地时预测的落点坐标为949 m,与实际值偏离了26.5 m,预测误差只有2.72%.

从图9(b)可以看出,弹飞出11 km左右开始预测时预测的横向偏差为227 m左右,与实际落点只差了5.3 m,此后预测偏差值开始逐渐减小,落地时预测偏差为218 m,与实际横向偏差值差14.3 m.这可能是由于落点差值太大,导致插值时偏导数不准。

从以上分析可以看出,当实际弹道落点偏离基准弹道约1 000 m时该方法仍能保持较高的预测精度。

试验4:无控火箭弹飞行试验。

为了验证方法的精度和解算实时性,进行了火箭弹的落点预测飞行试验。试验中所用参数按照第2节介绍的方法进行解算,为了降低不确定因素造成的方法误差,利用贝尔雷达取代卫星接收机对火箭弹进行弹道参数测量,火箭弹实际飞行轨迹及预测偏差具体情况如图10所示。

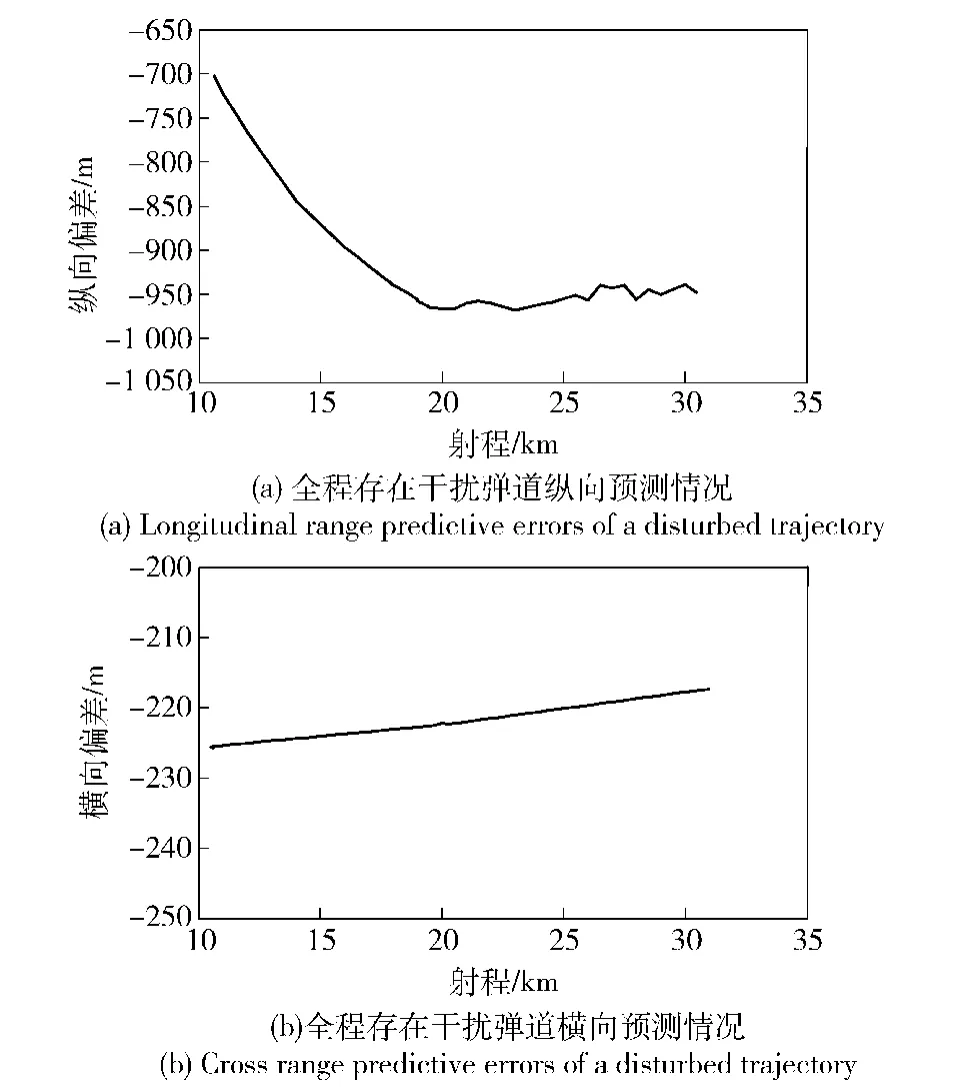
图9 全程存在干扰弹道偏差预测情况Fig.9 Comparison of predictive errors for a disturbed trajectory

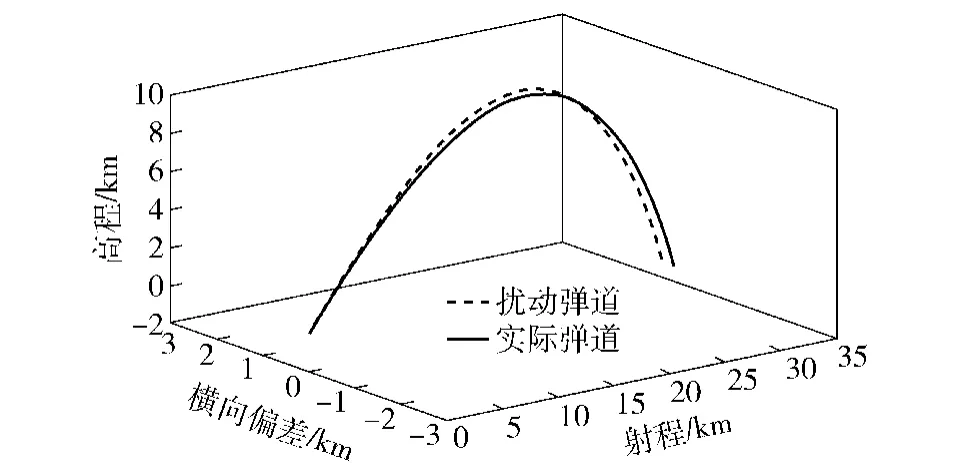
图10 无控火箭弹实际弹道和基准弹道对比情况Fig.10 Comparison of a real trajectory and standard trajectory

从图10可以看出,基准弹道落点即目标点坐标为(33 590 m,514.9 m),而靶场提供的雷达测量数据显示火箭弹实际落点坐标为(33 349 m,-587.9 m)。实际落点较目标点偏近241 m,偏左1 102.8 m.弹上预测情况如图11所示。

图11 无控火箭弹飞行试验预测偏差情况Fig.11 The IPP value of a flight test

从图11可以看出,火箭弹飞出10 km左右横向预测偏差为1 002 m,而靶场提供的落点实际偏差为1 102.8 m,这时的预测偏差为100.8 m,此后预测偏差开始逐渐收敛。射程为23 600 m时,纵向预测偏差为1 114 m,与实际落点相差11.2 m,此后弹道预测偏差有波动,但是都维持在1 110～1 120 m之间,弹道预测偏差与实际落点偏差为7.2～17.2 m.

从图11还可以看出,火箭弹飞出10 km左右纵向预测偏差为99.2 m,而靶场提供的落点实际偏差为241 m,这时的预测偏差为141.7 m,此后预测偏差开始逐渐收敛。射程为23 600 m时,纵向预测偏差为240.3 m,与实际落点相差0.7 m,火箭弹落地时纵向预测偏差为220 m,与实际落点相差了21 m.

3次仿真实验及1次实际飞行试验结果表明,采用摄动方法预测时横向偏差收敛速度较纵向偏差快,横向预测偏差波动相对小。在不同的干扰条件下摄动落点预测方法都具有较高的预测精度,可用于弹道修正弹的控制、修正。此外,摄动落点预测算法简化了计算量,采用该方法每次进行落点预测时弹载计算机只需进行二次线性插值、一次做差运算和一次相乘运算,不存在积分等迭代运算,相当于每次预测解算只需执行4条指令,而TMS320C6713数字处理器工作周期为5 ns,处理速度高达2 400 MIPS,则每次解算时间为167 ns,远小于控制器的控制周期2 ms,能满足实时性要求。

4 结论

在建立6自由度弹道模型的基础上,提出了基于摄动原理的实时落点预测方法,只需要获得火箭弹飞行中的位置和速度信息就可快速预测出落点和目标点的偏差。该算法的流程、步骤表明,落点实时解算所需的输入量少,降低了弹载计算机的运算量,提高了解算速度。基于该方法进行了122 mm火箭弹3种典型条件下的落点预测仿真实验及无控飞行试验,仿真结果表明落点纵向偏差近1 000 m时,预测误差为26.5 m,飞行试验数据表明这一误差为21 m.仿真实验横向预测误差为5.3～14.3 m,而飞行试验预测误差范围为7.2～17.2 m.飞行试验结果与仿真实验结果具有较高的一致性。采用该方法简化了弹载计算机的运算量,在典型仿真平台上,解算时间在200 ns以内,远小于弹载控制器2 ms的控制周期,该方法能够满足火箭弹在线实时预测要求,可用于火箭弹的落点预测及飞行控制。

References)

[1] Burchett B,Costello M.Model predictive lateral pulse jet control of an atmospheric rocket[J].Journal of Guidance,Control,and Dynamic,2002,25(5):860-867.

[2] Hahn P V,Frederick R A,Slegers N.Predictive guidance of a projectile for hit-to-kill interception[J].IEEE Transactions on Control Systems Technology,2009,17(4):745-755.

[3] Fresconi F,Cooper G,Costello M.Practical assessment of realtime impact point estimators for smart weapons[J].Journal of Aerospace Engineering,2010,24(1):1-11.

[4] 张成.脉冲修正弹药射程预测控制方法[J].弹道学报, 2010,22(1):20-23.

ZHANG Cheng.Range prediction control method for pulse jet correction projectiles[J].Journal of Ballistics,2010,22(1):20-23.(in Chinese)

[5] Ghosh A K,Prakash O.Neural models for predicting trajectory performance of an artillery rocket[J].Journal of Aerospace Computing,Information,and Communication,2004,1(2):112-115.

[6] 曹营军,朱宗平,李立春,等.基于BP人工神经网络的末修弹落点预测导引模式[J].弹箭与制导学报,2011,31(6): 76-78.

CAO Ying-jun,ZHU Zong-ping,LI li-chun.Impact point prediction guidance mode of terminal trajectory correction projectile based on BP artificial neural networks[J].Journal of Projectile,Rockets,Missile and Guidance,2011,31(6):76-78.(in Chinese)

[7] Kramer K A.Impact time and point predicted using a neural extended Kalman filter[C]//The 2005 International Conference on Intelligent Sensors,Sensor Networks and Information Processing Conference.Melbourne,Australia:IEEE,2005:199-204.

[8] Ravindra V C,Bar-Shalom Y,Willett P.Projectile identification and impact point prediction[J].IEEE Transactions on Aerospace and Electronic Systems,2010,46(4):2004-2021.

Real-time Impact Point Prediction of Rocket Projectile Based on Perturbation Theory

LI Chao-wang1,GAO Min1,SONG Wei-dong2
(1.Missile Engineering Department,Ordnance Engineering College,Shijiazhuang 050003,Hebei,China; 2.Artillery Engineering Department,Ordnance Engineering College,Shijiazhuang 050003,Hebei,China)

The 6-degrees of freedom trajectory equations for rocket projectiles are established,and a new real-time impact point prediction(IPP)approach is proposed based on perturbation theory.Assuming that the rocket projectile flies along the nominal trajectory without disturbance,the detailed calculation process of the dispersion in impact point is presented.The prediction coefficient is calculated using a fire control computer on the ground,and IPP is carried out using the rocket-borne computer during flight.As a result,the IPP process is simplified.Finally,the simulation and flight tests of 122 mm rockets is accomplished.The results show that its prediction precision is higher under any condition.At the same time,the results demonstrate that the time consumed to predict the impact point is about 167 ns,which is much less than the control cycle time of 2 ms.

ordnance science and technology;rocket projectile;trajectory correction munition;real-time impact point prediction;perturbation theory;trajectory simulation experiment

TJ012

:A

:1000-1093(2014)08-1164-08

10.3969/j.issn.1000-1093.2014.08.005

2013-07-22

李超旺(1985—),男,博士研究生。E-mail:lichaowangzxz@163.com;高敏(1963—),男,教授,博士生导师。E-mail:gaomin1106@gmail.com