基于支持向量机回归的宁夏地震前兆综合预测模型研究*

2014-07-05卫定军罗国富司学芸李国斌

地震研究 2014年2期

卫定军，罗国富，司学芸，李国斌，李英

(宁夏回族自治区地震局，宁夏银川750001)

0 引言

宁夏位于南北地震带北段，地质构造复杂，境内存在一系列规模较大的活动断裂(杨明芝等，2007)。历史上曾发生多次强烈地震，如1739年银川—平罗8级地震和1920年海原8.5级地震。近年来，随着地震监测台网的建设，监测资料日益丰富，各种地震前兆异常越来越多，这些异常与未来地震的关系如何，成为分析预报人员研究的重点。前兆异常与地震之间的关系具有较强的不确定性和不可重复性，一些异常出现后，并不一定发生较强地震。因此，地震前兆异常与未来地震之间具有较强的非线性关系，很难通过某种解析表达式进行表达。这就需要综合考量各种地震前兆异常信息，运用统计学、物理学和系统学的方法进行地震前兆综合预测，以此来判断地震前兆异常与未来地震之间的关系(梅世蓉等，1993)。

近年来，一种具有高度自适应能力的非线性动力系统——支持向量机被引入地震综合预测研究中，该方法适用于小样本事件，能够很好地建立起输入与输出之间的非线性不确定复杂关系。王炜等(2005，2006a，b)首先使用该方法，对我国大陆强震活动的时间序列与全球的强震活动、太阳黑子活动之间的关系等进行了研究;蒋淳等(2006)使用该方法在地震综合预测方面进行了有益的探索;李志雄等(2007a，b)应用该方法对中国西南地区、华北地区年度地震活动强度进行了预测;武安绪等(2008)利用该方法和中国大陆中强地震前兆异常建立了中国大陆中强地震前兆综合预测模型，该模型的内符检验预测结果与实际震例的地震震级基本一致，取得了良好的应用效果。本文在总结20世纪70年代以来宁夏及周边地区发生的一系列中强地震震例资料的基础上，运用支持向量机回归算法，以宁夏及邻区实际发生的震例为样本，建立起适用于宁夏及邻区的各类地震前兆异常与地震震级之间的非线性映射关系，形成地震前兆综合预测模型，研究宁夏及邻区地震前兆异常与地震震级之间的关系，以期在宁夏及周边地区未来震情研判中发挥作用。

1 基本理论

支持向量机(SupportVectorMachines，SVM)是由Vapnik于1995年在统计学理论的基础上首次提出的一种新学习算法(Vladimir，2000)，它建立在统计学习理论的VC维理论和结构风险最小原理的基础上，根据有限的样本信息在模型的复杂性(即对特定训练样本的学习精度)和学习能力(即无错误地识别任意样本的能力)之间寻求最佳折衷，以求获得最好的推广能力。支持向量机的基本思想是基于Mercer核展开定理，通过非线性映射φ把样本空间映射到一个高维乃至于无穷维的特征空间(Hilbert空间)，使得在特征空间中可以应用线性学习机的方法解决样本空间中的高度非线性等问题(Nello，John，2004)。

设样本为(x1，y1)，…，(xk，yk)∈Rn× R的k维向量，待拟合函数为f(x)=w·φ(x)+b。支持向量机通过在约束条件yi－(w·φ(xi)+b)≤ε+ξi下极小化函数

来确定回归函数。式(1)中第1项是使回归函数更为平坦，从而提高泛化能力，第2项则为减少误差，常数C＞0控制对超出误差ε的样本的惩罚程度。ξ和ξ*是松弛因子。ε是大于零的常数，f(xi)与yi的差小于ε时不计入误差，大于ε时误差计为对于非线性拟合，首先通过非线性变换φ(x)将输入空间映射成高维的特征空间，然后在高维的特征空间中进行线性逼近，从而取得在原空间非线性回归的效果。此时待求拟合函数可表示为

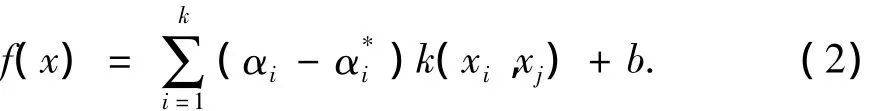
其中:αi、为拉格朗日乘子，且(αi－)不为零，k(xi，xj)=φ(xi)·φ(xj)。支持向量机理论只考虑高维特征空间的点积运算k(xi，xj)=φ(xi)·φ(xj)，而不直接使用函数φ，从而巧妙地解决了因φ未知w而无法表达的问题，称k(xi，xj)为核函数。已经证明，只要满足Mercer条件的对称函数即可作为核函数，常用的核函数有

(1)多项式核函数 k(xi，xj)=(xi·xj+c)d，c＞ 0，d=1，2，…;

(2)径向基(RBF)核函数 k(xi，xj)=exp

(3)Sigmoid 核函数 k(xi，xj)=tanh［b(xi·xj)+c］;

其中RBF核函数因其优秀的局部逼近特性在SVM中应用最为广泛。利用现有的优化软件包可以很容易的实现上述算法。

2 支持向量机在宁夏地震前兆综合预测中的应用

20世纪70年代以来宁夏及邻区发生20多次5级以上地震，积累了较丰富的中强地震资料，这些地震发生前均出现过一定数量的前兆异常，充分利用这些资料对今后的地震预测工作具有重要的参考价值。在地震预报三要素中，震级的预测是重要的预测量之一，地震前兆异常的持续时间和种类与未来地震震级存在一定关系。本文的基本思路为在总结宁夏及邻区中强地震震例资料的基础上，应用支持向量机方法，探索宁夏及邻区地震前兆异常的异常时段与中强地震震级之间的关系，形成多种地震前兆组合的综合预测模型，为未来宁夏及邻区震情判断提供判据。

2.1 中强地震前兆异常资料

本文以中国震例(张肇诚等，1988，1990a，b，1999，2000;陈棋福等，2002，2003)和宁夏及邻区中强以上地震预测指标和震后趋势判断①宁夏回族自治区地震局.2007.宁夏及邻区中强以上地震预测指标和震后趋势判断.的研究成果为基础，对1970年以来宁夏及邻区发生的中强地震进行了总结，系统整理了这些地震前宁夏存在的地震前兆异常项目(表1)。由表1可以看出，多数地震都出现过测震学和前兆观测异常，只有1970年12月3日宁夏西吉5.5级、1971年6月28日宁夏吴忠5.1级地震前仅存在测震学异常，其原因为该段时间宁夏境内前兆观测手段偏少。对于宁夏邻区发生的中强地震，有部分地震前仅出现过前兆观测异常，如1984年1月6日甘肃武威5.3级、1987年1月8日甘肃迭部5.9级和1995年7月22日甘肃永登5.8级地震。需要指出的是，1988年1月4日宁夏灵武5.5级地震和1988年1月10日宁夏灵武5.0级地震前后仅隔6天，在整理时将它们作为一次地震事件。1998年7月29日海原4.9级地震前，宁夏存在多项测震学及前兆观测异常，也将其进行了统计(研究时段期间宁夏境内仅发生过这一次4.9级地震)。

表1 1970年以来宁夏及邻区中强地震及震前宁夏存在的异常项目Tab.1 The moderate and strong earthquakes occurred in Ningxia and its adjacent areas since 1970 and precursory anomalies of Ningxia before these earthquakes

2.2 样本数据集的构建

本文主要研究宁夏地震前兆异常量与可能发生的地震震级之间的关系，而影响震级的因素有很多种。在表1中震例总结的基础上，统计了在各次震例中出现次数相对较多的异常项目，并借鉴王炜等(1999)的研究，选择了地震条带、地震空区、应变释放、地震频次、b值、地震学参数、短水准、地倾斜、地电、水化学、水位、重力、地磁13个异常项目作为主要影响震级的因素量。需要说明的是，本文将η值、b值、Mf值、D值、GL值、Rm值等测震学参数统一归类为地震学参数，而将水氡、气氡、CO2、He、Cl－、CH4等地下水化学参量统一归类为水化学。

从表1整理的23个震例中筛选了21个，1984年1月6日甘肃武威5.4级和1987年1月8日甘肃迭部5.9级地震宁夏境内仅各出现一项地震前兆异常，异常数量偏少，故而剔除这2次震例。对筛选的21个震例统计上述13项异常项目的持续时间，将其作为SVM的输入参数，实发震级作为输出参数，从而构成SVM的样本集。对于前兆观测项目，一次地震前可能多个台站出现异常，因此在统计异常持续时间时，当某项前兆观测异常有多台出现，取其加权和为输入值，即某台站某项前兆观测异常的持续时间与相应的权系数相乘，然后将所有台项求和。权系数为某台站某项前兆观测异常的持续时间在所有该项前兆观测异常的持续时间中所占的比例。采用同样方法对地震学参数和水化学这两个综合的异常指标进行处理。由于每个震例出现的异常项目并不相同，因此对于某一震例如果没有对应的异常项目，则该项目的异常持续时间统计为0。结果如表2所示，其中地震序号同表1中地震序号一致。

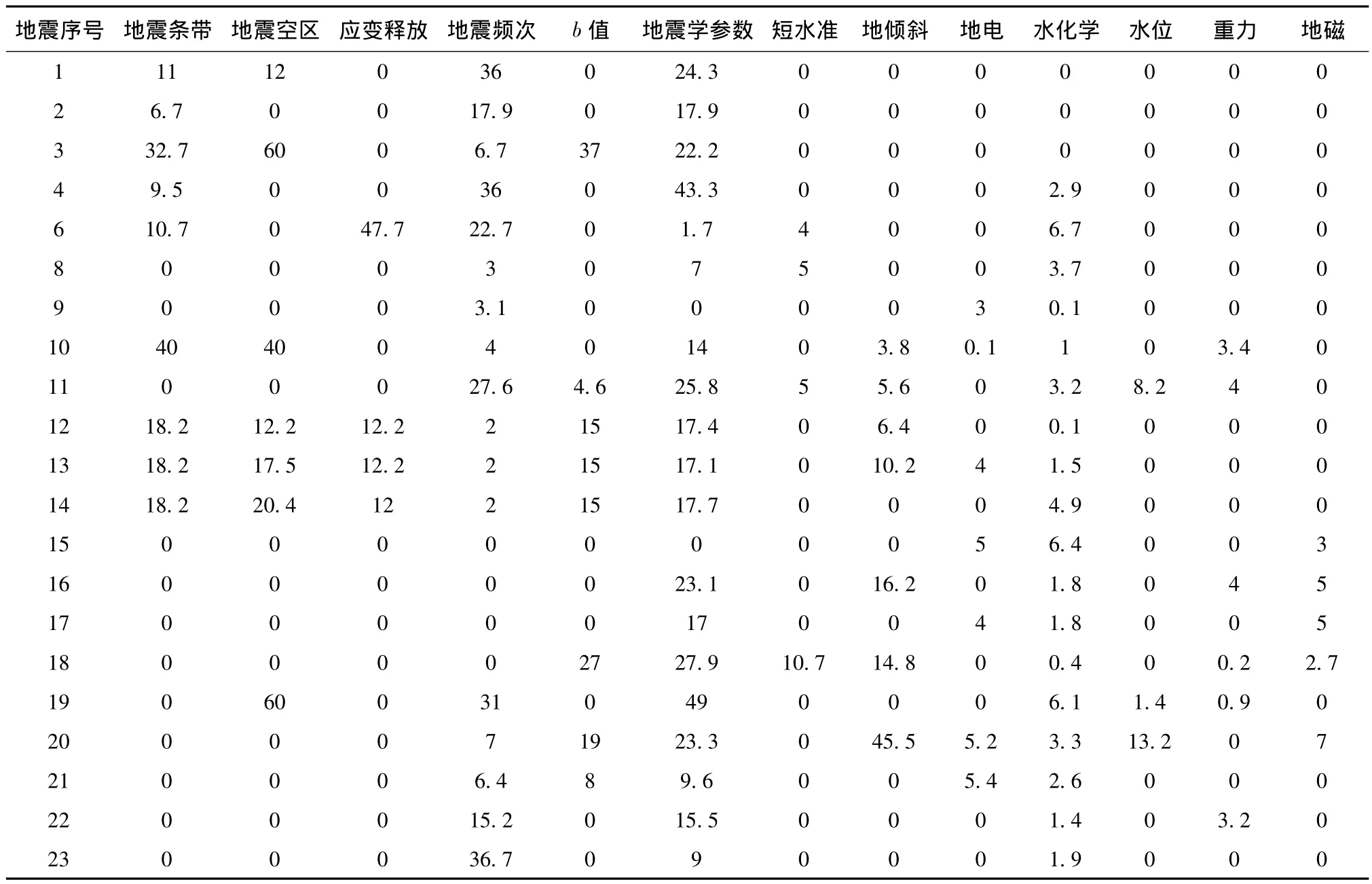
表2 宁夏及邻区中强地震震例异常持续时间统计(单位:月)Tab.2 Duration statistics of anomalies before the moderate and strong earthquakes in Ningxia and its adjacent areas(Unit:Month)

2.3 支持向量机地震前兆综合预测模型的建立

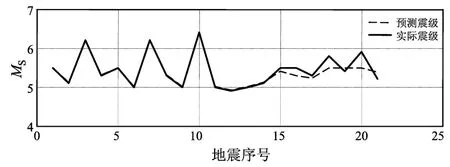
图学习和测试样本的回归预测结果Fig.1 Predicted results of learning and test sample

在样本集确定之后，地震前兆综合预测模型的建立主要依赖于相应的支持向量机核函数和常数C的选择，它们对预测结果的影响很大，它们的合理确定直接影响模型的精度和推广能力(赵洪波，冯夏庭，2003)。本文通过对各种核函数的测试，最终选定径向基RBF函数为核函数。对于核函数参数σ和常数C的选取，考虑到人工搜索存在很大的盲目性，不能保证找到的参数是最优参数，本文采用遗传算法进行参数寻优，最终确定了所用模型的参数，分别为σ=0.6，C=2.1，ε=0.01。对于表2中筛选的21个震例样本，选择其中地震序号为 1～3、6、8、10、11、13、14、16、18、19、22、23共14个震例作为学习样本，其余地震序号为4、9、12、15、17、20、21的7个震例作为外推预测样本，通过得到的模型计算各个震例的预测值，结果见图1。在选择学习样本时充分考虑了各个震例的输入属性及输出震级的全面性，使得预测模型进行充分的学习。

由图1可得，若以震级误差±0.5为限，14个学习内检震例样本的预测震级均在误差范围内，准确率达到了100%;而7个外推预测震例震级样本的预测震级也均在误差范围内，其中最大的预测震级误差为0.4，最小的预测震级误差为0.1，外推预测的准确率也达到了100%。由此可见，该综合预测模型具有较强的学习能力，且具有一定的外推泛化能力，可以在实际的地震预测中发挥一定作用。

支持向量机核函数参数σ和常数C的选择是否合理，将直接影响模型的精度和推广能力，本文在选取最优参数时使用了遗传算法，该方法能够避免人工选择的盲目性。为了检验遗传算法的参数寻优效果，本文使用与武安绪等(2008)相同的资料以及相同的学习样本和检验样本，选用遗传算法找到的参数进行支持向量机回归预测，获得了与武安绪等(2008)研究成果相近的结果(图2)。因此，使用遗传算法进行参数寻优在参数选择时是可行的。

图2 中国震例样本的预测结果Fig.2 Predicted results of earthquake sample in China

3 结论与讨论

本文旨在将支持向量机方法应用于宁夏及邻区的地震综合预测研究中，通过建立基于多种地震前兆异常的地震综合预测模型，初步研究了支持向量机方法在宁夏地震综合预测中的应用情况，研究结果表明利用支持向量机形成的地震综合预测模型对宁夏及邻区可能发生的地震震级具有一定的预测能力。例如，2011年利用该模型预测宁夏及邻区未来可能发生5.3级左右的地震，2012年11月20日宁夏永宁发生了4.5级地震，震级差为0.8级。尽管与预测震级有一定的差距，但是仍然可以看出该模型具有一定的预测能力，而且该地震发生后，许多异常仍在持续发展，可能预示着未来有更大震级的地震发生。

据不完全统计，目前我国用于地震预测预报的测震学参数有几十种，前兆观测有水化、水位、地电、地磁、电磁波、形变、重力、应力等多项指标。如何从各种地震活动参数和前兆手段中选择出适合于某一区域的预测指标在实际地震预测研究中具有重要意义。本文通过震例总结和支持向量机地震综合预测模型研究表明，地震条带、地震空区、应变释放、地震频次、b值、地震学参数，短水准、地倾斜、地电、水化学、水位、重力、地磁等测震学和前兆观测异常指标在宁夏地震综合预测中具有一定的使用价值。

陈棋福，郑大林，高荣胜.2003.中国震例(1997－1999)［M］.北京:地震出版社，136－145.

陈棋福，郑大林，刘桂萍，等.2002.中国震例(1995－1996)［M］.北京:地震出版社，146－164.

蒋淳，魏雪丽，陆远忠，等.2006.支持向量机在地震综合预测中的初步应用［J］.中国地震，22(3):303－310.

李志雄，袁锡文，丁军，等.2007a.中国西南地区强震预测的支持向量机方法［J］.地震研究，30(2):134－136.

李志雄，曾钢平，丘学林，等.2007b.预测华北地区年度地震趋势的支持向量机分类方法［J］.华北地震科学，25(3):11－14.

梅世蓉，冯德益，张国民，等.1993.中国地震预报概论［M］.北京:地震出版社，328－427.

王炜，蒋春曦，张军，等.1999.BP神经网络在地震综合预报中的应用［J］.地震，19(2):118－126.

王炜，林命週，马钦忠，等.2006a.支持向量机及其在地震预报中的应用前景［J］.西北地震学报，28(1):78－84.

王炜，刘悦，李国正，等.2005.中国大陆强震时间序列预测的支持向量机方法［J］.地震，25(4):26－32.

王炜，刘悦，李国正，等.2006b.我国大陆强震预测的支持向量机方法［J］.地震学报，28(1):29 －36.

武安绪，张永仙，张晓东，等.2008.地震前兆综合预测支持向量机模型研究［J］.地震，28(3):55－60.

杨明芝，马禾青，廖玉华.2007.宁夏地震活动与研究［M］.北京:地震出版社，1－9.