基于GM（1，1）的济南市餐厨垃圾产生量预测

陈 娟，杨秀禄，张 玥，王富生

（济南市环境卫生科学研究所，山东 济南 250023）

由于济南市餐厨垃圾产生量统计数据稀缺，餐厨垃圾产生系统的不确定性因素非常多，这给传统方法进行产生量预测带来很大困难，通过对国内外餐厨垃圾预测方法及模型进行多方面总结得出：灰色数学模型方法可以解决数据稀缺条件下的某些量的预测问题，为此选用灰色数学模型方法对济南市餐厨垃圾产生量进行预测。GM（1，1）可以利用统计学的计算机模拟语言和软件完成预测，如DPS、SPSS等。本研究选择DPS平台完成济南市餐厨垃圾产生量的灰色预测。

1 餐厨垃圾产生量的计算

按照餐厨垃圾处理技术规范规定的方法计算济南市餐饮垃圾的产生量：

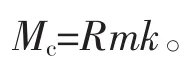
式中：Mc为济南市餐饮垃圾日产生量，kg/d；R为济南市常住人口；m为人均餐饮垃圾产生量基数，kg/（人·d），m 宜取 0.1 kg/（人·d）；k 为餐饮垃圾产生量修正系数。经济发达城市、旅游业发达旅游城市、经济发达沿海城市可取1.15～1.3，济南市属于普通城市可取1.00。

Mc=349.44×104人×0.1 kg/（人·d）×1.00=349 440 kg/d。

则，济南市区餐饮垃圾的日产生量约为350 t/d。

2 预测过程

本研究借用灰色数学模型预测需要的原始数据少且能得到满意结果的特点，对济南市餐厨垃圾进行产生量预测。GM（1，1）预测模型的建立需要遵循以下7个步骤。

第1步：对原始数据序列作一次累加。目的在于为建模提供中间信息，使原始时间序列的随机性加以弱化。

若原始数据序列为X（0）={X（0）（1），X（0）（2），…，X（0）（n）}，累加后生成数列 X（1）={X（1）（1），X1（2），…，X（1）（n）}。其中：

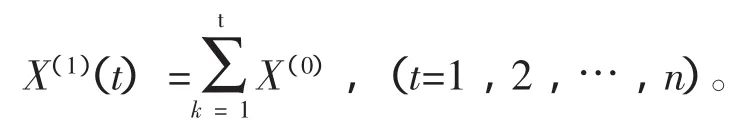
第2步：构造累加矩阵与常数项向量Yn。

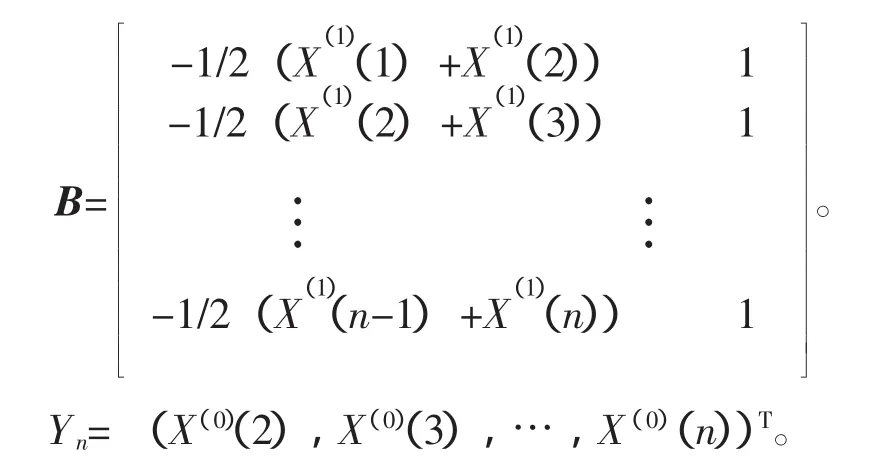
第3步：用最小二乘法解灰参数α。

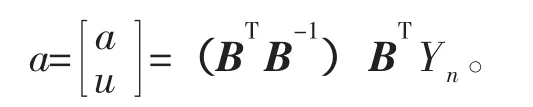
第4步：将灰参数代入时间微分方程。

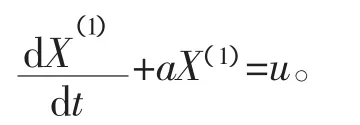
解微分方程得时间函数：

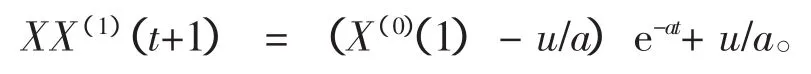
第5步：递减还原。

第6步：精度检验。

常用的检验方法有残差检验、关联度检验及后验差检验等。本研究进行的是验差检验：先计算观察数据离差s1和残差的离差s2，在计算后验比：c=s1/s2。

根据后验比c和小误差概率p对模型进行诊断，当p＞0.95和c＜0.35时，模型可靠，可根据模型对系统行为进行预测。

第7步：若精度达到要求，则可利用所建模型进行预测，建模完成。若精度达不到要求，则还需建立残差修正模型以提高精度，然后利用修改后的模型进行预测。

3 预测结果

根据餐厨垃圾处理技术规范规定，计算得到：济南市餐厨垃圾产生量与人口有直接关系，日产生量是与人口（万人）数值相关，根据此关系预测济南市近远期餐厨垃圾生产量。

对济南市餐厨垃圾日产生量进行一次模拟，得到表1。

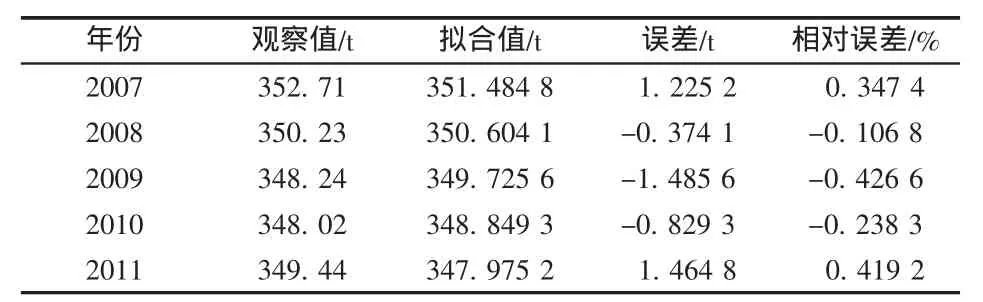
表1 济南市餐厨垃圾产生量GM（1，1）模拟结果

对当前模型的评价：

c=0.635 9，一般；p=0.600 0，不好。

继续对残差序列进行建模分析，得到表2。

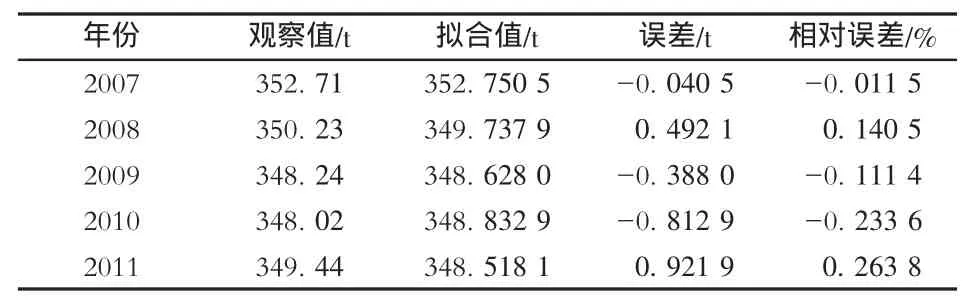
表2 GM（1，1）第1次残差序列分析结果

对当前模型的评价：c=0.3390，很好；p=1.000 0，很好。

得到未来9 a的预测值，见表3。

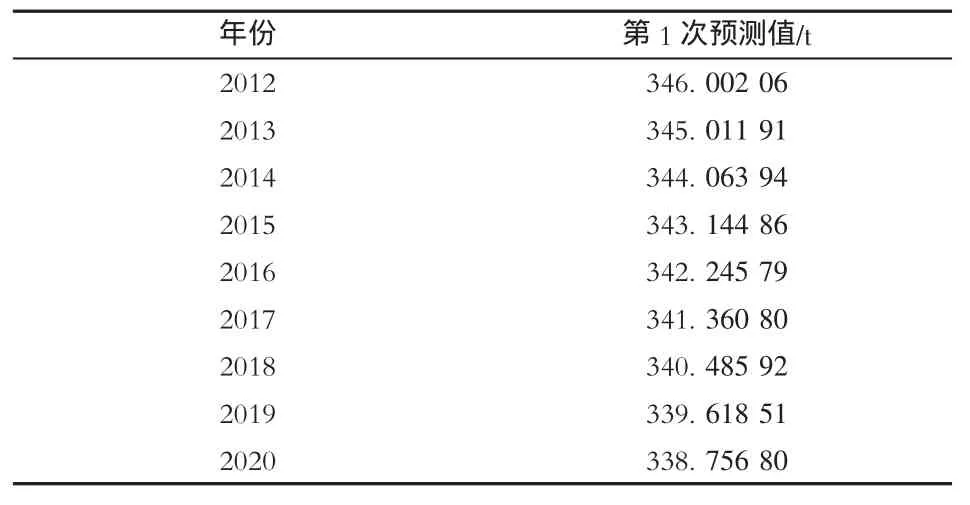
表3 GM（1，1）第1次残差序列分析得到的预测值

继续对残差序列进行建模分析。第2次残差序列分析得到表4。

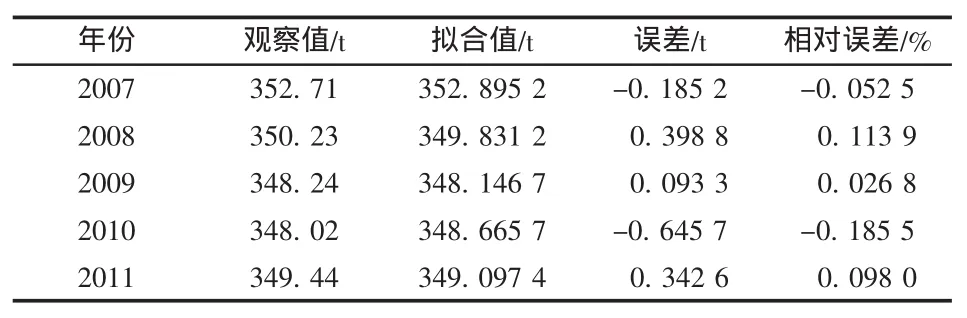
表4 GM（1，1）第2次残差序列分析结果

对当前模型的评价：c=0.211 1，很好；p=1.000 0，很好。以此得到未来9 a的预测值，见表5。

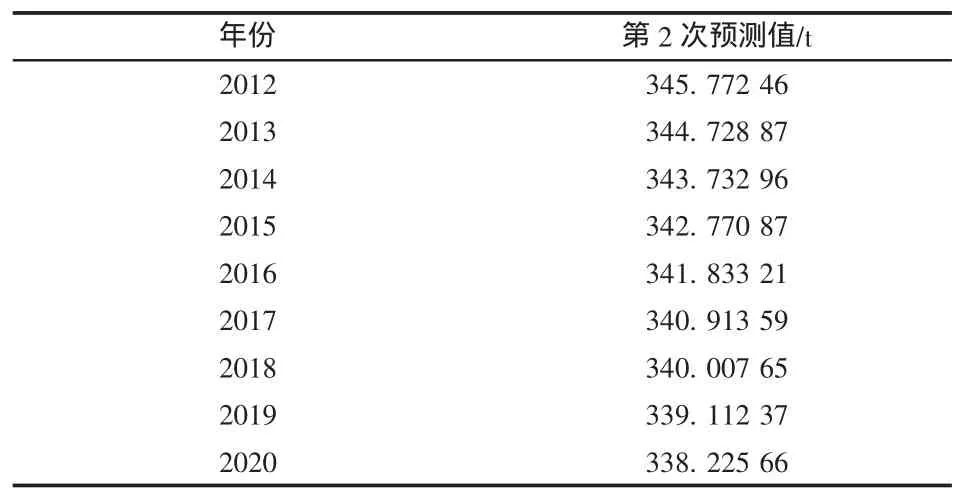
表5 GM（1，1）第2次残差序列分析得到的预测值

继续对残差序列进行建模分析。第3次残差序列分析得到表6。

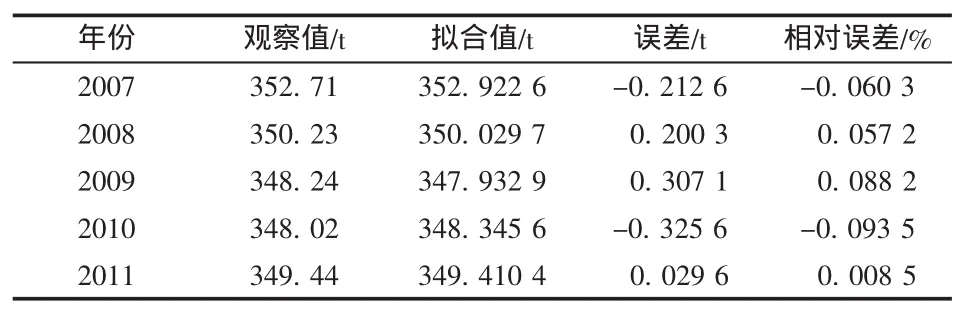
表6 GM（1，1）第3次残差序列分析结果

对当前模型的评价：c=0.1317 ，很好；p=1.000 0，很好。以此得到未来9 a的预测值，见表7。

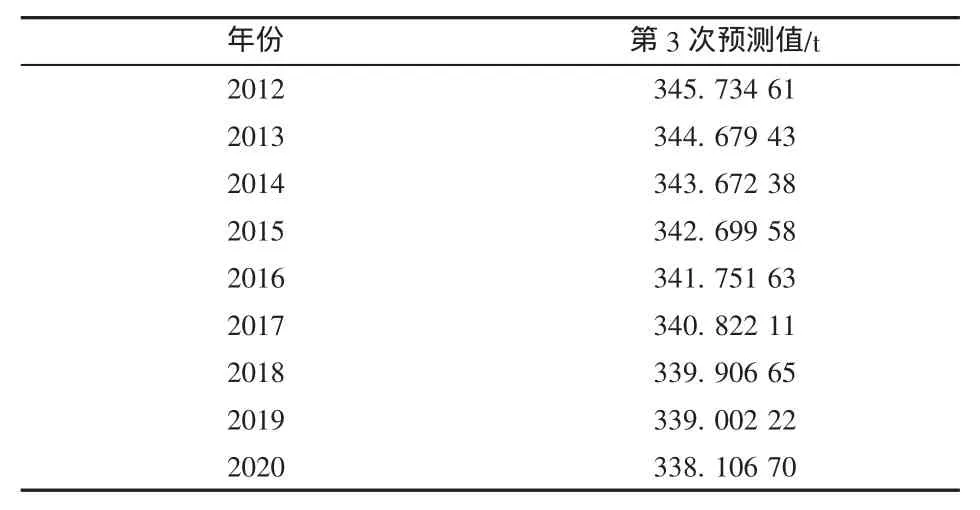
表7 GM（1，1）第3次残差序列分析得到的预测值

对3次残差序列得到的预测值进行比较得到图1，检验参数比较见图2。

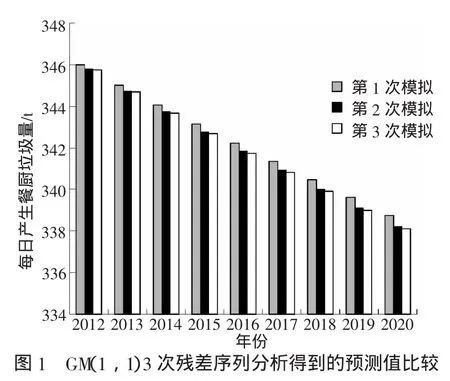
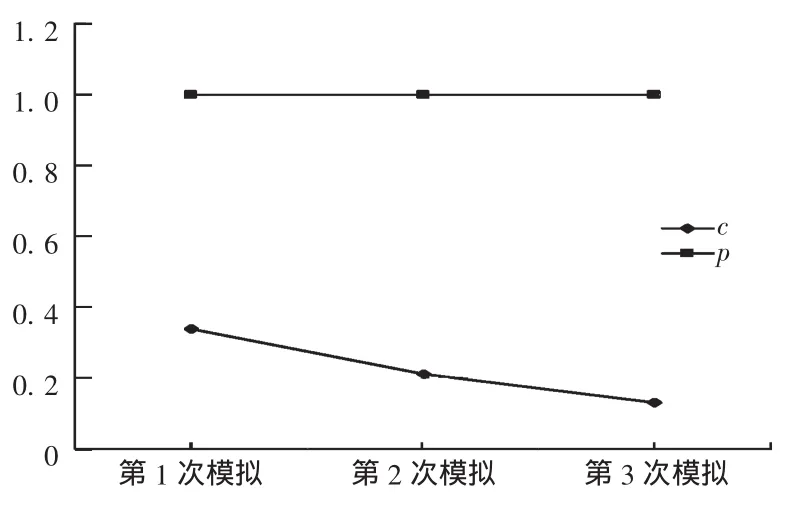
图2 检验参数比较

4 结论

通过GM（1，1）方法对济南市餐厨垃圾产量进行预测，得出：餐厨垃圾产生量与人口数量具有较高的相关性，随着人口素质的提高、“光盘行动”的开展，节能减排等理念的深入人心，餐厨垃圾的产生量应该呈现减少的趋势，此方法的预测也得到了较好的验证，证明GM（1，1）在餐厨垃圾的预测上效果良好，可以应用到华北地区其余地市的预测中。

[1]CJJ 184—2012餐厨垃圾处理技术规范[S].北京：中国建筑工业出版社，2013.

[2]唐启义.DPS数据处理系统[M].北京：科学出版社，2010.