干摩擦自激振动系统的滑模变结构控制

贾尚帅，李明高，李强，丁千

(1.中国北车集团 唐山轨道客车有限责任公司 产品技术研究中心，河北 唐山 063035;2.北京交通大学 机电学院，北京 100044;3.天津大学 机械工程学院，天津 300072)*

0 引言

干摩擦广泛存在于各种机械和工程结构当中，在系统低速运行时表现出强烈的非线性特性，会引起部件的振动和失稳，从而降低系统的性能.干摩擦系统的摩擦颤振是由于Hopf分岔导致系统失稳而产生的一种非常有害的高频振动［1-3］.合理的解决机械和工程中由于干摩擦引起的非线性振动极其稳定性问题，已成为当前该领域研究的重点问题.

分岔控制是抑制摩擦颤振的有效手段［4-5］.文献［6］将基于微分几何法和线性二次型最优控制方法结合在一起，针对刹车系统的分岔临界速度进行控制器设计.Chatterjee［7］通过 Lyapunov第二方法得到控制摩擦自激振动的控制率.Lignon等［8］证明μ-synthesis控制方法能够有效抑制刹车系统的自激振动.

本文考虑Stribeck摩擦力的两自由度干摩擦系统的动力学模型，利用平均法分析系统纯滑动自激振动的特性.设计滑模变结构控制器并推广其在干摩擦系统中的应用，有效地抑制摩擦颤振现象.

1 干摩擦自激振动

1.1 系统模型分析

图1为考虑Stribeck摩擦力的两自由度干摩擦系统的动力学模型.

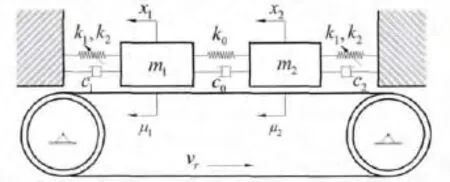
图1 考虑Stribeck摩擦力的两自由度干摩擦系统

当只考虑纯滑动运动，干摩擦自激振动系统的无量纲运动微分方程［9］.

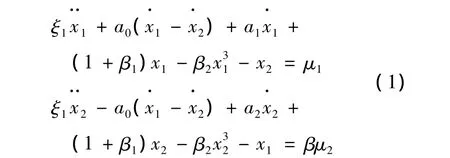
Stribeck摩擦力为

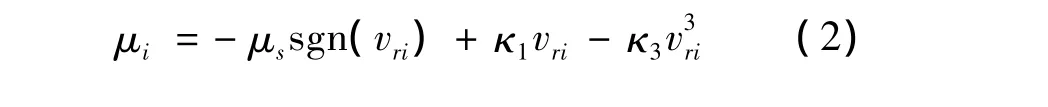
1.2 纯滑动运动分析

当传输带速度始终大于两质体的速度时为纯滑动运动，干摩擦力系数中的符号函数sgn(vri)=－1.

取系统参数为

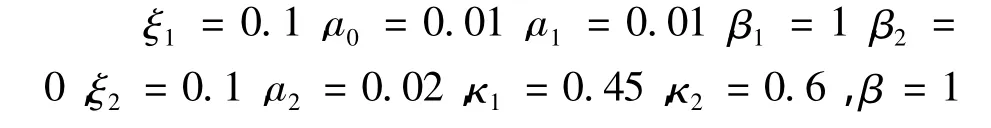
系统的平衡点

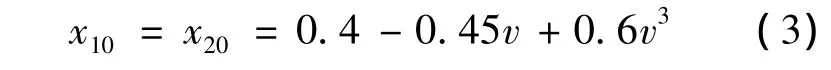
令

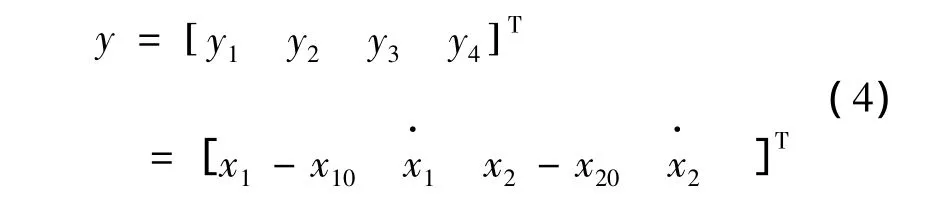
在阻尼项和非线性项前加入小参数，得到

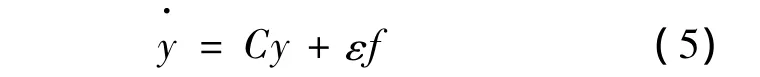
其中

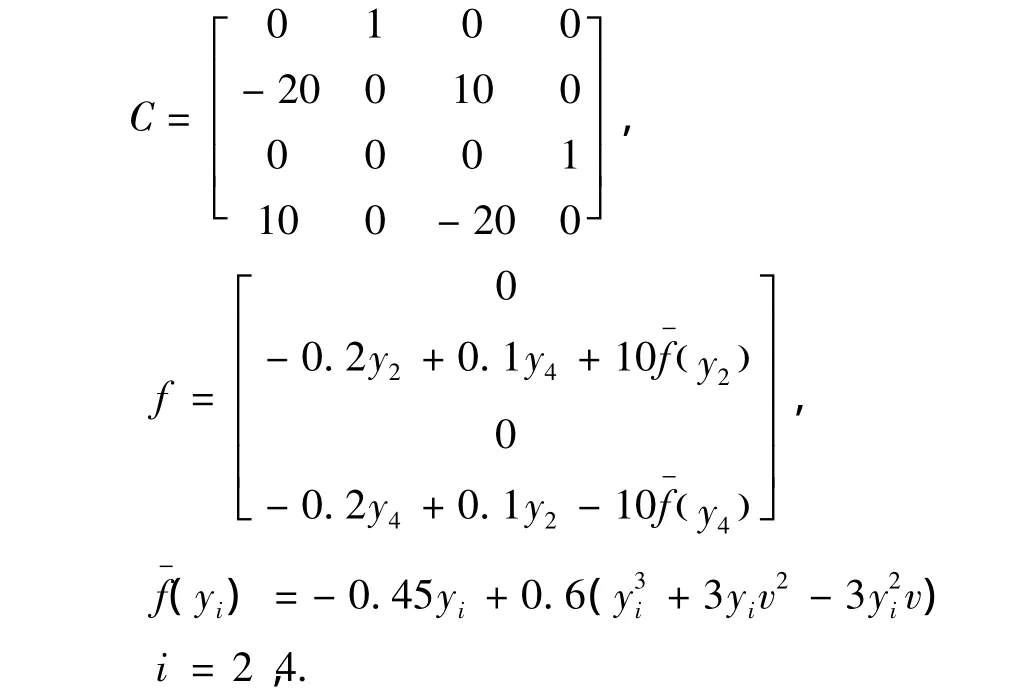
派生方程组为

对式(5)采用变换

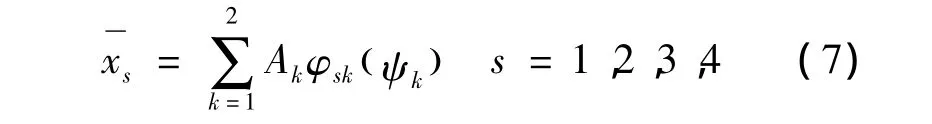
由派生方程组和共轭方程组基础解系正交关系

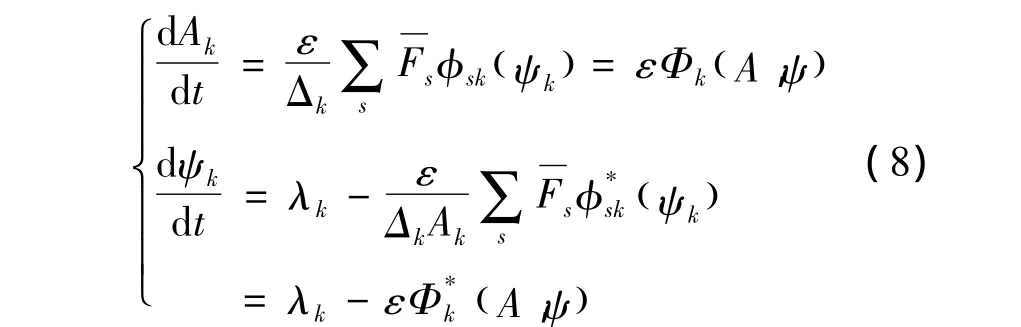
对式(8)应用KB变换

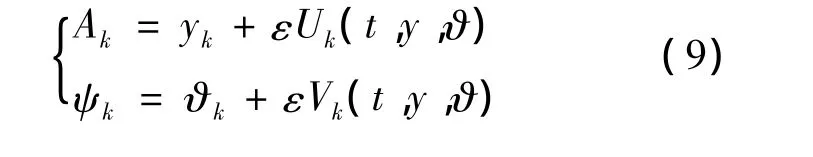
新变量

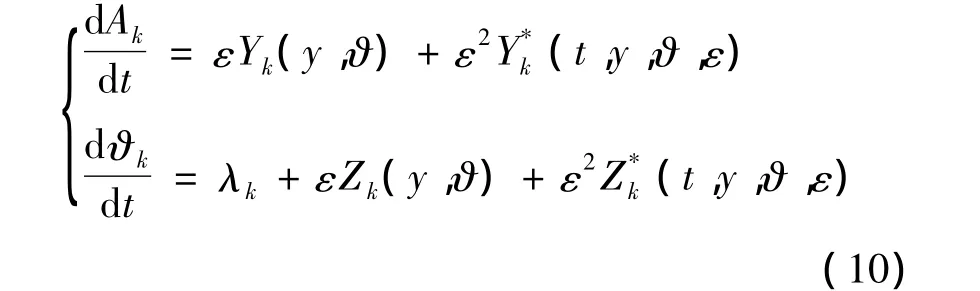
式中，Yk和Zk不显含时间t.Uk，Vk和为ϑ的以2π为周期的周期函数和t的周期函数.综合式(8)、(9)和式(10)得

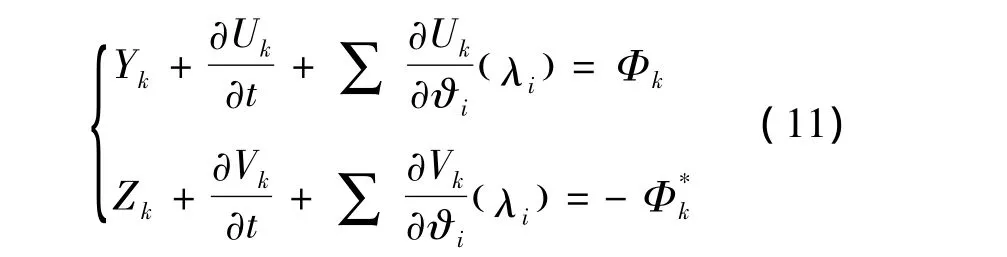
确定函数Yk和Zk

由式(6)λ1=5.5，λ2=3.2，Δ1=2.05，Δ2=1.95

进而得到一次近似解的振幅

令式(13)左边为零，得到定常解振幅

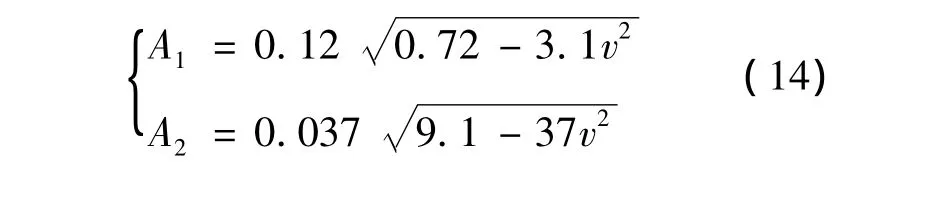
2 滑模变结构控制

针对干摩擦系统模型，将系统的数学模型写成仿射非线性形式

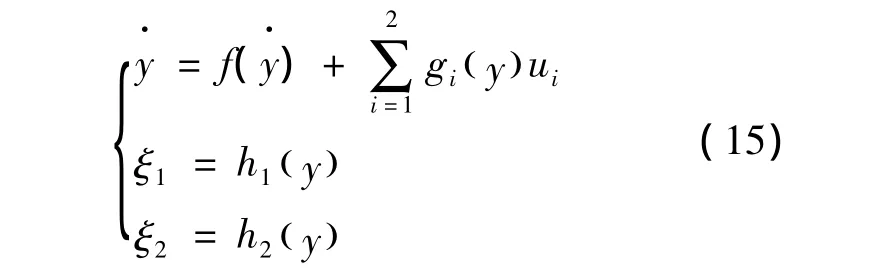
式中，y为状态变量同式(4);u为控制量;ξ为系统输出，其他表达式

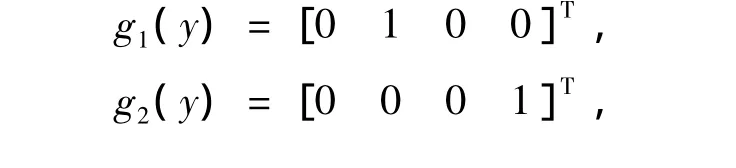
应用微分几何法，通过非线性状态反馈和坐标变换，将非线性系统精确线性化

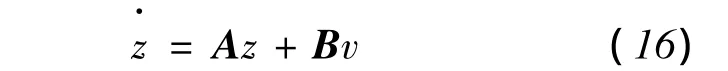
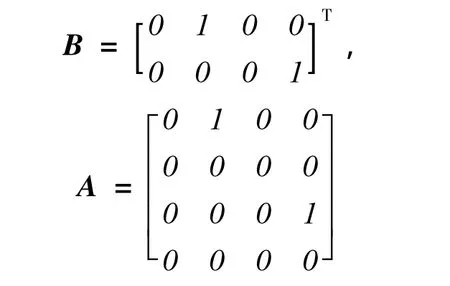
精确线性化得到的独立子系统式(16)为单输入单输出且状态变量是相变量的线性系统，当子系统进入滑动模态，其运动状态仅仅取决于相应的滑动面参数.

系统滑模变结构控制的原理图如图2，其中滑模控制器的设计包括切换面的设计和变结构控制律的设计.

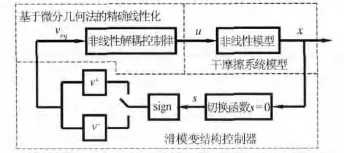
图2 控制原理图

对于系统(16)，设计切换方程

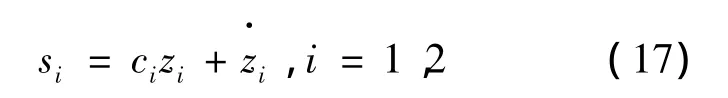
切换面s(z)=0通过原点，广义滑模存在条件为

式(18)为不等式条件，可以采用趋近律约束系统达到切换面

指数趋近律为

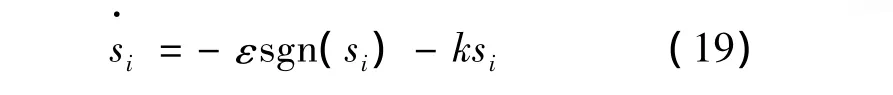
式(19)使得式(18)自然成立，并可得到等式

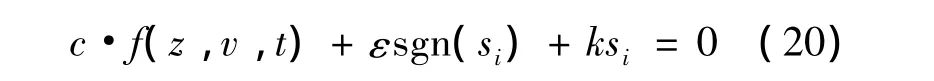
其中 c= ［ci1］，f(z， v， t)=Az+Bv.

变结构控制律

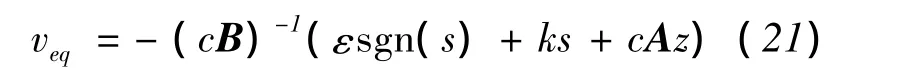
等效控制作用下的滑模运动方程为

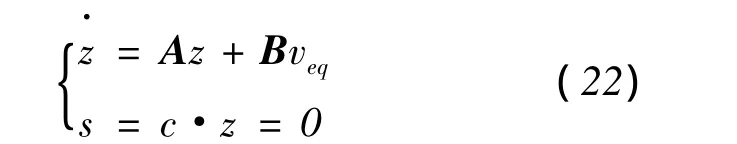
若使滑模状态反馈自治系统稳定，需要式(22)特征根无正实部，可以给定一组滑模面参数c，随后验证式(22)特征根条件是否成立，这样即满足滑模稳定性条件［10］.

3 仿真结果

系统参数同1.2中所示，采用四阶精度龙格-库塔法，考虑v=0.47的速度状态，SMC参数c=［1，1］，ε =5，k=10.

图3为两质体振幅的分岔图，由图可见，当v＞0.482和0.496时，m1和m2的定常解振幅为零，当v小于以上速度边界点时，产生自激振动且振幅随着v减小而增大，为典型的超临界Hopf分岔.

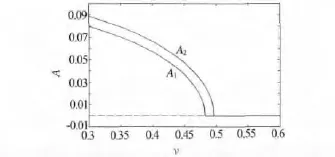
图3 分岔图

图4为质量块m1在控制函数作用下的状态轨线，由图可见，在颤振曲线上的初始点在趋近律的作用下迅速趋近到控制函数(s=0)，此时控制律在v+和v-间快速切换，系统状态在滑模面两侧穿行，最终系统状态沿设计的控制函数渐进稳定于平衡状态.

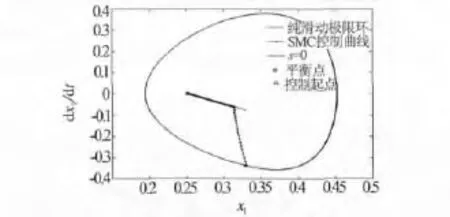
图4 SMC控制曲线图

图5为控制参数对抖振的影响，相应的控制参数ε=0.5，k=100时的抖振变小，即减小ε的同时增大k值有利于减弱SMC中的抖振现象.

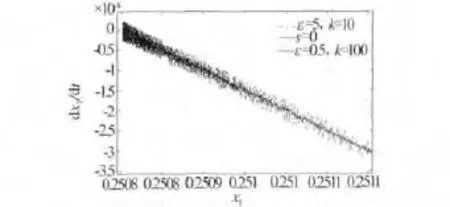
图5 控制抖振图

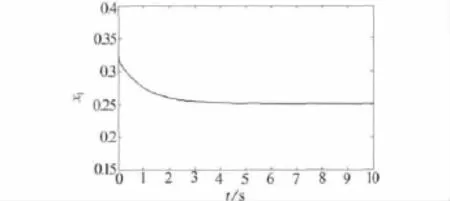
图6 渐进稳定曲线图

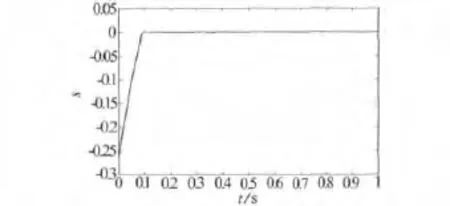
图7 切换函数

图6、图7分别为SMC渐进稳定曲线时间历程和切换函数，其中控制时间响应在经历3 s的振荡后稳定.

4 结论

研究干摩擦自激振动系统的振动特性及控制，应用滑模变结构控制方法，设计了非线性控制器，主要结论:①两自由度干摩擦系统纯滑动运动为典型的超临界Hopf分岔;②滑模变结构控制器能够有效抑制干摩擦系统的摩擦颤振，并具有一定鲁棒性;③通过调节ε、k可以有效地抑制控制器自身的抖振，提高控制系统的稳定性.

［1］丁千，陈艳，周翔.纯滑动形式的干摩擦自激振动研究［C］.第十一届全国非线性振动、第八届全国非线性动力学和运动稳定性学术会议，2007.

［2］黄毅.摩擦自激振动系统的非线性动力学特征与分岔控制研究［D］.天津:天津大学，2008.

［3］李博，丁千，陈艳.刹车系统摩擦自激振动的数值研究［J］.科技导报，2007，25(23):28-32.

［4］郭桂梅.摩擦自激系统的分岔控制研究［J］.机械强度，2009，31(4):523-526.

［5］黄毅，王太勇，张莹，等.机械系统中摩擦颤振机理的非线性分析［J］.中国机械工程，2008，19(14):1677-1680.

［6］贾尚帅，丁千.刹车系统的摩擦自激振动和控制［J］.工程力学，2012，29(3):252-256.

［7］CHATTERJEE S.Nonlinear control of friction-induced self-excited vibration［J］.International Journal of Nonlinear Mechanics，2007，42(3):459-469.

［8］LIGNON S，SINOU J J，JEZEQUEI L.Stability analysis and μ-synthesis control of brake systems［J］.Journal of sound and vibration，2006，298(4-5):1073-1087.

［9］黄毅，王太勇，李强，等.干摩擦系统的自激振动数值研究［J］.机械强度，2008，30(4):539-543.

［10］JEAN-JACQUES E.Slotine，Weiping Li，应用非线性控制［M］.北京:机械工业出版社，2006.