长江水系水质综合评价、预测的投影寻踪建模与实证研究

楼文高，熊 聘

（1.上海商学院，上海200235；2.上海理工大学 光电信息与计算机工程学院，上海200093）

长江水系水质综合评价、预测的投影寻踪建模与实证研究

楼文高1,2，熊 聘2

（1.上海商学院，上海200235；2.上海理工大学 光电信息与计算机工程学院，上海200093）

根据我国地表水环境质量标准和长江水系2006—2010年103个国控断面8个水质监测指标的数据，建立了长江水系水质综合评价的投影寻踪分类（PPC）模型。研究表明：在国控断面上，长江水系整体水质较好，Ⅰ～Ⅲ类水质占92.82%，其中Ⅰ类和Ⅱ类水质分别占62.52%和20.58%；上游水质好于下游水质；在化工工业较发达地区，Hg、石油类、挥发酚和氨氮的污染较严重，出现了劣Ⅴ类水质；与2009年相比，2010年水质出现了恶化。投影窗宽半径R值对PPC建模结果有显著影响，R取较小值方案（R=0.1Sz）和较大值方案（rmax≤R≤2p）都是不合理的，取中间适度值方案（rmax/5≤R≤rmax/3）才是合理和正确的。

长江水系；水质综合评价；投影寻踪建模；投影窗宽半径R值

长江水系为我国提供了近40%的水能资源，在国民经济发展中占有举足轻重的战略地位。然而，由于环境的严重污染导致长江水系水质污染也日益严重。为了对长江水系水资源进行充分利用、管理和正确规划提供科学的决策依据，必须对水系水质进行正确评价与预测。

水质综合评价方法有指数评价法、集对分析法、物元分析法、模糊数学法、灰色评价法、Logistic模型、主成分分析（PCA）、支持向量机（SVM）、人工神经网络（ANN）模型及其与ANN的组合评价等很多种方法（李惠明和尚广萍，1991；李祚泳等，2001；金菊良等，2003；楼文高和王延政，2003；陈润羊等，2008；刘小楠和崔巍，2009），这些方法各具特色与缺陷，如前五种方法必须首先由专家法和信息熵等主客观方法确定权重，结果的合理性随权重的合理性而改变，属于半定量研究方法；PCA方法必须满足大样本条件（MacCallum et al，1999），而且，样本不同，其评价结果也随之改变；ANN建模过程十分复杂，必须判定多种现象和确定多个合理参数，只有在遵循基本原则的前提下才可能取得可靠的结果（楼文高和王延政，2003；楼文高和乔龙，2011；StatSoft Inc，2011）；SVM模型须人为判定两个参数的合理值，等等。另一方面，Friedman and Tukey（1974）提出的可用于高维、非线性、非正态分布数据建模的投影寻踪分类（PPC）技术，自张欣莉等（2000）将其应用于水质评价以来，获得了广泛的应用（王顺久等，2002；封志明等，2005；付强和赵小勇，2006；楼文高和乔龙，2013）。但是，关于如何确定合理的窗宽半径R值以及判定最优化算法是否求得了真正的全局最优解，应用中也出现了不少错误和荒谬的结果。为此，考虑到数据的公开性和可获得性，本文根据《中国环境年鉴》中长江水系103个国控监测断面2006—2010年的主要水质指标监测数据，选取地表水环境质量标准（GB3832-2002）中DO、CODMn、Hg和NH3-N等8种主要污染物指标，采用PPC建模技术，综合评价研究长江水系所有国控断面的水质情况。研究结果表明：长江水系水质整体上以Ⅰ类（占62.52%）、Ⅱ类（占20.58%）和Ⅲ类（占9.71%）水质为主，但个别断面也出现了劣Ⅴ类水质的情况。并且研究了不同R值对建模结果的影响以及出现的明显错误，进而提出了选取R值的合理范围。

1 水质综合评价PPC建模原理简介

1.1 长江水系水质监测指标及其评价标准

根据《中国环境年鉴》（2007—2011年）列出的长江水系国控断面9个主要监测指标2006—2010年的年均值，因为Ⅰ～Ⅴ级水质的pH值均为6～9，故我们选取DO、CODMn和NH3-N等8个主要监测指标来综合评价长江水系的水质。我国地表水环境质量标准（GB3832-2002）如表1所示，同时，根据五级水质的指标值及其变化规律或者趋势以及长江水系水质指标实测值的范围确定了各指标的最大值和最小值（也列于表1中）。

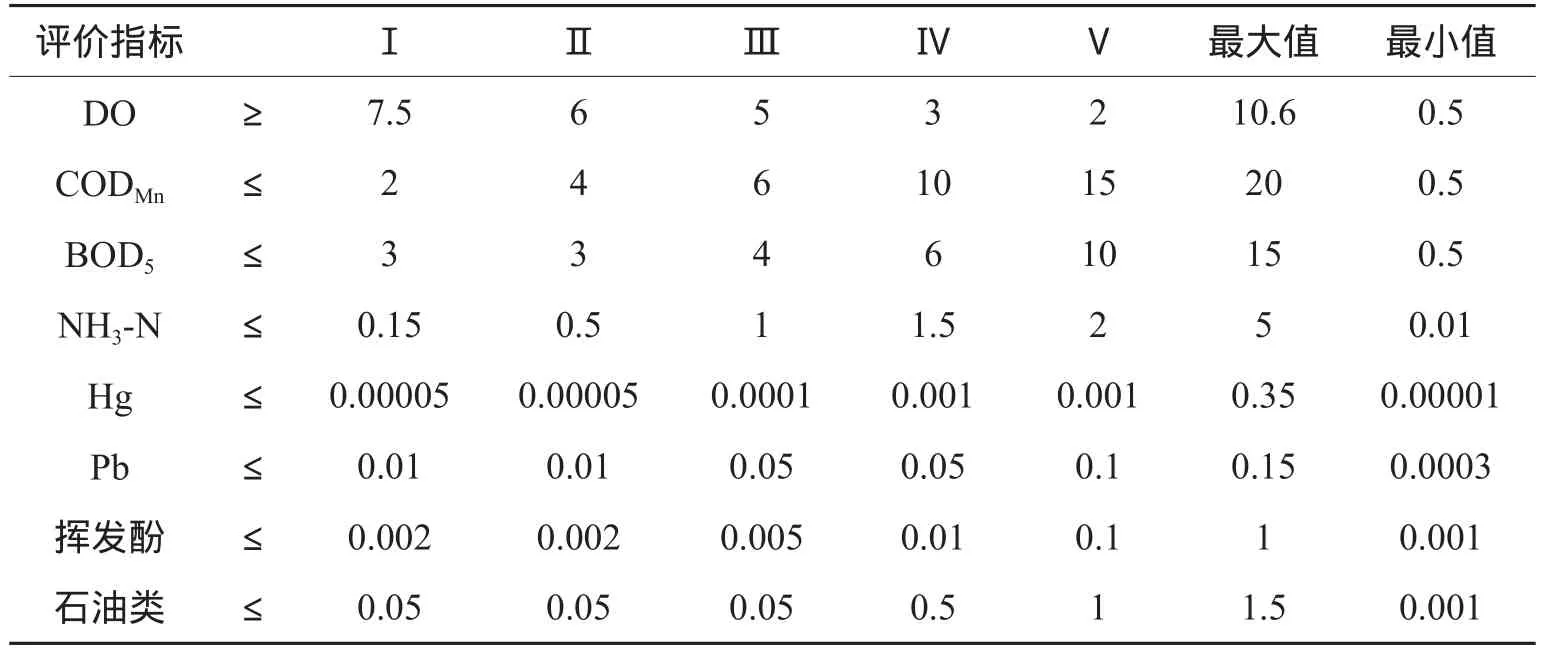
表1 地表水环境质量标准（GB3838-2002）Table 1 Environmental quality standards for surface water

1.2 水质综合评价PPC建模原理简介

根据表1的水质评价标准，可用由Friedman and Tukey（1974）提出并被张欣莉等（2000）首先采用、后被国内其他学者广泛采用的一维PPC模型（王顺久等，2002；封志明等，2005；付强和赵小勇，2006；楼文高和乔龙，2013）建立长江水系水质综合评价模型。Friedman等提出“应使样本投影点整体上尽可能分散，局部上尽可能密集”（Friedman and Tukey，1974；张欣莉等，2000），其目标函数为使样本投影值标准差Sz与局部密度值Dz乘积的最大化，即：

由上式可知，投影密度窗口半径R值显著影响其最优化结果——最佳投影向量以及样本投影值，楼文高和乔龙（2013）深入研究了R值的本质及其对建模结果的影响，进而提出了选取R值的合理范围应该为rmax/5≤R≤rmax/3，即平均有1/5～1/3的样本点在投影窗宽内。由于（1）式为高维、复杂的非线性不等式约束最优化问题，很难求得真正的全局最优解。笔者采用群搜索算法（GSO）对（1）式进行最优化求解。

2 建立水质综合评价PPC模型及其长江水系的水质与变化趋势

为了消除水质指标不同量纲对建模结果的影响，本文对表1的各指标值进行开放性更好的（即实际样本的最大值和最小值可以大于或者小于表1所示的最大值和最小值）零均值归一化（即均值为0，方差为1）处理，而对DO先进行正向化处理，即所有指标的归一化值越大，相应的投影值也越大，其水质就越差。把各样本归一化数据导入笔者研发的基于GSO算法的PPC程序，得到了R=rmax/5时的PPC建模结果，即最佳投影向量a1～8=（0.143，0.252，0.336，0.367，0.488，0.287，0.484，0.338），各样本的投影值z(1) ～ z(7)=（−2.102，−1.643，−1.436，−0.938，−0.205，1.052，5.272），样本投影值标准差Sz=2.550，局部密度值Dz=23.102，目标函数值Q(a) = 58.899，投影窗宽半径R=1.475，样本之间的最大距离rmax=7.374。由五个标准样本的意义可知，Ⅰ～劣Ⅴ类水质的投影值范围分别为小于等于−1.643、（−1.643，−1.436]、（−1.436，−0.938]、（−0.938，−0.205]、（−0.205，1.052]和大于1.052。

对《中国环境年鉴》给出的长江水系103个国控断面的8个主要监测指标值，也进行相同的零均值归一化处理，再代入上述PPC模型，就得到了各个国控断面2006—2010年的水质投影值z(i)，根据上述各级不同水质的投影值范围，就可以很便捷地判定各断面的综合水质类别。为节省篇幅，表2仅列出各省市交界的典型国控断面和苏州、上海等合计22个断面的PPC模型投影值及其综合评价的水质类别。

由研究结果和表2可知，长江水系国控断面的水质呈以下特征：（1）综合评价水质以Ⅰ类和Ⅱ类为主，在515个样本（103个断面、五年）中，Ⅰ类水质322个，占62.52%，Ⅱ类水质106个，占20.58%；（2）2006—2010年分别有37个、24个、17个、10个和15个断面的综合水质最差，说明整体上长江水系水质有所改善，沿长江流域各省市或者城市的水污染治理工程发挥了重要作用，基本遏止了水质恶化的趋势，如沿河断面、鲢鱼溪断面的水质从Ⅱ类变为Ⅰ类，新甸铺断面水质从Ⅳ类变为Ⅲ类，吴淞口水质从Ⅲ类变成Ⅱ类；但与2009年相比，2010年水质整体上有所恶化；（3）上游水质要好于下游水质，流经大城市的水质相对较差（如苏州、上海等）；（4）流经安徽、四川、江苏和湖北等省市后的综合水质明显变差，这些省市必须采取切实有效措施，进一步加大水污染治理力度，彻底扭转这种状况。

3 结果与讨论

3.1 各水质评价指标重要性分析

根据PPC建模的最优化结果，8个评价指标都是重要的，但从重要性来看，Hg最重要，其次是挥发酚，然后是NH3-N、石油类、BOD5、Pb、CODMn等，DO最不重要，权重最大值与最小值之比达到了3.4倍，说明它们的差异显著。因此，从整体上有效改善长江水系综合水质的角度来看，首先应显著减少Hg和挥发酚的排放，其次是明显降低石油类、氨氮、BOD5和Pb等的排放，这样才能起到事半功倍的效果，否则，往往事倍功半，起不到明显的效果。

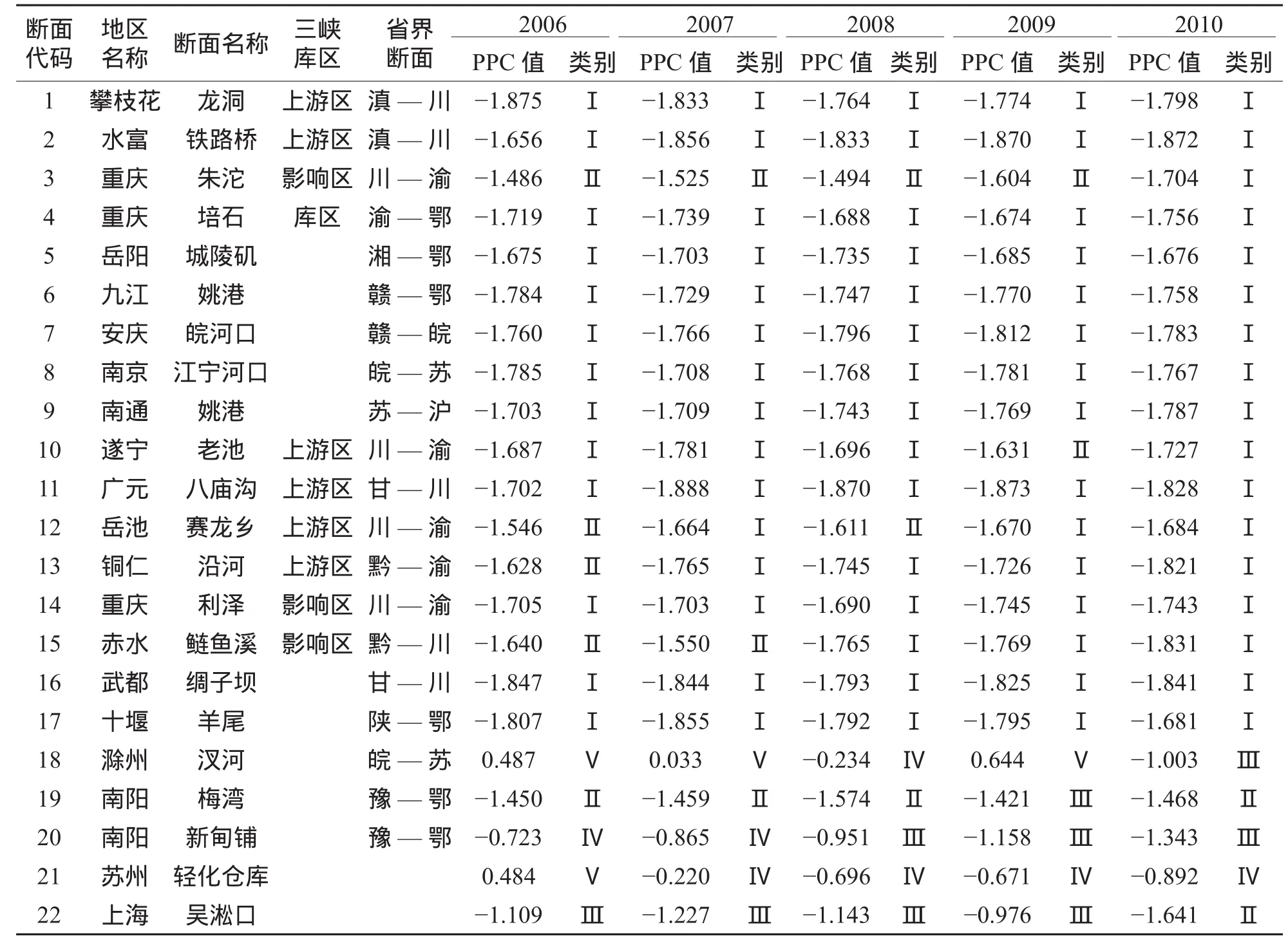
表2 长江水系典型国控断面水质投影值、综合评价结果及其类别Table 2 The projected values and the type of the water quality in the typical state-controlled sections of Yangtze River

3.2 长江水系整体水质情况及其变化趋势分析

根据103个国控断面2006—2010年的水质综合评价结果可知，长江水系整体水质呈如下特征：（1）长江水系综合水质处于良好状态，以Ⅰ类和Ⅱ类水质为主，其中Ⅰ类、Ⅱ类和Ⅲ类分别占62.52%、20.58%和9.71%，而Ⅳ和Ⅴ类分别仅占4.08%和1.75%，劣Ⅴ类占1.36%。（2）介于省市分界的国控断面综合水质有所好转，说明各省市都十分重视水污染治理工程，并取得了显著效果；与此同时，在103个国控断面上，虽然2007—2009年期间水质有所好转，但2010年的水质差于2009年（如：衡阳从Ⅱ类水质变成Ⅲ类，六盘山从Ⅱ类变成Ⅴ类）。这是否意味着各省市放松了对水环境污染的治理？值得我们反思和警惕。（3）上游地区（断面）水质好于下游地区，大城市（断面）水质比其他区域水质差。（4）长江水系在贵州省、四川省、江西省、安徽省、湖北省和江苏省的水质较差，应该是长江水系水环境污染治理的重点。由于这些区域酿酒业、造纸业、皮革加工业等化工工业发展迅速，工业污水虽经处理，但水体中Hg、石油类、挥发酚和氨氮等的含量仍然较高，导致水质大多低于Ⅲ类，有些断面甚至出现了Ⅴ类和劣Ⅴ类水质，水污染情况十分严重。

3.3 窗宽半径R值对PPC建模结果和长江水系水质评价结果的影响

R值是决定PPC模型最优化结果的唯一参数，但不同的学者提出了多种不同的选取R值的方案：（1）Friedman and Tukey（1974）提出较小值方案，即R = 0.1Sz或者更小的R = (0.01～0.001)Sz（张欣莉等，2000；封志明等，2005）；（2）王顺久等（2002）提出取较大值方案，取rmax≤R≤2p，通常取R= p；（3）楼文高和乔龙（2013）提出取中间适度值方案，通常取rmax/5≤R≤rmax/3。

取较小值方案时，窗宽半径内只包含很少的样本点，取较大值方案时，窗宽半径内包含了所有的样本点，取中间适度值方案，窗宽半径内样本点既不太多，也不太少。那么，三种选取R值的不同方案将对PPC建模结果产生怎样的影响呢？到底哪个方案更合理？建模结果更可靠？

为了分析R值对PPC建模结果的影响规律，笔者分别取R≤0.001Sz、0.01Sz、0.05Sz、0.1Sz、0.25Sz、0.5Sz、rmax/5、rmax/4、rmax/3、Sz、rmax/2、rmax和R = p = 8建模，表3所示为取不同R值时的PPC建模结果。分析上述建模结果，可以得到如下规律：（1）R∈[0.001Sz，0.25Sz]时，最佳投影向量发生了很明显的改变，且没有规律性，而且部分指标的性质是错误的（即表3中权重小于0的情况，下同），如a1从0.328变为−0.328、0.057、−0.013、−0.024，而且最优化过程往往无法求得真正的全局最优解，针对每个R值，笔者通过调整不同的参数组合，应用群搜索算法或者混沌ABC算法计算30余次，表3所示是计算所得的最好结果，但还不是真正的全局最优解；（2）R≤0.001Sz或R≥rmax时，最优化结果很稳定，而且基本相同，在此范围内，R值越小或者越大，各指标权重变化越小；（3）R∈[0.5Sz，rmax/2]时，最优化过程很容易求得真正的全局最优解，所有指标的性质都是正确的，最佳投影向量和各样本投影值随R值变化而改变，但相差不是很大，体现了PPC建模可以揭示出高维数据不同结构特点的精髓。

此外，还有不少文献取R为常数，为此笔者取R=10−5、10−4、10−3以及与表3基本对应的R值（如0.0027、0.068、0.138、0.360、1.260、1.470、1.900、2.500、3.800、7.800）、10和100分别建模，表4所示是其PPC建模结果。由表4可知，建模结果的规律与R取非常数时基本一致，但也表现出不同的特点：（1）R∈[10−5，1.900]（1.900相当于rmax/2.63或者1.04Sz）时，部分指标的权重出现了小于0的情况，如a1≤0的情况（用波浪线表示小于0，下划线表示几乎为0，下同），这些指标的性质肯定是错误的。此外，出现了多个指标的权重同时为0的情况（如R=0.0027时），这种情况肯定也是错误的；（2）R∈[10−4，0.068]时，出现了多个样本值相等的情况，事实上，这些样本值是区分不同类别水质的分界值，如果都相等，无法区分不同水质等级，所以也肯定是不合理的；（3）虽然R大于3.800（相当于rmax/2）时，最优化过程能求得真正的全局最优解，但R=3.800时a1的权重仅为0.036，明显小于其实际值，也是不合理的。R=7.800（此时R已大于rmax）的权重与非常数时R = rmax/3的权重基本相当；（4）当R≤10−5或R≥50时，各个指标的权重才基本稳定不变。

因此，R取常数时第（2）～（4）个规律与取非常数时的规律不同。而且，即使R值基本相同，取常数与非常数的建模结果（权重等）却相差很大。为此，笔者认为R为常数也是不合理的。

3.4 不同群智能最优化算法的性能比较

笔者用多种改进PSO（IPSO）、多种遗传算法（GA）、基于实数编码的加速遗传算法（RAGA）（该最优化算法已被很多学者用于PPC建模）、多智能体遗传算法（MGA）、人群搜索算法（SOA）、遗传-PSO组合算法（GA-PSO）、鸡群算法（CSO）、果蝇算法（FOA）、人工鱼群算法（AFSA）、萤火虫算法（FFA）、布谷鸟搜索算法（C-SO）、蚁群算法（ACO）、蚁狮算法（ALO）、差分算法（DA）、和声搜索算法（HS）、灰狼搜索算法（GWO）、资源竞争算法（COR）、蜘蛛算法（SSO）、花授粉算法（FPA）、细菌算法（BFO）、重力搜索算法（GSA）、群搜索算法（GSO）和人工蜂群算法（ABC）等对PPC模型进行最优化求解。针对每种算法，通过调整不同的参数组合，平均计算30次以上，研究发现：（1）在R取中间适度值和较大值方案时，绝大多数群智能算法都基本能求得真正的全局最优解，但收敛速度和收敛性能有较大差异，其中ABC、GSO、GSA、GWO、ALO、SOA、IPSO和CSO等的收敛速度较快，也基本每次都能求得真正的全局最优解，而其他方法则往往收敛较慢，也不能保证每次都求得真正的全局最优解；（2）R取较小值方案时（如R∈[0.001Sz，0.25Sz]或者R∈[10−4，0.360]），上述群智能最优化算法往往都不能求得真正的全局最优解，但是，在接近全局最优解邻域范围内，GSO、GSA、ABC和MGA的收敛性能较好，收敛速度也较快，应优先推荐使用，而其他方法，无论是收敛性能还是收敛速度，都不太理想；（3）被很多学者用于PPC建模的RAGA和ACO等算法，其收敛性能和收敛速度都明显差于ABC、IPSO、GSO、GSA和SOA等算法。

为了从理论上进一步研究上述实证研究结果所表现出来的规律性，笔者分析讨论如下：

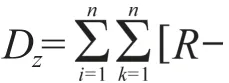
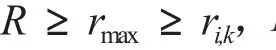
从上述实证结果和理论分析可知，R取很小的值和较大值方案时，PPC建模结果必定是相同的，而且都只使Sz最大化，即仅仅达到了“使样本投影点整体上尽可能分散”的目标，而没有同时实现“使样本点局部尽可能密集”的目标，没有完全实现Friedman and Tukey（1974）提出的PPC建模的目标，是不合理的。而且，R取较小值方案时，R值不同，PPC建模结果也不同，有时会出现很大的变化，也没有规律性可循。另一方面，R取中间适度值方案时，目标函数完整体现了Friedman等提出的PPC建模基本思想——“样本投影点整体上尽可能分散，局部尽可能密集”的要求，所以是合理和正确的。

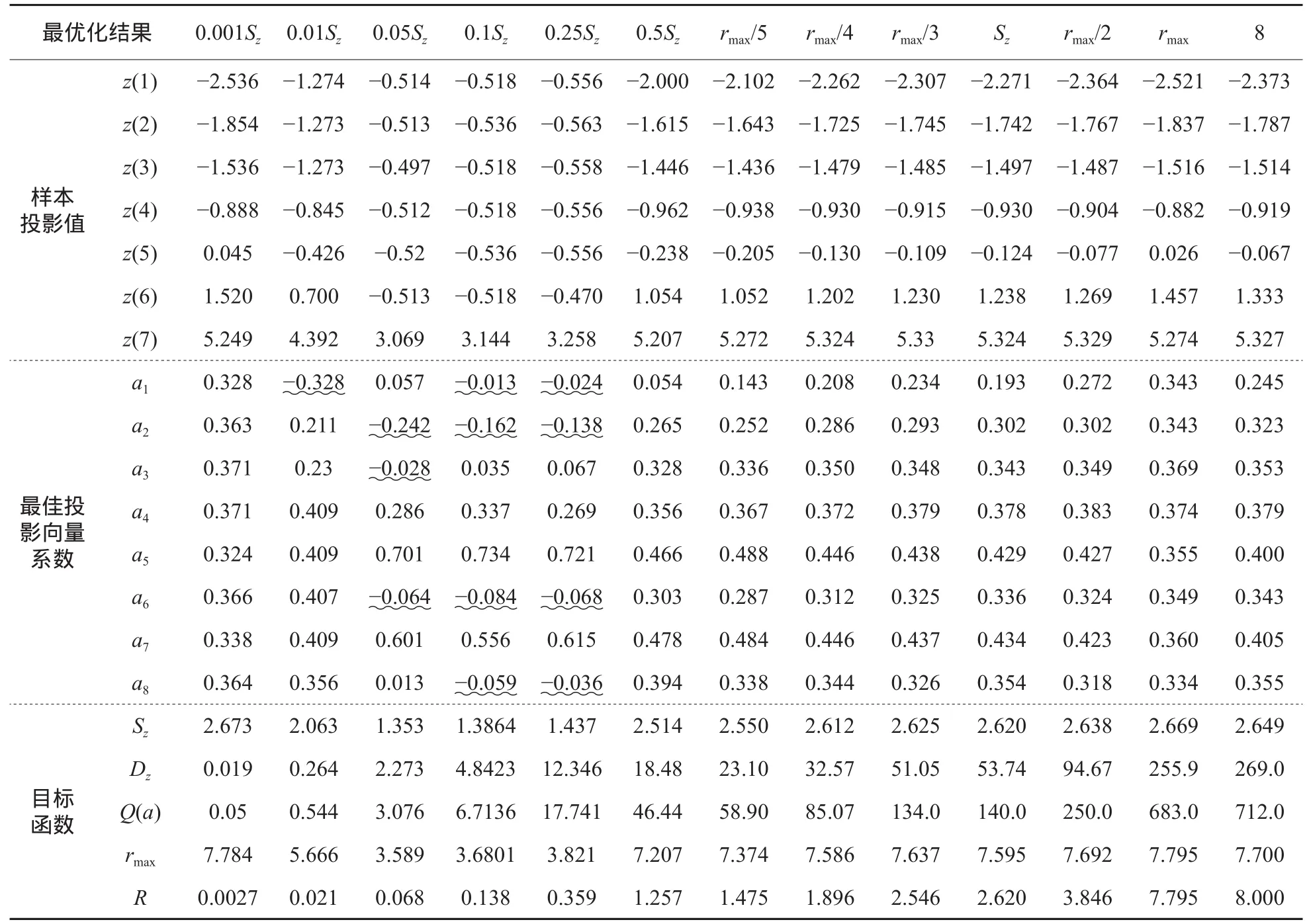
表3 窗宽半径 取不同值（三种方案）时的PPC建模结果对比Table 3 Comparison of PPC model in different cutoff radius R (three methods)

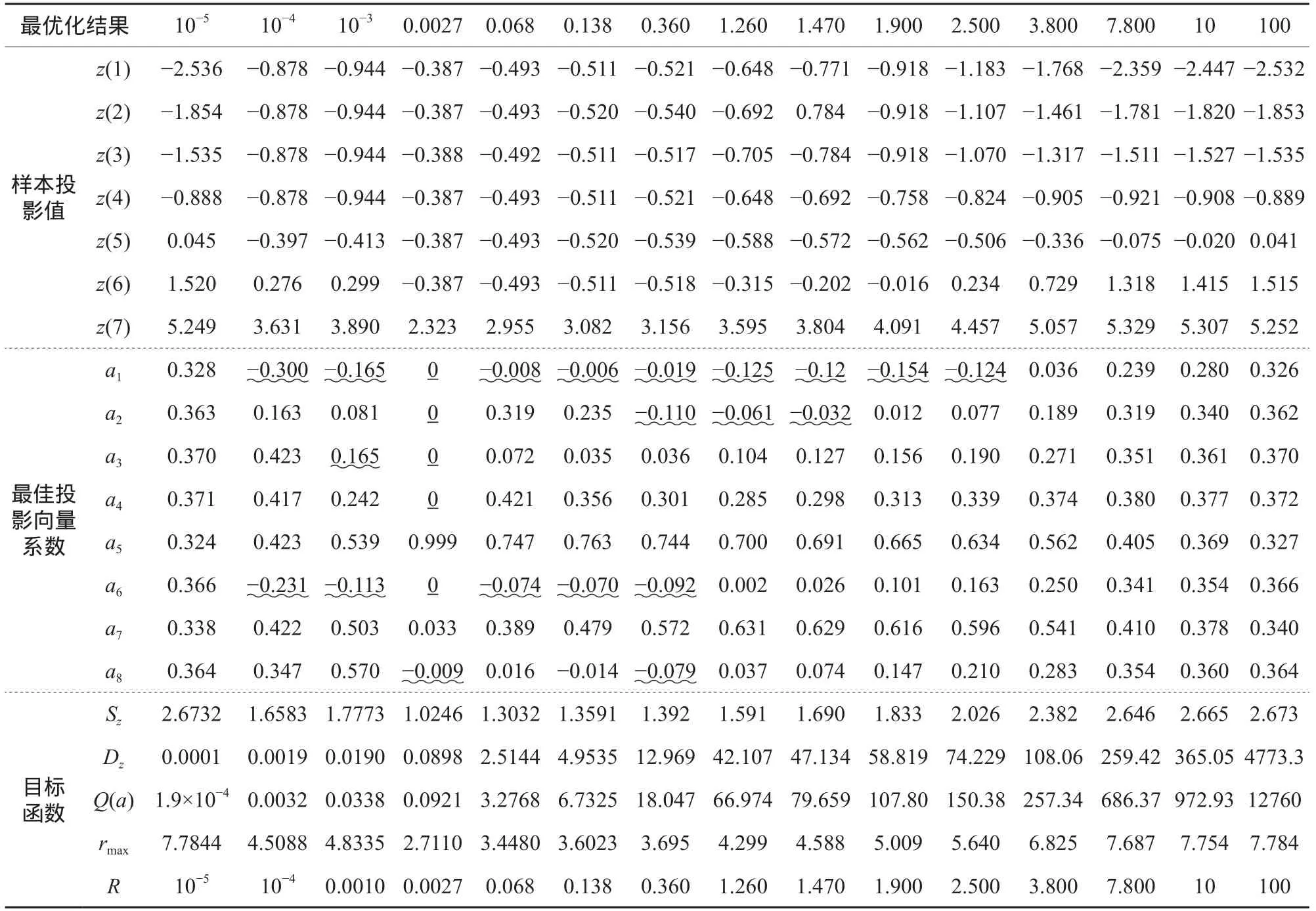
表4 窗宽半径R取不同值（常数）时的PPC建模结果对比Table 4 Comparison of PPC model in different cutoff radius R (constant)

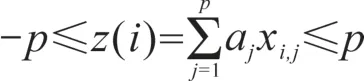
3.5 R在中间适度值（rmax/5≤R≤rmax/3）范围内取不同值对水质综合评价结果的影响

笔者也建立了R=rmax/3时的PPC模型，其结果如表3所示。与R=rmax/5时的建模结果相比，各个指标的重要性更均衡化，即小的权重都得到了一定程度的提高（如a1从0.143到0.234，a2从0.252到0.293），大的权重都有不同程度的下降（如a5从0.488到0.438，a8从0.338到0.326），即Hg、挥发酚和石油类指标对水质的影响程度有所降低，而其他指标的影响程度则都有所提高，致使DO较低以及CODMn和Pb较高断面的水质评价结果将变差，而Hg和挥发酚较高断面的水质评价结果将变好。就22个国控断面110个样本而言，有4个样本的水质类别出现了改变，其中分别有1个样本从Ⅳ类变为Ⅲ类和从Ⅲ类变为Ⅱ类，2个样本从Ⅱ类变为Ⅰ类。

因此，无论R=rmax/5还是R=rmax/3，绝大多数样本（占96%）的水质类别都保持不变。同时，由于显著提高了DO的影响程度，改变了少部分水体的水质类别，但从PPC模型输出值是实数的结果来看，改变类别的水质都处于相邻类别水质的分界点附近，对水质实际评价结果的影响并不大。

4 结束语

（1）根据典型国控断面的水质监测指标数据和我国地表水环境质量标准，建立了长江水系水质综合评价的投影寻踪分类（PPC）模型，得到了2006—2010年103个国控断面的水质综合评价结果。长江水系在国控断面上整体水质较好，Ⅰ～Ⅲ类水质占92.82%，其中Ⅰ类水质占62.52%，Ⅱ类水质占20.58%。流经四川、安徽、江苏等省后，水质明显下降；整体上，上游水质好于下游水质。在化工工业较发达的地区，Hg、石油类、挥发酚和氨氮的污染较严重，出现了劣Ⅴ类水质，水污染现象较严重。在2007—2009年期间，水质整体上有明显好转，但2010年的水质比2009年的水质差，如果任其发展，前期的治理成效将可能前功尽弃。因此，当地政府和有关环保部门，水污染治理工作任重道远，必须采取更严厉的措施，彻底扭转这种恶化趋势，始终保持水污染治理的高压态势，绝不能有丝毫的懈怠和放松。

（2）实证和理论研究都表明，投影窗宽半径R值对PPC建模结果具有重要影响或者说是决定其结果的唯一参数，目前选取R值的较小值方案和较大值方案都是不合理的和错误的。在R取很小值（如小于0.001Sz）和很大值（如大于2rmax）时，目标函数都只能体现Friedman等提出的“使样本投影点整体上尽可能分散”的要求，未能实现“样本点局部上尽可能密集”的目标。而且，当R取较小值时，各指标权重的细微改变就可能引起目标函数值的变化，目标函数存在很多局部极小点，致使最优化过程通常都无法求得真正的全局最优解，即使求得了真正的全局最优解，建模结果也没有规律性。R取中间适度值时，目标函数完整体现了Friedman等提出的PPC建模的基本思想，而且，在此范围内取不同的R值，对建模结果的影响并不大，具有很好的规律性，最优化过程也都能求得真正的全局最优解。R取常数时也不能得到合理的结果。

（3）采用多种群智能算法对PPC模型进行最优化求解，结果表明，GSO、GSA、ABC和MGA的收敛性能较好，收敛速度也较快，应优先推荐使用。

陈润羊, 花 明, 涂安国. 2008. 长江水系水质评价的几种方法[J]. 东华理工大学学报(自然科学版), 31(2): 146–151. [Chen R Y, Hua M, Tu A G. 2008. Several methods of water environment quality assessment in the Yangtze River [J]. Journal of East China Institute of Technology, 31(2): 146–151.]

董玉才, 范格华, 张 玲, 等. 2011. 基于投影寻踪法的坦克动力舱热工况综合评价[J]. 数学的实践与认识, 41(17): 157–161. [Dong Y C, Fan G H, Zhang L, et al. 2011. Integrated evaluation on thermal working condition in tank power cabin based on projection pursuit method [J]. Mathematics in Practice and Theory, 41(17): 157–161.]

封志明, 郑海霞, 刘宝勤. 2005. 基于遗传投影寻踪模型的农业水资源利用效率综合评价[J]. 农业工程学报, 21(3): 66–70. [Feng Z M, Zheng H X, Liu B Q. 2005. Comprehensive evaluation of agricultural water use eff ciency based on genetic projection pursuit model [J]. Transactions of the CSAE, 21(3): 66–70.]

付 强, 赵小勇. 2006. 投影寻踪模型原理及其应用[M]. 北京:科学出版社. [ Fu Q, Zhao X Y. 2006. The Principles and Applications of Projection Pursuit Model [M]. Beijing: Science Press.]

金菊良, 刘 丽, 丁 晶, 等. 2003. 地下水水质评价的逻辑斯谛曲线模型[J]. 环境污染与防治, 25(1): 46–48. [Jin J L, Liu L, Ding J, et al. 2003. Logistic curve model of groundwater quality evaluation [J]. Environmental Pollution and Control, 25(1): 46–48.]

李惠明, 尚广萍. 1991. 水质现状评价数学模型综合研究[J].中国环境科学, 11(5): 356–360. [Li H M, Shang G P. 1991. A comprehensive study on the mathematical models of water quality evaluation [J]. China Environmental Science, 11(5): 356–360.]

李祚泳, 郭丽婷, 欧阳洁. 2001. 水环境质量评价的普适指数公式[J]. 环境科学研究, 14(3): 56–58. [Li Z Y, Guo L T, Ou Y J. 2001. An universal formula suited to water quality evaluation [J]. Research of Environmental Sciences, 14(3): 56–58.]

刘小楠, 崔 巍. 2009. 主成分分析法在汾河水质评价中的应用[J]. 中国给水排水, 25(18): 105–108. [Liu X N, Cui W. 2009. Application of principal component analysis method to assessment of water quality in Fen River [J]. China Water and Wastewater, 25(18): 105–108.]

楼文高, 乔 龙. 2011. 基于神经网络的金融风险预警模型及其实证研究[J]. 金融论坛, (11): 52–61. [Lou W G, Qiao L. 2011. Early warning model of f nancial risks and empirical study based on neural network [J]. Finance Forum, (11): 52–61.]

楼文高, 乔 龙. 2013-08-30. 投影寻踪分类建模理论的新探索与实证研究[J/OL]. 数理统计与管理, 2015(1), http://www.cnki.net/kcms/detail/11.2242. O1.20130830.1736.001.html. [Lou W G, Qiao L. 2013-08-30. New theory exploration of projection pursuit clustering model and its positive research [J/OL]. Journal of Applied Statistics and Management, 2015(1), http://www.cnki.net/ kcms/detail/11.2242.O1.20130830.1736.001.html.]

楼文高, 王延政. 2003. 基于BP网络的水质综合评价模型及其应用[J]. 环境污染治理技术与设备, 7(4): 23–26. [Lou W G, Wang Y Z. 2003. Water quality comprehensive assessment model using BP networks and its applications [J]. Techniques and Equipment for Environmental Pollution Control, 7(4): 23–26.]

王顺久, 张欣莉, 丁 晶, 等. 2002. 投影寻踪聚类模型及其应用[J]. 长江科学院院报, 19(6): 53–55, 61. [Wang S J, Zhang X L, Ding J, et al. 2002. Projection pursuit cluster model and its application [J]. Journal of Yangtze River Scientif c Research Institute, 19(6): 53–55, 61.]

张欣莉, 丁 晶, 李祚泳, 等. 2000. 投影寻踪新算法在水质评价模型中的应用[J]. 中国环境科学, 20(2): 187–189. [Zhang X L, Ding J, Li Z Y, et al. 2000. Application of new projection pursuit algorithm in assessing water quality [J]. China Environmental Science, 20(2): 187–189.]

Friedman J H, Tukey J W. 1974. A projection pursuit algorithm for exploratory data analysis [J]. IEEE Transactions on Computers, 23(9): 881–890.

MacCallum R, Widaman K, Zhang S, et al. 1999. Sample size in factor analysis [J]. Psychological Method, 4: 84–99

StatSoft Inc. 2011. Electronic Statistics Textbook [EB]. Tulsa (http://www.statsoft.com/textbook ) .

Water quality comprehensive evaluation and prediction of the Yangtze River applying projection pursuit clustering technique and its positive analysis

LOU Wen-gao1,2, XIONG Pin2
(1. Shanghai Business School, Shanghai 200235, China; 2. School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)

According to the environmental quality standards for surface water and the measured data of eight indexes describing surface-water quality of the 103 government-control sections of the Yangtze River during the years from 2006 to 2010, the water quality evaluation model applying projection pursuit clustering (PPC) technique was established in this paper. The cases study results show that the water quality on the control sections is quite good, the type Ⅰ～Ⅲ taking up 92.82%, of which typeⅠ and type Ⅱ taking up 62.52% and 20.58%, respectively. The water quality in upper region is better than that in the downstream. The water pollution caused by Hg, petroleum, volatile phenol and NH3-N is serious in the chemical-industry developed areas, and the water quality is type Ⅴ. Comparison with that in year 2009, the water pollution in year 2010 is more serious. The cutoff radius R value (CRRV) obviously determines the results of PPC model. The theoretical analyses and positive researches show that the strategy of taking the smaller CRRV (R=0.1Sz) or the larger CRRV (rmax≤R≤2p) is absolutely unreasonable and unfeasible, and the strategy of taking the moderate-suitable CRRV (rmax/5≤R≤rmax/3), however, is reasonable and effective.

the Yangtze River; water quality comprehensive evaluation; projection pursuit clustering (PPC) modelling; cutoff radius R value

X824；TP391

：A

：1674-9901(2014)05-0344-09

10.7515/JEE201405006

2014-07-13

上海高校知识服务平台“上海商贸服务业知识服务中心”建设项目；上海市重点学科“商务经济学”项目

熊 聘，E-mail: pinxiongcn@foxmail.com