角度传感器变形仿真研究
2014-07-01康宁民王焕功郑应强薛继明
康宁民, 王焕功, 郑应强, 薛继明
(第二炮兵装备研究院,北京100085)
角度传感器变形仿真研究
康宁民, 王焕功, 郑应强, 薛继明
(第二炮兵装备研究院,北京100085)
通过ANSYS有限元法分析一种高精度角度传感器圆环的应变,采用将传感器圆环的转动转化为ANSYS中重力方向转动的方法,重力方向的转动转化为重力加速度在X轴和Z轴两个方向上的三角函数分解,从0′~300′每隔30′就测量一次,最后用MATLAB曲线拟合工具箱拟合出角度与应变的拟合曲线图和一元二次方程。
有限元;角度传感器;曲线拟合
0 引言
某型号高精度角度传感器,靠检测图1中圆环的应变转化为角度的数值,这种复杂的机械结构通过传统的材料力学的知识是没有办法精确求解的,因为圆环靠自身重力变形产生应变,但是材料力学中的重力必须有作用点、大小和方向。大小和方向是可以确定的,重力是一种体力,作用点和重心在不规则的结构面前很难确定,而采用有限元方法却可以高精度地仿真出来,精度取决于模型的建立精度和单元网格的划分精度。MATLAB软件适合于数值处理,仿真出的工程数据用MATLAB曲线拟合工具箱进行一元二次方程的曲线拟合,可以得到我们需要的变形方程。
1 模型建立
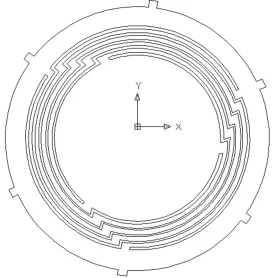
图1 CAD图
图1为通过扫描得到的AutoCAD里面的传感器圆环图形,线条不在同一平面内,在CAD中选中整个图形,右键在特性里面将所有曲线、直线的端点z坐标全都置0,使所有线都在同一平面。通过 DXF TO ANSYS软件将图 1导入ANSYS12.0软件中,如图2所示;在ANSYS中将图2的图形划分为11个封闭曲线,分别形成平面如图3所示,然后在preprocessor/modeling/operate/Booleans/glue/areas选择pick all,将所有11个平面粘成一个整体。
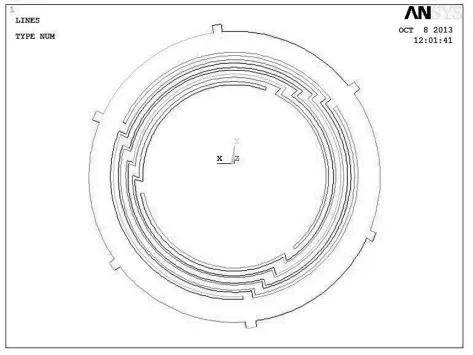
图2 ANSYS图
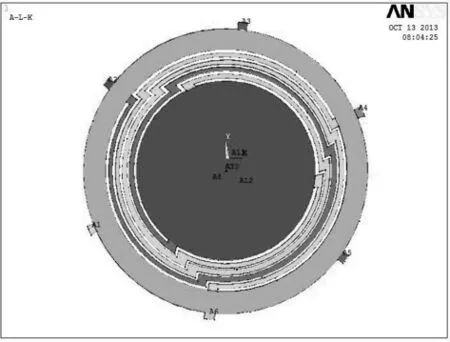
图3 形成平面
将图3保存为area.db文件。
2 网格划分
在网格划分前要先添加单元类型、实常数赋值以及材料弹性模量、泊松比和密度的赋值,单位采用mm/tone/ s单位制:
1)为保证精度和减少计算量,采用shell93单元,单元厚度1 mm:最好选择壳单元,采用实体单元需要网格划分足够密才能弥补精度的不足。
2)材料黄铜,杨氏弹性模量1.06E5MPa;泊松比0.324,密度8.5E-9t/mm3。
设置好参数后进入ANSYS前处理,选择meshing/ meshtool,在小窗口中选择size controls/globle/set,单元长度选择0.1,进行自由网格划分,选择所有面,网格划分如图4所示,将文件保存为mesh.db。

图4 划分网格
3 约束和载荷施加
在传感器实际使用当中圆环是随被测对象转动的,但是在ANSYS中图形转动困难,我们转化为重力方向转动。ANSYS中重力只能沿X、Y、Z三个轴向施加,而且是以惯性加速度的形式;如图4所示平面在XOY片面内,按实际情况我们将材料倾斜角度带来重力方向的变化分解为惯性力在X和Z两个方向的三角函数分量。
位移约束为圆环周围6个小突起的长方体全约束,如图5所示。
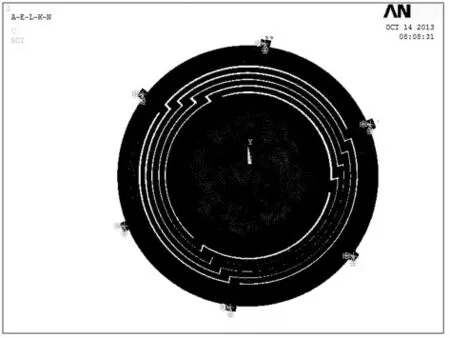
图5 位移约束
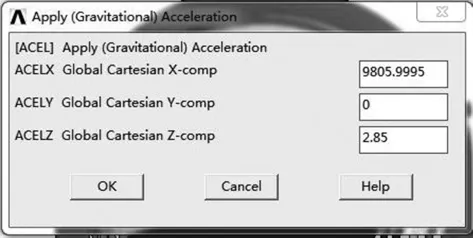
图6 倾角1′时重力载荷施加
从圆环转动1′开始,载荷施加如图6所示;重力g= 9806mm/s2,X轴和Z轴负向施加载荷的大小由下式三角函数给出:
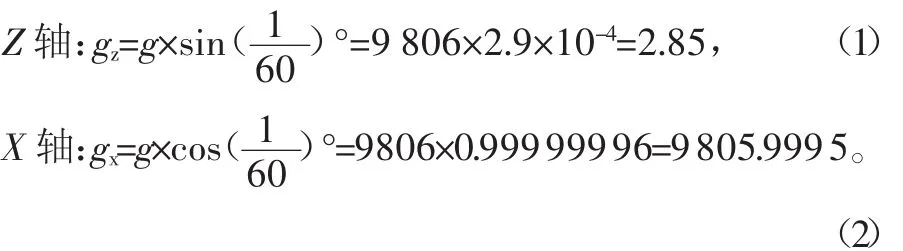
施加完后将文件存为constraint.db。
4 有限元分析及后处理
4.1 ANSYS有限元处理
Solution/solve/current LS运行完成后,进入后处理general postproc/plot result/deformed shape,得到结果如图7所示,最大位移DMX=0.029 966 mm。

图7 倾角1′时圆环Z轴最大位移
改变载荷,倾角0°时,如图8所示Z轴最大位移仍为DMX=0.029 966 mm。改变倾角10′、20′直到30′时Z轴最大位移DMX=0.029 967,以后每隔30′角度求解一次,直到300′,所得结果见表1。
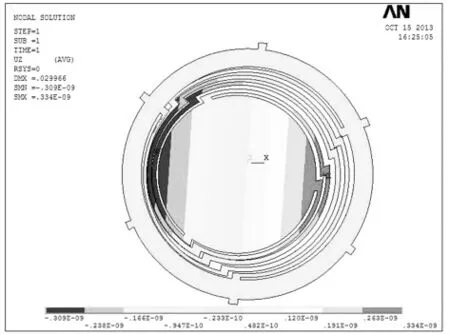
图8 倾角0°时圆环Z轴最大位移
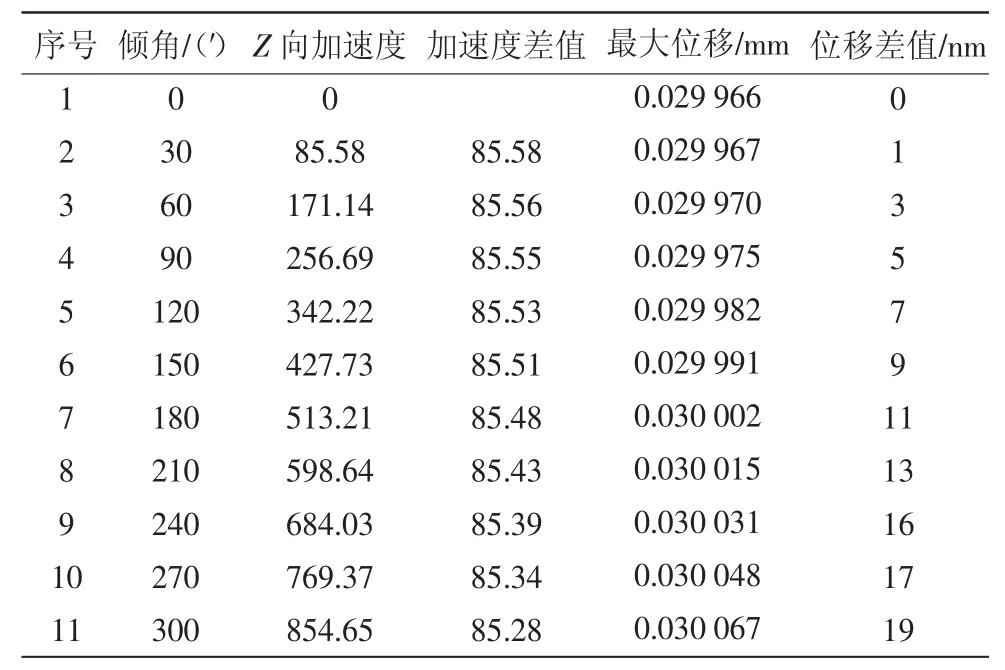
表1 倾角、Z向加速度和位移表
将表1中的数据输入MATLAB软件,用MATLAB软件画出倾角与最大位移的二维曲线图如图9所示。
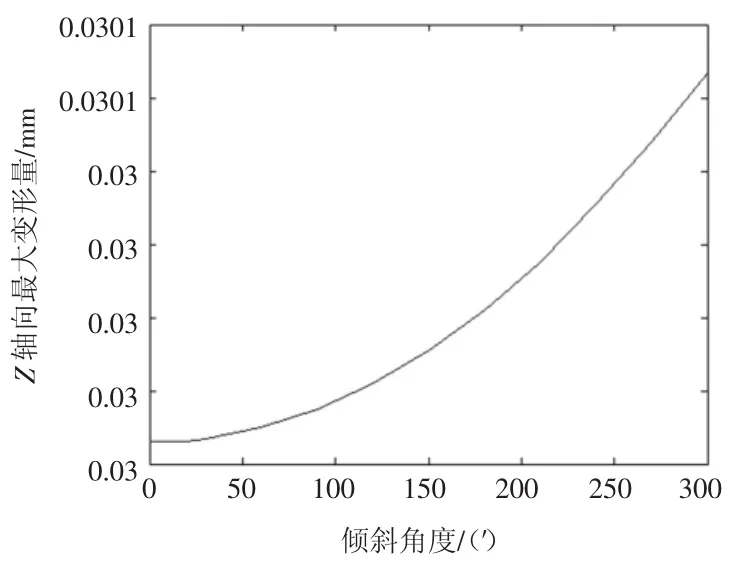
图9 倾斜角度与Z轴向最大位移曲线图
4.2 MATLAB曲线拟合

进入曲线拟合工具箱界面“Curve Fitting tool”
1)点击“Data”按钮,弹出“Data”窗口;
2)利用X data和Y data的下拉菜单读入数据x,y,修改数据集名“yxcurve”,然后点击“Create data set”按钮,退出“Data”窗口,返回工具箱界面,这时会自动画出数据集的点图;
3)点击“Fitting”按钮,弹出“Fitting”窗口;
4)点击“New fit”按钮,默认拟合项目名称,通过“Data set”下拉菜单选择数据集,然后通过下拉菜单“Type of fit”选择拟合曲线的类型,图9线型比较接近一元二次方程,但是选项里面没有,只能自己新建一个,选Custom Equations,点击“New”按钮,弹出自定义函数等式窗口,有“Linear Equations线性等式”和“General Equations构造等式”两种标签。选Custom Equations,点击“New”按钮,选择“General Equations”标签,输入函数类型y=a*x*x +b*x+c,设置参数a、b、c的上下限,然后点击OK,如图10所示。
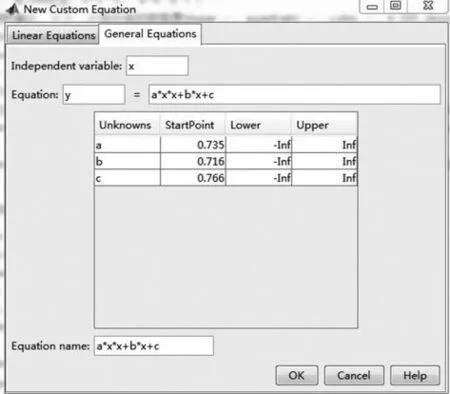
图10 拟合方程设置
在fitting界面点击apply,如图11所示。
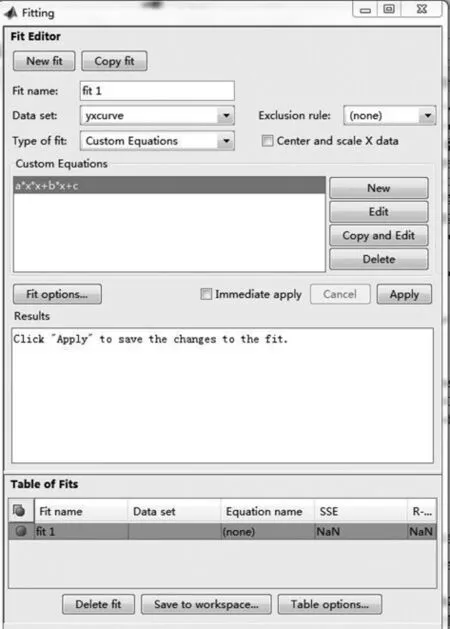
图11 fitting界面
拟合的曲线图如图10所示,运行结果为:
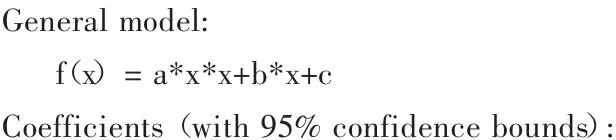

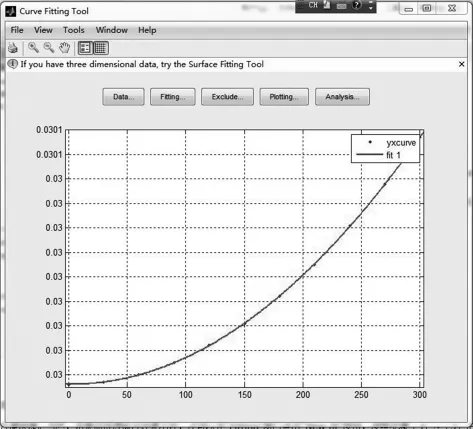
图10 一元二次曲线拟合图
5 结论
通过上述有限元分析和曲线拟合,我们可以看出:
1)基本上每隔30′,最大位移增加量就增加2nm,变形为非线性;
2)该变形可以用MATLAB曲线拟合工具箱得到其一元二次方程为:f(x)=1.137e-009*x*x-4.134e-009*x+0.02997;y为变形量单位mm;x为角度单位为分。可以为后续测量输出打下基础。
3)从结果可以看出误差平方和(SSE)和标准差RSME几乎为0,说明曲线拟合很好,一元二次方程类型选择很合适。
4)通过曲线拟合我们可以制造精度很高的角度测量传感器,不用受线形度的影响,测量范围得到很大提高,如果只在线形范围内我们的测量范围只有几分。
5)利用拟合曲形方程,我们只需要测量有限的点,其它点根据方程就可以算出,大大减少有限元分析的工作量。
[1] 余和五.二维高准确度水平传感器的研制[J].传感器技术,2001(11):27-32.
[2] 张洪才,何波.有限元分析—ANSYS13.0从入门到实战[M].北京:机械工业出版社,2011.
[3] 曾攀,雷丽萍,方刚.基于Ansys平台有限元分析手册—结构的建模与分析[M].北京:机械工业出版社,2011.
[4] 陈杰.Matlab宝典[M].北京:电子工业出版社,2007.
[5] 隋思涟,王岩.Matlab语言与工程数据分析[M].北京:清华大学出版社,2009.
(编辑:启 迪)
TP 391.7
A
1002-2333(2014)04-0131-03
康宁民(1972—),男,高级工程师,硕士学位,研究方向为机械设计和维修。
2014-01-27
