有限元分析中轴对称问题研究与应用

薛继明， 吴晓庆， 王焕功， 凌万胜

（第二炮兵装备研究院，北京100085）

有限元分析中轴对称问题研究与应用

薛继明， 吴晓庆， 王焕功， 凌万胜

（第二炮兵装备研究院，北京100085）

简要介绍了轴对称问题的概念和特征，列举了其基本方程和优点，将三维问题转化为二维问题，并且用一个正方形轴对称模型利用ANSYS软件建立四分之一模型，施加约束和载荷进行了有限元分析。通过与理论解的对比，发现随着网格的加密，有限元结果不断趋近于理论解，但在网格加密到一定程度1000×1000时，程序内存不够会导致崩溃，若充分利用模型的轴对称性能则可大大减少有限元分析的计算量。

有限元；轴对称；ANSYS

0 引言

在实际工程问题中，若结构的几何形状、约束条件以及所受载荷都对称于某一固定轴（称为对称轴），则结构在载荷作用下产生的位移、应变和应力必然也对称于该轴，这类问题称为轴对称问题，是弹性空间问题的一个特殊问题。这类问题的特点是物体为某一平面绕其中心轴旋转而形成的回转体。由于一般形状的轴对称物体，用弹性力学的解析方法进行应力计算，很难得到精确解，因此采用有限元法进行应力分析，在工程上十分需要，同时用有限元计算得到的数值解，近似程度也比较高。

1 力学参量与基本方程

1.1 力学参量

对于轴对称问题，通常采用柱坐标（r，θ，z）进行分析，如图1所示。

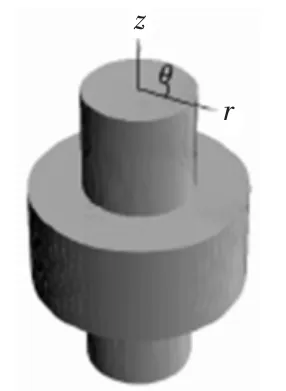
图1 轴对称问题示意图

以对称轴作为z轴，任意一点的位移、应变和应力都与θ无关，仅为r和z的函数。这样就将一个三维问题转化为二维问题，大大简化了有限元分析的工作量.

轴对称问题的力学参量：

由轴对称问题的力学参量可以看出，所有力学参量都是r和z的函数，与θ无关。

1.2 基本方程

1）平衡方程：

1.3 有限元离散

只需取出一个截面进行网格划分和分析，但这些单元都是环形单元，单元的结点力应理解为作用在单元结点所在的圆周上。

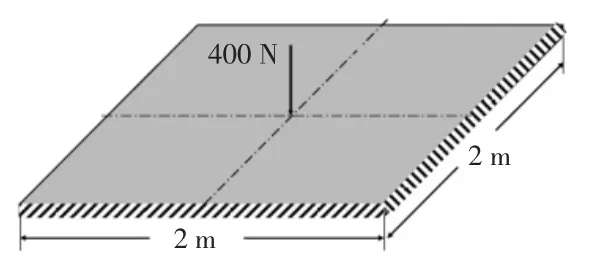
图2 正方形薄板示意图

2 对称性应用

正方形薄板边长l=2 m，厚度h= 0.01 m，四边固支。薄板弹性模量E= 200 GPa，泊松比=0.3。板中心受垂直集中载荷Q=400 N作用。试采用有限元法求板中心挠度并与理论解对比。

理论解：w=-0.005 6QL2/D，其中D=Eh3/（12（1-u2）），计算得：w=-0.000 489 216。

求解过程采用国际单位制。

1）设置软件。

（1）运行Ansys 12.0，输入文件名称，“ASYS”。

（2）Preference→structure→OK。

2）建立几何模型（取1/4进行分析）

（1）Preprocessor→Modeling→Create→Area→Rectangle→By Dimension。输入X向0，1；Y向0，1。

图3 几何模型

3）建立有限元模型。

（1）Preprocessor→Element Type→Elastic 4 node shell 63。

（2）Preprocessor→realconstant→Add→输入厚度0.01。

（3）Preprocessor→Material Props→Material Models→structural→Linear→Elastic→Isotropic→输入杨氏模量200e9，泊松比0.3。

图4 模型mesh图

（4）Preprocessor→Meshing→Mesh tool→set，选择面，点击Global，输入单元数目2（首先划分为2×2）。

4）施加载荷：（1）Solution→define Loads→Apply→Structural→disp-lacement→on line→点击外侧两个边，施加All DOF的约束。（2）Solution→define Loads→Apply→ Structural→disp-lacement→symmetay B.C.→on line→点击两个对称边，施加对称约束。（3）Solution→defineLoads→Apply→Structural→Force→on Keypoint，点击后（0，0）位置关键点，输入FZ，-100。

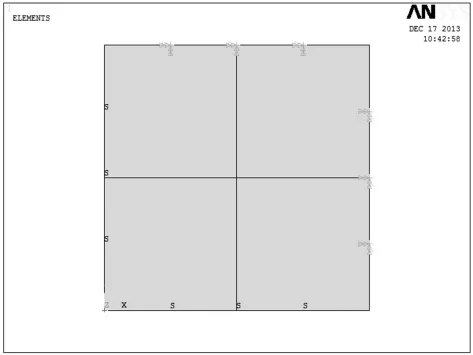
图5 约束边界条件

5）求解。Solve→Current LS。

6）后处理：General Postproc→read results→last set。General Postproc→Plot Results→Deformed Shape，可以看到显示结果 UZ。General Postproc→List Results→Nodalsolution→Nodal DOF→UZ。

图6 后处理结果

7）采用更小的单元求解。

（1）Preprocessor→Meshing→Mesh tool→set，选择面，点击Global，输入单元数目8（首先划分为8×8）。

（2）求解。Solve→Current LS。

（3）后处理。General Postproc→read results→last set。General Postproc→Plot Results→Deformed Shape，可以看到显示结果UZ。

General Postproc→List Results→Nodalsolution→Nodal DOF→UZ，得到UZ=-0.49388E-03。

采用16×16后，UZ=-0.49135E-03；采用100×100后，UZ=-0.49031E-03。

图7 8×8网格图

图8 8×8后处理结果

图9 100×100后处理结果

3 结语

通过上述有限元分析我们可以看到

1）随着网格越来越小，有限元分析应变UZ越来越接近理论值，所以有限元本质上就是微观世界的一种近似模拟；

2）利用结构轴对称性，可以简化模型的建立；

3）利用结构轴对称性可以大量减少有限元分析的工作量，在本次分析中当网格划分到1000×1000时，意味着有100万个单元，即式（1）到式（4）的矩阵方程至少要计算100万次，4G内存的计算机已经计算不了这么庞大的矩阵运算导致程序崩溃，若不用对称性，计算量至少要增大4倍，在500×500时计算机程序就会崩溃。

4）在有限元分析中首先要观察模型是否对称，采用对称约束在计算机硬件和模型大小一定的情况下能大大提高有限元分析的精度。

［1］ 商跃进，王红.有限元原理与ANSYS实践［M］.北京：清华大学出版社，2012.

［2］ 王焕功，康宁民，郑应强.车架静动力学分析［J］.科技研究，2012（5）：41-43.

［3］ 曾攀.有限元分析与应用［M］.北京：清华大学出版社，2004.

（编辑：立 明）

Finite Element Analysis and Application of Axisymmetric Problems

XUE Jiming,WU Xiaoqing,WANG Huangong,LING Wansheng
（Second Artillery Equipment Research Institute,Beijing 100085,China）

The concept and characteristics of axisymmetric problems are introduced,its basic equations and advantages are cited.The three-dimensional problem is transformed into a two-dimensional problem,and a quarter model is built using a square axisymmetric model in ANSYS software.The load and constraints are imposed on the quarter model to carry out finite element analysis in ANSYS.It is found that the results of the finite element trends toward to the theoretical solution with the increased mesh density.When the mesh density is 1000×1000,the program may lead to insufficient memory,so the axisymmetric model can greatly reduce the amount of computations in finite element analysis.

finite element;axisymmetric;ANSYS

TP 391.7

A

1002－2333（2014）04－0126－03

薛继明（1971—），男，高级工程师，硕士，研究方向为机电控制。

2014-01-10