改进的TRUST方法在航磁数据线性特征增强中的应用

耿美霞，黄大年，杨庆节

吉林大学地球探测科学与技术学院，长春 130026

改进的TRUST方法在航磁数据线性特征增强中的应用

耿美霞，黄大年，杨庆节

吉林大学地球探测科学与技术学院，长春 130026

基于各向异性扩散滤波的TRUST方法对航磁数据线性特征趋势增强时，未考虑数据光滑区域与异常边缘区域的区别，在光滑区域扩散持续进行，导致光滑区域产生许多虚假小异常。为此，提出一种改进的TRUST方法。该方法对TRUST方法中扩散张量的特征值通过引入相干性的办法进行了重新构造，使其能够正确识别光滑区域和异常边缘区域，并自动降低光滑区域的扩散速率，从而避免滤波过程中虚假异常的产生。在模型试验中，将该方法与TRUST方法处理结果进行了对比。结果显示，采用改进后的TRUST方法，不仅使航磁数据图上“串珠状”走样现象被消除，而且光滑区域的低振幅信息也被很好地保存。最后应用此方法对某地区的航磁数据进行趋势增强滤波，证实了该方法的实用性。

航磁数据；串珠状走样；趋势增强；TRUST方法

0 引言

地球物理数据处理往往要求数据是间隔均匀的网格数据，因此需要采用合理的网格化插值方法对原始测量数据进行网格化[1]。网格数据的质量直接影响后期数据处理以及解释图件的质量和可靠性。然而在航空数据采集中，测线之间的距离往往比测点之间的距离大很多，使得测量数据的不均匀性非常严重。这种密度显著不均匀的数据被称为测线型数据，对测线型数据网格化，常常会带来假异常[1]。例如，当线性异常的趋势方向与测线方向的夹角为锐角时，网格化后会出现“串珠状”假异常，并且夹角越小，这种假异常现象越明显。“串珠状”假异常不仅降低了航磁数据图形光滑度，还使本应明显的线性异常特征变成了小异常体特征，给后续处理和解释工作带来不便，甚至导致错误的解释。因此，为了满足当前高精度航空物探数据处理和解释的需要，保持原始测量信息的同时需要消除或减弱“串珠状”假异常现象，这已成为一个不能回避的问题。

大量研究[2-5]表明，无论是采用最小曲率、Akima插值还是双三次样条插值等方法，都会产生“串珠状”假异常现象，即“串珠状”假异常与常规网格化方法无关，而是由于测线间采样不足导致的短波长特征空间混叠效应而产生的。往往当测线间距大于或等于异常宽度的一半时，就会出现这种现象，并且异常走向与测线夹角越小，“串珠状”假异常越明显。前人研究[6-9]表明，使用最小曲率网格化过程中，用实际测量梯度数据代替计算得到的梯度数据，在一定程度上能够增强航磁数据中的线性特征，提高异常分辨率。但由于测量设备的限制，梯度数据并非总能获得。

由于“串珠状”走样问题的广泛存在，已经有很多学者对此进行了研究。Zhou[10]使用Radon变换的方法进行趋势增强，但是该方法只能对一个方向进行趋势增强。Sykes等[11]采用2-D Radon变换，通过在变换域中取阀值，对大于阀值的变换值作一定的增长，这样反演重建后的图像中相应的线性特征得到增强。但由于重磁图像线性特征的灰度相比于“背景”值并无特殊之处，阀值的选取较为困难。另外，该方法不能准确恢复原始图像的振幅，限制了其在高精度航磁数据处理中的应用。Hansen[12]采用各向异性克里金方法对数据进行网格化，由于该方法只能对一个固定的方向进行趋势增强，尚无法在有多个方向的趋势数据中应用。Fitzgerald等[13]沿着异常值方差最小的方向，从测线上抽取数据值，并将这些抽取的数据作为原始观测数据插入到测线之间，随后进行样条或最小曲率网格化；该方法需要确定一个接受度来判定特征是否为异常，网格化结果受接受度的影响非常大，并且对于走向与测线夹角小于45°的异常，处理效果不是很好。此外，Keating[14]采用最邻近分析法找出测线上的最大值和最小值，通过连接相邻测线上最邻近的最大值(或最小值)来确定插入测线间的数据，然后再进行网格化；该方法在线性特征走向与测线夹角比较大时能取得不错的趋势增强效果，但在构造复杂地区容易产生错误的线性趋势。

此外，基于偏微分方程尤其是各向异性扩散滤波方程的方法也已被应用到航磁数据趋势增强领域中[1, 15-16]。Smith等[16]成功地将各向异性扩散滤波方法应用到航磁数据趋势增强领域。该方法被称为TRUST(trends using structure)方法，它是在网格化后的数据上进行的，能自动对多个走向的趋势特征进行增强。然而TRUST方法未考虑数据光滑区域与异常边缘区域的区别，扩散在光滑区域持续进行，因而在光滑区域不可避免地产生虚假小异常。这种假异常在解析信号模图上会更加明显[16]，需要后续处理来消除。

笔者针对TRUST方法进行趋势增强时在光滑区域中产生虚假异常的缺点，基于相干性[17]重新构造新的特征值，从而构造新的扩散张量。新的特征值能够正确判断航磁异常数据中的光滑区域和异常边缘区域，以实现对不同的异常特征进行不同程度的扩散滤波，从而在消除“串珠状”构造的同时保护光滑区域的低振幅信息。

1 基于各向异性扩散滤波的TRUST趋势增强方法

基于偏微分方程的扩散滤波理论最初由Perona等[18]提出，并在数字图像处理领域中得到广泛应用。其构建的非线性扩散滤波模型为

其中：t为扩散时间；div为散度算子；g(·)为扩散滤波器的扩散系数，为一非负单调递减函数，且满足g(0)=1，g(∞)=1；u为t时刻的扩散滤波结果；u0表示t=0时的原始数据，作为该扩散方程的初始条件。

为了满足增强图像中各向异性纹理结构的需要，Weickert[19]通过对图像数据中各向异性结构的分析，将式(1)中的扩散系数变为张量，并构建了如下的张量型扩散模型[15]：

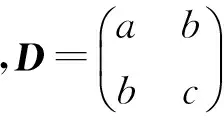
J0(uσ)=uσuσT=

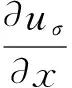
Jρ(uσ)=Gρ*(uσ

第一个特征向量v1=(cosφ,sinφ)T满足

‖

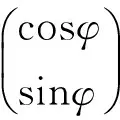
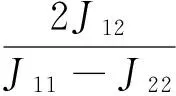
各向异性扩散张量D与结构张量J的特征向量相同，在Smith等[16]提出的TRUST方法中，其特征值为

式中，λ1和λ2又被称为扩散速率。D的分量分别为

在实际应用中，式(2)可以用有限差分方法求解，空间导数通常由中心差分代替[15]。式(2)的有限差分形式为

un+1=un+Δtdiv(Dn

其中：Δt为空间步长，通常情况下，只要Δt<0.25，式(11)在一定迭代次数内就是稳定的；un是u(x,y)在位置(x,y)处nΔt时刻的近似。由于扩散张量D在每次迭代过程中变化非常小，因此笔者选择在经过一定迭代次数后再重新计算一次D，这样可以大大提高该方法的计算效率。

2 改进的TRUST方法

观察式(9)可发现，特征值λ2没有考虑到光滑区域与边缘区域之间的差别，在相对光滑的区域滤波容易导致虚假异常的产生：在光滑区域，只要存在梯度各向异性，就会沿着梯度值较小的方向扩散，从而导致虚假异常的出现。

实际上，结构张量的特征值μ1和μ2包含了图像结构信息[17]。所以特征值μ1、μ2可以用来描述图像的局部结构特征：在光滑区域μ1≈μ2≈0；对于构造的边缘区域μ1≫μ2≈0；在拐角的边界区域有μ1>μ2≫0。由此定义相干性H[17]如下：

根据局部图像的相干性，笔者构造了新的特征值：

其中，C为常数。

扩散滤波的过程是将原始的图像数据，即航磁数据进行滤波。其在消除“串珠状”假异常的同时，不可避免地造成原始测点上数据的改动。这样的滤波处理违背了高精度航磁异常处理的原则[16]。一个防止原始测线数据被改动的简单方法，就是在迭代滤波过程中将这些测点数据固定不变。在实际应用中，另一个问题是迭代停止时间的选择。迭代次数过少，图像上的线性特征得不到足够的增强；而迭代次数过多不仅花费的计算时间较长，还会导致图像被过度平滑。因此，选择适当的迭代次数对最终趋势增强效果非常重要。根据笔者的试验结果，一般情况下，迭代次数取300～500，就能得到比较满意的趋势增强效果。

3 关于几个参数的意义和选择

在结构张量构造中有2个参数，σ和ρ。其中，参数σ被称为噪声尺度[16]。对原始数据处理前，先用噪声尺度为σ的高斯核对数据进行卷积，可以保证在进行求导计算时，尺度小于σ的数据不对导数计算产生影响，从而保证了求导过程的稳定性和可靠性。在选取参数σ时，根据航磁数据的噪声水平进行选择，才能达到预期的目的。根据笔者的试验结果，发现通常σ选择为1倍测线距左右时，能够得到较好的滤波效果。

参数ρ被称为综合尺度，它反映的是图像的纹理特征[16]。它的作用是对结构张量的方向进行滤波，进一步消除尺度规格小于ρ的噪声干扰。如果ρ的值过大，就会使滤波后的数据过度平滑，丢失原有信息。根据笔者的试验结果，通常ρ选择为1.5倍的测线距。这样能够保证连续出现在相邻2条测线上的“串珠”异常得到增强。

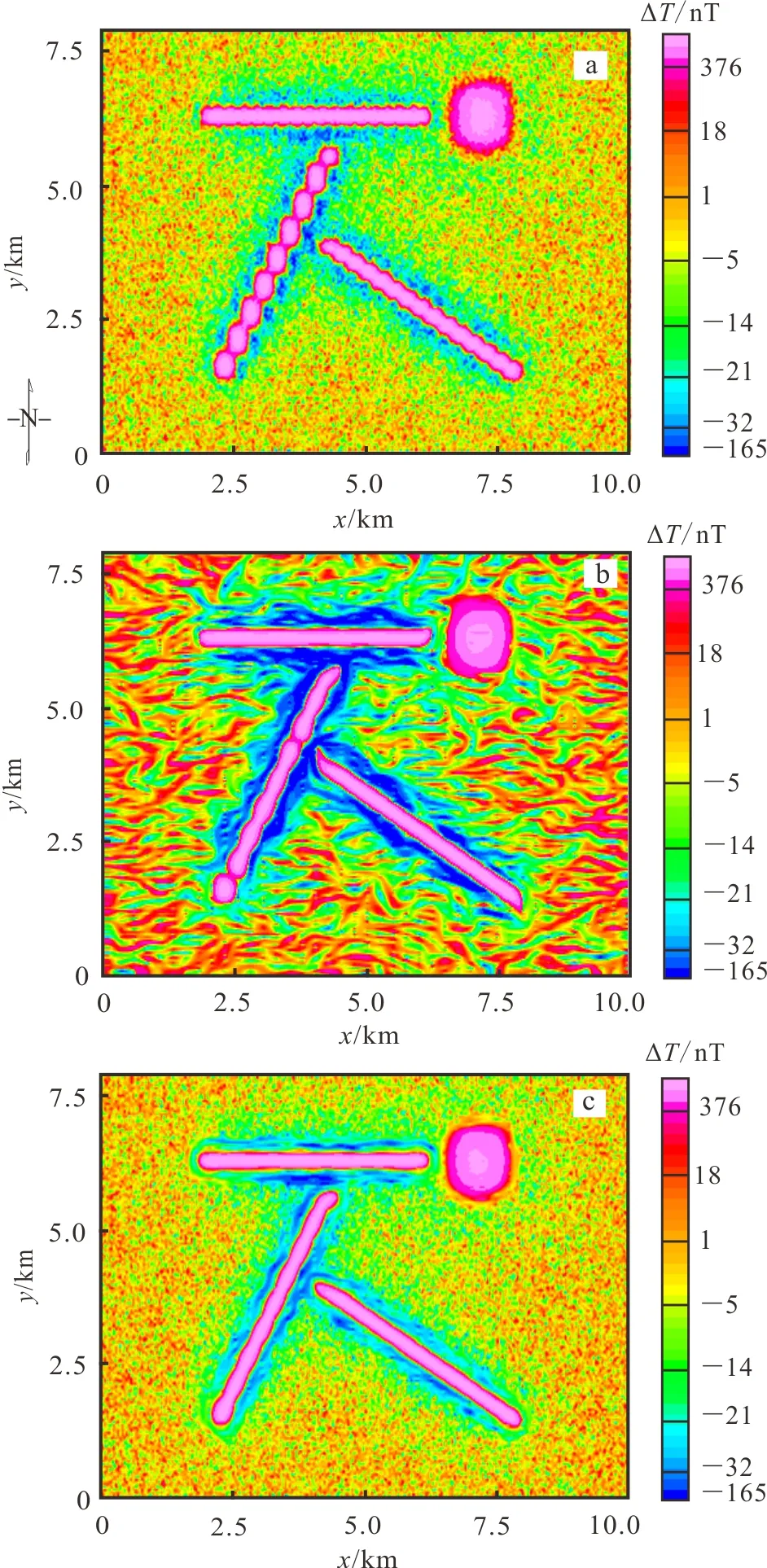
a.滤波前；b.TRUST方法滤波后；c.改进的TRUST方法滤波后。图1 趋势增强前后航磁异常(ΔT)图Fig.1 Application of the trend enhancement filter to the aeromagnetic data

4 模型计算与对比

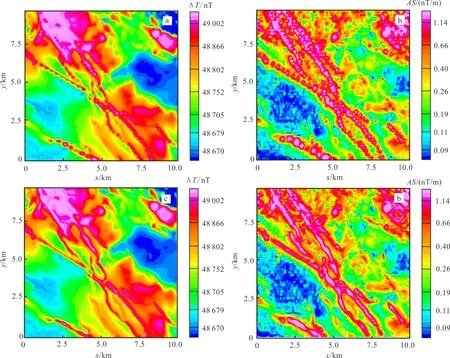
a.原始航测数据网格化后异常；b.原始异常解析信号模；c.经过改进的TRUST方法滤波后的航磁异常；d.经过改进的TRUST方法滤波后异常的解析信号模。AS=。图2 航测数据趋势增强前后异常和相应的解析信号模图Fig.2 Comparison of the original aeromagnetic data and the data after trend enhancement as well as the corresponding analytic signal maps

为了验证改进的TRUST方法消除“串珠状”假异常的有效性，笔者采用了含有高斯白噪声的组合磁性体模型对趋势增强效果进行检验。组合模型包括1个块状和3个不同走向的脉状体，磁化方向I0=75°，磁偏角A0=25°，磁化强度J=1 A/m。测线方向为南北方向。如图1a所示，3个脉状体与测线的夹角分别为30°，60°和90°。测线间距为 200 m，测线上测点间距为 10 m，在原始的测线数据中加入了8%的高斯白噪声。采用最小曲率方法对测线数据进行网格化，网格间距为 50 m。图1a 给出了网格化后的航磁异常。从图1a 可以看到：当线性磁异常与测线夹角为锐角时，网格化后异常呈现出“串珠状”假异常特征，并且，夹角越小，这种走样现象越严重；垂直于测线的线性磁异常以及块状磁异常，虽然没有出现走样现象，但是网格化后异常的边缘呈“锯齿状”，影响了图像的光滑性。

图1b显示的是经过TRUST方法扩散滤波后的航磁异常图。迭代次数为300。可以看到：经过TRUST方法滤波后，与测线夹角为锐角的线性趋势特征得到增强，“串珠状”假异常基本被消除；同时，块状异常和与测线垂直的线性异常边缘的“锯齿”特征也被消除。然而，由于噪声的存在，滤波后光滑区域产生了大量小的假异常。此外沿测线方向也有少量的高频假异常产生。

图1c显示的是经过改进的TRUST方法扩散滤波后的航磁异常。迭代次数同样为300。可以看到：经过改进的TRUST方法滤波后，与测线夹角为锐角的线性趋势特征得到增强，“串珠状”假异常被完全消除；块状异常和与测线垂直的线性异常边缘的“锯齿”特征也被很好地消除。此外，由于改进的TRUST方法中扩散张量的特征值能够在相对平滑区域自动降低扩散速率，有效地保护了原始低振幅信息，从而避免了平滑区虚假小异常的产生。

5 实例分析

图2a 为某地区采集的航空磁异常数据，该地区存在大量的西北--东南走向的脉状磁性体。飞行测线距为 200 m，测点距为 17 m，测线方向为东西方向。采用最小曲率法对原始的航磁数据进行网格化，网格间距为 40 m。可以看到，图2a上存在明显的“串珠状”走样，并且与测线方向夹角越小，“串珠状”走样越明显。图2b 为该异常的解析信号模。解析信号模类似于航磁化极图，能够部分消除斜磁化影响，异常幅度大体反映了场源的相对磁性强度[20]，并且对异常体的边缘非常敏感，因此常被用来估计磁异常体的水平位置。在解析信号模(图2b)上，“串珠状”走样特征更加明显，给后续处理和解释工作带来不便，甚至可能导致错误的解释。

图2c 为图2a 中的数据经过改进后的TRUST方法滤波后的航磁异常图。迭代次数为300。可以看到，经过滤波之后，“串珠状”假异常被消除，同时线性特征也得到了增强。由于改进后的TRUST方法能够在光滑区域自动降低扩散速率，因此光滑区域的低振幅信息也被很好地保存下来。图2d 为图2c 的解析信号模，可以看到，“串珠状”走样特征也已被消除，使后期解释更加方便。

为了检验趋势增强前后航磁图上数据的变化，从图2a 上用沿某一线性趋势方向虚线标出的点提取数值，并将抽取的数据点构成一条剖面(图3)。经过300次迭代滤波后，该剖面数据再次显示在图3中。可以看到，滤波后剖面数据上的波峰抖动被消除，得到了一个相对光滑的长波长曲线。图3中五角星指示的峰值都是航空测线穿越的位置。由于在进行滤波运算的同时固定原始测点数据不变，所以滤波后原始测点上的数据被保存下来。

图3 滤波前后抽取的剖面数据对比Fig.3 Comparison of the original data on the ridge profile and the data after trend enhance

6 结束语

本文针对TRUST方法扩散张量特征值的选取不适合光滑区域滤波而导致虚假异常的缺点，引入图像相干性，重新构造了扩散张量的特征值。新的特征值能够正确区分航磁异常中的异常边缘和光滑区域，并在光滑区域自动降低扩散速率以便有效地保护低振幅信息，从而避免了假异常的产生。此外，为了保护原始测信息，本文算法在滤波过程中对原始测线上的数据点进行了约束保护，使得处理后的数据精度得到很大提高，在实际数据应用中取得了非常好的效果。

[1] 姚长利，庞旭林. 航磁数据线性特征增强滤波方法技术研究[C]//中国地球物理年会.北京：中国地球物理学会，2009：267. Yao Changli, Pang Xulin. Researeh on the Enhancement Trends of Magnetic Date[C]// Chinese Geophysics Society Annual Meeting. Beijing: Chinese Geophysical Society，2009: 267.

[2] Billings S, Richards D. Quality Control of Gridded Aeromagnetic Data[J]. Exploration Geophysics, 2000, 31 (4): 611-616.

[3] 李丽丽，杜晓娟，马国庆. 改进的局部波数法及其在磁场数据解释中的应用[J]. 吉林大学学报：地球科学版，2012，42(4): 1179-1185. Li Lili, Du Xiaojuan, Ma Guoqing. Improved Local Wave Number Methods in Interpretation of Magnetic Fields[J]. Journal of Jilin University: Earth Science Edition, 2012, 42(4): 1179-1185.

[4] 曾昭发，吴燕冈，郝立波，等. 基于泊松定理的重磁异常分析方法及应用[J]. 吉林大学学报：地球科学版，2006，36(2)： 279-283. Zeng Zhaofa, Wu Yangang, Hao Libo, et al. The Poisson’s Theorem Based Analysis Method and Application of Magnetic and Gravity Anomalies[J]. Journal of Jilin University: Earth Science Edition, 2006, 36(2): 279-283.

[5] 方东红，曾昭发，陈家林. 基于小波分析的重磁数据求导方法及应用[J]. 吉林大学学报：地球科学版，2008，38(6)：1049-1054. Fang Donghong, Zeng Zhaofa, Chen Jialin. The Derivatives Calculation Based on Wavelet Analysis of G/M Data and Its Application[J]. Journal of Jilin University: Earth Science Edition, 2008, 38(6): 1049-1054.

[6] Marcotte D L, Hardwick C D, Lemieux J M, et al. Aeromagnetic Gradiometry Methods: A Study Using Real Data[C]//60th Annual International Meeting. SEG: [s.n.], 1990:584-586.

[7] Cowan D R, Baigent M, Cowan S. Aeromagnetic Gradiometers: A Perspective[J]. Exploration Geophysics, 1995, 26: 241-246.

[8] McMullan S R, McLellan W H, Koosimile D I. Three Dimensional Aeromagnetics[J]. Preview, 1995, 57: 83-91.

[9] Hardwick C. Gradient-Enhanced Total Feld Gridding[C]// 69th Annual International Meeting.SEG: [s.n.], 1999:381-384.

[10] Zhou Y X. Radon Transform Application to the Im-proved Dridding of Airborne Geophysical Survey Data[J]. Geophysical Prospecting, 1993, 41: 459-494.

[11] Sykes M P, Das U C. Directional Filtering for Linear Feature Enhancement in Geophysical Maps[J]. Geophysics, 2000, 65: 1758-1768.

[12] Hansen R O. Interpretive Gridding by Anisotropic Kriging[J]. Geophysics, 1993, 58: 1491-1497.

[13] Fitzgerald D, Yassi N, Dart P. A Case Study on Geophysical Gridding Techniques: Intrepid Perspective[J]. Exploration Geophysics, 1997, 28: 204-208.

[14] Keating P. Automated Trend Reinforcement of Aero-magnetic Data[J]. Geophysical Prospecting, 1997, 45: 521-534.

[15] 孙夕平，杜世通，汤磊. 相干增强各向异性扩散滤波技术[J].石油地球物理勘探，2004，39(6)：651-655. Sun Xiping, Du Shitong, Tang Lei. Coherent-Enhancing Anisotropic Diffusion Filtering Technique[J]. Oil Geophysical Prospecting, 2004, 39(6): 651-655.

[16] Smith R S, O’Connell M D. Interpolation and Grid-ding of Aliased Geophysical Data Using Constrained Anisotropic Diffusion to Enhance Trends[J]. Geophysics, 2005, 70(5): 121-127.

[17] 王大凯，侯榆青，彭进业. 图像处理的偏微分方程方法[M]. 北京：科学出版社，2008. Wang Dakai, Hou Yuqing, Peng Jinye. Partial Differential Equation in Image Processing[M]. Beijing: Science Press, 2008.

[18] Perona P, Malik J. Scale Space and Edge Detection Using Anisotropic Diffusion[J]. IEEE Trans Pattern Anal Mach Intell, 1990, 12: 629-639.

[19] Weickert J. Anisotropic Diffusion in Image Pro-cessing[M]. Stuttgart: Teubner,1998.

[20] 骆遥，王明，罗锋，等. 重磁场二维希尔伯特变换：直接解析信号解释方法[J]. 地球物理学报，2011，54(7)：1912-1920. Luo Yao, Wang Ming, Luo Feng，et al. Direct Analytic Signal Interpretation of Potential Field Data Using 2-D Hilbert Transform[J]. Chinese Journal of Geophysics, 2011, 54(7): 1912-1920.

Application of Improved TRUST Method in Enhancing Linear Trends of Aeromagnetic Data

Geng Meixia，Huang Danian，Yang Qingjie

College of GeoExploration Science and Technology, Jilin University, Changchun 130026, China

As for the enhancement of linear Trends, the TRUST method proposed by Smith and O’Connell does not consider the distinctions between the smooth area and other image features. The diffusion is carried on in smooth area and thus inevitably produces artifacts. An improved TRUST method was proposed. The eigenvalues of the structure matrix are reconstructed，so that the method only diffuses the image in specific areas where strong anisotropy is detected. This method is tested on both synthetic and field data sets. The results indicate that the method can be used efficiently to enhance linear structure locally in multiple directions. We have also compared the proposed method with the TRUST method by applying them to the synthetic data set. The results demonstrate that the proposed method can produce better effect with fewer artifacts.

aeromagnetic data；boudinage；enhancement of trends；TRUST method

2014-03-04

国家“863”计划项目(2014AA06A613)；吉林大学研究生创新基金资助项目(2014066)

耿美霞(1986--)，女，博士研究生，主要从事航空重磁数据处理和反演方面的研究，E-mail:gengmeixia@126.com

黄大年(1958--)，男，教授，博士生导师，国家千人计划特聘专家，主要从事移动平台探测数据处理与解释及一体化软件平台开发，E-mail:dnhuang@jlu.edu.cn。

10.13278/j.cnki.jjuese.201404301.

10.13278/j.cnki.jjuese.201404301

P631.2

A

耿美霞，黄大年，杨庆节.改进的TRUST方法在航磁数据线性特征增强中的应用.吉林大学学报:地球科学版,2014,44(4):1333-1339.

Geng Meixia，Huang Danian，Yang Qingjie.Application of Improved TRUST Method in Enhancing Linear Trends of Aeromagnetic Data.Journal of Jilin University:Earth Science Edition,2014,44(4):1333-1339.doi:10.13278/j.cnki.jjuese.201404301.