裂缝性地层钻井液漏失模型及漏失规律

贾利春，陈 勉，侯 冰，孙 振，金 衍

（1. 中国石油大学（北京）油气资源与探测国家重点实验室；2. 中国石化江苏油田分公司石油工程技术研究院）

裂缝性地层钻井液漏失模型及漏失规律

贾利春1，陈 勉1，侯 冰1，孙 振2，金 衍1

（1. 中国石油大学（北京）油气资源与探测国家重点实验室；2. 中国石化江苏油田分公司石油工程技术研究院）

针对裂缝性地层钻井作业时的钻井液漏失问题，采用幂律模式钻井液，将地层中裂缝看作任意倾角、可变形、裂缝面粗糙且存在滤失的二维单条裂缝模型，引入裂缝力学开度和裂缝迂曲度参数表征裂缝面粗糙度对钻井液漏失规律的影响，推导了钻井液漏失模型，并基于该模型分析了钻井液漏失规律。研究结果表明，幂律模式钻井液的剪切稀释性会造成漏失初始阶段漏失速率的升高；钻井液漏失速率随裂缝迂曲度变大而减小，随着裂缝开度增加裂缝迂曲度对钻井液漏失速率的影响降低；初始裂缝开度、裂缝倾角、裂缝面积、裂缝长度越大，钻井液漏失速率越大；矩形裂缝的钻井液漏失速率低于正方形裂缝；裂缝面滤失综合系数越大，钻井液漏失速率越高；井眼与裂缝相交于裂缝中心位置时钻井液漏失速率最高；随着井底压差增大，钻井液漏失速率明显升高；裂缝法向刚度越高，钻井液漏失速率越小。图9表1参29

裂缝性地层；钻井液漏失；裂缝；幂律流体；漏失模型；漏失速率

0 引言

在裂缝性地层中进行钻井作业时通常会有大量钻井液漏失到裂缝中，造成钻井成本增加和其他井下复杂事故[1]。井漏是目前钻井作业中的技术难题之一，通过分析钻井液漏失数据、研究钻井液漏失规律，可以判断和评价地层中裂缝发育特征，为后续堵漏作业提供所需参数[1-3]。

裂缝性地层中钻井液漏失的本质是流体通过井眼流进裂缝。地层中的裂缝表面不规则，裂缝面粗糙度对流经裂缝的流体具有很大影响。裂缝面通常具有渗透性，钻井液漏失到裂缝中后会通过裂缝面滤失到地层基质中，因此裂缝面滤失性会影响钻井液漏失规律。

近20年来，众多研究者提出了多种钻井液漏失模型以定量分析钻井液漏失规律。Lietard O等[4]提出了单条光滑裂缝条件下的宾汉模式钻井液漏失模型。Lavtov A等[5-8]对钻井液漏失机理进行了深入研究。Majidi R等[9-11]建立了光滑径向裂缝条件下赫巴模式钻井液漏失模型。Ozdemirtas M等[12-13]根据Reynolds方程提出了考虑分形裂缝粗糙度的二维钻井液漏失模型，并通过室内漏失模拟实验验证了模型正确性。Shahri M P等[14]建立了二维任意倾角裂缝条件下赫巴模式钻井液漏失模型，但是未考虑裂缝表面粗糙度的影响。李大奇[15]建立了一维单条裂缝和二维、三维离散裂缝网络中赫巴模式钻井液漏失模型。上述研究者在建立钻井液漏失模型时，没有综合考虑裂缝面粗糙度、裂缝面滤失性、钻井液流变性等对钻井液漏失规律的影响。关于粗糙裂缝内流体流动规律，已有研究者进行了深入研究，但主要针对牛顿流体[16-22]。此外，仅有Lavtov A等[6]和李大奇[15]建立的模型中考虑了裂缝面滤失性对钻井液漏失规律的影响。

本文采用幂律模式钻井液，建立考虑裂缝面粗糙度及滤失性的二维单条任意倾角裂缝钻井液漏失模型。基于该模型分析裂缝面迂曲度、钻井液流变参数、裂缝几何参数、裂缝面滤失性等对钻井液漏失速率的影响规律。

1 裂缝表征

目前，常采用分形法模拟裂缝面的粗糙特性[8,12,17-19]。分形维数D和Hurst指数H是描述分形特征的两个重要参数，通常D=3-H。图1给出了不同分形维数下的裂缝面，可以看出，Hurst指数越小，裂缝面越粗糙。

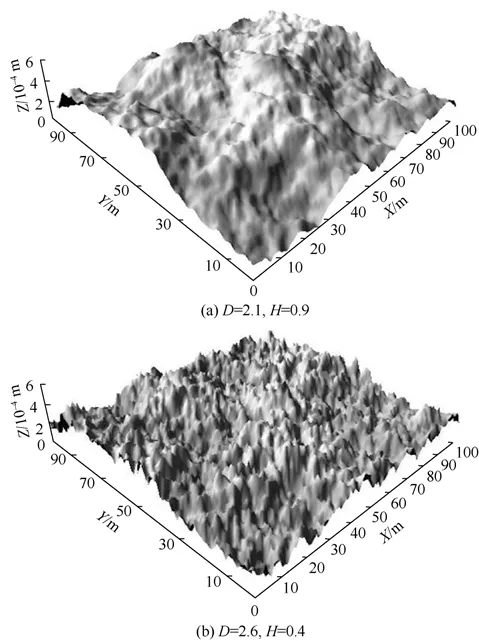
图1 不同分形维数下裂缝面示例

目前部分钻井液漏失模型中通过分形方法表征裂缝面粗糙度，但只有在裂缝开度满足指数变形规律的前提下，才能在钻井液漏失控制方程中体现裂缝面粗糙度对钻井液漏失规律的影响[8,12,15]，此外，这些模型不能体现裂缝面粗糙度对裂缝开度的影响。因此，本文采用裂缝迂曲度来表征裂缝面粗糙特性。

前人在研究缝内流体流动规律时，常把裂缝简化为平行板模型[16]，使得钻井液漏失规律分析结果存在误差。为修正平行板模型，研究者提出了多种裂缝开度定义，其中力学开度和水力开度是分析缝内流体运动规律的重要参数[20-21]。在岩体水力学或地下水渗流研究范围内，水力开度等于力学开度，所以在分析缝内流体流动时只采用水力开度。但裂缝面粗糙度的变化会引起力学开度的变化，使得两者不相等[22-27]。因此，有研究者利用裂缝迂曲度将两者联系起来，以正确表征裂缝面粗糙度对缝内流体流动规律的影响。力学开度、水力开度与裂缝迂曲度间关系[28]为：

（1）式中，δ为裂缝迂曲度，地层中天然裂缝迂曲度为1～2。当δ=1时，裂缝为光滑平行板裂缝。由于裂缝迂曲度可以采用分形方法表征，因此适用性更强[29]。

本文在钻井液漏失控制方程中引入力学开度和裂缝面迂曲度，以表征裂缝面粗糙度对钻井液漏失规律的影响。

2 钻井液漏失模型

假设地层中存在1条任意倾角的矩形裂缝（见图2），裂缝面具有渗透性。沿裂缝面建立直角坐标系，x轴为水平方向，沿着裂缝走向；y轴沿着裂缝倾角方向，裂缝倾角为α。沿x轴和y轴方向的裂缝长度分别为Lx和Ly，Lx/Ly值可以表征裂缝面的形状。考虑3种井眼与裂缝面相交位置，分别为裂缝中心、裂缝边界中心和裂缝角点。

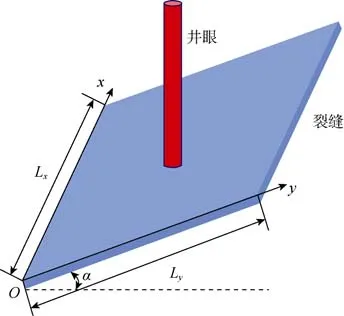
图2 钻井液漏失裂缝模型示意图

该模型中，井眼钻遇裂缝前，裂缝内初始压力为pi，假设缝内流体与井眼内钻井液具有相同流变性和性能。在t=0时，井眼与裂缝面相交。假设在井眼与裂缝面相交后，钻井液立即进入裂缝且缝内压力上升至与井内压力pw相等。一般情况下可将钻井液看作不可压缩的非牛顿流体，具有剪切稀释特性。本文假设钻井液为幂律流体，其流变方程[24]为：

2.1 裂缝变形方程

假设裂缝可变形，裂缝开度随缝内压力的波动而变化。井眼与裂缝相交后，钻井液进入裂缝，造成缝内压力的变化，最终引起裂缝开度的变化。在本文建立的钻井液漏失模型中，假设裂缝变形规律满足线性变形方程，即某一点的裂缝开度与缝内压力呈线性关系[11]：

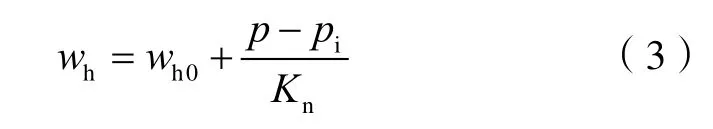
2.2 钻井液漏失控制方程

由质量守恒定律和Reynolds方程可得到二维单条裂缝中钻井液流动的控制方程：

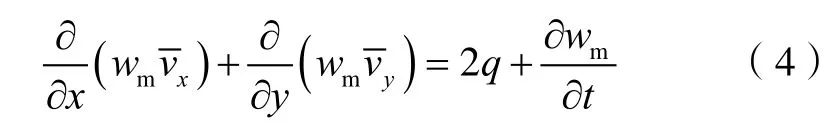
（4）式中q表示裂缝面滤失引起的缝内钻井液变化，可由Carter方程[6,15]得到：

将（1）、（3）、（5）、（6）、（7）式代入（4）式，可得二维单条任意倾角裂缝中幂律模式钻井液漏失控制方程：

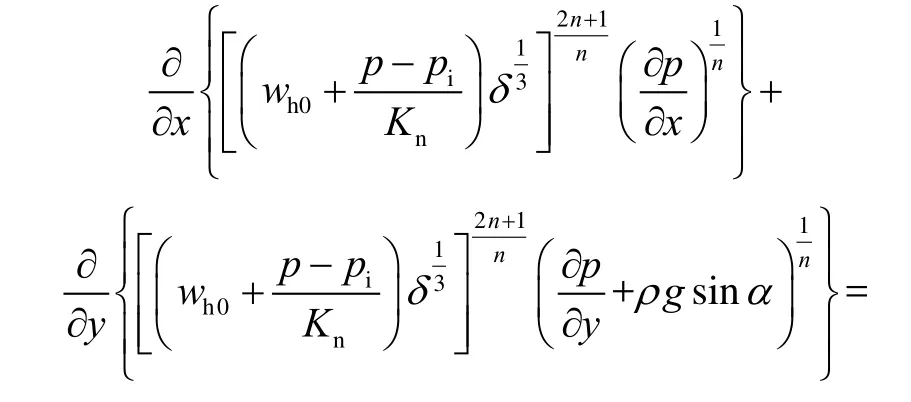
3 钻井液漏失规律

利用上述钻井液漏失模型可以分析各种因素对钻井液漏失速率的影响规律，包括钻井液流变参数、裂缝迂曲度、裂缝几何参数及裂缝面滤失性等。表1为钻井液漏失规律分析中所采用的基本参数。在分析某一特定参数对钻井液漏失速率的影响时，假设其他参数保持不变。除了研究井眼与裂缝相交位置对钻井液漏失速率影响外，井眼与裂缝相交位置均在裂缝中心。井底压差表示井内压力与缝内初始压力的差值，通过改变井内压力改变井底压差。

表1 钻井液漏失规律分析中基本参数

3.1 钻井液流变参数

钻井液流变参数影响缝内流体流动规律，是钻井液漏失速率的重要影响因素。分析了幂律模式钻井液流动特性指数、稠度系数对钻井液漏失速率的影响（见图3）。

由图3a可知，随着钻井液流动特性指数的减小，钻井液漏失速率峰值逐渐变大，且漏失速率曲线下降斜率增大，尤其是在曲线末段。这是由于流动特性指数越小，钻井液剪切稀释效应越明显，缝内钻井液流动阻力也越小，从而使钻井液漏失速率变大。

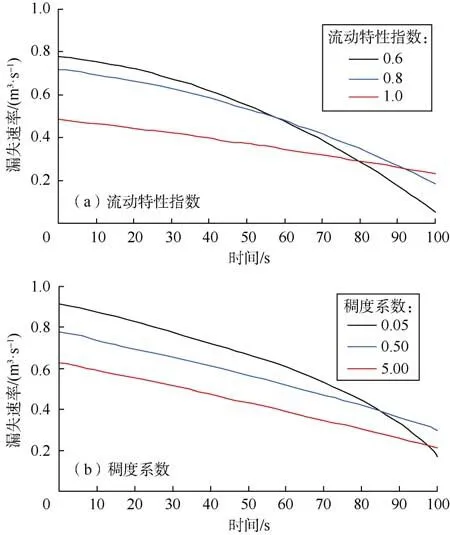
图3 钻井液流变参数对钻井液漏失速率的影响

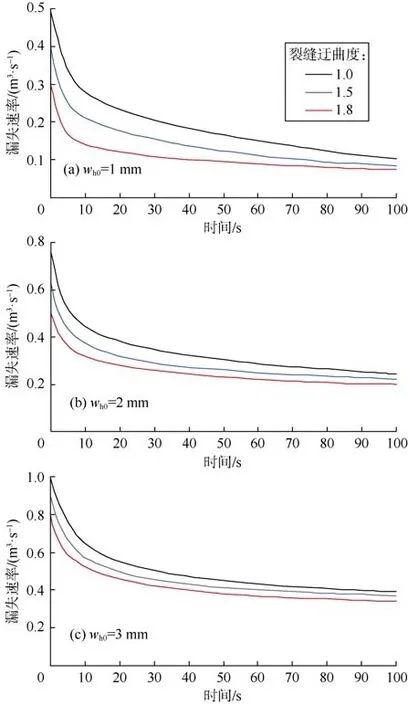
图4 裂缝迂曲度对钻井液漏失速率的影响

由图3b可知，钻井液稠度系数越高，漏失速率峰值越小。这是由于较大的稠度系数会造成钻井液塑性黏度较大，缝内钻井液流动阻力也较大。

3.2 裂缝迂曲度

采用裂缝迂曲度表征裂缝面粗糙度对钻井液漏失规律的影响。图4为不同初始裂缝开度下裂缝迂曲度对钻井液漏失速率的影响，可以看出：在初始裂缝开度相同的情况下，裂缝迂曲度越高，钻井液漏失速率越小；在漏失初始阶段，漏失速率快速降低，而后逐渐降低至漏失末段的稳定状态；随着初始裂缝开度的增大，裂缝迂曲度对漏失速率的影响程度逐渐减小，且漏失速率峰值明显升高。因此，当初始裂缝开度足够大时，可以将裂缝简化为光滑平行板，初始裂缝开度较小时，则不能忽略裂缝面粗糙度对钻井液漏失速率的影响。

3.3 裂缝几何参数

分别对裂缝倾角、初始裂缝开度、裂缝面积、裂缝长度和裂缝形状对钻井液漏失速率的影响进行了分析（见图5）。

由图5a可知，随着裂缝倾角的增加，钻井液漏失速率及其峰值均逐渐变大，漏失速率曲线下降斜率也逐渐变大。裂缝倾角对钻井液漏失速率的影响实质上反映了重力对缝内钻井液流动的影响，对于水平裂缝，重力的影响可以忽略，而对于倾斜裂缝，须考虑重力对钻井液漏失的影响。

由图5b可知，初始裂缝开度越大，钻井液漏失速率越大。由（3）式可知，在相同缝内压力条件下，初始裂缝开度变大会造成裂缝开度变大，为钻井液漏失提供更大通道。

由图5c可知，不同裂缝面积条件下，漏失初始阶段钻井液漏失速率相同，之后漏失速率曲线会出现差异。裂缝面积越小，漏失末段钻井液漏失速率越低。

应该争取更多的“常规报告”（regular或invited lecture）．“常规报告”的入选在很大程度上靠报告者在学术圈的知名度和研究工作的水平．现在常规报告的人选已经确定，需要常规报告的入选者今后围绕报告主题精心准备．

保持x轴方向裂缝长度不变而改变y轴方向裂缝长度，研究裂缝长度对钻井液漏失规律的影响。由图5d可知：不同裂缝长度条件下，漏失初始阶段的漏失速率相同，而之后漏失速率曲线下降程度不同；裂缝长度越小，漏失末段的钻井液漏失速率越低。

保持裂缝面积不变，用Lx/Ly表征裂缝面的形状。图5e为裂缝面形状（矩形和正方形）对钻井液漏失速率的影响，可以看出：无论是漏失初始阶段还是漏失末段，正方形裂缝的漏失速率均高于矩形裂缝。

3.4 裂缝面滤失性的影响

（5）式采用Carter滤失模型[6,15]求取钻井液通过裂缝面的滤失量，式中的综合滤失系数由钻井液黏度滤失系数、地层流体滤失系数和钻井液泥饼滤失系数计算得到。分析了不同井底压差下裂缝面滤失性对钻井液漏失速率的影响（见图6）。

由图6可知：在相同井底压差条件下，裂缝面的综合滤失系数越高，钻井液漏失速率越高；在漏失初始阶段，漏失速率快速下降，随着漏失的进行，钻井液在裂缝面上逐渐形成泥饼，造成钻井液漏失速率逐渐降低直至达到平衡状态；随着井底压差的增大，裂缝面滤失性对钻井液漏失速率的影响也越来越明显，因此通过调整井底压差可降低钻井液在裂缝面的滤失量。

3.5 其他参数

井眼与裂缝相交位置、井底压差和裂缝法向刚度也会对钻井液漏失速率产生影响。

图7为井眼与裂缝相交位置（裂缝中心、裂缝边界中点和裂缝角点）对钻井液漏失速率的影响，可以看出：3种位置的漏失速率峰值相差不大，但是后续漏失中井眼与裂缝相交在裂缝中心时的钻井液漏失速率最大，其次是裂缝边界中点，裂缝角点时最小。这是由于3种井眼与裂缝相交位置的边界条件不同，钻井液在缝内流动受到的限制不同。

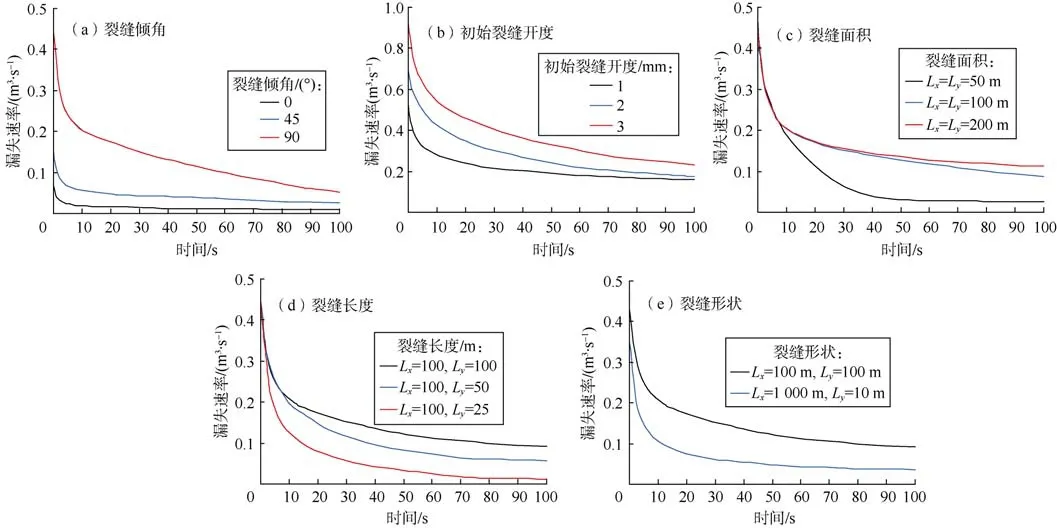
图5 裂缝几何参数对钻井液漏失速率的影响

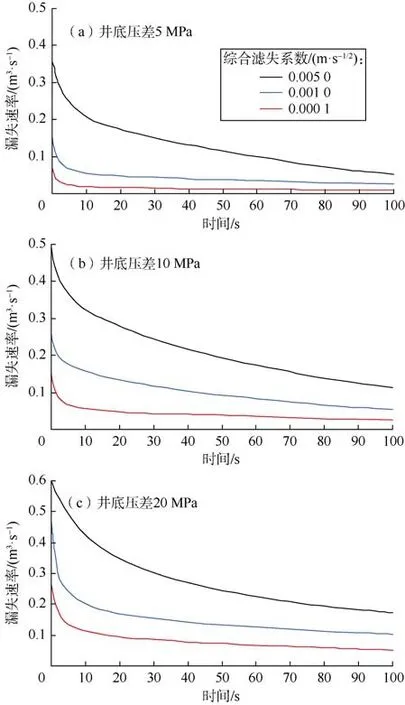
图6 裂缝面滤失性对漏失速率的影响

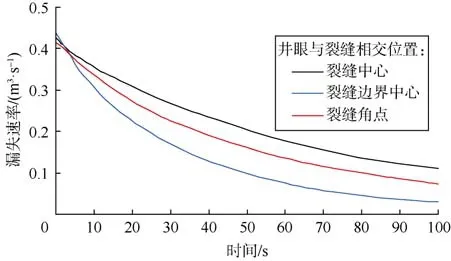
图7 井眼与裂缝相交位置对钻井液漏失速率的影响

保持缝内初始压力20 MPa不变，分别取井内压力为25 MPa、30 MPa和40 MPa，可得到3种不同的井底压差（5 MPa、10 MPa和20 MPa）。图8为不同井底压差下钻井液漏失速率的变化曲线，可以看出：当井底压差增大时，钻井液漏失速率明显变大。这是由于井底压差是钻井液漏失的主要驱动力，井底压差越高，钻井液漏失问题越严重。

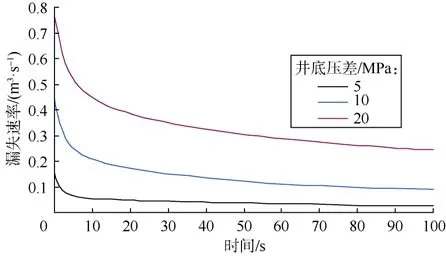
图8 井底压差对钻井液漏失速率的影响

图9 为裂缝法向刚度对钻井液漏失速率的影响，可以看出：随着裂缝法向刚度增大，钻井液漏失速率会降低。由（3）式可知，裂缝法向刚度越高，在缝内压力作用下裂缝开度越不容易发生变化。因此，在相同的缝内压力和初始裂缝开度条件下，裂缝法向刚度较高时，裂缝开度会保持稳定或变化极小，钻井液漏失速率也会相应降低。

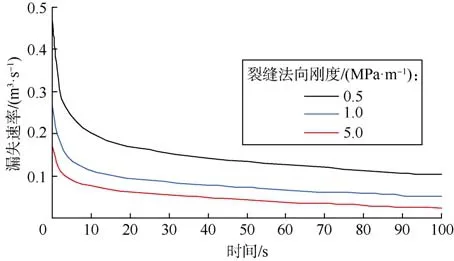
图9 裂缝法向刚度对漏失速率的影响

4 结论

本文建立了二维单条裂缝的幂律模式钻井液漏失模型，该模型中将裂缝看作任意倾角的粗糙裂缝且裂缝面具有渗透性，并假设裂缝开度满足线性变形规律。利用质量守恒定律和Reynolds方程得到了钻井液漏失控制方程，该方程中体现了裂缝面粗糙度、裂缝变形和裂缝面滤失性的影响。

利用所建立的钻井液漏失模型，研究了不同参数对钻井液漏失速率的影响。结果表明：①幂律模式钻井液的剪切稀释性会造成漏失初始阶段漏失速率的升高。②裂缝迂曲度对钻井液漏失速率有很大影响，钻井液漏失速率随裂缝迂曲度的变大而减小，但是随着裂缝开度的增加裂缝迂曲度对钻井液漏失速率的影响降低。③初始裂缝开度、裂缝倾角、裂缝面积、裂缝长度越大，钻井液漏失速率越大；矩形裂缝的钻井液漏失速率低于正方形裂缝。④对于渗透性地层，裂缝面滤失性引起的钻井液漏失不可忽视。裂缝面滤失综合系数越大，钻井液漏失速率越高。⑤井眼与裂缝相交于裂缝中心位置时钻井液漏失速率最高，其次为裂缝边界中心，裂缝角点时最低；随着井底压差的增加，钻井液漏失速率会明显升高；裂缝法向刚度越高，钻井液漏失速率越小。

符号注释：

D——裂缝分形维数；H——裂缝Hurst指数；wm——裂缝力学开度，m；wh——裂缝水力开度，m；δ——裂缝迂曲度；α——裂缝倾角，（°）；Lx，Ly——沿x轴和y轴方向的裂缝长度，m；pi——裂缝内初始压力，Pa；t——模拟时间，s；pw——井内压力，Pa；τ——剪切应力，Pa；K——稠度系数，Pa·sn；n——流动特性指数；γ——剪切速率，s-1；p——裂缝内某一点压力，Pa；Kn——裂缝法向刚度，Pa/m；wh0——初始压力pi时的初始裂缝开度，m；，——钻井液沿x轴和y轴方向的流速，m/s；q——裂缝面钻井液滤失速度，m/s；Ct——裂缝面钻井液综合滤失系数，m/s1/2；τD——裂缝内某点开始滤失的时间，s；ρ——钻井液密度，kg/m3；g——重力加速度，m/s2。

[1] Dyke C G, Wu B, Milton-Tayler D. Advances in characterizing natural fracture permeability from mud-log data[J]. SPE Formation Evaluation, 1995, 10(3): 160-166.

[2] Bertuzzi F, Sanfilippo F, Brignoli M, et al. Characterization of flow within natural fractures: Numerical simulations and field applications[R]. SPE 47268, 1997.

[3] Beda G, Carugo C. Use of mud microloss analysis while drilling toimprove the formation evaluation in fractured reservoirs[R]. SPE 71737, 2001.

[4] Lietard O, Guillot D, Hodder M. Fracture width LWD and drilling mud/LCM selection guidelines in naturally fractured reservoirs[R]. SPE 36832, 1996.

[5] Sanfillippo F, Brignoli M, Santarelli F J, et al. Characterization of conductive fractures while drilling[R]. SPE 38177, 1997.

[6] Lavtov A, Tronvoll J. Mud loss into a single fracture during drilling of petroleum wells: Modeling approach[C]//Proceedings of 6th International Conference on Analysis of Discontinuous Deformation. Trondheim, Norway: International Society for Rock Mechanics, 2003: 189-198.

[7] Lavtov A, Tronvoll J. Modeling mud loss in fractured formations[R]. SPE 88700, 2004.

[8] Lavtov A. Newtonian fluid flow from an arbitrarily-oriented fracture into a single sink[J]. Acta Mechanica, 2006, 186(1/2/3/4): 55-74.

[9] Majidi R, Miska S Z, Yu M, et al. Quantitative analysis of mud losses in naturally fractured reservoirs: The effect of rheology[J]. SPE Drilling & Completion, 2010, 25(4): 509-517.

[10] Majidi R, Miska S Z, Yu M, et al. Modeling of drilling fluid losses in naturally fractured formations[R]. SPE 114630, 2008.

[11] Majidi R, Miska S Z, Yu M, et al. Fracture ballooning in naturally fractured formations: Mechanism and controlling factors[R]. SPE 115526, 2008.

[12] Ozdemirtas M, Babadagli T, Kuru E. Effects of fractal fracture surface roughness on borehole ballooning[J]. Vadose Zone Journal, 2009, 8(1): 250-257.

[13] Ozdemirtas M, Kuru E, Babadagli T. Experimental investigation of borehole ballooning due to flow of non-Newtonian fluids into fractured rocks[J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(7): 1200-1206.

[14] Shahri M P, Mehrabi M. A new approach in modeling of fracture ballooning in naturally fractured reservoirs[R]. SPE 163382, 2012.

[15] 李大奇. 裂缝性地层钻井液漏失动力学研究[D]. 成都: 西南石油大学, 2012.

Li Daqi. Numerical and experimental investigations of drilling fluid losses in fractured formations[D]. Chengdu: Southwest Petroleum University, 2012.

[16] Tsang Y W. The effect of tortuosity on fluid flow through a single fracture[J]. Water Resources Research, 1984, 20(9): 1209-1215.

[17] Brown S R, Scholz S H. Broad bandwidth study of the topography of natural rock surfaces[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 1985, 90(B14): 12575-12582.

[18] Brown S R. Fluid flow through rock joints: The effect of surface roughness[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 1987, 92(B2): 1337-1347.

[19] Brown S R, Stockman H W, Reeves S J. Applicability of the Reynolds equation for modeling fluid flow between rough surfaces[J]. Geophysical Research Letters, 1995, 22(18): 2537-2540.

[20] Renshaw C E. On the relationship between mechanical and hydraulic apertures in rough-walled fractures[J]. Journal of Geophysical Research, 1995, 100(B12): 24629-24636.

[21] Ge S M. A governing equation for fluid flow in rough fractures[J]. Water Resources Research, 1997, 33(1): 53-61.

[22] Glover P W J, Matsuki K, Hikima R, et al. Fluid flow in fractally rough synthetic fractures[J]. Geophysical Research Letters, 1997, 24(14): 1803-1806.

[23] Di Federico V. Non-Newtonian flow in a variable aperture fracture[J]. Transport in Porous Media, 1998, 30(1): 75-86.

[24] Di Federico V. On non-Newtonian fluid flow in rough fractures[J]. Water Resources Research, 2001, 37(9): 2425-2430.

[25] Zimmerman R W, Kumar S, Bodvarsson G S. Lubrication theory analysis of the permeability of rough-walled fractures[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1991, 28(4): 325-331.

[26] Zimmerman R W, Chen D, Cook N G W. The effect of contact area on the permeability of fractures[J]. Journal of Hydrology, 1992, 139(1): 79-96.

[27] Yeo I W, Ge S M. Applicable range of the Reynolds equation for fluid flow in a rock fracture[J]. Geosciences Journal, 2005, 9(4): 347-352.

[28] Wait M, Ge S, Spetzler H. A new conceptual model for fluid flow in discrete fractures: An experimental and numerical study[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 1999, 104(B6): 13049-13059.

[29] Murata S, Saito T. Estimation of tortuosity of fluid flow through a single fracture[J]. Journal of Canadian Petroleum Technology, 2003, 42(12): 39-45.

Drilling fluid loss model and loss dynamic behavior in fractured formations

Jia Lichun1, Chen Mian1, Hou Bing1, Sun Zhen2, Jin Yan1
(1. State Key Laboratory of Petroleum Resource and Prospecting, China University of Petroleum, Beijing 102249, China; 2. Petroleum Engineering Technology Research Institute, Sinopec Jiangsu Oilfield, Yangzhou 225009, China)

In view of the lost circulation in fractured formations, a two-dimensional transient model for describing a power-law drilling fluid loss in an arbitrarily-oriented, compressible, permeable, rough-walled fracture was introduced. In this model, the mechanical fracture aperture and fracture tortuosity were considered to investigate the effect of fracture roughness on fluid loss dynamics. The governing equation of power-law fluid loss model was given and solved to analyze the fluid loss dynamics in fractured formations. The results show that the shear thinning behavior of power-law drilling fluid can result in high fluid loss rate at the initial stage of loss event; the fluid loss rate decreases as the fracture tortuosity increases, meanwhile, the effect of fracture tortuosity on fluid loss rate will decrease as the fracture aperture becomes larger; the larger the initial fracture aperture, fracture dip, fracture dimensions or fracture length, the higher the fluid loss rate will be; the fluid loss rate of rectangular fractures is much lower than that of square fractures; the higher the total leak-off coefficient, the higher the fluid loss rate will be; the fluid loss rate is the highest when the wellbore intersects the fracture at the center location; the fluid loss rate increases sharply as the differential pressure increases; the larger the normal stiffness of the fracture, the lower the mud loss rate will be.

fractured formation; lost circulation; fracture; power-law fluid; fluid loss model; fluid loss rate

TE254

A

贾利春（1985-），男，河北邯郸人，现为中国石油大学（北京）石油工程学院博士研究生，主要从事油气井岩石力学与工程方面的研究工作。地址：北京市昌平区府学路18号，中国石油大学（北京）289信箱，邮政编码：102249。E-mail: jialc802@gmail.com

联系作者：金衍（1972-），男，浙江临海人，中国石油大学（北京）石油工程学院教授、博士生导师。地址：北京市昌平区府学路18号，中国石油大学（北京）289信箱，邮政编码：102249。E-mail: jinyan_cup@163.com

2013-06-29

2013-10-26

（编辑 胡苇玮 绘图 刘方方）

1000-0747(2014)01-0095-07

10.11698/PED.2014.01.12

国家自然科学基金项目“深部应力敏感裂缝性地层漏失封堵力学机理研究”（51204195）