基于TW-TOA的面向合作传感器网络多节点定位方案

汤 岩， 聂 萌

(1.东北农业大学 理学院，黑龙江 哈尔滨 150030；2.积成电子股份有限公司 ，山东 济南 250100)

基于TW-TOA的面向合作传感器网络多节点定位方案

汤 岩1， 聂 萌2

(1.东北农业大学 理学院，黑龙江 哈尔滨 150030；2.积成电子股份有限公司 ，山东 济南 250100)

针对合作传感器网络的定位问题，提出在未知节点周转时间 (TATs)条件下估计多个目标节点位置的方案。在该方案中，每个目标节点能与多个锚节点、其他目标节点通信，并测量它们间的双向到达时间 (TW-TOA)值，其包括在信道终端的处理时延。基于这些测量值，对目标节点位置和TATs进行最大似然估计 (MLE)，而这产生了非凸优问题，为此，将其近似转化为非线性最小二乘问题。最后，通过欧氏距离矩阵 (EDM)对多个目标节点位置和TATs的值进行估计。仿真结果表明：提出的方案具有良好的定位精度。在不同的场景下，提出的方案的均方根误差逼近克莱姆—拉奥下限 (CRLB)。

合作传感器网络； 定位； 周转时间； 双向到达时间； 欧氏距离矩阵； 克莱姆—拉奥下限

0 引 言

无线传感器网络 (wireless sensor networks,WSNs)应用时均需要对传感器节点进行精确的定位[1]。在噪声测量环境中，常采用双向到达时间 (two-way time of arrival,TW-TOA)方案进行估计节点的位置。TW-TOA要求锚节点Anchor(已知位置坐标的节点)向目标节点发送测距请求，并且目标节点收到之后进行回复。目标节点在收到请求时会产生反应时间，称为周转时间 (turn-around times，TATs)，并将其存入回复的数据包中。若不考虑目标节点的TATs，请求信号的发送和接收所经历的时间正比于目标节点与锚节点间的距离[2]。然而，在实际环境中，节点的TATs是不容忽略的，并且部分目标节点可能通过报告错误的TATs欺骗锚节点。为此，定位算法就应考虑节点的TATs。

在非合作式的传感器网络，目标节点只能与锚节点进行通信[3]。这限制了目标节点与目标节点的通信连接，为此，提出合作式定位方案。在合作式定位方案中，目标节点不仅与目标节点，还与锚节点通信。因此，不仅目标节点与锚节点间的到达时间(times-of-arrival,TOA)需要测量，而且目标节点与目标节点间的TOA也需要测量。

通过TOA测量值，建立定位方程组。在异步网络中，常采用封闭式的最小二乘 (least squares,LS)估计算法对单个的目标节点进行定位。文献[4]提出非对称测距(asymmetric trip ranging,ATR)方案。在ATR中，锚节点不仅能与目标节点通信，而且能够监听其他锚节点与目标节点的通信。文献[5]提出了异步位置测量方案,该方案通过到达时间差(time difference of arrival，TDOA)，并采用LS算法对室内单个的目标节点进行位置估计。文献[6]采用联合同步，提出广义的LS算法估计目标节点的位置。文献[7]针对合作网络中，提出基于LS的TW-TOA和TDOA的混合算法，对节点位置和TATs的估计。然而，这些方案没有考虑到目标节点间的TW-TOA的测量值，这些测量值可提供定位精度。

为此，针对合作网络并未知TATs的环境下， 对多个目标节点进行定位方案进行研究。在未知TATs的情况下，需采用最大似然估计(maximum likelihood estimator,MLE)算法。通过MLE解决非线性、非凸优问题。然而，通过MLE解决非凸优问题，计算复杂，并且计算量大。因此，需将MLE问题转为近似非线性最小二乘 (nonlinear least squares,NLS)问题。然后，再通过欧氏距离矩阵 (Euclidean distance matrix,EDM)将NLS问题转为凸优问题。通过这种方式，将非凸优问题转为凸优问题，从而使得目标节点的TATs成为冗余参数，也就是未知TATs，不影响多个目标节点的位置估计。

1 问题描述

本节阐述通过TW-TOA测量，并未知目标节点位置和TATs的合作定位问题。

估计者需要2个TW-TOA的测量集数据：目标节点与锚节点 (target-to-anchor,T2A)、目标节点与目标节点 (target-to-target,T2T)。假定N个目标节点、M个锚节点。N个目标节点的位置sj∈Rl，且j∈S={1,2,…,N}。M个锚节点的位置αi∈Rl，且i∈A={N+1,N+2,…,N+M}。此外，定义2个节点集Bj,Cj，定义如式(1)、式(2)所示

Bj={i|anchoricancommunicatewithtargetj},

(1)

Cj={i|targeticancommunicatewithtargetj}.

(2)

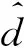
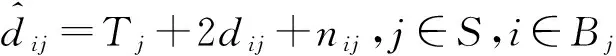
(3)

其中,Tj表示目标节点j的迂回时间TATs。如果i∈Cj，则dij=‖si-sj‖；若i∈B，则dij=‖ai-sj‖。此外，nij表示独立同分布的零均值高斯随机变量，且标准偏差σij[1]。

依据式(3)，存在l×N+N个未知元素待估计，包括目标节点位置和迂回时间TATs分别为S=[s1,……,sN]∈Rl×N,T=[T1,…,TN]T∈RN。

在实际的场景中，假定目标节点i向另一个目标节点j发送测距请求，节点j收到并回复。如果节点i收到该回复就发送最终的数据包。在这个过程中，获取到了2个TW-TOA的测量值。若是锚节点向目标节点发送测距请求，目标节点不仅回复测距消息，同时也要发送与其他目标节点的TW-TOA测量值。

1.1EDM描述

注意式(3)，将右边的Tj移至等式左边，并等式两边同时平方，可得式(4)

(4)

(5)

其中，ζij=4dijnij表示零均值的高斯噪声，标准偏差为4dijσij。

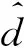
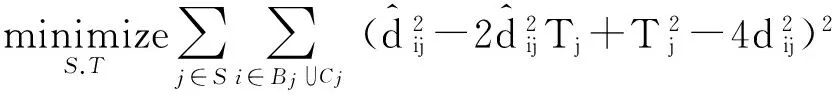
(6)

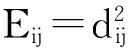
如果矩阵E满足式(7)，矩阵E属于EDM矩阵[8,9]

Eii=0,Eij≥0,-JEJ>0.

(7)

引入变量K=[K1,…,KN]T，并构建目标函数，如式(8)所示

subject toE∈ζ,E(A)=A,

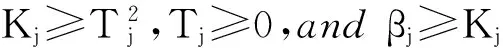
(8)

为了解决这个问题，向目标函数添加正则项[10]改变大的Kj值，然而，该方式带来大的计算量。另一种解决办法：通过常量βj限定Kj的上限。βj的设定见1.2节。

1.2 βj的估计

针对Kj，需合理估计βj的值。若i∈Bj，dij=‖ai-sj‖，移除式(5)中的噪声项ζij，可得式(9)

(9)

对式(9)进行整理[11～13]

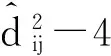
(10)

此外，设定向量bj、矩阵Hj，致使bj=Hjyj。如果Hj为列满秩，通过LS算法对sj,Tj进行估计，如式(11)所示

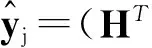
(11)

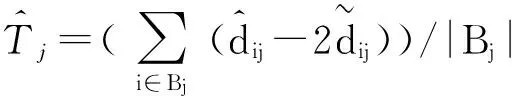
(12)

2 仿 真

本节通过VC++软件对提出的算法进行仿真，将提出的算法记为EDM，并分析EDM性能。将均方根误差 (root mean-square error,RMSE)作为性能指标，如式(13)

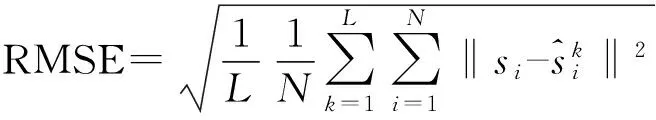
(13)

此外，为了分析位置估计的难度，针对每个噪声方差，描绘了在已知TATs、未知TATs环境下的误差曲线的克莱姆—拉奥下限 (Cramer-Rao lower bound,CRLB)[2]，并分别记为CRLB-Known-T,CRLB。

同时，为了提出的算法与MLE进行比较，引用Matlab软件的库里的函数lsqnonlin。将提出算法输出作为该函数初始值，此算法记为EDM-MLE。若随机初始化，记为RAND-MLE。此外，进一步地分析TATs对提出算法EDM，将已知TATs的EDM算法，记为EDM-Known-T。

在仿真过程中，TATs从[1，100]ns中随机取值，噪声服从独立同分布的高斯白噪声，且方差σij=σ∈[0.01,18]m。

1)实验1：本次实验考虑全连通的分布网络，即所有的锚节点、目标节点均在通信范围内。仿真区域为[-80,80]m×[-80,80]m，8个锚节点、6个目标节点，仿真结果如图1所示。

图1 分布式全连通的网络下RMSE随误差的变化曲线Fig 1 RMSE vs error in a fully connected distributed network

从图1可知，提出的算法EDM具有较高的定位精度，远高于RAND-MLE，略低于CRLB-Known-T。这主要是因为EDM未知TATs，导致其定位精度的下降。但是其与已知EDM-Known-T方案仅低了约1m。

2)实验2：本次实验考虑结构化网络，由6个目标节点和8个锚节点构成，并且网络是全连通状态。

8个锚节点和6个目标节点的坐标分别为

ai∈{[±50,±50]T,[00,±70]T,[±70,0]T}m,

si∈{[±20,40]T,[0,±40]T,[0,0]T,[20,-40]T}m.

仿真结果如图2所示。

图2 结构化全连通的网络下RMSE随误差的变化曲线Fig 2 RMSE vs error in a fully connected structured network

如图2所示，在结构化全连通网络下，提出的算法EDM也表现出良好的定位精度。从图2可知，EDM-MLE逼近CRLB。与图1(实验1)不同是，RAND-MLE的RRSE近似于CRLB。这主要是因为RAND-MLE的目标函数具有唯一最小值。

3)实验3:本次实验针对结构化非连通网络进行仿真，并且σ=10m。图3中三角形表示显示锚节点，方块表示目标节点，圆形表示提出的算法EDM对目标节点的位置估计。从图3可知，在σ=10的情况下，提出的算法还是较准确在估计目标节点的位置。

图3 EDM对8个目标节点的定位(σ=10 m)Fig 3 Localization of eight target nodes by EDM (σ=10 m)

图4显示了RAND-MLE,EDM,EDM-MLE,EDM-Known-T,CRLB和CRLB-Known-T在结构化非全连通的网络环境下的RMSE性能曲线。从图4可知，RAND-MLE的RMSE随σ变化波动性大。而EDM表示较高的稳定性。同图2相比，非全连通的网络致使RMSE性能下降。

图4 结构化非全连通的网络下RMSE随误差的变化曲线Fig 4 RMSE vs error in a nun-fully connected distributed network

3 结 论

针对无线传感网络的定位问题展开分析，并提出基于TW-TOA的EDM的多节点定位算法。该算法利用锚节点与目标节点间TW-TOA值，对目标节点位置和TATs进行MLE，并将MLE产生非凸优问题转为为凸优问题，最后，利用通EDM算法估计多个目标节点位置和TATs的值。仿真结果表明：提出的定位算法能准确地估计节点位置。

[1]SahinogluZ,GezicSI,GuvencI.Ultra-widebandpositioningsytems:Theoreticallimits,rangingalgorithmsandprotocols[M].Cambridge:CambridgeUniversityPress,2008.

[2]PatwariN,HeroA,PerkinsM,etal.Relativelocationestimationinwirelesssensornetworks[J].IEEETransactionsonSignalProcessing,2013,51(8):2137-2148.

[3]CheungKW,SoHC,MaWK,etal.Aconstrainedleastsquaresapproachtomobilepositioning:Algorithmsandoptimality[C]∥EURASIPJournalonAppliedSignalProcessing,2006:1-6.

[4]WangY,MaX,LeusG.Robusttimebasedlocalizationforasynchronousnetworks[J].IEEETransactionsonSignalProcessing,2011,59(9):4397-4410.

[5]ZhouY,LawCL,GuanYL,etal.IndoorellipticallocalizationbasedonasynchronousUWBrangemeasurement[J].IEEETransactionsonSignalProcessing,2011,60(1):248-257.

[6]ZhengJ,WuYC.Jointtimesynchronizationandlocalizationofanunkownnodeinwirelesssensornetworks[J].IEEETransactionsonSignalProcessing,2010,58(3):1309-1320.

[7]GholamiMR,GeziciS,StromEG.ImprovedpositionestimationusinghybridTW-TOAandTDOAincooperativenetworks[J].IEEETransactionsonSignalProcessing,2010,60(7):3770-3785.

[8]BoydS,VandenbergheL.Convexoptimization[M].Cambridge:CambridgeUniversityPress,2004.

[9]EkimPO,GomesJ,XavierJ,etal.Robustlocalizationofnodesandtime-recursivetrackinginsensornetworksusingnoisyrangemeasurements[J].IEEETransactionsonSignalProcessing,2011,59(8):3930-3942.

[10]DattorroJ.ConvexoptimizationandEuclideandistancegeome-try[M].PaloAlto:MebooPublishers,2005.

[11]BiswasP,LiangT,TohK,etal.Semi-definiteprogrammingapproachesforsensornetworklocalizationwithnoisydistancemeasurements[J].IEEETransactionsonAutomationScienceandEngineering,2006,3(4):360-371.

[12]Oguz-EkimP,GomesJ,XavierJ,etal.ML-basedsensornetworklocalizationandtracking:Batchandtime-recursiveapproache-s[C]∥EU-SIPCO’09,Glasgow,Scotland,2009:45-52.

[13]BiswasP,LiangT,WangT,etal.Semi-definiteprogrammingbasedalgorithmsforsensornetworklocalization[J].ACMTransactionsonSensorNetworks(TOSN),2006,2(2):188-220.

[14]ZhouY,LawCL,GuanYL.LocalizationofpassivetargetbasedonUWBbackscatteringrangemeasurement[C]∥ProcofIEEEICUWB,2009:145-149.

[15]SharpI,YuK,GuoYJ.GDOPanalysisforpositioningsystemdesign[J].IEEETransonVehTechnol,2009,58(7):3371-3382.

Scheme of TW-TOA-based multiple node localization in cooperative sensor network

TANG Yan1, NIE Meng2

(1.College of Science,Northeast Agricultural University,Harbin 150030,China;2.Integrated Electronic Systems Lab Co Ltd,Jinan 250100,China)

Aiming at localization problem of cooperative sensor network,propose scheme to estimate multiple nodes positions in the presence of unknown turn-around times(TATs).In the adopted scheme,each target node can communicate with several anchor nodes and other target nodes,and two-way times-of-arrival between them are measured,which includes processing delays at both channel endpoints.The maximum likelihood estimates (MLE) of positions of target node and turn-around times(TATs) is carried out based on those measurement value,which generate non-convex optimization problem,it is approximated transform to nonlinear least squares problem.Finally,positions and TATs of multiple target nodes are estimated jointly by solving Euclidean distance matrix.Simulation result show that the proposed method has good localization precision,under different scenes,RMSE of the proposed scheme approach the Cramer-Rao lower bound (CRLB).

cooperative sensor network; localization; turn-around times(TATs); two-way times-of-arrival(TW-ToA); Euclidean distance matrix(EDM); Cramer-Rao lower bound(CRLB)

10.13873/J.1000—9787(2014)08—0127—04

2014—05—15

TP 393

A

1000—9787(2014)08—0127—04

汤 岩(1979-),女,黑龙江哈尔滨人,硕士,讲师,主要研究领域为概率统计、车载网。