用于速度分布测量的多电极静电传感器优化设计*

王 超， 吴伟平， 张文彪

(天津大学 电气与自动化工程学院 天津市过程检测与控制重点实验室，天津 300072)

用于速度分布测量的多电极静电传感器优化设计*

王 超， 吴伟平， 张文彪

(天津大学 电气与自动化工程学院 天津市过程检测与控制重点实验室，天津 300072)

通过介绍静电相关速度分布测量原理，说明实现不同侧电极静电信号有效相关计算的重要性。为保证不同侧相关有效性，对多电极静电传感器进行有效相关分析，提出有效相关分析方法，进行多电极静电传感器结构优化。最后经过实验验证，优化后的多电极静电传感器不同侧电极静电信号能够实现有效的相关计算，为进一步研究速度分布的测量奠定了基础。

速度分布； 传感器优化； 多电极静电传感器； 有效相关计算

0 引 言

气力输送系统广泛应用于工业生产过程，如，电厂煤粉输送、水泥厂水泥输送和炼钢厂高炉喷粉系统等，固体粉料的移动速度是描述这些过程的一个重要参数。由于气固两相流的流场复杂，且具有不同的速度分布，使得不同速度测量方法的理论结果与实际物理意义缺乏依据，所以，实现稀相气固两相流速度分布测量尤为重要。对于浓相气固相两相流速度分布的在线测量，电容层析成像(ECT)与互相关技术相结合是常用的方法[1]；另外，奥地利Anton Fuchs等人提出了多电极的电容传感器，将采集自上游7个电极与下游7个电极信号两两相关获得49个相关速度，进而实现速度分布的在线测量[2]；然而，对于稀相气固两相流，由于固体颗粒的体积分数有限，电容测量的灵敏度难以达到要求，因此，本文设计了多电极静电传感器，利用静电传感原理与互相关测量技术相结合实现速度分布的在线测量，为了实现不同侧电极对静电信号的有效相关计算，对传感器结构进行了优化。

1 静电相关速度分布测量原理

用于速度分布测量的多电极静电传感器示意图如图1所示，绝缘层内径为50 mm。该静电传感器阵包括2组弧形电极，分处上游和下游截面，记为第1，2组，上游和下游截面距离48 mm，每组电极包括4个，安装于各自截面圆周上，根据位置不同，分别以A～D的字母标记。在进行互相关计算时，上下游相同位置电极信号相关称为同侧相关；相邻位置为邻侧相关；间隔一个位置的相关为对侧相关。

利用上述多电极静电传感器，将采集自上游4个电极与下游4个电极信号两两相关可获得16个相关速度。由于不同区域的带电颗粒对静电检测信号的贡献是不同的，因此,不同对电极测量的相关速度对不同区域颗粒的速度的表征权重存在差别，如图2所示。从图2中可以看出:A-A同侧相关计算得到的相关速度主要反映的是靠近管道边缘的固体颗粒速度；A-B邻侧相关计算得到的相关速度主要反映两弧形电极之间靠近管道边缘颗粒的速度；A-C对侧相关计算得到的相关速度主要反映的是管道中心区域的固体颗粒速度。根据该特点，可以16个相关速度为基础，初步估计固体颗粒的速度分布情况。

图1 多电极静电传感器示意图Fig 1 Diagram of multi-electrode electrostatic sensor

图2 上下游不同位置电极信号相关速度对不同位置速度表征的权重分布Fig 2 Weight of particle velocity distribution represented by the correlation velocity which is calculated by the electrostatic signals of different electrode couples

2 多电极静电传感器有效相关分析

定义静电传感器灵敏度为

S(x,y,z)=|Q/q(x,y,z)|.

(1)

其中,S(x,y,z)为管道截面的横坐标x和纵坐标y及管道的轴向坐标z处的灵敏度；Q为电极上的感应电荷量；q(x,y,z)为颗粒电荷量[3]。

利用COMSOL软件计算单个弧形电极的灵敏度分布如图3所示，可以发现电极附近的区域的灵敏度远远高于其它区域，当进行邻侧和对侧相关时，2个电极获取的信号中，表征临近电极区域颗粒动态信息的信号很强，但是在邻侧和对侧相关计算时这些信号并不相关，从而导致除了同侧相关，尤其是对侧相关很难获得有效的相关结果。

图3 单个弧形电极的灵敏度分布Fig 3 Sensitivity distribution of single arc-electrode

为了使不同侧相关，尤其对侧相关，取得较好的相关结果，本文提出一种有效相关分析方法，以此深入研究对侧相关;并且以对侧相关的渡越时间准确率 表示对侧相关计算的有效性。

随机产生3个随机数组成的时间序列，分别为m(t),n(t)和p(t)，表示管道截面中m,n和p 3个位置的电荷波动，其中，m的坐标为(0,24)mm，n的坐标为(0,0)mm，p的坐标为(0,-24)mm。Sm,A,Sn,A,Sp,A和Sm,C,Sn,C,Sp,C为电极A和C对上述3个位置的灵敏度。假设下游流动信号滞后于上游流动信号100个时间步长，上游A电极和下游C电极检测的静电信号时间序列为

eA(t)=Sm,A×m(t)+Sn,A×n(t)+Sp,A×p(t),

(2)

eC(t)=Sm,C×m(t+100)+Sn,C×n(t+100)+ Sp,C×p(t+100).

(3)

对这2个信号进行相关计算，求取渡越时间，进行相关计算的有效性分析。

3 多电极静电传感器结构优化

静电传感器优化的关键在于，通过优化设计，使整个管道截面空间灵敏度分布更加均匀，并保证对侧相关计算的有效性。

3.1 电极轴向宽度分析

利用COMSOL软件，对绝缘层厚度为0 mm，电极轴向宽度分别为2,6,10,14,18 mm时的灵敏度分布进行仿真，求得上游A电极和下游C电极在m,n,p位置的灵敏度。采用有效相关计算分析方法， 100次实验渡越时间准确率均为0，相关计算很难达到要求。

3.2 绝缘层厚度分析

管道内径固定，绝缘层材料选择为有机玻璃，增加绝缘层厚度，利用COMSOL软件对不同绝缘层厚度的多电极静电传感器进行仿真，分别求得绝缘层厚度为5,6,7,8 mm上游A电极和下游C电极在m,n,p位置的灵敏度。采用有效相关计算分析方法，100次实验渡越时间准确率如图4所示。可知，随着绝缘层厚度的增加，利用互相关法求得的渡越时间准确率逐渐提高。当绝缘层厚度增加至8 mm，利用互相关法可以非常准确地求得对侧相关的渡越时间，因此，多电极静电传感器的绝缘层厚度选为8 mm。

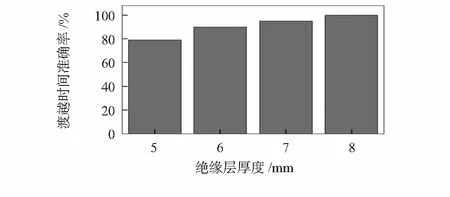
图4 A-C对侧相关渡越时间的准确率Fig 4 Accuracy of transit time of A-C opposite side correlation

4 实验结果

分别制作绝缘层厚度为0,8 mm的多电极静电传感器，如图5所示。

图5 多电极静电传感器的实物图Fig 5 Physical picture of multi-electrode electrostatic sensor

首先，利用天津大学的带式静电感应实验装置进行实验[4]。实验过程中，3条橡胶带位于管道的中心平面上，两侧橡胶带距中心橡胶带的距离相等分别为19 mm，并且3条橡胶带的速度均一致。

根据实验采集的上下游不同电极对静电信号进行相关计算，实验结果如图6和图7所示。实验结果表明:绝缘层厚度为0 mm的多电极静电传感器邻侧和对侧相关得到的相关速度与橡胶带的速度差距较大，而绝缘层厚度为8 mm的多电极静电传感器邻侧和对侧相关得到的相关速度与橡胶带的速度一致，这说明绝缘层厚度为8 mm的多电极静电传感器能够实现不同电极对有效地相关计算。

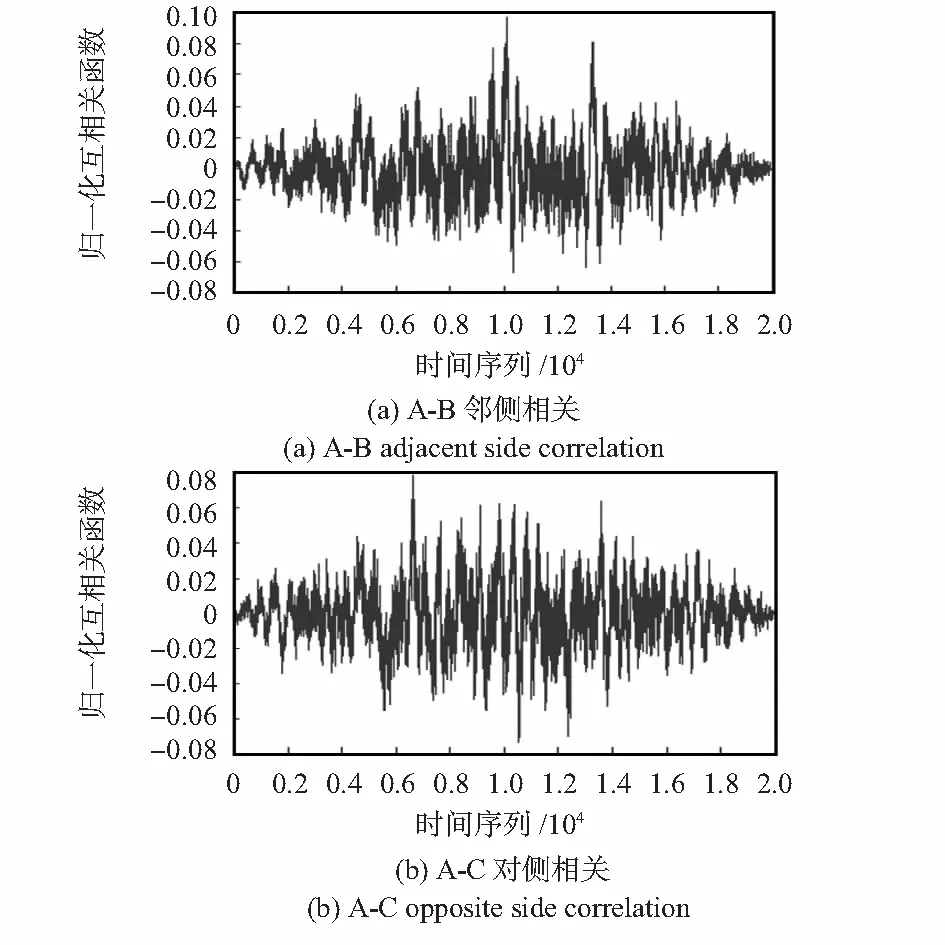
图6 不同电极对静电信号的相关函数 (绝缘层厚度为0 mm)Fig 6 Correlation function calculated by electrostatic signal of different electrode couples(thickness of insulation layer is 0 mm)

图7 不同电极对静电信号的相关函数 (绝缘层厚度为8 mm)Fig 7 Correlation function calculated by electrostatic signal of different electrode couples(thickness of insulation layer is 8 mm)

利用绝缘层厚度为8 mm的多电极静电传感器，结合天津大学气固两相流实验装置进行了实验[4]。根据实验采集的上下游不同电极对静电信号进行相关计算，实验结果如图8所示。从图8中可以看出：同侧电极静电信号的相关性最好，邻侧电极次之，对侧电极静电信号的相关性最差，但其相关函数的峰值仍十分明显，由此可以说明该传感器结构优化的有效性。

5 结 论

本文首先通过介绍静电相关速度分布测量原理，说明实现不同侧电极静电信号有效相关计算的重要性。接着对多电极静电传感器进行有效相关分析，提出有效相关分析方法，进行多电极静电传感器结构优化，并在带式静电感应装置上验证优化后的多电极静电传感器能够实现有效地不

图8 不同电极对静电信号的相关函数Fig 8 Correlation function calculated by electrostatic signals of different electrode couples

同侧相关计算。最后经过气固两相流装置实验验证，优化后的多电极静电传感器不同侧电极静电信号能够实现有效的相关计算，这为实现兼顾管道横截面中心区域和边缘区域的速度分布测量奠定了基础。

[1] Datta U,Dyakowski T,Mylvaganam S.Estimation of particulate velocity components in pneumatic transport using pixel based correlation with dual plane ECT[J].Chemical Engineering Journal,2007,130(2):87-99.

[2] Fuchs A,Zangl H,Wypych P.Signal modelling and algorithms for parameter estimation in pneumatic conveying[J].Powder Technology,2007,173(2):126-139.

[3] 王玉琳.用于稀相气固两相流测量的多电极静电传感器研究[D].天津：天津大学，2011.

[4] 王 超，王玉琳，张文彪.基于静电感应的气固两相流测量及研究装置[J].电子测量与仪器学报，2011，25(1)：1-9.

Optimization design of multi-electrode electrostatic sensor for velocity distribution measurement*

WANG Chao， WU Wei-ping， ZHANG Wen-biao

(Tianjin Key Laboratory of Process Measurement and Control,School of Electrical Engineering and Automation,Tianjin University,Tianjin 300072,China)

By introducing principle of electrostatic correlation based velocity distribution measurement，importance of effective correlation calculation by non-corresponding side electrode couples is emphasized.In order to ensure its effectiveness,effective correlation analysis on multi-electrode electrostatic sensor is carried out,and effective correlation analysis method is proposed,according to this,the structure of multi-electrode electrostatic sensor is optimized.Finally,through experimental verification,it show that correlation calculation of non-corresponding side electrode couples can be realized effectively by the optimized multi-electrode electrostatic sensor,which lays a foundation for further research on velocity distribution measurement.

velocity distribution； sensor optimization； multi-electrode electrostatic sensor； effective correlation calculation

10.13873/J.1000—9787(2014)08—0087—03

2013—11—14

国家自然科学基金资助项目(61072101); 教育部新世纪优秀人才支持计划资助项目(NECT—10—0621) ; 天津大学自主创新基金资助项目

TP 212.1

A

1000—9787(2014)08—0087—03

王 超(1973- )，男，河北唐山人，教授，主要研究方向为电学层析成像、多相流测量和生物阻抗检测。