基于极限学习机的航空发动机传感器故障诊断*

孙毅刚， 刘静雅， 赵 珍

(中国民航大学 航空自动化学院，天津300300)

基于极限学习机的航空发动机传感器故障诊断*

孙毅刚， 刘静雅， 赵 珍

(中国民航大学 航空自动化学院，天津300300)

针对当前应用于航空发动机传感器故障诊断中的基于梯度的传统学习算法多存在参数选择困难、容易陷入局部最小化、过拟合等问题，提出了基于极限学习机(ELM)的航空发动机传感器故障诊断方法。算法只需设置隐含层神经元的个数，能够较好地避免上述问题，缩短故障诊断时间、提升诊断精度。通过仿真试验表明：基于ELM算法所建的航空发动机传感器故障诊断模型要比基于BP神经网络算法所建的模型耗时短且精度高。

极限学习机； 航空发动机； 传感器； 故障诊断

0 引 言

航空发动机故障是导致飞行事故的重要原因之一，严重影响着飞行安全[1],因此，亟需有效地提高航空发动机故障诊断的精度与效率，而航空发动机的诊断是建立在准确的传感器输出基础上的，所以，研究高效的航空发动机传感器故障诊断算法也是不容忽视的。近年来，BP神经网络与支持向量机(support vector machine, SVM)等多种方法被应用于航空发动机传感器故障诊断中，并且取得了一定成果[2～5]。但是BP神经网络在应用过程中需要对权重、阈值等大量参数进行设置，并且存在训练速度慢、易陷入局部极值、过拟合等问题。支持向量机尽管较BP神经网络运算时间短、精度高，但是其同样需要进行多参数的选择，如，核函数、惩罚系数、误差控制等。极限学习机(extreme learning machine,ELM)[6]是一种由单隐含层前馈神经网络(single hidden layer feedforward neural networks,SLFNs) 发展而来的新算法，该算法随机给定输入层与隐含层间的权值和隐含层神经元的阈值，只需对隐含层神经元的个数进行设置即可获得唯一最优解。该算法只包含简单的数学算法，学习速率较快，而且与传统的基于梯度的学习算法相比不易陷入局部最小化、过拟合等问题[6]。由于ELM算法有诸多优势，本文将ELM算法应用于航空发动机传感器的故障诊断中，并与基于BP神经网络算法得到的仿真结果做比较。

1 ELM算法机理

ELM是一种基于单隐层前馈神经网络的高效学习算法。与传统的神经网络相比，ELM算法随机产生输入权值和隐含层神经元的阈值，并且在整个训练过程中无需调整，只需设置隐含层神经元的个数，就可以获得唯一的最优解[7]，其网络结构如图1所示。

图1 ELM结构图Fig 1 ELM structure

图中wij表示输入层的第j个神经元与隐含层的第i个神经元之间的连接权值，βik表示隐含层的第i个神经元与输出层的第k个神经元间的连接权值，bi为第i个隐含层神经元的阈值，其具体形式如公式(1)

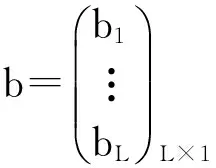
(1)

设给定任意N个不同的独立样本(xi,yi)，其中,xi=[xi1,xi2,…,xiN]T∈RN是一个N×1维向量，yi=[yi1,yi2,…yiM]T∈RM是一个M×1维的目标向量。对于具有L个隐含层神经元，激活函数为g(x)的前馈神经网络，其输出模型如式(2)

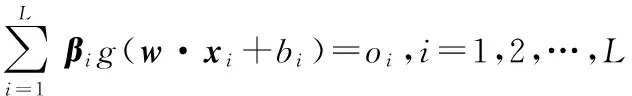
(2)

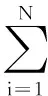
(3)

式(3)可简化为Hβ=Y，H为该神经网络隐含层的输出矩阵，其具体形式如式(4)所示

H(w1,…,wL,b1,…,bL,x1,…,xN)=

(4)

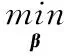
(5)

式中H+为隐含层输出矩阵H的广义摩尔逆(generalized Moore-Penrose inverse)。

由以上的分析可知，ELM在训练过程中随机给定输入权值w及隐含层神经元阈值b，通过计算求出β，其过程主要包括以下3个步骤：

1)确定隐含层神经元的个数，输入权值w和隐含层神经元的阈值b由系统随机产生。

2)选取一个无限可微的函数作为隐含层神经元的激活函数，求出隐含层的输出矩阵H。

3)计算输出权值β。

ELM在训练时无需调整过多的参数，只需设置隐含层神经元个数，根据相应算法来调整输出权值，在有限的时间内即可获得全局最优解。

2 航空发动机传感器故障诊断

本文提出的航空发动机传感器的故障诊断主要有离线建模和模型测试2个阶段，其原理图如图2所示。

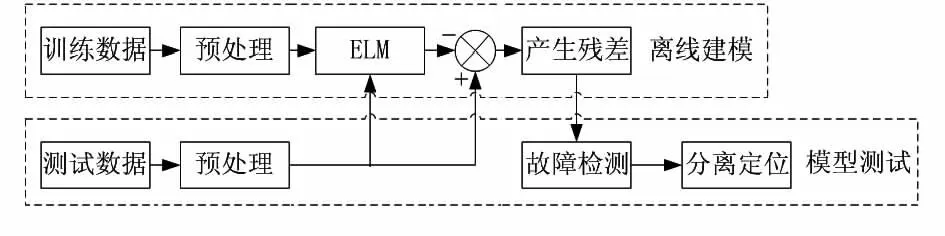
图2 传感器故障诊断原理图Fig 2 Principle diagram of sensor fault diagnosis

在离线建模阶段，需完成训练数据的预处理、训练ELM网络得出故障诊断模型2项工作。传感器直接的输出数据含有大量的噪声成分，需首先对数据进行小波去噪处理得到比较平滑的曲线，然后再将数据进行归一化处理，以提高建模的精度。数据归一化可采用最小—最大标准化的方法把数据变成[0,1]之间的小数，其公式为

新数据=(原数据-极小值)/(极大值-极小值).

(6)

在ELM的训练阶段可输入多组传感器数据训练得到网络的隐含层输出矩阵，进而通过式(5)得到输出权值，实现对单一的一组传感器数据的曲线拟合，拟合精度越高则代表建模精度越高。例如:可以应用温度、压力传感器的输出信号实现对转速信号的模型建立。

在模型测试阶段输入的是与训练数据不同的另一组测试数据，首先也需完成对测试数据的预处理，本文采用与训练数据相同的预处理方式，确保两类数据的处理精度是相同的。处理完后将数据输入已训练好模型，此时输入的测试数据要与相应训练过程中输入的不同传感器输出数据种类相一致，即训练时使用的哪几种传感器输出数据实现的对某一种单一传感器数据拟合，这里也要使用哪种传感器输出数据实现相应的输出。输入数据选择正确后，根据已有模型的输出权值实现对单一传感器测试数据的拟合工作，其模型输出值与此传感器的实际输出值是存在残差的，再根据残差值判断ELM模型的准确度并做进一步的故障检测，进而实现故障的分离与定位等后续故障处理等。

3 仿真试验

我国民航大型客机上都安装了快速飞行数据记录器(QAR)，QAR完整记录了发动机在飞行过程中的工作数据。本文采用了某架民航客机实际运行时记录的发动机数据，应用飞行高度(ALT)、油门杆角度(TLA)、发动机排气温度(EGT)、燃油流量(FF)信号对低压转子转速(N1)传感器信号进行仿真。

3.1 ELM激活函数的选择

激活函数影响着ELM算法的准确率，所以,选择合适的激活函数是很有必要的。算法的准确率采用网络的均方误差形式表示，即该输出值越小则准确率越高。本文分别选取了Sigmoid函数、硬限值函数(hardlim)、正弦函数(sin)、三角基传递函数(tribas)、高斯函数(radbas)5种比较常用的ELM激活函数，其对比图如图3、图4所示。

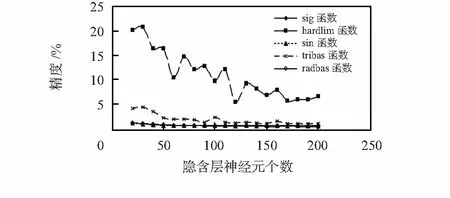
图3 不同激活函数训练精度对比图Fig 3 Training precision comparison chart of different activation function

图4 不同激活函数测试精度对比图Fig 4 Testing precision comparison chart of different activation function

图3、图4中，初始隐含层神经元个数均设置为10，之后以10为周期逐渐增加神经元个数。图3、图4均表明：Hardlim 函数极不适合应用于处理本数据，其输出值较其他激活函数大，即准确率低、误差大。图3中sig函数、sin函数、radbas函数精度曲线基本上为同一条曲线，可见这3种激活函数对算法的训练精度影响相近，且算法准确率较高。而图4中这3种激活函数对测试精度的影响则呈现了不同的状态，radbas函数随着隐含层神经元的增加输出值越来越大，准确率变低，而sin函数的输出也呈现了波动状态，相对来说，sig函数输出平稳，且输出值较小，准确率高，所以，本文选用sig函数作为ELM的激活函数。

3.2 ELM隐含层个数的选择

确定sig函数作为ELM算法的激活函数后，还要确定合适的隐含层神经元个数以使算法精度更高。初始隐含层神经元个数设置为20，之后以5为周期逐渐增加神经元个数，其结果如图5所示。由图5可知，随着隐含层神经元个数的增加，算法的训练精度值逐渐减小；而测试精度值则随之先减小后增加。因此，综合考虑训练精度、测试精度和训练时间，最终选定隐层神经元个数为80。

图5 隐含层个数对ELM精度的影响Fig 5 Effect of numbers of hidden layers on precision of ELM

3.3 本文算法与基于BP神经网络的方法比较

BP神经网络广泛用于传感器的故障诊断中，本文将其训练结果与ELM的训练结果相比较，突出ELM算法的优势。其训练效果对比如图6所示。

图6 基于ELM的算法与基于BP的算法训练效果对比图(数据1)Fig 6 Comparison diagram of training effect of ELM-based and BP-based algorithms(data 1)

图6(a)图为设置80个隐含层神经元个数时ELM算法实现的对数据的拟合，可见该算法误差值较小，能很好地拟合曲线。本文取原数据输出值的10 %做阈值，误差基本处于阈值范围内。图6(b)为在默认的BP神经网络下，设置隐含层神经元个数为4，用trainrp法对生成的网络训练10 000次后的训练结果，由图可知，此时BP神经网络已经达到一个较好的训练结果。这2种算法的训练时间和精度如表1，为比较直观，将精度采用百分数形式表示。

表1 基于ELM的算法与基于BP的算法训练结果对比(数据1)Tab 1 Comparison of training results of ELM-based and BP-based algorithms(data 1)

由表1可知，ELM算法不仅比BP神经网络算法精度高，而且速度较之要快几百倍，用ELM算法得到的模型能够更准确地用于故障诊断。由于飞机处于2个不同的飞行阶段变化时，如从巡航阶段过渡到下降阶段，或者同时伴有各种人为操作和环境对传感器性能的影响，使得传感器的输出值跳跃有时会比较大，因此，在这些阶段或者时间点上误差值相对较大，但是相对于传感器的输出值，其误差还是在可允许范围之内的。

本文针对训练出的模型，采用另一组数据进行了测试，其测试效果如图7所示。

图7 基于ELM的算法与基于BP的算法测试效果对比图(数据2)Fig 7 Comparison diagram of test effect of ELM-based and BP-based algorithms(data 2)

由图7可知，基于ELM的算法与基于BP的算法相比，在测试的初始阶段存在过拟合问题，但是后面的测试效果是比BP算法理想的。其测试时间与精度如表2所示。

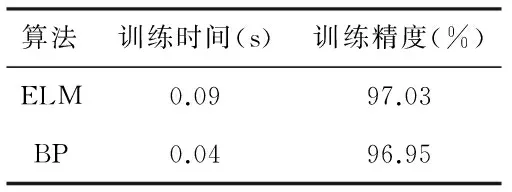
表2 基于ELM的算法与基于BP的算法测试结果对比(数据2)Tab 2 Comparison of test results of ELM-based and BP-based algorithms(data 2)

从表2可以看出：基于ELM的航空发动机传感器故障诊断方法的测试精度比基于BP神经网络航空发动机传感器故障诊断方法的测试精度更高，但由于ELM算法还需进行一些简单的运算，所以，其测试时间稍微长些。

4 结束语

本文提出了基于ELM的航空发动机传感器故障诊断方法。相比于BP神经网络的诊断方法，该方法只需设置隐层神经元的个数，不存在多参数选择困难，大大地缩短了航空发动机传感器故障诊断模型训练时间，且训练精度也有所提高。不过对测试数据初始阶段的拟合有待提高，可采用其他算法对ELM算法做进一步的优化。

[1] Tang G,Yates C L,Zhang J,et al.A practical intelligent system for condition monitoring and fault diagnosis of jet engines[C]∥35th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit,Los Angeles,1999：1-7.

[2] 何拥军,曾文英,曾文权.信息熵支持向量机算法传感器故障诊断研究[J].计算机仿真,2012,28(10):184-186.

[3] 神显豪.基于支持向量回归机的传感器故障诊断方法研究[J].机床与液压,2010,38(21):134-136.

[4] 郝 涛,唐永哲,任玉清.BP神经网络在飞控系统传感器故障诊断中的应用[J].计算机测量与控制,2008,16(5):613-615.

[5] 魏慕恒,贾秋玲.飞控系统传感器故障诊断的神经网络方法研究[J].自动化测试，2010,18(1):14-16.

[6] Huang G B,Zhu Q Y,Siew C K.Extreme learning machine:Theory and applications[J].Neurocomputing,2006,70(1-3):489-501.

[7] 史 峰,王 辉,郁 磊，等.智能算法[M].北京：北京航空航天大学出版社,2011.

[8] 陈立军,孙 凯,候媛媛,等.基于极限学习机的汽轮机故障诊断[J].化工自动化及仪表,2013,40(4):435-438.

Aircraft engine sensor fault diagnosis based on extreme learning machine*

SUN Yi-gang, LIU Jing-ya， ZHAO Zhen

(College of Aeronautical Automation,Civil Aviation University of China,Tianjin 300300,China)

Aiming at problems of traditional gradient-based learning algorithm used for aircraft engine sensor fault diagnosis always have currently,such as difficulties with multi-parameter selection, easy to fall into local minimum,over-fitting,and so on,propose fault diagnosis method for aircraft engine sensor based on extreme learning machine(ELM).ELM algorithm can avoid above problems,and further reduce fault diagnostic time and improve diagnostic precision,since it only need to set a parameter,i.e.the number of hidden layer.Simulation test shows that aircraft engine sensor fault diagnosis model based on ELM algorithm has higher precision and shorter time than that based on BP neural network algorithm.

extreme learning machine(ELM); aircraft engine; sensor; fault diagnosis

10.13873/J.1000—9787(2014)08—0023—04

2014—01—10

国家自然科学基金委员会和中国民用航空局联合研究基金重点资助项目(U1233201)；天津市科技支撑计划重点资助项目(11ZCKFGX04000)；中央高校基本科研基金资助项目(ZXH2012B002，3122013P005)

V 233.7

A

1000—9787(2014)08—0023—04

孙毅刚(1963-)，男，山东汶上人，博士，教授，研究方向为智能控制、传感器故障诊断。