表面缺陷对波导丝中的扭转波传播影响研究

周泓辰， 周翟和， 汪 炜

(1.南京航空航天大学 机电学院，江苏 南京 210016；2.南京航空航天大学 自动化学院，江苏 南京 210016)

表面缺陷对波导丝中的扭转波传播影响研究

周泓辰1， 周翟和2， 汪 炜1

(1.南京航空航天大学 机电学院，江苏 南京 210016；2.南京航空航天大学 自动化学院，江苏 南京 210016)

波导丝是磁致伸缩位移传感器的核心元件，其表面质量直接影响传感器的测量精度。为研究波导丝表面质量对检测信号的影响规律，通过建立扭转波在波导丝中传播的力学模型，得到扭转波的波动方程。在此基础上，对2种不同表面状况下波导丝中扭转波的传播开展数值模拟和实验验证。研究结果对今后高精度大量程磁致伸缩位移传感器的研制具有一定参考作用。

磁致伸缩； 波导丝； 扭转波； 数值模拟

0 引 言

作为新型传感器，磁致伸缩位移传感器具有精度高、量程大、非接触测量、能在高振动、高温、高压、大粉尘恶劣环境中使用等诸多优点，因而,受到了石油化工、自动控制、航空、水利等众多行业的青睐[1～3]，在我国的工业生产中得到了广泛应用。

磁致伸缩位移传感器的核心元件是磁致伸缩材料制成的波导丝。作为承载扭转波信号传播的关键介质，波导丝的表面质量直接影响传感器的测量精度。目前，通常采用实验方法研究波导丝对扭转波信号的影响[4]。

本文从扭转波传播的波动模型出发，利用ANSYS和Matlab软件对不同表面质量下波导丝中扭转波的传播过程进行数值分析，并对结果进行了实验验证，为磁致伸缩位移传感器的研究提供了另外一种思路。

1 磁致伸缩位移传感器的原理

磁致伸缩位移传感器是利用威德曼效应研制的传感器。威德曼效应[5,6]是指磁化使铁磁材料产生机械应变的效应。传感器原理如图1 所示。

图1 传感器原理图Fig 1 Principle of sensor

敏感元件是一根波导丝[7～9]，波导丝由磁致伸缩材料制成。测量过程是由传感器的电子仓产生一个周期性的电流脉冲，该电流脉冲在波导丝内传输，从而在波导丝外产生一个环形磁场[10,11]。当该磁场与套在波导丝上作为位置变化的活动磁铁产生的轴向平行磁场相交时，两者叠加产生一个螺旋形磁场。由于波导丝的磁致伸缩特性，该处波导丝内会产生一个应变扭转波信号，这个应变扭转波信号以固定的速度向两边传播，然后通过扭转片被检测线圈[12]检测到。线圈中信号的瞬时电动势εt为

(1)

其中,n为检测线圈匝数，r为线圈有效半径，θ为线圈横截面与磁感线的夹角，ΔB/Δt为磁通密度变化率。通过测量激励脉冲与扭转波信号的时间间隔，就可以确定活动磁铁目前的位移。由于输出信号是一个真正的绝对值，而不是比例的或放大处理的信号，所以,不存在信号漂移或变值的情况，无需定期标定。

2 力学模型

波导丝在螺旋形磁场的作用下发生磁致伸缩应变，从而在内部激发了应力波，亦可称为弹性导波。弹性波沿波导丝传播时，可分为三种模态：纵向模态、扭转模态和弯曲模态。因为理想的螺旋形磁场是轴对称的，根据导波理论，弯曲模态可以忽略不计。一般的超声波传感器总是利用纵波来实现测量目的。相对于纵波，扭转波的回波较弱，但扭转波脉冲能以较小的失真和波偏移沿波导管传递较长的距离，而且不易受外部冲击或振动所干扰[13]。在磁致伸缩位移传感器中，受螺旋形磁场的作用，波导丝中的扭转波的强度远大于纵波脉冲。如果利用纵波实现测量目的，为获得足够强的信号，必须用线圈取代磁环，在使设计复杂化的同时也使可靠性下降。因此，磁致伸缩位移传感器主要利用扭转波实现测量目的。下面对波导丝中扭转波进行建模分析。

如图2所示为长度为dx的等截面波导丝单元，θ为扭转角，T为扭矩，I为极惯性矩，ρ为材料密度，G为材料剪切模量。假设波导丝变形时横截面始终保持为平面，通过假设，各个运动参量都可以简化为x和时间t的函数。扭矩与扭转角的关系为

(2)

图2 波导丝单元受力分析图Fig 2 Analysis of waveguide wire unit

由动量矩定理可得

(3)

即波导丝中扭转波传播的波动方程为

(4)

3 数值模拟和实验研究

目前，工业生产中波导丝是由合金棒材经初拉、中拉、细拉等20多次工序制备出来的[14]。与理想状态下相比，由于工艺不完善和运输过程中的碰撞，波导丝极易出现颈缩、划伤等表面缺陷，本文选取由于颈缩而产生的凹陷现象来研究表面缺陷对信号的影响。

波导丝的表面缺陷增加了信号检测的困难度和不确定性。为确定波导丝表面缺陷对扭转波传播的影响，进行如下工作：

1)分别对波导丝表面无缺陷、凹陷二种状况，进行有限元分析；

2)进行实际实验，人为制造波导丝缺陷，获得上述二种状况时的信号状态；

3)针对分析和实际结果，进行对比分析。

3.1 扭转波的有限元分析

波导丝中扭转波传播的有限元分析采用的是瞬态动力学方法，通过对特定节点施加随时间变化的位移载荷来模拟波导丝受激产生的扭转波。

波导丝材料为具有磁致伸缩特性的铁镍合金，材料密度ρ为8 000kg/m3，弹性模量E为191GPa，泊松比μ为0.34，磁致伸缩系数λ为40×10-6。本文取波导丝的一小段进行分析，模型直径D为0.8mm，长为100mm，缺陷处直径为0.6mm。

Bridgman、陈篪等人用实验方法求得圆柱式样拉伸产生的颈缩外形比较符合双曲线[15]。整理数据可得，在如图3所示坐标系下双曲线公式为

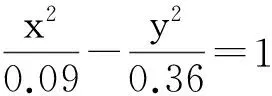
(5)

设a点坐标为(0.4,ya)，带入上式可得ya=0.529mm,即缺陷宽度约为2ya=1mm。

因波导丝长径比较大，可将其简化为一维模型，选取梁单元BEAM188进行网格划分。波导丝表面无缺陷、凹陷二种状况下的模型参数如图3所示，凹陷距波导丝左端面19mm，凹陷处直径为0.6mm，宽为1mm。

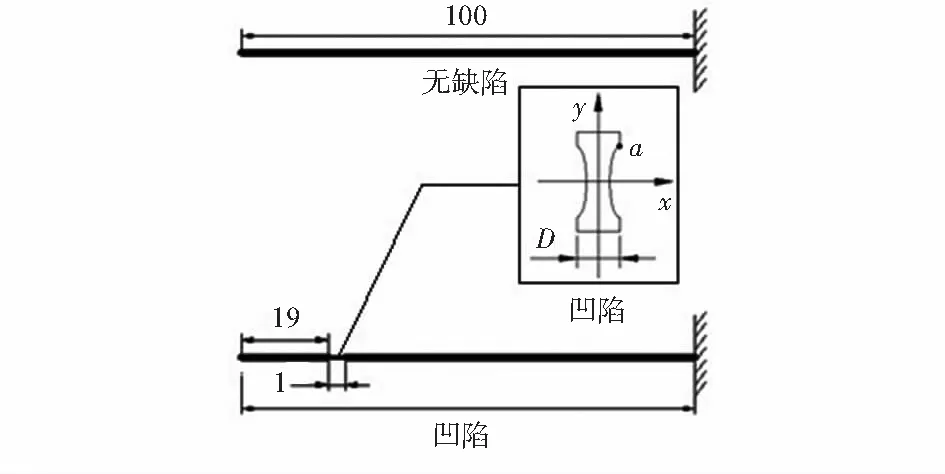
图3 波导丝模型参数Fig 3 Parameters of waveguide wire model

扭转激励载荷选取经汉宁窗调试的5 MHz正弦波信号。因磁影响宽度w为40 mm，信号幅值a为

a=2λwμ/D=1.36×10-3.

(6)

信号函数为

(7)

式中 λ为磁致伸缩系数，μ为泊松比，D为波导丝直径，τ为汉宁窗的截取宽度，取正弦信号的6个周期为1.2μs，信号波形如图4所示，汉宁窗调制可消除高频干扰与能谱泄漏，相对于正弦波其频带宽，脉冲相对窄，纵向分辨率高。

图4 激励信号Fig 4 Excitation signal

因是研究缺陷对扭转波传播的影响，所以，分别对图3所示波导丝左端面及距左端面35 mm处节点施加激励载荷。取距波导丝左端面40 mm处为波形拾取装置的焊接位置，选取该位置节点进行研究，在时间历程后处理器中导出数据，利用Matlab进行处理，节点获得的波形结果如图5所示。

图5 距左端面40 mm处节点波形Fig 5 Waveform of node which is 40 mm away from the left end

当振源在缺陷之前时，扭转波信号在被信号拾取装置拾取之前不需经过缺陷处。对比图5(a)中两幅图，缺陷对信号幅值无影响，但会在其后形成一个小的反射波。

当振源在缺陷之后时，扭转波信号必须经过缺陷才能被信号拾取装置拾取。对比图5(b)中两幅图，扭转波经过缺陷后，信号频率发生弥散，幅值有一定程度的降低。

3.2 实验与结果分析

有限元分析只是在理想条件下对实际情况的模拟，还需要与实验进行对比验证。实验中波导丝材料为铁镍合金，直径为0.8 mm，在距信号拾取装置42 cm处人为制造一处缺陷，对比前后磁环在同一位置时的信号。扭转波信号经拾取，放大滤波后的波形如图6所示。

由图6可见，磁环在缺陷前时，信号幅值不受影响，缺陷处形成一小反射波；磁环在缺陷后时，信号幅值衰减严重。实验结果与仿真结果近似。

图6 拾取信号波形图Fig 6 Waveform of the picked-up signal

缺陷引起的反射波和幅值衰减会对后续的信号处理和时间检测带来很大麻烦。但缺陷引起的反射波也可以被利用来确定缺陷的位置：如图6(a)中可以读出扭转波与反射波之间的时间间隔t，由扭转波波速v可得缺陷与磁环的距离为s=vt/2。确定缺陷位置之后可以直接去除波导丝的缺陷部分或者通过算法设计消除缺陷带来的影响。

4 结 论

本文通过波导丝的振动方程和有限元分析两方面入手，分析了波导丝中扭转波在有无缺陷二种情况下的传播过程。同时，通过实验获得实际中二种情况下的信号波形图，验证了有限元分析结果与实验结果的一致性。该分析方法和结果，可作为缺陷分析以及大量程磁致伸缩位移传感器设计的参考。

[1] 李春楠,卢 云,兰中文,等.磁致伸缩位移传感器的研究进展[J].实验科学与技术,2008(2):10-12.

[2] 美国MTS系统公司.磁致伸缩位移传感器的技术与创新[J].传感器世界,1997(11):15-231.

[3] 李怀洲,孙海燕,罗祖顺,等.磁致伸缩位移传感器的研究与应用[J].电气自动化,2005,27(5):58-59.

[4] 柴婷婷.磁致伸缩位移传感器检测信号的实验研究[J].测试测量技术,2008(6):8-11.

[5] Pulido E,Real R P del.Amorphous wire magnetic field and D.C.current sensor based on the inverse Wiedemann effect[J].IEEE Transactions on Magnetics,1991(27):5241-5243.

[6] Hristoforou E,Niarchos D.Amorphous wires in displacement sensing techniques[J].Journal of Magnetism and Magnetic Materials,1992(116):177-188.

[7] Hristoforou E,Chiriac H.On the calibration of position sensor based on magnetic delay lines[J].Sensors and Actuators A,1997(59):89-93.

[8] Chiriac H,Marinescu C S.New position sensor based on ultraacoustic standing waves in FeSiB amorphous wires[J].Sensors and Actuators A,2001(81):174-175.

[9] Karagiannis V,Manassis C,Bargiotas D.Position sensors based on the delay line principle[J].Sensors and Actuators A,2003(106):183-186.

[10] Wakiwaka H.Displacement sensor using magnetostrictive wire and decrease of its hysteresis error[J].Sensors,2008(21):379-384.

[11] Affanni A,Guerra A.Design and characterization of magnetostrictive linear displacement sensors[C]∥Instrumentation and Mea-surement Technology Conference,Como,Italy,2004:206-209.

[12] Hristoforou E,Niarchos D.A coily magnetostrictive delay line arrangement for sensing applications[J].Sensors and Actuators A,2001(91):91-94.

[13] 杨维明.超声波导位移传感器的研究[J].沈阳工业大学学报,1991,13(3):43-49.

[14] 申 蓉,卢 云,冯哲圣,等.热处理对磁致伸缩波导丝性能的影响[J].功能材料,2009,40(6):918-919.

[15] 嵇 醒,殷家驹,汤 泉.颈缩的有限元分析[J].固体力学学报,1983(4):532-542.

Research on influence of surface deficiency on propogation of torsional wave in waveguide wire

ZHOU Hong-chen1, ZHOU Zhai-he2, WANG Wei1

(1.College of Mechanical and Electrical Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China; 2.College of Automation Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China)

The waveguide wire is the key component of magnetostrictive displacement sensor,its surface quality directly influences measurement precision of sensor.In order to research influence rule of surface waveguide wire on detecting signal,wave equation is achieved by establishing mechanical model of torsional wave propagation in waveguide wire.On this basis,propagation of torsional wave in two different surface quality of waveguide wire is investigated by using numerical simulation and experimental verification.Research results has certain reference effect on development of magnetostrictive displacement sensor with wide-range and high-precision.

magnetostrictive; waveguide wire; torsional wave; numerical simulation

10.13873/J.1000—9787(2014)08—0011—04

2014—01—08

TP 212.1

A

1000—9787(2014)08—0011—04

周泓辰(1989- )，男，江苏盐城人，硕士研究生，主要研究方向为传感器设计与制造。