基于径向基神经网络的舰艇空间磁场延拓*

谢志强 连丽婷

(91388部队 湛江 524022)

基于径向基神经网络的舰艇空间磁场延拓*

谢志强 连丽婷

(91388部队 湛江 524022)

针对目前线性化方法解决舰船空间磁场之间推算时存在的困难,论文从智能优化的角度出发,建立了舰艇空间磁场之间的径向基神经网络预报模型。该方法避免了利用线性化方法存在的诸多困难,即可实现舰艇空间磁场的换算,并利用船模实验验证了网络预测的准确性,换算精度较高,满足工程实际需求。

舰艇; 磁场; 内外推算; 神经网络; 径向基函数

Class Number TM153.1

1 引言

磁隐身技术对于潜艇来说是至关重要的。随着国内外磁探潜技术的日新月异,也给潜艇的磁隐身技术提出了更高的要求。潜艇的磁场是容易被敌方侦测到的重要物理场[1],现代的反潜飞机大部分是通过声纳探测发现目标,通过磁探测来精确定位,因此如果能够掌握潜艇水下某一深度处磁场与高空某一高度处磁场之间的关系,进而有效地实行磁性防护,例如消磁手段,既能有效地防止水下磁性武器的攻击,又能有效地抵御高空磁探,增加潜艇的作战能力。

近年来,磁场数值建模技术在舰艇磁隐身中得到了广泛的研究,主要的方法有有限元法、边界元法、积分方程法和磁体模拟法[2～6]。现有方法主要从线性建模的角度出发来解决磁场推算问题,不可避免地会存在复杂的磁性结构重构、剖分或复杂的重积分求解等问题,随着大型舰船的不断加入现役,将会加剧线性化处理的难度,影响其换算精度。近年来,神经网络技术得到广泛应用[7～8],本文从智能优化的角度出发,建立了水下磁场与空间磁场之间的径向基神经网络预报模型。该方法避免了利用线性化方法存在的诸多困难,即可实现舰艇空间磁场之间的换算,并利用船模实验验证了网络预测的准确性,相较于其他线性化方法,其换算精度有所提高,满足工程实际需求。

2 舰船空间磁场换算的线性数学模型

从磁源的理论出发,舰船空间磁场均是由磁源产生的,只是空间场点位置相对于磁源而言不同而已,如图1所示。

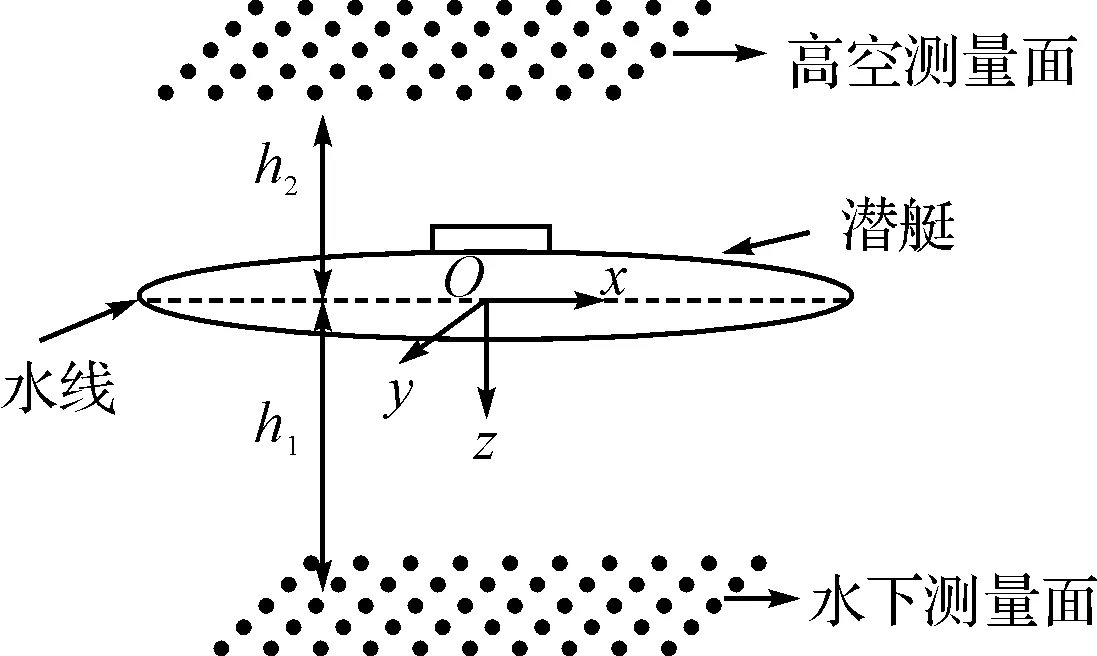
图1 舰艇空间磁场换算示意图

假设选择磁偶极子作为虚拟磁源,根据文献[6],单个磁偶极子在周围空间产生的磁感应强度B可用下式表示:

(1)

其中m代表磁偶极子的磁矩,r代表代表源点到场点的矢径,方向由磁偶极子中心指向计算场点。假设舰船用k个磁偶极子模拟,测量点数为n,如图2所示,则第i个磁偶极子在测量点P处产生的磁感应强度三分量可用下式表示:

(2)

其中xp、yp、zp分别代表水下测量点P的坐标三分量,x0、y0、z0分别代表磁偶极子中心的坐标三分量,rp代表第磁偶极子中心到测量点p的矢径,如图2所示。写成矩阵形式为A·M=B,其中M代表磁矩矩阵,B代表磁感应强度测量值组成的列向量,A为联系等效磁矩和磁感应强度测量值的线性观测矩阵,矩阵中的每个元素由场点和测量点的坐标决定。式(2)对于舰船空间磁感应强度值计算都是适用的。可以通过测量得到的水下某一深度处的磁感应强度反演出等效的磁矩列向量M,再正演出舰船上方某一高度处的磁感应强度值。

图2 磁偶极子及测量场点图

3 RBF神经网络的基本原理

RBF神经网络是一种具有单隐层的三层前馈网络[9～10],它模拟了人脑中局部调整、相互覆盖接受域的神经网络结构,由输入层、具有径向基函数神经元的隐层和具有线性神经元的输出层构成,如图3所示为一个典型的RBF神经网络结构图。径向基层单元的作用函数常取高斯基函数,可表示为:radbas(n)=e-n2。神经元radbas的输入为输入向量p与隐层权值w1之间的距离(dist函数)与隐层阈值b1的乘积;输出层神经元传递函数为purelin,输出层权值为w2,输出层阈值为b2。选择Matlab工具箱中的newrb()函数设计网络,该函数包含输入样本、期望输出、训练精度Goal和散布常数spread几个关键变量。其中散布常数的选择尤为重要,如果散布常数选择不当,会造成网络设计中神经元数过多或过少,进而在函数逼近中造成过适性或不适性,一般情况下,散布常数的选取取决于输入向量之间的距离,要求是要介于最小距离与最大距离之间。

图3 径向基网络结构图

4 神经网络在舰艇空间磁场推算中的应用

4.1 潜艇感应磁场换算实验设计

为了获取神经网络的学习样本与测试样本,而相较于舰艇的固定磁场,感应磁场更加容易获取。分别在一潜艇模型水线下方h1=36.8cm与水线上方h2=40.8cm处布设传感器阵列,如图4所示,分别选取模型两个测量面的龙骨处即测量线1、2处的磁场值作为样本集,为了减小测量误差,测量模式采用船模运动、传感器固定的方式,由其相对运动而测量得到不同场点的磁场值。感应磁场采取南北航向分别测量,测量点数为32(测量点从南至北标号为1～32),测量间距为10cm。

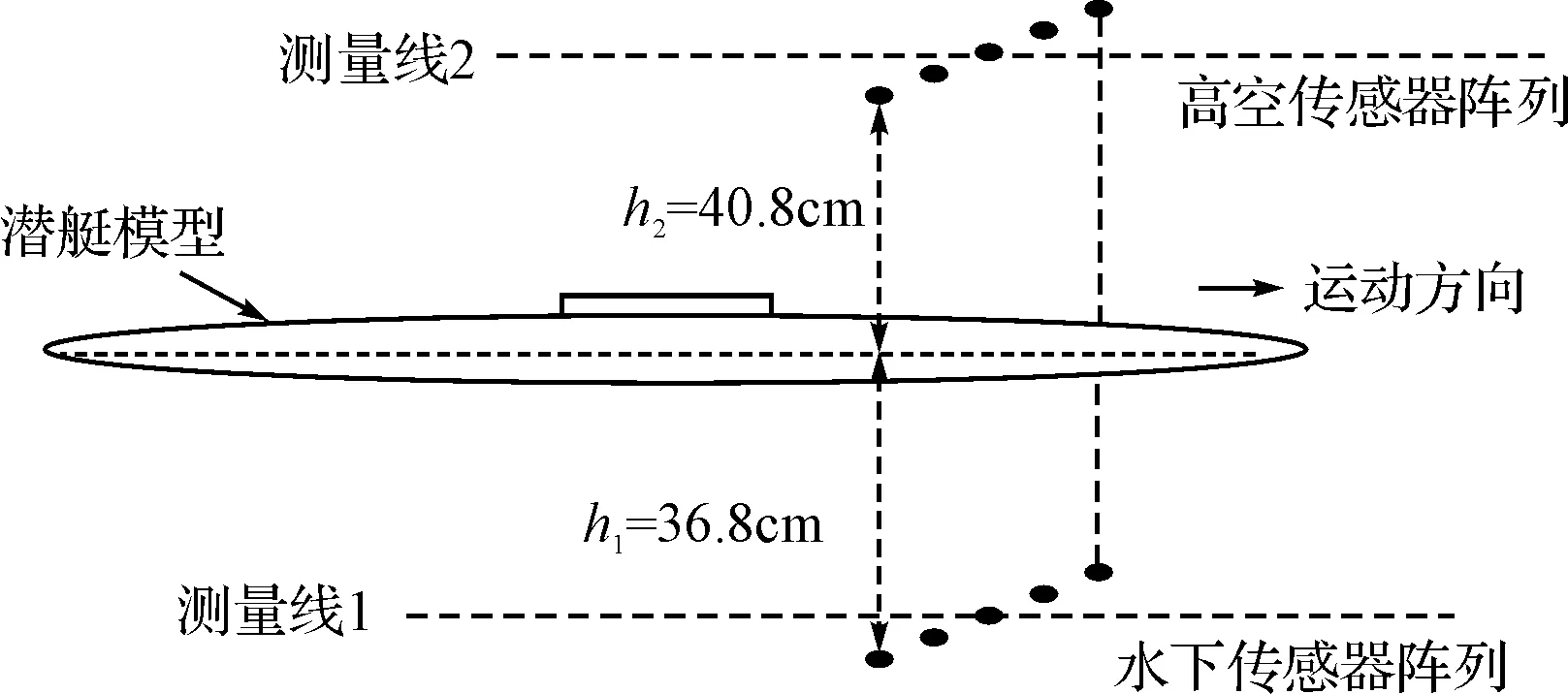
图4 传感器布设图

4.2 RBF网络基本参数的确定

将实验获取的南北航向磁场值相减,取其平均值,则选取测量数据所对应奇数组内外测量数据作为A组,偶数组内外测量数据作为B组。则RBF神经网络的基本参数选取规则如下:

训练样本集:选取A组中的内部测量数据作为训练网络的学习样本,A组中的外部测量数据作为训练网络的期望输出;

测试样本集:选取B组中的内部测量数据为测试网络训练效果的输入样本,B组中的外部测量数据作为网络的理想输出;

训练精度Goal:Goal=0.00001;

散布常数spread:0.001。

4.3 网络训练以及网络评价

基本参数设置好后,输入学习样本,训练网络,并输入剩余的测试样本来测试网络的预测准确性,并将网络的预测值与外部磁场的实际测量值进行比较,如图5所示为磁场数值归一化后预测值与测量值比较图,由图可见,磁场预测值与测量值吻合较好。选取最大相对误差作为衡量预测精度的判定依据。其网络预报误差控制在5%内,相较于传统方法误差控制在10%以内,精度有所提高,且具备较好的稳定性。

图5 网络预测值与测量值比较图

5 结语

本文先从线性化角度研究了舰船空间磁场之间的关系,利用线性化方法建模会存在复杂的磁性结构重构、剖分或复杂的重积分求解等问题,且随着舰船的大型化、复杂化、铁磁设备多样化,均会加剧其难度,进而影响换算精度。鉴于此,本文从智能优化的角度出发,提出了一种基于径向基神经网络预报模型,通过设计的船模实验验证了网络预测的准确性,其换算精度不低于95%,符合工程实际需求。

[1] 张维俊.舰船隐身面临的挑战和技术发展展望[J].中国舰船研究,2007,2(6):46-49.

[2] 周国华,肖昌汉,等.一种舰艇磁隐声中磁场推算的新方法[J].兵工学报,2009,30(7):951-956.

[3] 王金根,龚沈光等.磁性目标的高精度建模方法[J].海军工程大学学报,2001,13(3):49-52.

[4] Liu Sheng-dao, Liu Da-ming, Xiao Chang-han, et al. Magnetic model of magnetic objects based on genetic algorithm[C]//The 6thInternational Conference on Electromagnetic Field Problems and Applications. San Antonio: TSI Press,2008:51-54.

[5] 高峻吉,刘大明,姚琼荟.舰船固定磁性分解方法研究[J].哈尔滨工程大学学报,2007,28(10):1164-1170.

[6] 周耀忠,张国友.舰船磁场分析计算[M].北京:国防工业出版社,2004:194-195.

[7] 董长虹.Matlab神经网络与应用[M].北京:国防工业出版社,2007:64-110

[8] ZHOU G H, XIAO C H, LIU S D. Magnetic moments estimation and localization of a magnetic object based on Hopfield Neural Network[C]//The Proceeding of the 6thInternational Conference on Electromagnetic Field Problems and Application, San Antonio,2008.

[9] 耿志强,朱群雄,顾祥柏,等.基于多群竞争PSO-RBFNN的乙烯裂解深度智能优化控制[J].化工学报,2010,61(8):1942-1948.

[10] 张利平,孙美凤,王铁生.新型的RBF神经网络在水轮发电机组故障中的应用[J].水力发电学报,2009,28(6):219-224.

Magnetic Anomaly Extrapolation of Submarines Based on Neural Network

XIE Zhiqiang LIAN Liting

(No. 91388 Troops of PLA, Zhanjiang 524022)

Magnetic anomaly created by ferromagnetic ships may make them vulnerable to detections and mines. In order to reduce the anomaly, it is important to evaluate magnetic field firstly. Underwater field can be measured easily, but upper air field is hard to be got. To achieve it, a model able to predict upper air magnetic field from under-water measurements is required. In this paper, a Radial Basis Function(RBF) neural network model is built to solve it. The method can avoid many problems from linear model and its high accuracy and good robustness are tested by a mockup experiment.

ship, magnetic field, magnetic field extrapolation, neural network, radial basis function

2013年7月4日,

2013年8月29日

谢志强,硕士,工程师,研究方向:水下目标模拟技术。连丽婷,博士,工程师,研究方向:水下目标模拟技术。

TM153.1

10.3969/j.issn1672-9730.2014.01.043