热储分层影响EGS采热的数值模拟研究*
2014-07-01黄文博陈继良蒋方明
黄文博,陈继良,蒋方明
(中国科学院广州能源研究所,中国科学院可再生能源重点实验室,先进能源系统实验室,广州 510640)
热储分层影响EGS采热的数值模拟研究*
黄文博,陈继良,蒋方明†
(中国科学院广州能源研究所,中国科学院可再生能源重点实验室,先进能源系统实验室,广州 510640)
由于岩石构造不同、天然裂隙的差异以及压裂过程的随机性等因素,增强型地热系统(EGS)人工热储通常具有较强的非均质性。探究热储的非均质性对EGS热开采过程的影响,对EGS性能预测与分析评价有重要意义。论文考虑到热储沿深度方向的非均质性,基于等效分层多孔介质物理模型,并使用自主开发的EGS数值模型,模拟了多个具有分层热储EGS的长期运行过程,发现热储深度方向上非均质性对热能的开采影响显著,而流量分布的不均匀性是导致系统采热性能下降的主要原因。为了方便分析和评价,我们建立一种新的定量化描述热储非均质性的方法,然后基于更多的非均质热储EGS算例结果,拟合得到EGS采热性能与热储非均质性的定量关系式。
增强型地热系统(EGS);数值模拟;等效分层多孔介质;非均质性
0 前 言
在地下3~10 km的低渗透性岩石中储存着大量的热能。为了有效地开发利用这些热能,美国拉斯阿莫斯国家实验室(Los Alamos National Laboratory)在 1970年提出了增强型地热系统(Enhanced Geothermal Systems, EGS)概念——通过水力压裂、化学腐蚀等方法增加地下深层岩石的渗透性形成人工热储,然后建设流体循环系统,经由注入井注入冷流体工质,其在人工热储被加热后由采出井输送至地面电厂,发电后的流体经进一步的梯级利用后再灌注到地下热储,循环利用,从而实现深层地热能的持续开采[1]。EGS不仅具有常规水热型地热供能稳定持续且污染物排放量小的优点,同时还具有储量巨大、分布广泛的特点,有望成为未来能源中的重要组成部分[1-5]。
人工热储的建立是 EGS建设过程中的关键环节,水力压裂是通常采用的方法。该方法通过往深层岩石中持续注入高压液体,压裂岩石或使岩石中的天然裂缝发生扩张和延伸,形成结构复杂的裂隙网络,增加岩石的渗透性[1]。由于岩石构造不同、天然裂缝的差异以及压裂过程的各种不确定性因素,热储区域裂隙网络往往具有很强的非均质性[6-10]。热储的裂隙结构直接影响流体在热储中渗流换热过程,是决定热储可开采热能和EGS寿命的关键因素。评估热储裂隙网络的非均质性对EGS采热性能的影响,可为人工热储的压裂激发过程提供指导,对提高EGS经济性具有重要意义。
数值模拟作为一种成本低、效率高并且功能强大的研究方法,在当前的EGS研究工作中得到了广泛的应用。EGS数值模拟中,根据对裂隙网络处理方式的不同,热储模型大致可分为两类[11,12]:离散裂隙模型(Discrete Fracture Network Model, DFN)和连续介质模型(Equivalent Continuum Model)。离散裂隙模型严格地区分岩石骨架和裂隙,可以很好地体现裂隙开度、裂隙空间分布等因素对流体流动和换热的影响。但是EGS热储尺寸通常为裂隙尺寸的105~106倍,对于实际的EGS热储,DFN会因计算量过大难以进行。连续介质模型基于等效体积(Representative Equivalent Volume, REV)平均的假设,即使用体积平均性质来近似描述热储局部的各种性质,可以在未探明热储内裂隙网络的具体几何形态和空间分布的情况下对热储进行较为准确的宏观等效描述,计算量相对较小,是目前EGS数值模型中主要使用的方法。
在连续介质模型中,根据对热储参数的设定方法的不同,等效多孔介质又可分为单孔隙度模型(Single-porosity Model)[13-16]、双孔隙度模型(Double-porosity Model)[17-20]和多孔隙度模型(Multi-porosity Model)[21-26]三种。
由于热储位置通常在地下数千米,获得精确描述不均匀热储的结构信息在目前来看依然十分困难,很多文献中采用了单孔隙度模型。这种模型将热储视为均匀热储,认为热储中的地热地质参数大致为该区域的平均值。单孔隙度模型通常用于检验EGS数值模型的适用性[13],也可以在一定程度上对EGS宏观运行规律进行研究[14-16]。由于这种模型忽略了热储的非均质性,难于真实反映热储中的渗流过程,对实际EGS系统运行情况的预测会有偏差。
为了较好地体现实际热储中的结构,一些研究者采用了双孔隙度模型。双孔隙度模型仍视热储为多孔介质,但它将每个热储单元划分为两类子域:低孔隙率的岩石骨架和高孔隙率的裂隙。在双孔隙度模型基础上,多重连续介质(Multiple Interacting Continua, MINC)模型对双孔隙度模型中区别明显的两个子区域进一步划分,避免在局部地区产生过大的物理量梯度,使得计算更趋稳定。以MINC模型为基础的 TOUGH软件目前得到了广泛的应用[19,20],但双孔隙率模型面临岩石骨架和裂隙区域如何划分、如何根据野外地质勘测和实验数据区别设置两区域的参数等困难。
为了更好地把实地勘测的数据反映到热储模型中,一些研究者采用了多孔隙度模型。Kalinina等[21]、 Shaik等[22]将裂隙方向、间距、开度和长度等重要裂隙参数都考虑进模型中,进而构建出孔隙度、渗透率的空间分布;Vogt等[23,24]尝试通过 EnKF(Ensemble Kalman Filter)和蒙特卡洛方法(Monte Carlo approach),依据示踪剂循环实验等实测结果重构出渗透率在热储中的分布情况。但是,由于难以获得足够多的精确地质数据,目前多孔隙度模型仍不足以还原真实EGS热储复杂的裂隙结构。
Fourar[25]提出了用等效 分 层 多孔介质(Equivalent Stratified Porous Medium)来描述不均匀热储。这种模型将热储假设为分层结构,各个流动层具有不同的渗透性,并且认为热储中的流动平行于流动层。Radilla等[26]尝试将该模型用于解释法国苏尔士(Soultz)地区EGS热储结构,其计算结果与示踪粒子实验结果吻合很好。Blöcher等[27]将分层多孔岩石储层模型应用于模拟深层地热储池内水热过程。最近,Luo等[28,29]还将分层热储模型用于CO2-EGS采热过程[28]和CO2地质存储[29]的模拟。
本文将EGS热储考虑成多个单孔隙度流动层,通过设定各流动层的孔隙度、渗透率等宏观参数来模拟构建沿深度方向的不均匀热储,基于对EGS的长期采热过程的数值模拟结果,研究热储深度方向的非均质性对EGS采热性能的影响。本文将在详细分析热储渗流分布对EGS采热性能影响的基础上,定义合理的描述热储非均质性参数;同时,将提出相对采热率的概念并采用其评价不均匀热储EGS的采热性能;另外,还将采用随机方法构建30个分层不均匀热储并模拟EGS长期运行,继而通过分析数值结果确定分层热储结构下EGS采热性能与热储非均质性的定量关系。
1 数学-物理模型
1.1 物理模型
考虑典型EGS双井布局,EGS的地下部分由井、人工热储和热储周围的干热岩三个部分组成。在数值计算中,忽略热储周围岩石的渗透性,注入井和生产井均视为开放式流体通道。如图1所示,Region 1代表分层热储,Region 2为热储周围不可渗透的岩石,Region 3为注入井和生产井。
该模型对热储进行了以下假设:(1)热储视为分层结构;(2)每个流动层都视为均匀单孔隙度介质。对于实际EGS热储,一般只有2~3分层[26],本文将热储沿深度方向等分为10个水平流动层。
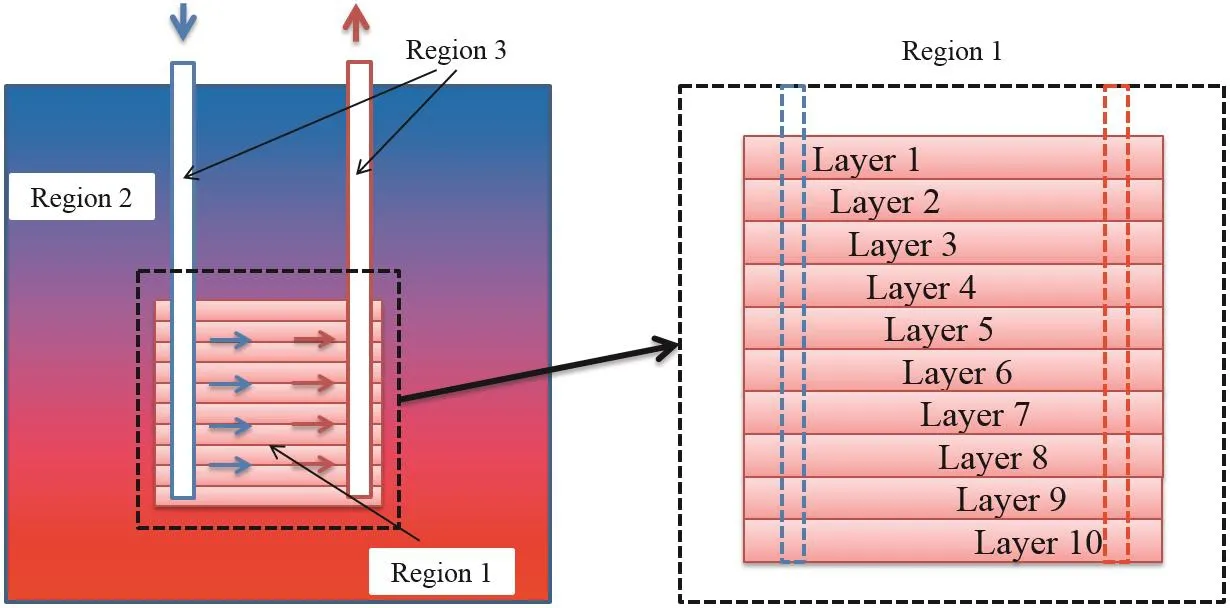
图1 EGS地下部分和分层热储的物理模型Fig. 1 Physical model of EGS subsurface part and stratified reservoir
1.2 数学模型
对于EGS采热过程的模拟,我们采用了前期自主开发的三维模型[13]。该模型为了模拟热储中的局部对流换热,基于局部非热平衡思想[30],采用两个能量方程来分别描述流体和岩石的温度变化过程。模型的主要假设如下:
(1)单相流体流动;
(2)初始时刻,热储孔隙中充满采热流体;
(3)忽略循环流体的损失量(fluid loss);
(4)不考虑循环流体与岩石的化学反应;
(5)忽略岩石热应变及流体压力导致的热储孔隙度的变化。
模型的主控方程有连续性方程、动量方程、流体的能量方程和岩石的能量方程。
连续性方程:

动量方程:

流体的能量方程:
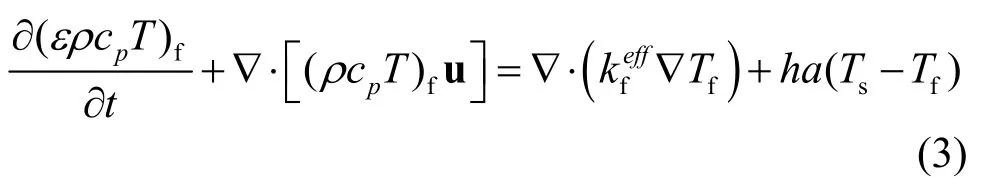
岩石的能量方程:

其中,ε为热储孔隙度,ρ为密度,cp为比热容,u为流体表观速度,P为流体压力,μ为流体动力粘性系数,K为热储渗透率;热储中岩石和流体的有效导热系数使用修正因子为1.5的Bruggeman关系式来确定,即和h代表热储中固体岩石和流体间的对流换热系数,a为裂隙的比表面积,可依据平板裂隙结构或圆管直通道来估测h和a的数值[17],研究中取ha=10 W/(m3·K)。
2 算例设置
2.1 模型参数
双井EGS的几何参数如图2所示。人工热储的体积为500 m × 500 m × 500 m的正方体,计算区域大小为1 000 m × 1 000 m × 1 500 m,为减少人为边界条件设置对结果带来的影响,热储周围包覆有足够体积的岩石。注入井和生产井均为0.2 m × 0.2 m的方形通道。模型的求解借助Fluent通用计算流体力学软件提供的求解平台,通过其灵活的UDF(User Defined Functions)进行编程并数值求解。因几何对称,仅模拟一半的区域,数值网格划分见图 2,网格数约为250 000,该网格系统已经进行过网格独立性验算,可以保证足够的计算精度。
热储中心温度为 180℃,当地的地温梯度为0.04℃/m,热储大约位于地表下4 000 m位置,岩石边界为定温边界。注入流体(水)的温度为70℃。初始时,热储中裂隙流体与当地岩石温度相同,注入井和生产井中都充满70℃的流体。所有与流体接触的壁面均为非滑移边界,注入井入口定质量流量,采出井出口定压力。岩石和流体的热物性参数设定为常数,如表1列示。
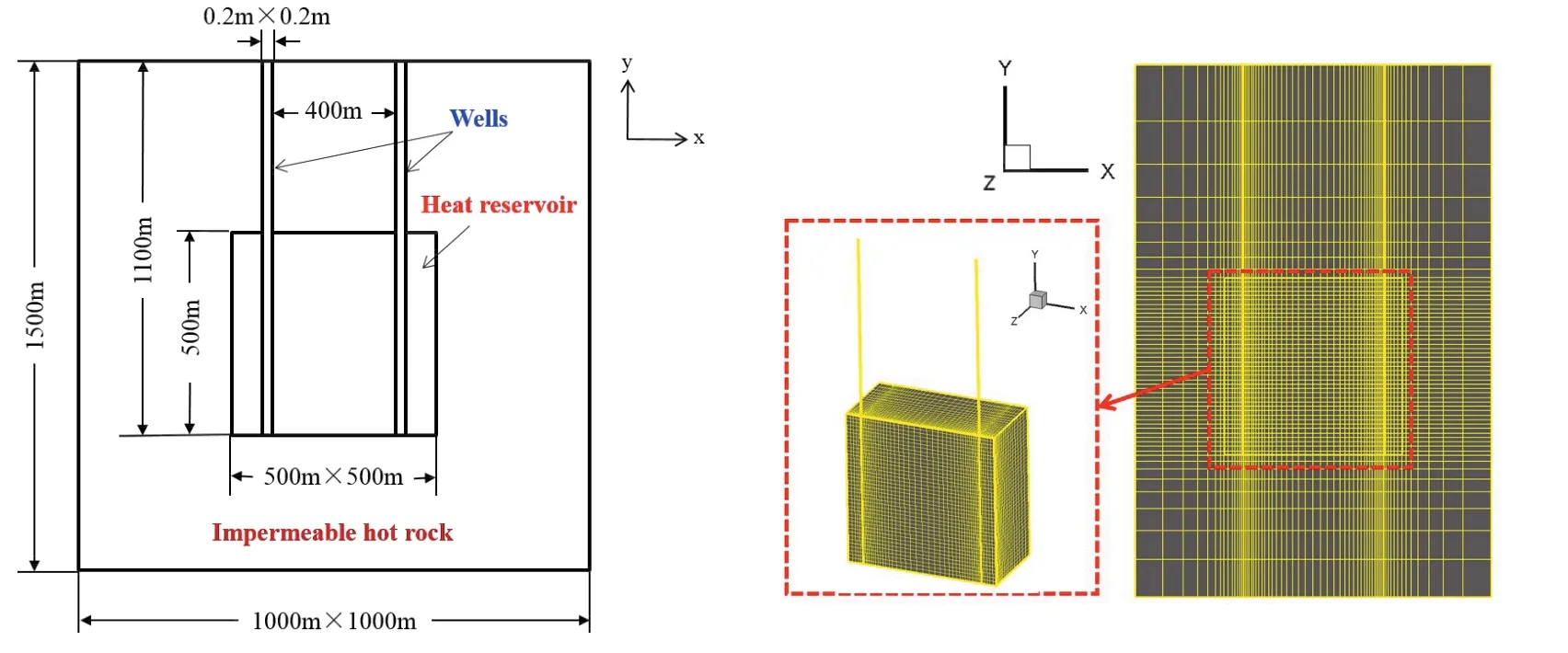
图2 双井EGS几何参数和数值网格示意Fig. 2 Geometrical dimensions and numerical system of the considered doublet EGS

表1 流体和岩体的热物性参数Table 1 Thermophysical properties of fluid and rock
2.2 热储构建
考虑三个不同孔隙度分布的分层热储,包括两个不均匀热储(HER1,HER2)和一个均匀热储(HOR)。三个热储的平均孔隙度一样,都为0.01,热储孔隙度沿深度方向的分布如图3所示。
热储不同层渗透率的确定依据Verma-Pruess模型[31]:
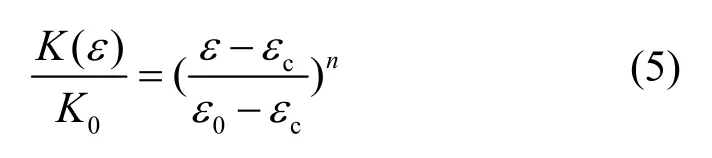
其中,εc表示临界孔隙度,εc=0.8ε0;基准孔隙度ε0和渗透率K0分别取为0.01和1 × 10-14m2;增长指数n取为3。

图3 孔隙度沿深度方向的变化Fig. 3 Porosity profile along the depth direction
3 分析与讨论
为方便讨论EGS的采热性能,我们引入整体采热率和局部采热率的概念[16]。整体采热率γ(t)(Heat extraction ratio)指在时刻t,EGS已经开采的热能与热储中可利用总能量的比值。局部采热率γ1(t)(Local heat extraction ratio)指在时刻t,热储岩石局部位置已经开采的热量与当地可利用总能量的比值。两者定义式分别为:

其中,Ts和Ts(t)分别表示岩石的初始温度和t时刻的温度,Tf,in和Tf,out分别表示注入井和生产井流体的温度,qv为流体工质的循环体积流量。
文章中判断热穿透(Thermal breakthrough)出现的标准为开采过程中生产井周围区域的局部采热率达到0.01,定义EGS使用年限为生产井出口流体温度下降10 K时EGS所经历的运行时间。
3.1 热储非均质性的影响
3.1.1 采热性能
图4显示了在定循环流量下(75 kg/s)3组不同热储EGS生产温度和采热率随时间的变化情况,并示出了当EGS到达使用年限(出口井温降为10 K)时的采热率。

图4 热储非均质性对生产井温度和采热率的影响Fig. 4 The influence of reservoir heterogeneity on production temperature and heat extraction ratio
不同热储EGS对应的曲线显示出相同的变化趋势,在采热初期,出口井流体温度会维持在某一较高采热温度,随后会随EGS的运行而逐渐降低。然而,不同热储EGS生产温度变化速度明显不同,相比于HOR EGS,HER1 EGS和HER2 EGS生产温度开始下降的时间较早,并且温度的下降也更加迅速,使后两者更早地达到使用年限,导致所开采的热总量较低。
3.1.2 渗流场和温度场
为了进一步寻找不均匀热储采热性能较差的原因,选取HOR EGS和HER1 EGS,对这两者的渗流场和温度场进行分析比较。
因为热储渗透率极低,井中的流阻相对热储内Darcy阻力可以忽略[16],流体在热储中沿深度方向的流速相对于水平方向(X,坐标系参见图2)流速可以忽略。图5示出了在75 kg/s工质流量时,HOR和 HER1热储内的 X方向流体渗流速度分布。在HER热储内,流体工质在达西阻力小的高渗透性区域形成明显的优势流动。
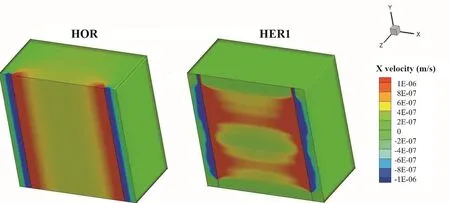
图5 定流量下(75 kg/s)HOR与HER1内的渗流场Fig. 5 Seepage flow field in HOR and HER1 (75 kg/s flow rate)
图6截取了HOR和HER1在5.357年和10.702年的热量开采情况:a~d为热储温度分布情况;e~h为热储局部采热率分布情况,其中三个等值面的局部采热率分别为0.99、0.20和0.01。
局部采热率为0.01的等值面可以近似表示热开采过程在热储中到达的前沿位置,当该等值面到达生产井时,认为该区域已经出现热穿透现象。如图6所示,HER1中的优势流动区域热开采速度明显高于其他区域。在5.357年时,HER1中的优势流动区域已经发生热穿透(图6f),导致HER1 EGS生产井温度下降(参见图4)。与之相比热开采在HOR 更均匀进行,当开采时间进行到10.702年时,HOR才出现热穿透现象(图 6g)。另一方面,出现热穿透之后,生产井附近的热储区域温度会迅速降低,导致生产井温度进一步下降,缩短了系统的使用年限。从图6h中可以看出,当开采进行到10.702年时,在HER1的优势流动区域中,局部采热率为0.99的等值面已经迫近生产井,这时生产井出口流体温降达到11.07℃,HER1 EGS已经超过了使用年限。此时,HER1热储中部分区域的热开采过程还未充分进行,导致了热储利用率较低。
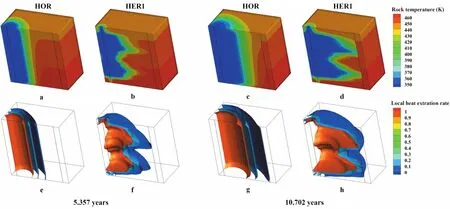
图6 HOR与HER1内岩石温度场(a~d)和当地采热率分布情况(e~h)Fig. 6 Distribution of rock temperature (a~d) and local heat extraction ratio (e~h) in two reservoirs (HOR and HER1)
3.2 定量化评估
从以上分析中可以看出,热储在竖直方向非均质性会引起系统采热性能的下降。为了定量评估热储的非均质性对系统采热性能的影响,本文从以下三个方面展开工作:(1)分析热储结构特性对采热性能的影响,归纳总结适合描述不均匀热储结构特征的统计参数;(2)比较HER1、HER2和HOR三种热储EGS在多种运行条件下的模拟结果,寻找能够关联 EGS采热性能和热储非均质性的指标因子;(3)模拟更多具有不同热储结构EGS的长期运行,根据模拟结果拟合出EGS采热性能与热储非均质性之间的函数关系。
3.2.1 热储不均匀度α
我们定义 EGS热储不均匀度α(Reservoir heterogeneity)以定量化描述热储的分层非均质性,要求该参数能够充分地体现热储非均质性对EGS采热过程的影响。从3.1.2的分析中可以看出,热储中流量分布的不均匀是引起EGS使用效率下降的关键因素。而热储中各个流动区域的流量的方差,是评价热储中流量分布不均匀程度最直观的统计参数。因此我们采用类似方差的形式,用流量系数的m阶偶数中心距定义热储不均匀度α来描述热储的非均质性。其表达式为:
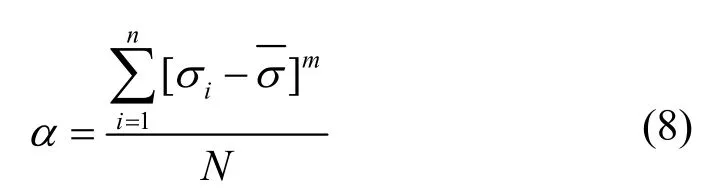
其中,N为分层热储模型的层数(本文中N=10),m为中心距的阶次(m可取值2、4、6、8等)。流量系数σi为分层热储中第i个流动区域中的流量占总流量的比例(为所有流动层流量系数的平均值),其定义式为:

上式中,q为系统的总流量,qi为第i个流动区域中的流量。
在所考虑的分层热储模型中,流量系数可以进一步由每个流动区域的渗透率表示。流体工质在井筒中因流动的粘性力产生的压降要远远小于其在热储中由达西阻力导致的压降,在热储渗透率小于10-12m-2时EGS的井筒中可近似看做定压力[16]。所以图1中的各个流动层可视为在两井之间相互“并联”,由达西定理[32]可知:


式中,Ai和A分别表示第i个流动区域在两井间的等效截面积和热储区域的等效截面积(由于考虑的模型被均分为10个流动区域,因此Ai=A/10);Ki和K分别表示第i个流动区域渗透率和热储区域的宏观渗透率;μ为流体动力粘性系数;ΔP为入口井到生产井的压降。
结合式(10)和式(11),第i个流动层的流量系数σi可直接由渗透率计算得出:
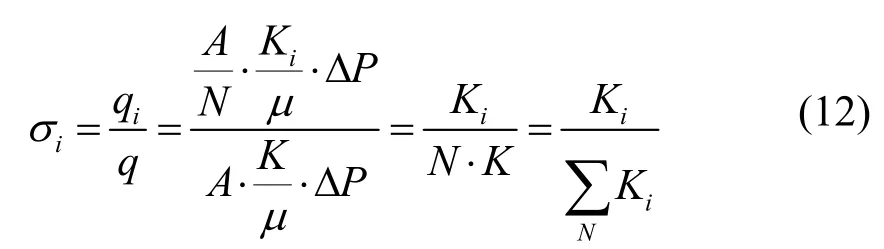
由式(8)和式(12)我们可以得到由热储各个流动层的渗透率计算得到热储的不均匀度α:
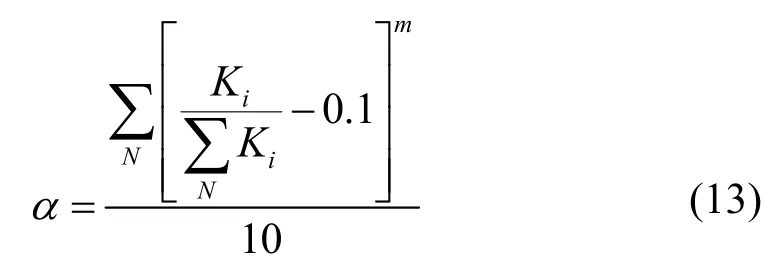
3.2.2 相对采热率η
我们的目标是建立热储的非均质性与EGS采热性能的定量关系。为了增强该结果的通用性,我们希望所采用的评价EGS采热性能的指标因子不仅能够区分热储非均质性,还要不受其他运行条件(流体流量、热储尺寸)的影响。为此我们比较了HER1、HER2和HOR三种热储EGS在多种运行条件下的模拟结果。
图7显示了三个热储(HOR、HER1、HER2)在不同流量下的采热情况。图7a显示了EGS采热率γ 随生产井流体温降δ(Production temperature decline)的变化,可以看出在相同流量下,均匀热储(HOR)的采热率都明显高于不均匀热储(HER1和HER2)。另一方面,EGS热储在热开采过程中存在热补偿现象,热储会不断地从周围岩石中吸收热量,循环流量较小时EGS热开采过程进行缓慢,使热储能够更充分地吸收周围岩石的热量,增加了EGS采热总量,使系统采热率发生改变:在热储HER1中,当流量从75 kg/s变为37.5 kg/s、生产井流体温降为10℃时的采热率从0.295变为0.341,变化率为15.6%。可以看出,EGS采热率虽然能够区分热储的非均质性,但循环流量的变化对EGS采热率也有很大的影响。
为了突出热储非均质性的影响,我们引入了相对采热率η(Relative heat extraction ratio)。其定义为在相同的运行条件下生产井流体达到相同的温降时系统的采热率γ与均匀热储采热率γ0的比值,表达式为:

如图7b中所示,采热曲线明显地分成了三组。与图7a相比,流量因素的影响几乎完全消除。同样,在热储HER1中,当流量从75 kg/s变为37.5 kg/s、温降为10 K时的相对采热率从0.666变为0.686,变化率为3.0%。热储非均质性成为影响系统相对采热率的主导性因素。

图7 EGS在不同流量下的采热率(a)和相对采热率(b)随生产井温降的变化Fig. 7 Heat extraction ration (a) and relative heat extraction ratio (b) versus production temperature decline for the EGS cases
对于不同的EGS,热储厚度、两井间距离和热储区域宽度可能会有所不同。为了验证相对采热率对这些因素敏感性,模拟了当HER1热储模型在各个方向上的尺寸发生变化时的运行情况。考虑到当热储长度缩短时,由于工质在热储中流动距离的缩短,热储热量的开采速度会相对变快。这与系统运行流量增大时的情况相似。为了避免计算结果与之重复,我们在设置热储长度缩小的算例时,以相同的比例减小了系统的运行流量。结果如图8所示。图中lx、ly、lz分别表示立方体热储在x、y、z三个方向上的边长,当立方体边长改变时热储内部尺寸也以相同比例变化。
可以看出,当热储尺寸发生变化时不均匀热储的相对采热率并无明显变化。从局部放大图中看到,热储长度lx的减小几乎不引起相对采热率的改变,说明两井距离并不会影响系统的相对采热率。热储高度ly的减小会导致相对采热率的小幅上涨,而热储宽度lz的减少会导致相对采热率的小幅下降,但变化幅度十分微弱。说明流动层厚度和热储宽度的改变都不会对EGS相对采热率产生明显影响。
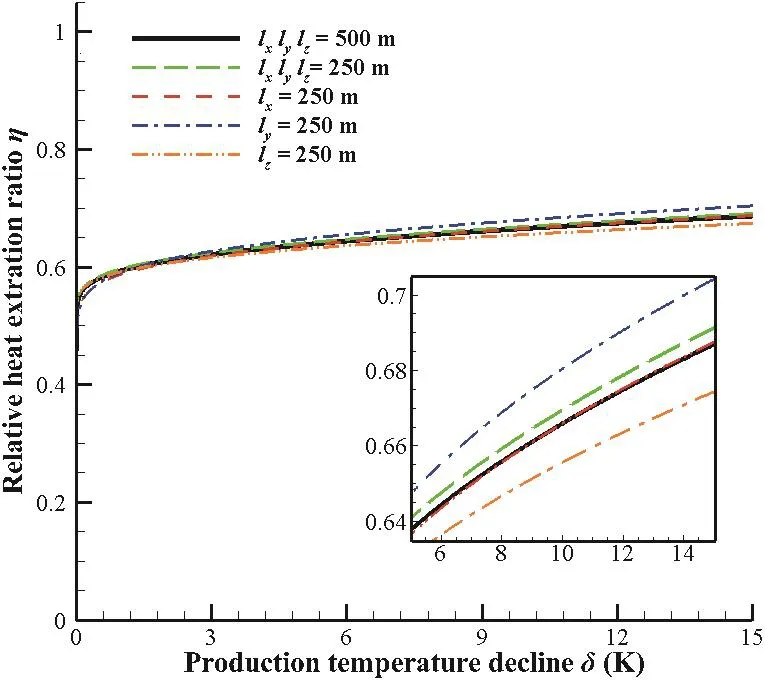
图8 不同尺寸HER1 EGS相对采热率随生产井温降的变化Fig. 8 Relative heat extraction ratio versus production temperature decline for HER1 EGSs of differing sizes
通过以上分析,我们看到相对采热率η不仅可以有效表征热储非均质性对EGS采热的影响,而且η-α关系受流体循环流量和热储尺寸的影响很小。采用相对采热率η作为描述 EGS采热性能的指示因子,可以使研究结果更具通用性。
3.2.3 η与α拟合关系
为探求普遍情形下EGS中相对采热率η和热储不均匀度α之间的关系,形成系统的、定量的研究结论。本文通过分析多个不均匀热储模拟结果,尝试总结出在一定情形下具有普适意义的关系式。为此,我们构建了30个不同的热储,每个不均匀热储都划分为10个孔隙度不同的热储层(参考HER1和HER2),而每个热储层的孔隙度都利用Matlab中高斯分布随机数生成器(Normrnd函数)随机赋值,并保证10个热储层的平均孔隙度为0.01。此外,为了对不均匀热储的不均匀程度加以区分,30个热储孔隙标准差(Standard Deviation, STD)在0.01~1 × 10-3范围内变化。模拟时循环流量统一设为75 kg/s,热储都是边长为500 m的正方体,并采用系统达到使用年限(生产井温降δ=10 K)时的相对采热率作为评价指标。
通过对模拟结果进行拟合处理,发现m=4时的热储不均匀度α与系统相对采热率η之间存在很好的关联性。如图9所示,当用热储孔隙度的标准差作为横坐标时,标准差大于0.3 × 10-3的数据点分布分散,热储孔隙度的标准差与系统的相对采热率并没有很大的关联性;当使用热储不均匀度α(m=4)作为横坐标时,数据点的离散程度明显降低,数据点可以使用一个双曲正切函数进行拟合:

该拟合结果的平均相对误差为 2.24%,最大相对误差为 7.45%(该相对误差为拟合误差与模拟结果值的比值)。
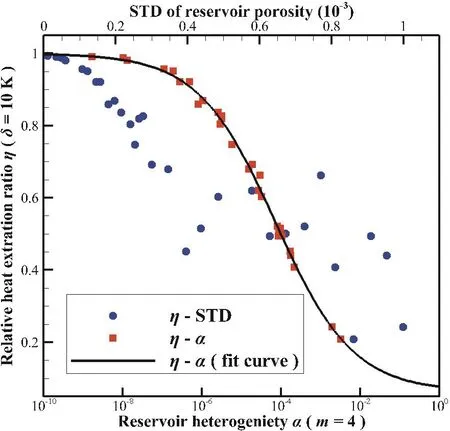
图9 30个算例的模拟结果与拟合曲线(考虑生产井温降为10 K时的相对采热率,取m=4计算热储不均匀)Fig. 9 η-αrelationship based on data from 30 simulations (ηvalues taken at 10K production temperature decline, andαvalues calculated withm=4)
从拟合结果可以看出,当热储不均匀度α的量级为 10-6时,系统的相对采热率η低于 0.9;当α进一步增大时,η出现显著下降,此时热储的非均质性对系统的采热性能造成了较大影响。
4 总 结
考虑到热储在竖直方向的非均质性,本文将不均匀热储假设为分层等效多孔介质。研究发现,分层不均匀热储中各个流动层流体流量的差别是导致系统采热性能下降的最主要原因。
在分层热储模型基础上,本文引入一种全新的热储非均质性描述和评价方法:由热储的渗透率分布情况计算出热储不均匀度α,并使用相对采热率η来表示不均匀热储采热性能的下降。
本文通过随机赋值方法构建了多个不同的热储结构,并模拟了它们各自的长期运行情况。基于这些模拟结果,发现使用各个流动层流量系数的四阶中心距α能够很好地关联热储非均质性与EGS采热性能,并给出了η和α的拟合关系式。
根据该关系式,可以直接利用不均匀热储渗透率的分布情况对具有分层热储结构的EGS采热性能进行定量预测。不均匀热储在不同的运行流量、热储尺寸下的运行情况的模拟结果显示该η与α关系式受流体流量、热储尺寸影响较小,这表明该关系式具有良好的通用性。
[1] Tester J W, Anderson B J, Batchelor A S, et al. The future of geothermal energy[R]. Massachusetts Institute of Technology, 2006.
[2] 蔺文静, 刘志明, 马峰, 等. 我国陆区干热岩资源潜力估算[J]. 地球学报, 2012, 33(5): 807-811.
[3] 汪集暘, 胡圣标, 庞忠和, 等. 中国大陆干热岩地热资源潜力评估[J]. 地热能, 2013, (3): 3-10.
[4] 许天福, 张延军, 曾昭发, 等. 增强型地热系统(干热岩)开发技术进展[J]. 科技导报, 2012, 30(32): 42-45.
[5] 郭剑, 陈继良, 曹文炅, 等. 增强型地热系统研究综述[J]. 电力建设, 35(4): 10-24.
[6] Breede K, Dzebisashvili K, Liu X, et al. A systematic review of enhanced (or engineered) geothermal systems: past, present and future[J]. Geothermal Energy, 2013, 1(1): 4.
[7] McClure M W. Fracture stimulation in enhanced geothermal systems[D]. California: Stanford University, 2009.
[8] Dezayes C, Genter A, Hooijkaas G R. Deep-seated geology and fracture system of the EGS Soultz reservoir (France) based on recent 5km depth boreholes[C]// Proceedings World Geothermal Congress 2005, Antalya, Turkey, 24-29 April, 2005.
[9] Genter A, Evans K, Cuenot N, et al. Contribution of the exploration of deep crystalline fractured reservoir of Soultz to the knowledge of enhanced geothermal systems (EGS)[J]. Comptes Rendus Geoscience, 2010, 342(7): 502-516.
[10] Jung A, Fenwick D H, Caers J. Training image-based scenario modeling of fractured reservoirs for flow uncertainty quantification[J]. Computational Geosciences, 2013, 17(6): 1015-1031.
[11] Berkowitz B. Characterizing flow and transport in fractured geological media: A review[J]. Advances in water resources, 2002, 25(8): 861-884.
[12] Dershowitz W S, La Pointe P R, Doe T W. Advances in discrete fracture network modeling[C]//Proceedings of the US EPA/NGWA Fractured Rock Conference, Portland. 2004: 882-894.
[13] Jiang F, Luo L, Chen J. A novel three-dimensional transient model for subsurface heat exchange in enhanced geothermal systems[J]. International Communications in Heat and Mass Transfer, 2013, 41: 57-62.
[14] 陈继良, 蒋方明. 增强型地热系统热开采性能的数值模拟分析[J]. 可再生能源, 2013, 31(012): 111-117.
[15] 陈继良, 罗良, 蒋方明. 热储周围岩石热补偿对增强型地热系统采热过程的影响[J]. 计算物理, 2013, 30(6): 862-870.
[16] 陈继良, 蒋方明, 罗良. 增强型地热系统地下渗流场的模拟分析[J]. 计算物理, 2013, 30(6): 871-878.
[17] Arbogast T, Douglas, Jr J, Hornung U. Derivation of the double porosity model of single phase flow via homogenization theory[J]. SIAM Journal on Mathematical Analysis, 1990, 21(4): 823-836.
[18] Gelet R, Loret B, Khalili N. A thermo-hydro-mechanical coupled model in local thermal non-equilibrium for fractured HDR reservoir with double porosity[J]. Journal of Geophysical Research: Solid Earth (1978-2012), 2012, 117(B7): B07205-B07228.
[19] Pruess K. The TOUGH codes-A family of simulation tools for multiphase flow and transport processes in permeable media[J]. Vadose Zone Journal, 2004, 3(3): 738-746.
[20] Xu T, Spycher N, Sonnenthal E, et al. TOUGHREACT Version 2.0: A simulator for subsurface reactive transport under non-isothermal multiphase flow conditions[J]. Computers & Geosciences, 2011, 37(6): 763-774.
[21] Kalinina E, McKenna S A, Hadgu T, et al. Analysis of the effects of heterogeneity on heat extraction in an EGS represented with the continuum fracture model[C]// Proceedings, 37th Workshop on Geothermal Res. Eng., Stanford Univ., Stanford, CA, Jan. 2012.
[22] Shaik A R, Rahman S S, Tran N H, et al. Numerical simulation of Fluid-Rock coupling heat transfer in naturally fractured geothermal system[J]. Applied Thermal Engineering, 2011, 31(10): 1600-1606.
[23] Vogt C, Marquart G, Kosack C, et al. Estimating the permeability distribution and its uncertainty at the EGS demonstration reservoir Soultz-sous-Forêts using the ensemble Kalman filter[J]. Water Resources Research, 2012, 48(8): W08517-W08531.
[24] Vogt C, Kosack C, Marquart G. Stochastic inversion of the tracer experiment of the enhanced geothermal system demonstration reservoir in Soultz-sous-Forêts-Revealing pathways and estimating permeability distribution[J]. Geothermics, 2012, 42: 1-12.
[25] Fourar M. Characterization of heterogeneities at the core-scale using the equivalent stratified porous medium approach[C]//SCA International Symposium. Trondheim, Norway. 2006.
[26] Radilla G, Sausse J, Sanjuan B, et al. Interpreting tracer tests in the enhanced geothermal system (EGS) of Soultz-sous-Forêts using the equivalent stratified medium approach[J]. Geothermics, 2012, 44: 43-51.
[27] Blöcher M G, Zimmermann G, Moeck I, et al. 3D numerical modeling of hydrothermal processes during the lifetime of a deep geothermal reservoir[J]. Geofluids, 2010, 10(3): 406-421.
[28] Luo F, Xu R N, Jiang P X. Numerical investigation of fluid flow and heat transfer in a doublet enhanced geothermal system with CO2as the working fluid (CO2-EGS)[J]. Energy, 2014, 64: 307-322.
[29] Luo F, Xu R N, Jiang P X. Numerical investigation of the influence of vertical permeability heterogeneity in stratified formation and of injection/production well perforation placement on CO2geological storage with enhanced CH4recovery[J]. Applied Energy, 2013, 102: 1314-1323.
[30] He L W, Jin Z H. A local thermal nonequilibrium poroelastic theory for fluid saturated porous media[J]. Journal of Thermal Stresses, 2010, 33(8): 799-813.
[31] Lai K H, Chen J S, Liu C W, et al. Effect of permeability–porosity functions on simulated morphological evolution of a chemical dissolution front[J]. Hydrological Processes, 2014, 28(1): 16-24.
[32] 孔祥言. 高等渗流力学[M]. 合肥: 中国科学技术大学出版社, 1999. 30-37.
Numerical Study of EGS Heat Extraction from Stratified Heat Reservoirs
HUANG Wen-bo, CHEN Ji-liang, JIANG Fang-ming
(Laboratory of Advanced Energy System, CAS Key Laboratory of Renewable Energy, Guangzhou Institute of Energy Conversion, Chinese Academy of Sciences, Guangzhou 510640, China)
Strong heterogeneity exists in enhanced geothermal systems (EGS) artificial heat reservoir due to factors such as different rock formations, the pre-existence of natural fractures and the uncertainty of stimulation process. Exploring the influence of reservoir heterogeneity on EGS heat extraction is of great importance for predicting and comprehensively evaluating the performance of EGS. In this paper, we take the reservoir as an equivalent stratified porous medium and employ the previously self-developed numerical model to conduct a series of simulations of the long-term heat extraction process of EGSs with different reservoir porosity distributions. Results indicate that the heat extraction performance is significantly affected by the reservoir heterogeneity. To facilitate the analysis and evaluation, we derive a formula to quantitatively describe the heterogeneity of the reservoir based on a detailed analysis to the effects of the fluid seepage flow field on the heat extraction performance. Further, we obtain a quantitative relationship of EGS heat extraction performance versus reservoir heterogeneity by fitting the calculated results from 30 cases, in which the stratified reservoirs are randomly assigned with differing porosity distributions.
enhanced geothermal systems (EGS); numerical simulation; equivalent stratified porous medium; heterogeneity
TK529;P314
A
10.3969/j.issn.2095-560X.2014.04.009
2095-560X(2014)04-0295-10
黄文博(1990-),男,硕士研究生,主要从事增强型地热系统地下物理过程的数值模拟研究。
2014-05-23
2014-07-09
国家高技术发展863计划项目(2012AA052802);中国科学院“百人计划”项目
† 通信作者:蒋方明,E-mail:jiangfm@ms.giec.ac.cn
蒋方明(1973-),男,博士,研究员,博士生导师,中国科学院广州能源研究所先进能源系统实验室主任。2001年博士毕业后曾先后工作于德国的 IMM 公司、葡萄牙的阿维诺(Aveiro)大学、美国的宾州州立大学,2011年4月获中国科学院“百人计划”引进海外杰出人才择优支持。目前主要从事电化学能量/动力系统、增强型地热系统、微热流体系统、以及高效节能技术/产品等研发工作。
