XK2423 数控铣床立柱的有限元分析与拓扑优化*
2014-06-29刘甚宏关英俊张力锋毕海峰
刘甚宏,关英俊,张力锋,李 想,毕海峰
(1.长春工业大学 机电工程学院,长春 130012;2.长春数控机床有限公司,长春 130033)
0 引言
XK2423 数控龙门铣床是由当代机械、电气、液压等新技术设计而成的机床,该机床适用范围较大、功能广泛,能实现大直径、大平面的切削,具有较强的铣削、镗孔、钻孔的功能,属于高精度、高性能、高效率的关键重大设备。立柱作为龙门铣床的关键受力部件,它承载了横梁、滑枕、主轴箱等关键部件的重力,其强度和刚度的大小会对龙门铣床的加工精度和使用寿命产生直接的影响,因此对立柱部件进行分析设计的过程中,要保证它具有足够高的动静态特性。由于该机床的技术水平及标准都较高,传统的经验及类比设计方法已远远满足不了该机床的高精度技术指标要求[1]。鉴于该机床按传统经验进行研制的技术风险及成本较高,我们引入了有限元分析技术和更加精细准确的形状优化、尺寸优化、拓扑优化等结构优化设计方法,使设计的产品为今后的设计工作提供更加有效的参考[2]。本文利用有限元分析软件HyperWorks 对立柱进行了动静态刚度分析,并在此基础上采用拓扑优化方法对立柱进行结构优化设计,对立柱的结构及尺寸参数进行了重新布置,并对新的立柱结构进行了有限元分析验证,所做的研究对后续工作具有一定的指导意义。
1 拓扑优化理论
1.1 密度法拓扑优化
从20 世纪末期以来,产生了许多拓扑表达形式和拓扑材料插值模型方法如均匀化方法、密度法、渐进结构优化法、拓扑函数描述方法以及水平集方法等,其中以均匀化法和密度法最具代表性。本文就是采用了基于密度法,在SIMP 插值模型的基础上对立柱结构进行拓扑优化计算的连续体拓扑优化方法。
密度法结构拓扑优化以连续变量的密度函数形式表达单元相对密度与材料弹性模量之间的对应关系。这种方法基于各向同性材料,不需引用微结构和附加的均匀化过程,以有限元模型设计空间的每个单元的单元密度作为设计变量,该“单元密度”同结构的材料参数有关(单元密度与材料弹性模量E 之间具有某种函数关系),在0~1 之间连续取值,优化求解后单元密度为1(或靠近1)表示该单元位置处的材料很重要,需要保留;单元密度为0(或靠近0)表示该单元处的材料不重要,可以去除,从而达到材料的高效利用,实现轻量化设计[3]。密度法程序设计简单,计算效率高,是从均匀化方法发展而来的一种方法。
1.2 基于OptiStruct 的结构优化数学模型及优化流程
OptiStruct 是HyperWorks 内含的功能强大的有限元分析和结构优化设计软件,覆盖复合材料和金属、静态和动态、线性和非线性优化应用领域,支持全面的优化类型,比如形状优化、尺寸优化以及拓扑优化等。OptiStruct 的优化设计包括三个要素,即目标函数、约束条件和设计变量。目标函数是要求达到的最优的设计性能;设计变量是发生变化从而提高结构性能的一组参数;约束条件是对设计变量的限制,是对设计变量和其他性能的要求。
OptiStruct 结构优化的数学模型为:

OptiStruct 采用数学规划的方法,通过求解灵敏度构造近似的显式模型,采用小步长迭代的方法寻找最优解,是一种高效稳健的优化方法,其内部的优化流程如图1 所示[4]。
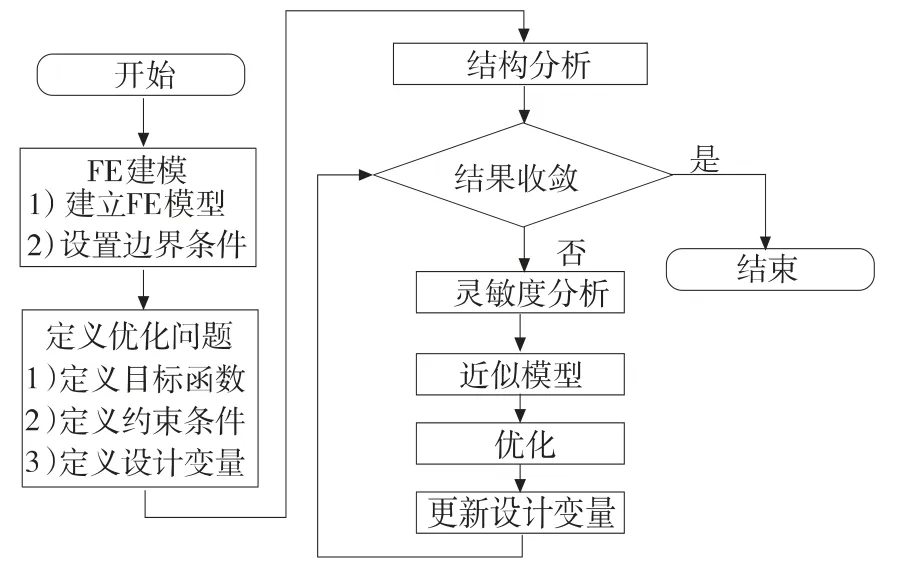
图1 OptiStruct 内部优化流程
2 XK2423 立柱的有限元分析
2.1 建立立柱的有限元模型
数控龙门铣床的立柱是带圆孔的筋板式结构,各连接处有过渡圆角,结构比较复杂,所以在实体建模之前,应先在三维软件SolidWorks 中对模型进行必要的简化,比如去除对计算结果影响较小的部分局部特征如倒角、圆角、螺钉孔、凸台等。然后导入HyperMesh软件进行网格划分,设置材料、属性,材料为灰铸铁HT300,假设材料为各向同性、介质均匀,其弹性模量E=130GPa、泊松比μ =0.27、密度ρ =7300kg/m3。
机床主轴的最大切削载荷对立柱的最大载荷产生主要的影响,当主轴处于横梁的中间位置时立柱端面受到的载荷最大,所以我们只有分析此极限工况下立柱的最大变形及应力分布情况,才能为立柱的结构优化提供有效的参考[5]。由机床各零部件的联接关系可知,立柱的底面与地面直接接触,底部一侧与床身用螺栓连接在一起[6],所以对立柱进行分析时应对这两部分施加全约束。经过约束和加载后的立柱有限元模型如图2 所示。

图2 立柱有限元模型
2.3 立柱的有限元分析
通过模态分析得到立柱第一阶固有频率为83.5Hz,振型为立柱的前后仰合,第二阶固有频率为159.5Hz,振型为立柱Y向扭转变形。低阶固有频率大于切削加工时的激振频率,不会发生共振,满足设计指标要求。由静力分析得到的立柱变形和应力分布情况分别如图3、图4 所示。

图3 立柱的变形图

图4 立柱的应力图
由图3 可知立柱的变形主要集中在上半部分,最大变形为40.95μm,变形很小,不会在极限工况下发生破坏,满足设计指标要求。由图4 立柱的应力分布图可知,立柱所受的最大应力为3.95MPa,出现在立柱一侧应力较为集中的部位。由于立柱的材料为HT300,其抗拉强度为300MPa 远大于立柱所受的最大应力值,所以从应力的角度分析,立柱有很大的抗破坏潜力,设计过于保守,造成材料浪费,可对其进行在保证动静态刚度不减小的情况下实现轻量化设计,使材料的分布更加合理[7]。
3 立柱的结构优化设计及分析
3.1 立柱的拓扑优化
在进行拓扑优化时,可以使用多个从动静态有限元分析中得到的结构响应定义约束函数和目标函数。本文主要利用有限元分析软件HyperWorks 中的优化模块Optistruct 对XK2423 数控铣床中的关键部件立柱进行拓扑优化设计,拓扑优化过程中的响应函数有体积分数、应变能、静态位移,定义体积分数和静态位移为约束函数,应变能为目标函数。
Optistruct 利用HyperMesh 进行拓扑优化问题的前处理和定义,在HyperMesh 中完成立柱的有限元建模后,利用优化面板定义设计变量、约束函数、目标函数及优化参数;然后利用Optistruct 模块进行拓扑优化计算;最后利用后处理模块HyperView 对拓扑优化后的结构进行后处理[8]。
考虑到立柱和其它零部件的配合问题,把立柱的上面和底面定义为非设计区,定义位移(displacement)响应(response)不超过40.95 μm,定义要保留的体积分数的上限为40 ﹪,收敛误差为0.0001,经过46 次迭代后完成立柱的拓扑分析,设计区域的优化密度云图和目标函数迭代收敛曲线如图5、图6 所示
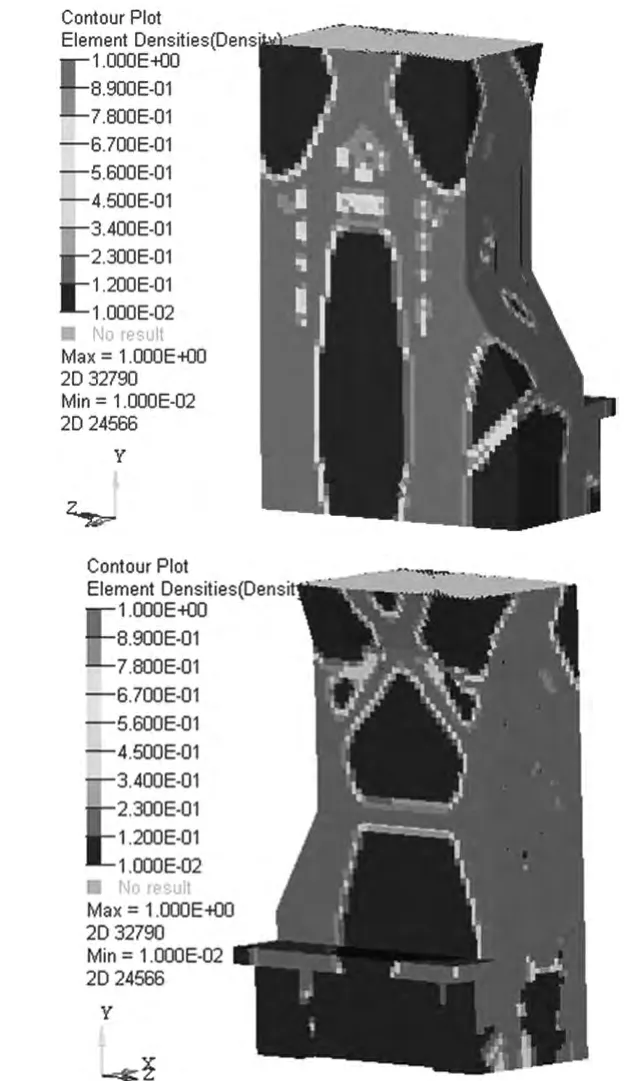
图5 密度云图
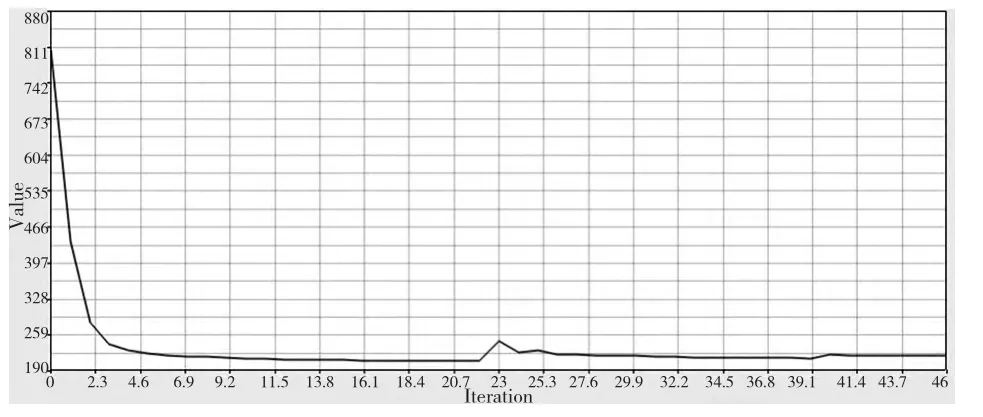
图6 目标函数迭代收敛曲线
3.2 模型优化改进
拓扑优化结果大部分是不规则的空间结构,因此要对拓扑优化结果进行抽象和简化[9]。由立柱的拓扑优化结果可知图中的红色区域为需要保留并起主要作用的部分,而其他地方需要改进。由拓扑云图可知,对立柱前后面筋板形状需要进行改进,两侧为红色区域,可以保留初始设计,改进前后立柱局部剖视图如图7所示。
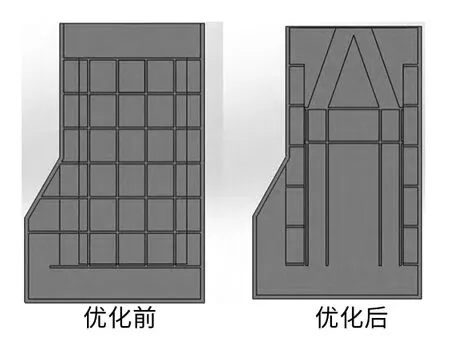
图7 立柱局部剖视图
3.3 优化前后对比分析
提出优化方案后,要对优化前后的结果进行分析比较。评判一个优化方案的优劣需要遵循的基本原则有:每个设计并不一定要达到理论上的最优解,但要确保每次设计相比原设计是改进的设计;另外要综合评价技术与经济度,对每一个设计方案的评价,并不是单纯的考虑结构设计,也要考虑加工工艺,在遵循技术指标的同时尽量提升经济指标。本着这两点原则,对此次优化方案进行分析时主要从立柱优化前后质量的变化度以及动静态刚度的改善等方面着手[10]。
对拓扑优化后的立柱进行静、动态有限元分析。优化后立柱的位移和应力云图如图8 所示。从分析结果(表1)看,在施加相同载荷和约束的情况下优化后的立柱具有更高的共振频率、更小的最大变形,而且质量也有所降低。综合立柱性能和经济度,表明此优化方案在加工工艺和经济允许的情况下,显著的提高了立柱的静、动态特性。量有所降低,节约了材料,获得了经济效益。同时,立柱的静动态刚度特性也得到了显著的提高,为立柱的设计提供了参考。

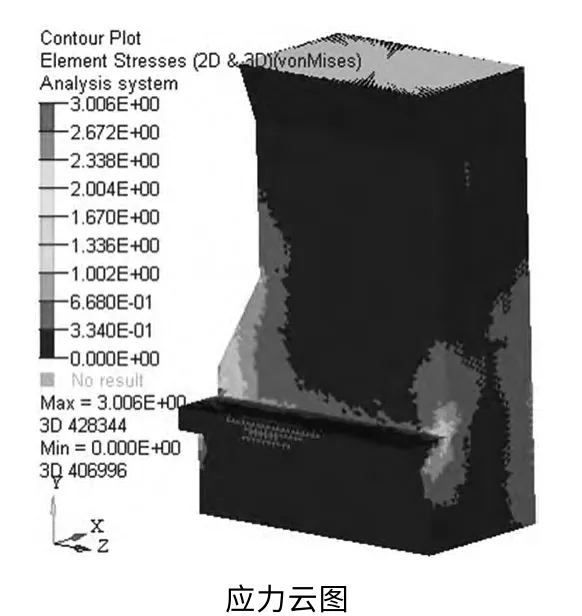
图8 位移、应力云图

表1 立柱优化前后分析结果对比
4 结论
在对XK2423 数控铣床立柱进行有限元动静态分析的基础上,使用拓扑优化分析,找出了立柱结构的最佳材料分布形式。基于此分析结果,结合生产及工艺的实际情况,获得了立柱的优化设计。结果表明,在保证立柱使用性能的前提下,优化后的结构更加合理,质
[1]黄伟,欧长松,陆海漫,等.龙门机床立柱结构的有限元分析及拓扑优化[J].机械科学与技术,2012,31(1):118-121.
[2]周克民,李俊峰,李霞.结构拓扑优化研究方法综述[J].力学进展,2005,35(1):69 -76.
[3]李磊,洪荣晶,张建润,等.立式铣削加工中心立柱结构拓扑优化设计[J].机床与液压,2007,35(4):16 -18.
[4]洪清泉,赵康. OptiStruct ﹠ HyperStudy 理论基础与工程应用[M].北京:机械工业出版社.2013.
[5]刘战强,万熠,艾兴.高速铣削中切削力的研究[J].中国机械工程,2003,14(9):734 -737.
[6]米洁,郑孝,陈祥臻.数控立式磨床关键部件的结构设计及动态特性分析[J].机床与液压,2013,41(17):24 -27.
[7]韩滔.高速立式加工中心关键部件结构优化[D]. 大连:大连理工大学,2010.
[8]蒋素清,杜娟.高速立式加工中心立柱结构拓扑优化设计[J].计算机应用技术,2007(8):36 -38.
[9]蒋素清.精通拓扑优化在XH786A 机床立柱结构优化中的应用[J].机械设计与制造,2008(9):195 -196.
[10]杨彩芳,殷国富,苏龙.龙门加工中心立柱性能分析与拓扑优化设计[J].组合机床与自动化加工技术,2013(2):50 -53.
