基于区间层次分析法的城市天然气供应系统风险评价

同济大学 刘东京 周伟国 潘新新

基于区间层次分析法的城市天然气供应系统风险评价

同济大学 刘东京 周伟国 潘新新

用区间数描述城市天然气供应系统的复杂性、模糊性及不确定性，对评价体系各层因素进行群体判断，得出群决策判断区间上三角矩阵；以区间层次分析法确定评价体系各底层因素的权重值，通过权重的分配率计算出各底层因素的最大评分区间，并得到系统的相对风险区间。再以城市天然气输配系统为例，构建了区间指数风险评价模型，通过系统灵敏度分析建立风险决策系统。

燃气 风险评价 层次分析法 区间指数 群决策

0 前言

关于城市天然气供应系统的风险评价方法，国内外已进行了较多研究，提出了故障树法、KENT评分法等风险评价技术，并将各种方法进行组合运用，形成了很多新的评估方法，如模糊层次分析法、模糊综合评价法等。管道风险指数法是各种风险评价技术的综合，部分隶属于主观风险评价方法类。由于传统评价方法如指数评分法、故障树法等，无法全面合理地表达系统的复杂性以及不确定性，本文在管道风险指数法的基础上提出了区间指数分析法，并采用这种方法对城市燃气输配系统进行不确定性风险管理。

1 群决策判断区间

在进行系统评判时，由于系统的模糊性以及不确定性，评价结果很难用精确的数值进行表示，如果专家给出一个评判区间，则可以很好地表达系统评价的客观性。评判区间可以用区间数来表达，记为，该区间表示不确定性因素导致评价对象的可能判断范围，当时，评价结果为唯一值。

假设m位专家对某一评价对象分别做出判断，判断结果x={xi}={x1,x2,···xm}，xi=[xi-,xi+]，i=1,2,···m。

建立区间数判断矩阵

设评价结果的目标权重向量W1={wi1}，i=1,2,···m，则区间判断矩阵目标权重的计算公式可用矩阵形式(式(2)、(3))表示：

求解可得专家意见的目标权重向量：

综合各专家意见的过程中必须反映各专家评判水平的差异，因此在计算系统评价综合权重的过程中需要探讨各专家的评判水平，即专家权重，记为wi2。专家权重向量表示为W2={wi2}，i=1,2,···m，。专家权重可通过对专家的职称、本专业工龄、学历、年龄等属性进行综合评分并归一化处理求得。

区间判断矩阵的综合权重向量为W={wi}，i=1,2,···m，wi由下式计算得到：

群决策做出的判断p可由下式计算得到：

2 层次分析法确定指标权重

层次分析法在确定系统各层因素权重的过程中采用两两比较的方法。设P=(pij)m×m为上三角区间数判断矩阵，pij表示评判者认为方案Pi、Pj相对重要性程度存在的范围，pij取值范围在1/9和9之间，则区间层次分析法的区间数权重可由下式计算得到：

3 区间指数评价法

根据城市天然气供应系统的风险因素，先通过聚类分法确定评价系统的风险指标（评价对象），评价对象的层次可以根据实际情况调整，层数越多，操作越复杂，经济性越差，一般以2~3层为宜。以3层为例，首先对系统各层因素进行群体判断，求出群决策判断区间，然后由层次分析法计算评价系统各底层(第3层)因素的权重值：

对于燃气供应系统的输配子系统来说，其风险指数、燃气危害、泄漏状况、环境影响的各底层子因素最大评分值分别表示为、推荐值分别为400、7、6、4。

G、L、V分别表示燃气危害评分、泄漏状况评分以及环境影响评分。

燃气种类不同，相对风险区间也不相同。城市高压天然气输配系统的运行阶段，根据推荐值计算可知，相对风险区间为[0，330]；设计阶段风险评价，由于不考虑施工运行缺陷的影响，相对风险区间为[22，330]。相对风险值越大，系统越安全，所以设计阶段的相对风险最小值要大于运行阶段，即设计阶段的安全可靠性比运行阶段要高。

为增强风险评价结果的可比性，建议将风险分值统一在[0，100]之间：

同理可得城市天然气供应系统其他子系统的相对风险值。假设风险有n 个等级风险等级Rank属于第i级，如果，则风险等级可由下式计算判断：

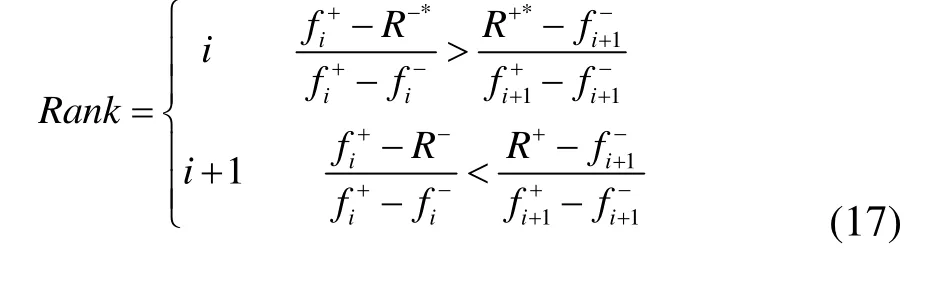
4 系统灵敏度分析

系统灵敏度主要考察系统各底层评价指标的评分变化对城市燃气输配系统的相对风险贡献度，即反映了风险可变因素在现有基础上采取更安全的措施后，评价对象安全性提高的程度。对风险可变因素各指标在现有分值的基础上，通过实施相应的有效风险缓解措施后，发生的评分变化，称之为评分增益

则灵敏度βijk可由下式计算得到：

灵敏度最高的风险可变因素必须优先进行风险管理，及时有效地执行风险管理措施，缓解风险的发生，最大程度降低系统存在的风险。

5 实例分析

以运行阶段的上海浦西天然气供应系统中燃气输配子系统为例，建立风险指标评价体系，如图1所示。图中列出系统1层因素(第三方损坏等)及部分2层风险因素(如覆盖层)，3层风险因素略。

图1 城市天然气输配系统风险评价体系

城市天然气输配系统的风险因素很多，构成指标体系也比较庞大，各项指标共邀请3位专家(均为高级工程师，工龄20年以上，专家水平很高，α=0.9)进行群决策系统评价，得出上三角区间数判断矩阵。由式(6)~(8)进行群判断，以式(9)~(10)计算指标权重，本文给出第三方损坏下一级指标(覆盖层)的权重及评分结果(表1、2)，其他各级指标在此就不一一描述。覆盖层的子因素包括：覆盖层性质、最小埋深、最大跨距、管沟情况、地形情况、管道转弯情况。

表1 群判断区间建立层次分析上三角矩阵

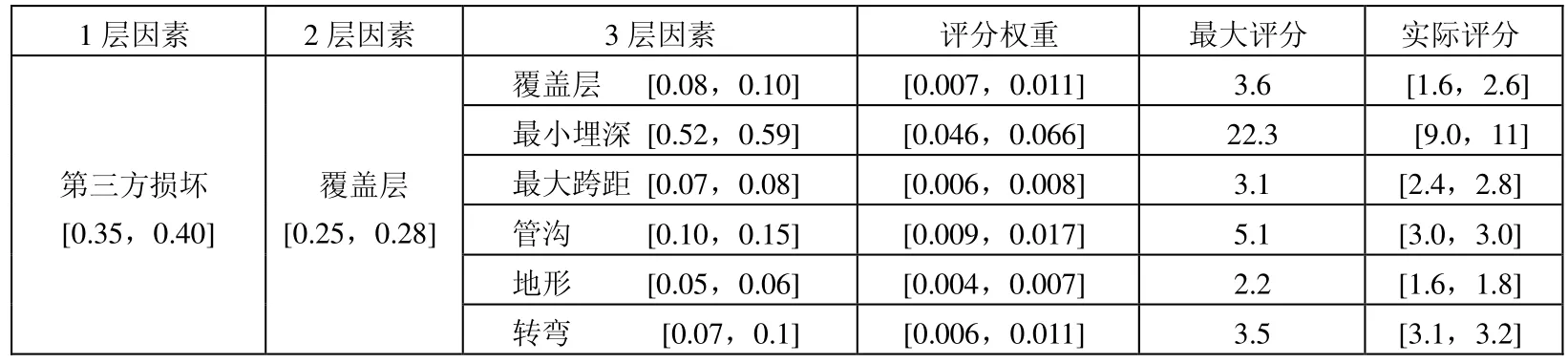
表2 覆盖层权重及评分

假设燃气输配系统风险等级为：

对上海浦西天然气输配系统的运行现状进行风险分析(表3)，由式(13)~(17)计算得出系统的相对风险为[34.3，42.0]，并通过风险等级确定系统的风险程度属于中等风险；以式(18)~(19)计算系统各因素的灵敏度，其中建筑活动的灵敏度最大，需要及时地实施相应的风险管理措施“消除违章建筑活动，制定合乎规范的建设活动，加强法制宣传教育活动”，以提高系统的安全可靠度。

表3 上海浦西天然气输配系统风险评价及决策管理

6 结语

提出了区间指数评价法，利用区间数学理论，对传统的风险评价方法进行了修正和改进。该法可以解决故障树分析法时效差的问题，并能充分考虑评价过程中的复杂性、模糊性以及不确定性，减少了评价中的人为因素，保证了评价结果的客观性。区间指数评价法适用于设计阶段、新建成阶段以及运行初期的城市天然气供应系统，即事故发生概率未知，依赖于专家判断的风险评价系统。对于在专家评价的同时，存在部分可靠的系统风险因素历史数据，或者详尽数据的情况，如已运行一段时间的城市天然气供应系统，则最好结合实际情况充分考虑数据信息与专家评价的综合影响。

Risk Assessment for Urban Natural Gas Supply System Based on I AHP

Tongji University Liu Dongjing Zhou Weiguo Pan Xinxin

Interval mathematics was used to describe the complexity, fuzziness and uncertainty of city natural gas supply system. Judgment interval upper triangular matrix based on group decision was obtained by the group judgment of each system factor whose weight value was determined by AHP (Analytic Hierarchy Process). The maximum grading intervals of each lower layer factor were computed by the appointment ratio of weight, and then the system relative risk intervals can be ensured. An interval index risk assessment model based on city natural gas transmission and distribution system was presented, the risk decision system was developed by sensitivity analysis.

gas, supply system, risk assessment, interval index, group decision