基于SPSS的沉降观测数据异常值探测与回归分析

陈文浩

(汕头市测绘研究院,广东汕头 515041)

基于SPSS的沉降观测数据异常值探测与回归分析

陈文浩∗

(汕头市测绘研究院,广东汕头 515041)

沉降观测数据受各种因素影响,观测数据的处理极其重要,本文提出利用SPSS软件对建筑物沉降观测数据进行异常值探测并进行科学取舍的思路和方法,并经过样本测试,分析比较对实测数据的回归分析法中几种曲线拟合法在预测沉降点变化中的各自的有效性和精确性。

SPSS;建筑物;沉降;观测;异常值;探测;回归分析

1 引 言

随着社会的不断进步与发展、先进科学技术与新型材料在建筑领域中的广泛应用,高层与超高层建(构)筑物的出现越来越多,为保证高层建筑物本身的正常使用寿命与安全性以及考虑对周边建筑群体带来的复杂变形影响,必须从施工到竣工直至沉降稳定阶段进行周期性的沉降观测,研究其沉降原因和规律,为建筑物的设计、施工、运营维护及科学研究提供可靠资料,及时反馈信息,预防不均匀沉降和裂缝的出现。

沉降观测中对观测数据的处理极其重要,但是观测数据受各种复杂因素的影响,存在各种误差甚至粗差。通常的做法是在沉降观测前采取各种措施预先防止各种系统误差和偶然误差的产生,通过内外业数据检查剔除粗差后再对沉降观测数据进行平差计算得到当期沉降数据,最后通过对多期观测数据的分析对建筑物的稳定性做出相应的评价和预测[1]。

本文以某新建高层建筑物的沉降量曲线出现的异常抖动现象为研究对象,使用SPSS统计分析软件,对数据进行异常值探测,排除异常的数据,从而达到优化计算数据并更好地体现出沉降规律的目的,最后通过回归分析进行稳定性的预测,以指导后期施工和设备安装。

2 沉降观测数据异常值探测和检验

在静态沉降观测中,几乎所有的新建建筑物的沉降总是一个缓慢沉降并趋于稳定的过程,各沉降点的沉降速度均匀且趋于平坦,如图1所示。

但是通过观察沉降点的沉降量曲线,会发现这些曲线并不是平缓的,各期之间的沉降差也不是均匀的,沉降量曲线在某几个周期会出现异常抖动的情况,如图2所示。

图1 建筑物X2号沉降点最后100 d沉降速度线

图2 建筑物X2号沉降点沉降过程线

通过现场荷载试验[2]的结论可知当荷载小于其临界荷载时,p-s之间呈直线关系,即可排除荷载对沉降量异常的影响;通过外业检查,排除了工作基点和监测点被破坏的情况。下面通过统计学分析,对这些由于偶然误差以及外界条件的影响而造成异常的数据进行检验,科学地对数据进行取舍。

2.1 数据异常值探测

数据曲线拟合及分析的传统方法是采用最小二乘法和坐标纸作图法,这种手工做法计算量大,精度不高,数据的计算机处理已经成为趋势。目前常见的方法是使用自编程序或Excel、Grapher等软件。自编软件往往功能单一,可视化功能差;Excel软件功能虽然较强,但对数据的处理过程中针对性不强,数据分析能力弱。而SPSS数据分析软件适合于中小型数据库的处理、分析和可视化表达,应用比较广泛。

(1)SPSS探索分析过程

SPSS的探索性分析(Explore)过程,适用于对数值型的变量(连续型或比率型)进行分析,能够生成关于所有个案、或不同分组个案的综合统计量及图形,并进行数据筛选工作,还可以进行假设检验。此过程对数据的分布没有特定限制。以该新建建筑物X2号点的沉降观测数据为例,通过探索性分析对这些数据加以详细描述,并进行数据的筛选。

(2)数据描述

该沉降点于2009年11月25日开始首次观测,于2010年10月14日结束观测,共观测38期,观测数据如表1所示。

表1 X2沉降点沉降观测数据

(3)异常值探测结果

①不考虑日期间隔的影响

选取期沉降量为因变量进行探测,描述性输出结果如表2所示,直方图如图3所示,箱图如图4所示。

表2 描述性输出

由图4可知,第2期以及第8期数据存在值偏低的异常,第7期以及第9期数据存在值偏高的异常。

图3 直方图

图4 箱图

②考虑时间间隔的影响

使用期沉降量作为因变量,同时选取时间间隔(天为单位)作为因子,考察在相同时间间隔下的数据异常。正态性检验结果如表3所示,其中时间间隔为7 d的直方图如图5所示,散点图如图6所示,箱图如图7所示。

表3 正态性检验

图5 直方图(时间间隔7 d)

图6 趋降标准散点图(时间间隔7 d)

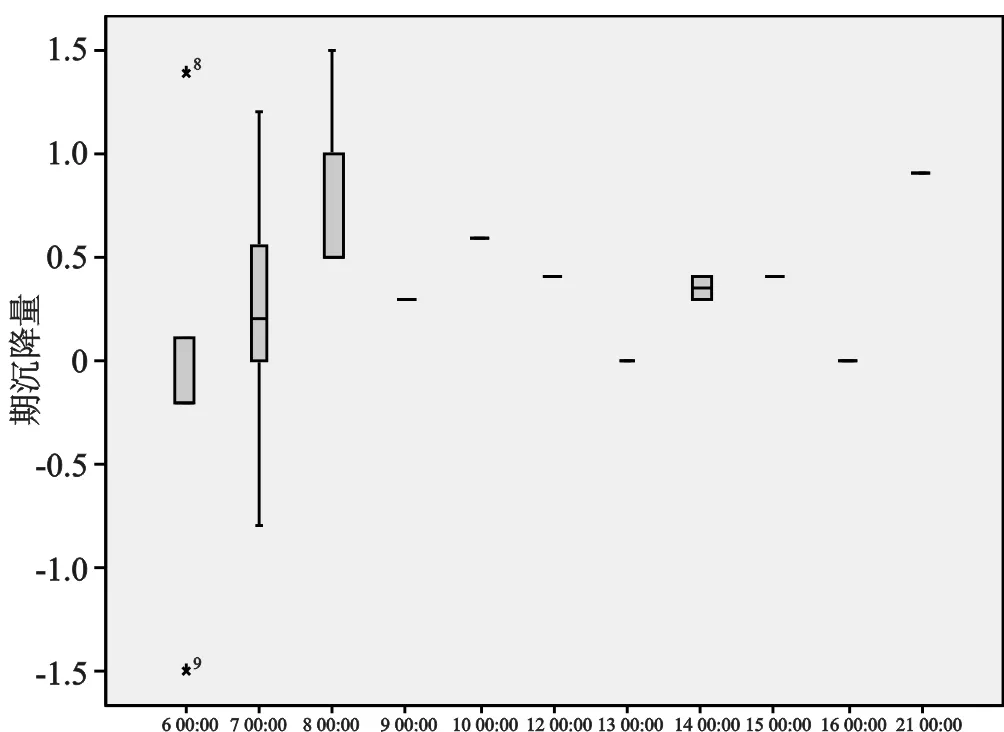
图7 箱图

由图7可知,在考虑时间间隔的情况下,第8期和第9期的数据存在异常。

通过两种探测思路的综合分析,得出第8期以及第9期的数据属于异常,需要在计算时进行排除。

2.2 数据异常值探测的检验

利用SPSS中的频数分析功能,通过比较去除异常值前后的计算结果,来对去除的效果进行检验,异常值消除前后频数分析如表4所示,直方图比较如图8所示。

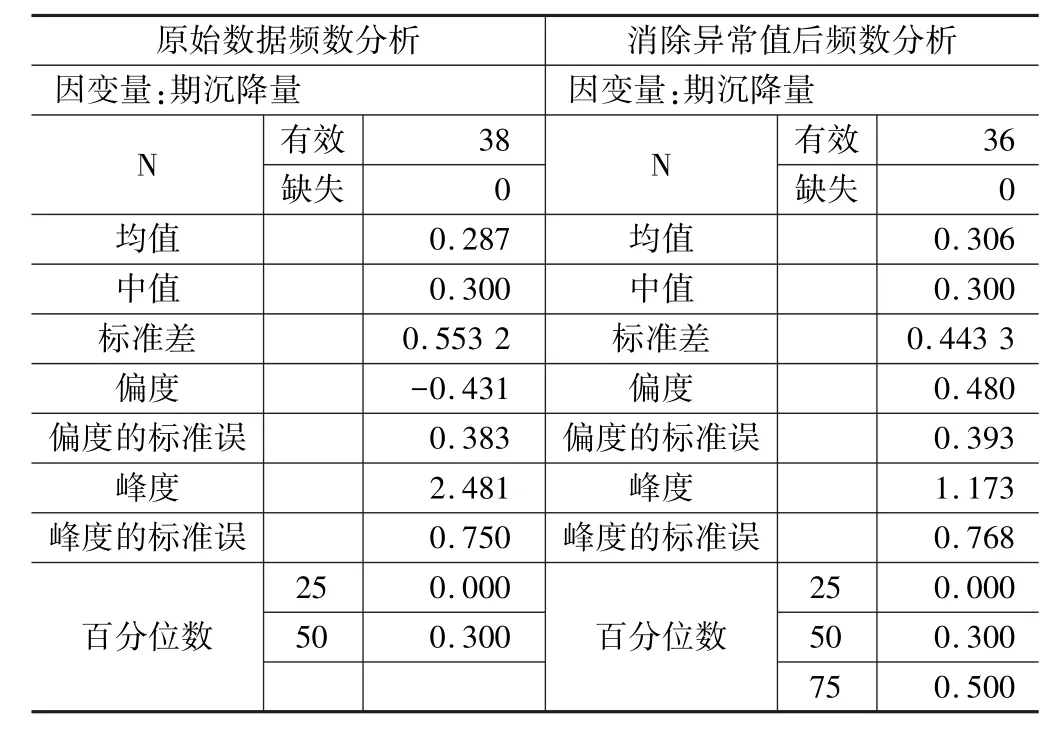
表4 异常值消除前后频数分析

图8 消除异常值前后直方图比较

从偏度和峰度来看,消除异常值后的数据确实能更好地表达沉降趋势。

3 沉降数据的回归分析

SPSS的曲线估计模块能够自动拟合包括线性模型、对数曲线模型、二次曲线模型和指数模型在内的十几种曲线模型。输出的统计量包括模型的回归系数、复向光系数、调整R方和方差分析表等。

由于沉降数据中存在非正数值,所以不能进行幂模型和指数模型计算。选取线性模型、二次曲线模型、对数模型,使用时间序列对该沉降点的累计沉降量进行回归分析,比较模型如表5、图9所示,数值比较如表6所示。

表5 模型与参数估计值输出(因变量:累计沉降量)

图9 三种模型曲线拟合图

表6 三种模型计算数据比较表(最后10期)

通过比较可以看出,线性模型达到的预测效果最好。

4 结 论

基于误差理论及精度控制,运用数理统计知识和SPSS软件,提出了对建筑物沉降观测数据进行异常值探测并进行科学取舍的思路和方法。经过样本测试,得到了回归分析法的曲线拟合法在预测沉降点变化中的各自的有效性和精确性。

本文研究的出发点仅是从单一变量对沉降量的影响进行考量,但是往往现场观测具有复杂性和沉降环境的多变性,因此对于不同的观测环境和地基条件,还待于获得更多资料进行更为详细的研究。

[1] 陈小荣,雷劲松.高层建筑沉降观测数据处理与分析新方法[J].四川建筑科学研究,2009(6):119～124.

[2] 游祖吉,樊功瑜.测量平差教程[M].北京:测绘出版社, 1991:279～281.

[3] 杜强贾丽燕.SPSS统计分析从入门到精通[M].北京:人民邮电出版社,2009.

[4] 陈东东,马大喜.某小区高层建筑沉降观测技术及数据分析[J].城市勘测,2013(5):127～130.

[5] 胡杰.形变分析中的模型精化研究[J].城市勘测,2012 (6):148～151.

Detection of Outliers and Regression Analysis Based on Observational Data SPSS for Settlement

Chen Wenhao
(Shantou Institute of Surveying and Mapping,Shantou 515041,China)

Settlement observation data affected by various factors,treatment is extremely important observation data, we propose the use of SPSS software for building settlement observation data to detect abnormal values and trade-offs of scientific ideas and methods,and after sample tests,analysis and comparison of the measured data several regression analysis predicting subsidence curve fitting point in changing their validity and accuracy.

SPSS;building;settlement;observations;outliers;probe;regression analysis

2014—02—02

陈文浩(1973—),男,工程师,现主要从事测绘技术与经营管理工作。