聚合物驱复合模型试井分析方法
2014-06-28郭辉程时清于海洋王成龙聂向荣张贤松冯国智
郭辉 ,程时清 ,于海洋 ,王成龙 ,聂向荣 ,张贤松 ,冯国智
(1.中国石油大学(北京)石油工程教育部重点实验室,北京 102249;2.中海油研究总院,北京 100027)
0 引言
试井分析是油藏动态监测较重要的手段[1-7],国内外许多学者对于双区复合油藏渗流特征及试井分析已有一定的研究,并已经出现了样板曲线。Ikoku等研究了非牛顿幂律流体的不稳定渗流特征[5-7],得出了考虑井筒储存和表皮效应均质无限大油层模型拉氏空间中的解。刘振宇等研究了非牛顿流体在多孔介质中的非稳态流动[8]。宋考平等研究了非牛顿-牛顿复合油藏渗流试井解释方法以及多区复合油藏非牛顿幂律流体试井解释[9-10]。刘彬等提出了适合稠油试井问题的牛顿-非牛顿复合油藏试井解释模型[11],这些为双区复合模型试井研究奠定了坚实的基础。
注聚合物驱时,通常采用聚合物和水交替注入的方式。聚合物驱替,聚合物流体视为非牛顿流体,聚合物没有驱替到的区域,流体渗流可视为牛顿型,从而形成非牛顿-牛顿复合模型。聚合物驱替后改为水驱,内区流体为牛顿型流体,外区的聚合物溶液为非牛顿流体,从而形成牛顿-非牛顿复合驱替。聚合物溶液在地层渗流时,不但存在剪切效应和黏弹效应,同时还存在其他的物理化学作用,提高了原油采收率[12]。
目前,国内外的试井典型曲线图版,绝大部分是把聚合物溶液流变特性简单地描述为幂律型流体,忽略了聚合物和地层岩石之间的作用,例如扩散、对流等作用[13-14]。 程时清和聂向荣等[15]在这方面作了深入研究,以聚合物流变实验为基础,考虑聚合物溶液在地层中存在扩散和对流作用的黏度模型,建立了聚合物驱试井解释数学模型,绘制了聚合物驱双区复合模型的试井典型曲线图版。
本文考虑剪切、扩散和对流等渗流因素,在文献[15]基础上,改进了聚合物的黏度模型,形成了更加准确的地层渗流黏度模型,并用实例说明了新模型的实际效用。
1 黏度模型
建立一个能够真实描述聚合物溶液在地层中的黏度模型,是试井参数准确解释的前提。幂定律仅能描述非牛顿区的流变行为,Meter式能够完整地描述整个流变曲线,是目前最常用的描述式之一,已经获得广泛的应用[16]。

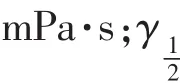
0剪切速率下聚合物溶液黏度为[17]
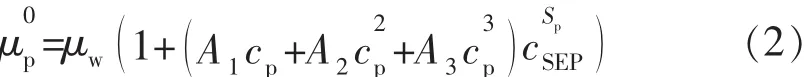
式中:cp为聚合物溶液质量浓度,g/L;cSEP为水相中有效阳离子浓度,g/L;Sp为实验资料确定的参数;A1为聚合物溶液参数,(g/L)-1;A2为聚合物溶液参数,(g/L)-2;A3为聚合物溶液参数,(g/L)-3。
由实验数据得出流变曲线,处理得到[18]
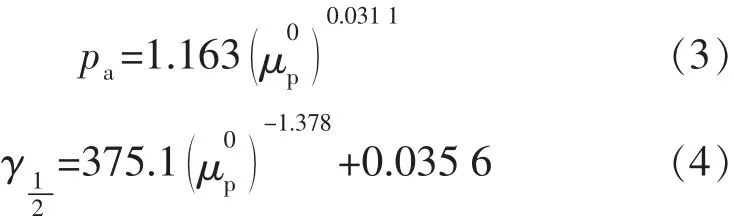
建立试井解释模型的时候,主要考虑的是渗流速度,因此需要建立剪切速度和渗流速度的关系[19-20]。

存在扩散、对流作用的聚合物溶液质量浓度为
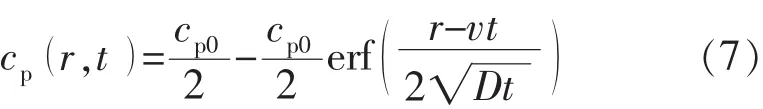
式中:C′为与迂曲度有关的系数;φ为孔隙度,%;K为渗透率,μm2;q 为流量,m3/d;h 为地层厚度,m;D 为扩散系数,cm2/s;t为时间,s;r为径向距离,m;cp0为聚合物溶液初始质量浓度,g/L;n为剪切速率指数;v为渗流速度,cm/s。
2 牛顿-非牛顿流体复合模型
2.1 数学模型
聚合物注入过程中,聚合物溶液驱替到的区域,渗流流体可认为非牛顿流体,而聚合物溶液驱替后又改为水驱的区域,渗流流体可认为牛顿流体;因此,聚合物驱段塞注入后再改为水驱油藏可用牛顿-非牛顿两区径向复合模型描述。假设条件为:内区流体为水相,外区为聚合物溶液,且均为微可压缩的流体;两区流体遵循达西渗流,渗流过程温度不变;考虑井储效应和表皮效应;两区渗流交界面不考虑附加压力降。基于上述条件,采用聚合物黏度模型,建立考虑表皮和井储效应影响的牛顿-非牛顿试井解释数学模型为
1)渗流方程内区:

外区:
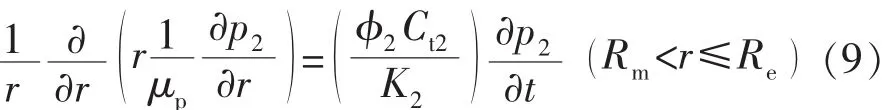
2)内边界条件
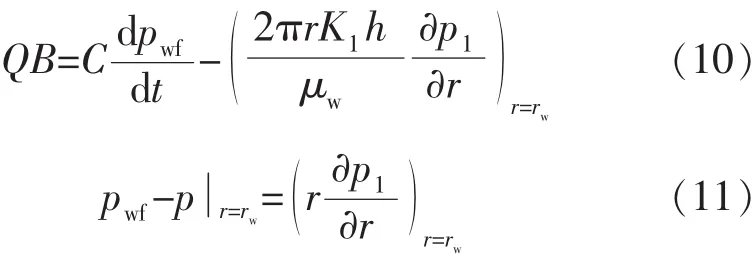
3)外边界条件

4)界面压力、流速相等条件
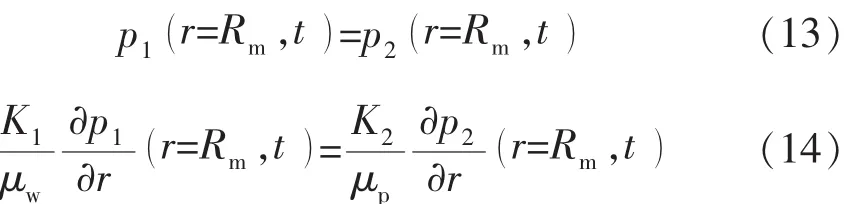
5)初始条件
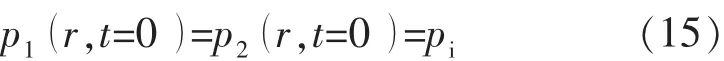
式中:p 为压力,MPa;pi为原始地层压力,MPa;pwf为井底压力,MPa;Ct为综合压缩系数,MPa-1;C 为井筒储集系数,m3/MPa;B为体积系数;S为表皮系数;Rm为内区半径,m;Re为供给边界半径,m; 下标:1表示内区,2表示外区。
2.2 模型求解及曲线特征
由于考虑了聚合物的非牛顿特性及扩散、对流等作用导致聚合物的质量浓度发生变化,建立的数学模型更加符合油藏实际情况,也更加复杂,导致利用现有的解析方法求解较困难,故而通过数值算法求解。通过对空间和时间进行网格划分,对渗流方程、边界条件和初始条件进行差分离散化,采用迭代求解方法求解差分方程组,得到井底的压力变化情况。
2.2.1 曲线流动段划分
聚合物溶液的特征参数:A1为 0.634 (g/L)-1,A2为0.193 (g/L)-2,A3为 0.921 (g/L)-3,cp0为 1.75 g/L,D 为0.024 6 cm2/s,μw为 0.5 mPa·s。 聚合物驱牛顿-非牛顿双区复合油藏试井模型试井典型曲线见图1。
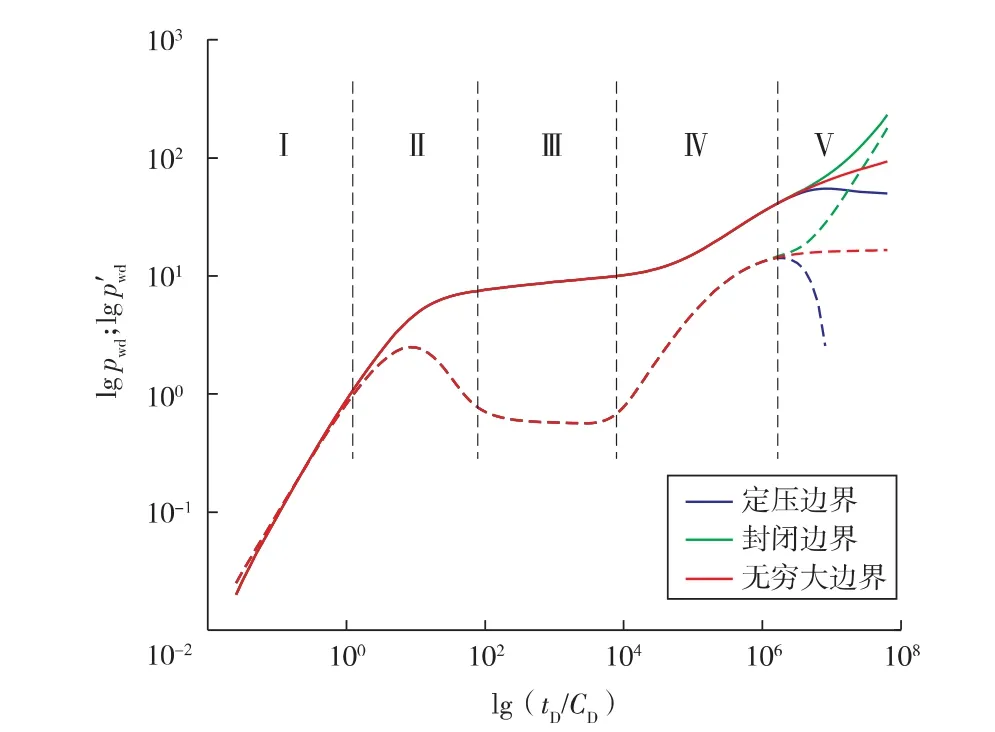
图1 牛顿-非牛顿双区复合模型典型
图1划分为5个流动段:第Ⅰ段为井储阶段,压力、压力导数曲线重合;第Ⅱ段为井储阶段到径向流的过渡阶段;第Ⅲ段是内区径向流段,压力导数曲线为0.5的水平直线段;第Ⅳ段是水相到聚合物溶液的过渡段;第Ⅴ段是内外区共同作用阶段,由于受到外区聚合物的影响,曲线表现出小幅度上翘。对于定压边界,压力曲线出现直线段,压力导数曲线上出现迅速下掉。封闭边界,压力曲线和压力导数曲线出现迅速上翘。
2.2.2 曲线特征
聚合物溶液质量浓度影响见图2。内区水相黏度一定,外区聚合物初始质量浓度越大,聚合物黏度也就越大,导致内区到外区流动阻力增大,水相到聚合物溶液的过渡段上翘幅度越大;外区聚合物溶液的非牛顿特性则导致了两区共同作用段出现小幅度上翘。
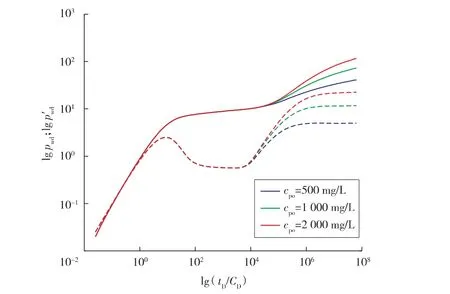
图2 聚合物初始质量浓度的影响
内区半径Rm的影响见图3。Rm越大,水相径向流段时间越长,水相到聚合物的过渡段出现得越慢。

图3 内区半径的影响
3 非牛顿-牛顿流体复合模型
3.1 数学模型
聚合物注入过程中,以注聚合物井为中心,聚合物溶液驱替到内区过程中,渗流流体可认为非牛顿流体,而聚合物溶液没有驱替到的外区,渗流流体可认为牛顿流体,因此聚合物驱油藏可用非牛顿-牛顿复合模型描述,内区为聚合物流体,外区为油相流体。与牛顿-非牛顿模型边界条件、初始条件相同,渗流方程为
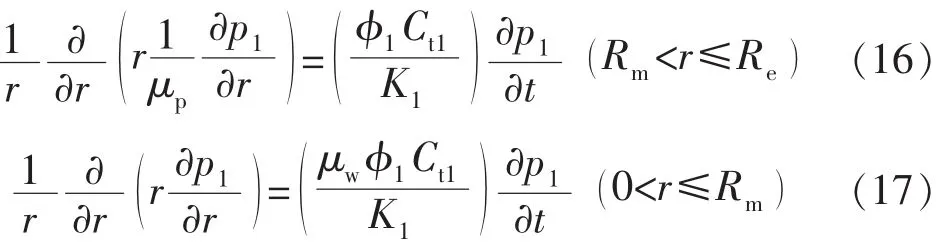
3.2 曲线特征
3.2.1 曲线流动段划分
聚合物驱非牛顿-牛顿双区复合油藏试井典型曲线见图4。曲线同样划分为5个流动段,与图1的区别在于第Ⅲ阶段的内区径向流段,由于内区为聚合物溶液,径向流段压力导数曲线呈现一定斜率。
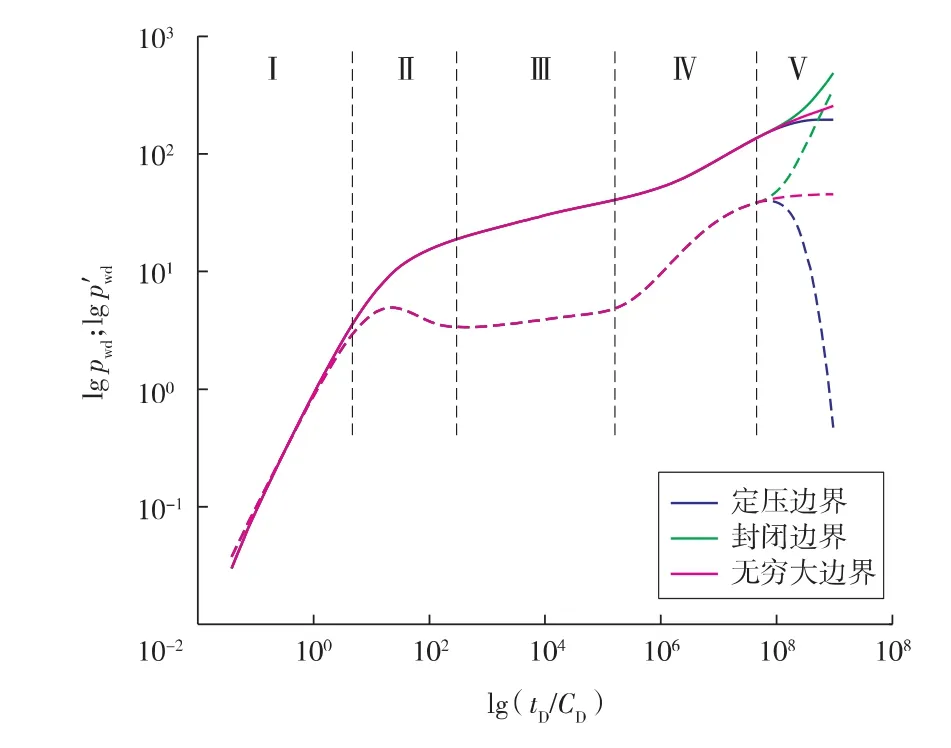
图4 非牛顿-牛顿双区复合油藏典型曲线
3.2.2 曲线敏感性分析
聚合物溶液质量浓度的影响见图5。聚合物溶液初始质量浓度越大,内区流体的黏度也大,在内区径向流段上翘的幅度也越大;随着聚合物质量浓度增加,内外区过渡段上翘幅度减小,这是由于外区油相黏度一定,内区聚合物的黏度越大,内外区流动系数差异越小,导致内外区过渡段斜率减小。
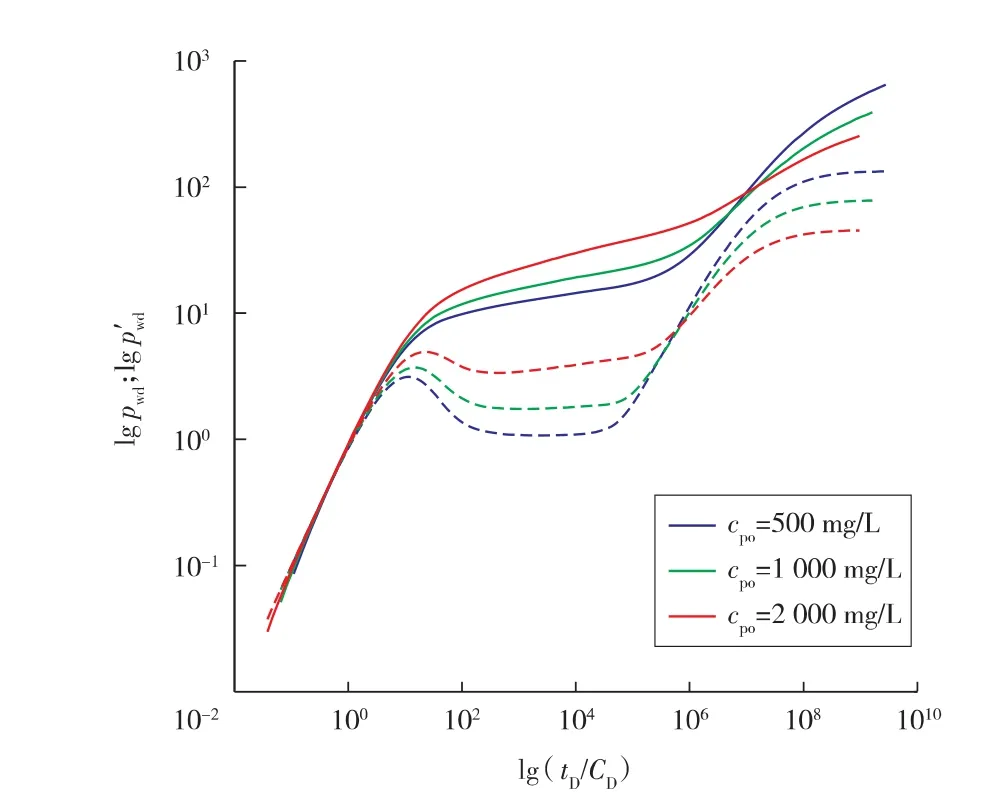
图5 聚合物初始质量浓度的影响
图6为外区油相黏度的影响。外区油相黏度较小时,两区流度比较小,压力导数曲线会出现下掉,油相黏度较大时,两区流度比较大,油相黏度越大,聚合物溶液到油相的过渡段上翘幅度越大。
4 实例应用
聚合物驱试井复合模型应用于实际资料解释,其解释步骤:1)根据注入井流体驱替特征,选择复合模型。如先注入聚合物,再注水,选择牛顿-非牛顿复合模型,反之,选择非牛顿-牛顿复合模型。2)绘制实测压力数据双对数图,与样板曲线进行拟合,计算地层平均压力、内区渗透率、表皮系数、井储系数、外区渗透率、内区半径等参数。
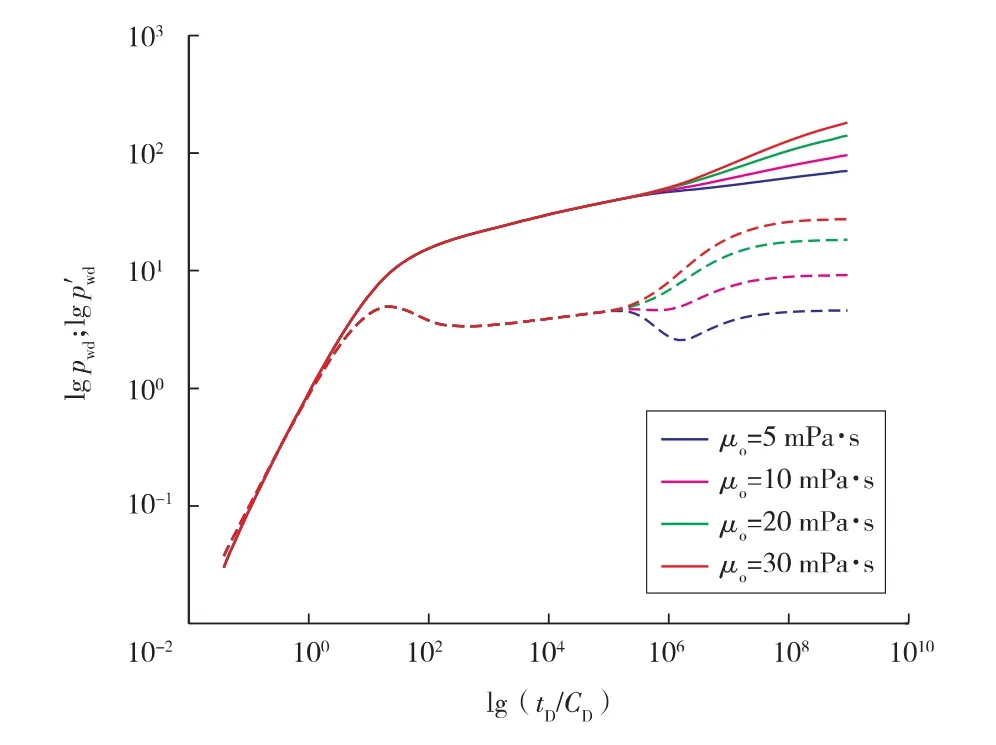
图6 外区原油黏度的影响
油田某注聚井,试井数据为:井径0.1 m,注聚量100 m3/d,油层厚度10 m,油相体积系数1.1,孔隙度30%,原油黏度 14.3 mPa·s,水相黏度 0.5 mPa·s,综合压缩系数0.001 4。
实测数据与理论典型曲线拟合情况见图7,曲线拟合良好。解释结果为:水和聚合物交界面距离注聚井65.51 m,地层平均压力18.75 MPa,内区渗透率1.79 μm2,表皮系数 2.18,井筒储集系数1.82 m3/Pa,外区渗透率1.28 μm2。该结果符合油田实际情况。
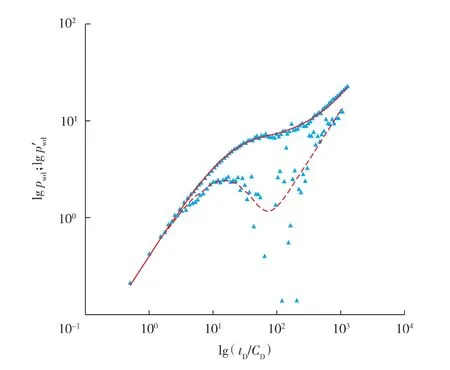
图7 实测数据与典型曲线的拟合
5 结束语
采用新的聚合物驱试井黏度模型,建立了考虑剪切、扩散、对流的聚合物和水交替驱替的2种双区复合试井数学模型,通过数值求解,绘制出复合模型典型曲线,复合模型试井解释方法可解释两区油藏参数。实例验证,该方法较好地描述了聚合物驱替动态特征。
[1]廖新维,沈平平.现代试井分析[M].北京:石油工业出版社,2002:150-155.
[2]于九政,晏耿成,巨亚锋,等.低渗油藏注水井试井压力响应机理及解释模型[J].断块油气田,2013,20(1):92-95.
[3]李顺初,黄炳光,李晓平,等.复合油藏压力分布研究[J].断块油气田,2001,8(6):29-32.
[4]张艳玉,何艳萍.均质地层变井储试井分析[J].断块油气田,1997,4(4):34-38.
[5]Ikoku C U,Ramey H J Jr.Transient flow of non-Newtonian power-law fluids in porous media[J].SPEJ,1979,19(6):164-174.
[6]Lund O,Ikoku C U.Pressure transient behavior of non-Newtonian/Newtonian fluid composite reservoirs [J].SPEJ,1981,21 (4):271-280.
[7]Ikoku C U,Ramey H J Jr.Wellbore storage and skin effects during the transient flow of non-Newtonian power-law fluids in porous media[J].SPEJ,1980,20(1):137-225.
[8]刘振宇,翟云芳,卓兴家,等.非牛顿流体在多孔介质中的非稳态流动[J].大庆石油学院学报,1995,19(4):18-21.
[9]宋考平,王雷,计秉玉.非牛顿-牛顿复合油藏渗流试井解释方法[J].石油学报,1996,17(1):82-86.
[10]宋考平,祝俊峰,刘泽俊.多区复合油藏非牛顿幂律流体试井解释[J].石油学报,1997,18(2):78-83.
[11]刘彬,贾永禄,霍进,等.稠油热采牛顿/非牛顿渗流复合油藏试井解释模型[J].油气井测试,2006,15(3):1-4.
[12]张波,由庆,张健,等.海上油田聚合物驱降压增注技术[J].断块油气田,2010,17(5):624-627.
[13]徐建平,王连泽,张宝海.双渗透聚合物驱油藏不稳定压力动态[J].清华大学学报:自然科学版,2004,44(2):236-239.
[14]刘泽俊,孙智,宋考平.有界地层非牛顿渗流试井解释模型[J].大庆石油地质与开发,1996,15(3):63-64.
[15]程时清,聂向荣.聚合物驱复合油藏试井模型与典型曲线[J].华中科技大学学报:自然科学版,2012,40(4):110-113.
[16]Delshad M.UTCHEM version 6.1 technical documentation[R].Austin:Center for Petroleum and Geosystems Engineering,1997:124-126.
[17]陈国,赵刚,马远乐.黏弹性聚合物驱油的数学模型[J].清华大学学报:自然科学版,2006,46(6):883-885.
[18]方道斌,郭睿威,周少刚.水解聚丙烯酰胺盐水溶液表观黏度的数学模拟[J].化工学报,1997,48(1):80-84.
[19]王新海.聚合物数值模拟主要参数的确定[J].石油勘探与开发,1990,15(3):69-76.
[20]王健.化学驱物理化学渗流理论与应用[M].北京:石油工业出版社,2008:62-65.
