通过“几何画板”使抽象思维形象化与动态化

季卫新

(南京师范大学附属中学江宁分校 江苏 南京 211102)

“从生动的直观到抽象的思维”是人类认识发展的基本规律.正确地运用直观性学习原则，可以激发学生的学习兴趣和热情，引起对教学内容的选择性知觉，从而有助于对所学知识的领会、理解和掌握,提高学习的质量.因此，抽象思维“形象化”是当前应着手解决的问题，而解决的办法之一，就是用“画”来完成对抽象思维的描述和诠释，通过“几何画板”使抽象思维形象化、动态化，可以帮助学生分析和理解问题.

1 一条光学竞赛题

【例1】(2009年上海市第二十三届初中物理竞赛初赛试题第26题)如图1(a)所示，平面镜OM与ON夹角为θ，光线AB经过平面镜的两次反射后出射光线为CD．现将平面镜OM与ON同时绕垂直纸面过O点的轴转过一个较小的角度β，而入射光线不变，如图1(b)所示．此时经过平面镜两次反射后的出射光线将

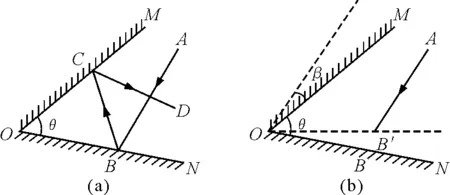
图1

A．与原先的出射光线CD平行

B．与原先的出射光线CD重合

C．与原先的出射光线CD之间的夹角为2β

D．与原先的出射光线CD之间的夹角为β

1.1 抽象思维解题模式

因为保持平面镜OM与ON夹角θ不变，将平面镜OM与ON同时绕垂直纸面过O点的轴转过一个较小的角度β，则入射角增大或减小β，反射角也增大或减小β，所以反射光线与入射光线的夹角是2β，即反射光线偏转2β角.

又因为平面镜OM与ON同时绕垂直纸面过O点的轴转过一个较小的角度β时，两平面镜OM与ON仍互成θ角，角度没变，所以第二次的反射光线方向不变；又因为入射光线不变，所以此时经过平面镜两次反射后的出射光线将与原先的出射光线CD重合．故选项B正确．

1.2 抽象思维解题模式的点评

该题是一道典型的“抽象思维”题，对于初中学生来说，没有图1(b)的辅助，几乎无法思考.该题抽象之处在于，虽然有两个“不变量”——入射光线AB方向不变和平面镜OM与ON夹角θ不变.但是，当平面镜OM与ON同时绕垂直纸面过O点的轴转过一个较小的角度β时，入射光线AB在平面镜ON表面进行反射的反射光线B′C′的方向要发生改变；同时，由于平面镜OM的位置(或者称之为角度)也会发生改变，导致在转动过程中出现了3个“变化量”，那么最后的二次反射光线C′D′是否会发生改变呢？如果变，怎么变呢？

所以，即使有了图1(b)的辅助，但是由于学生“抽象思维”能力的缺陷，仍然无法在头脑中展现完整的“转动过程”的“思维图像”，因此在思维过程中仍然是“抽象”的，无法理清楚3个“变量”导致的结果是什么.

把这3个“变量”再次明确一下，一是平面镜ON的位置；二是入射光线AB在平面镜ON表面进行反射的反射光线B′C′的方向；三是平面镜OM的位置.

1.3 利用“几何画板”形象“画”来分析

本文使用的是《几何画板》5.06最强中文版，该软件可以很容易在网络上下载，不再多介绍.关于该软件的基本操作和术语，也请自行学习和参考软件附带的《使用手册》.

1.3.1 “画”的方法和步骤

(1)点击“角工具”， 选择“作45°角”，作出一个固定角度的“角”，并且把两条边分别标注为“OM”和“ON”，将角度标注为θ，这就是“夹角为θ的平面镜OM与ON”.

(2)点击“直线工具”，画出一条只与平面镜ON相交的直线，该直线与ON的交点标注为“B”，则该直线就是“入射光线AB”.

(3)选择“直线ON”和“点B”，点击“构造菜单”，选择“垂线”，并且将该直线改为“虚线”，则该直线就是过B点ON的“法线”.

(4)选择“ON的法线”，点击“变换菜单”，选择“标记镜面”；然后选择“入射光线AB”，点击“变换菜单”，选择“反射”，即可得到AB的反射光线，该直线与直线OM有一个交点，请标注为“C”，则直线BC就是第一次的反射光线.

(5)选择“直线OM”和“点C”，点击“构造菜单”，选择“法线”，并且将该直线改为“虚线”，则该直线就是过C点OM的“法线”.

(6)选择“OM的法线”，点击“变换菜单”，选择“标记镜面”；然后选择“入射光线BC”，点击“变换菜单”，选择“反射”，即可得到BC的反射光线，则该直线就是第二次的反射光线.

到此，“画”的步骤结束，请将文件保存.最终效果图如图2所示.

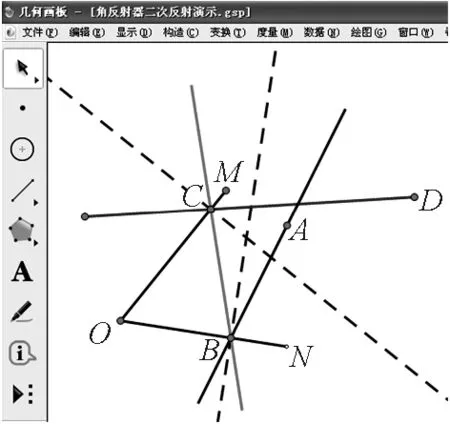
图2 最终效果图

1.3.2 “思考”的注意点和过程

将鼠标点击“移动箭头工具”，选择“点N”，鼠标左键按住不放，上下拖动，使得“∠MON”绕点“O”转动，即相当于“将平面镜OM与ON同时绕垂直纸面过O点的轴转过一个较小的角度β”.很明显可以直观地观察到“直线CD方向不变”，从而得到答案为选项B.与原先的出射光线CD重合．

(1)为了便于观察和比较“直线CD方向是否不变”，可以单独“画”一条直线，使其与“直线CD重合”.因为单独“画”的那条直线位置和方向都不会发生改变，可以作为比较的参照物.

(2)为了使画面简洁、明了，可以将两条“法线”设置为“隐藏”，或者将 “颜色”设置为浅色.

(3)为了使结论更具有普遍性，应该将点“N”向上和向下都拖动.

(4)也可以设置一个函数，用以改变“∠MON”的度数，增加结论的普遍性,甚至调整到90°，来演示“角反射器”的效果.

2 一道力学中考题

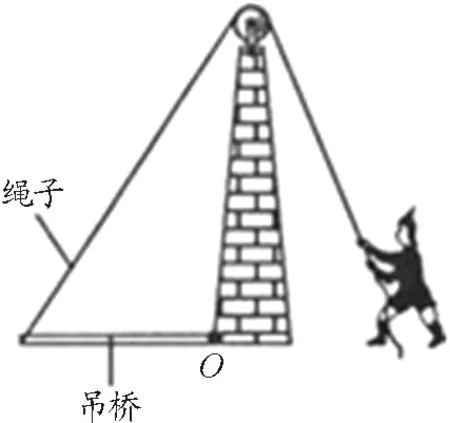
图3

【例2】(2005年北京市海淀区中考试题)古代护城河上安装的吊桥可以看成一个以O为支点的杠杆，如图3所示.一个人通过定滑轮用力将吊桥由图示位置缓慢拉至竖直位置.若用L表示绳对桥板的拉力F的力臂，则关于此过程中L的变化以及乘积FL的变化情况，下列说法正确的是

A．L始终在增加，FL始终在增加

B．L始终在增加，FL始终在减小

C．L先增加后减小，FL始终在减小

D．L先减小后增加，FL先减小后增加

2.1 抽象思维解题模式

当吊桥被吊起的过程中，如图4中虚线位置1所示，吊桥重力的力臂L′在减小，而吊绳的拉力的力臂L却在增大，根据杠杆的平衡条件FL=GL′可知，FL在减小；当吊桥被吊到虚线位置2的过程中，重力的力臂L′继续减小，所以FL仍在减小，而F的力臂L则由大变小．故选项C正确．

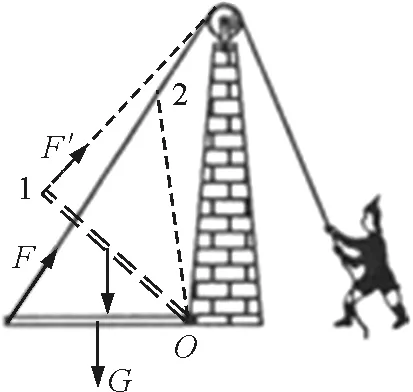
图4 最终效果图

2.2 抽象思维解题模式的点评

与所有的抽象题型一样，本题也是一个动态变化题.当吊桥被吊起的过程中，只有一个不变量——吊桥的重力G.在动态变化过程中，存在3个变量，一是吊桥重力的力臂L′；二是吊绳拉力的力臂L；三是吊绳的拉力F.

根据杠杆的平衡条件FL=GL′可知，该过程共存在4个量.一般情况下，利用杠杆的平衡条件进行定性分析时，需要确定两个量“不变”，那么第4个量随第3个“变量”而“变”的关系就可以判断了.如果存在3个同时改变的“变量”，则问题就复杂多变，而且“抽象”了.

同样，虽然可以通过“画”分析图来帮助理解和思考，但是由于 “画”在纸上的图片是“静态”的，无法做到“同步动态”展现，所以导致思维过程仍然具有很大的“抽象性”.

2.3 利用“几何画板”形象“画”来分析

同例1一样，下面先介绍“动画”的制作过程.为了使效果更具有适用性，下面的过程将涉及到一些“函数”的使用和较复杂的构造.

2.3.1 “画”的方法和步骤

(1)点击“线段工具”，在画板上画出一条线段，该线段代表地面.

(2)点击“点工具”，在“地面”上随意确定一个点；点击“线段工具”，过刚才的点画出一条垂直“地面”的线段，长度适中，该线段代表“城墙”.

(3)点击“数据菜单”，选择“新建函数”；将“名称”命名为“吊桥长度”；“初始值”为“4”；“单位”选择“距离”.

(4)点击“点工具”，在“城墙”线段下方确定一个点“O”，作为“吊桥”的支点.

(5)选择点“O”和函数“吊桥长度”，点击“构造菜单”，选择“以圆心和半径绘圆”，可以得到一个圆O，其半径可以随函数“吊桥长度”数值的改变而改变；其位置可以随点“O”的改变而改变.

(6)点击“点工具”，在圆O右侧弧上确定一个点“D”；选择点“O”和点“D”，点击“构造菜单”，选择“线段”，这样可以得到线段OD，则代表“吊桥”.

(7)点击“圆工具”，以“城墙”上端的端点为圆心，画出一个很小的圆，作为“城墙上的定滑轮”.

(8)点击“点工具”，在“定滑轮”上部确定一个点“K”，选择点“K”和点“D”，点击“构造菜单”，选择“线段”，这样可以得到线段“KD”，则代表“吊绳”.

(9)选择点“O”和线段“KD”，点击“构造菜单”，选择“垂线”，该垂线与线段“KD”的交点标注为“A”；选择点“O”和点“A”，点击“构造菜单”，选择“线段”，这样可以得到线段“OA”，则代表“动力臂L”；隐藏刚才的“垂线”，并且把线段“OA”设置为“虚线”.

(10)点击“点工具”，在圆O右侧弧上确定一个点“E”，使直线“OE”与“城墙”夹角为90°；将点“D”移动到与点“E”重合，此时直线“KD”与圆O有一个交点；点击“点工具”，在圆O右侧弧上该位置确定一个点“N”.

(11)先后选择点“D”和点“N”，点击“编辑菜单”，点击“操作类按钮”，选择“移动”，则出现如图5所示窗口.将“标签”命名为“向上拉动”，其余设置如图5所示.

图5 操作类按钮

(12)先后选择点“D”和点“E”，点击“编辑菜单”，点击“操作类按钮”，选择“移动”.将“标签”命名为“复位”，其余设置同上.

(13)点击“点工具”，在线段“OD”大约中点位置上确定一个点“B”；选择点“B”和“地面”，点击“构造菜单”，选择“垂线”，得到的直线代表“竖直方向”(就是重力方向)；点击“线段工具”，过点“B”画出一条合适长度的线段，代表“吊桥的重力”.

到此，制作大功告成，可以将一些辅助线条和元素隐藏，使画板较为清晰.最终效果如图6(a)所示.

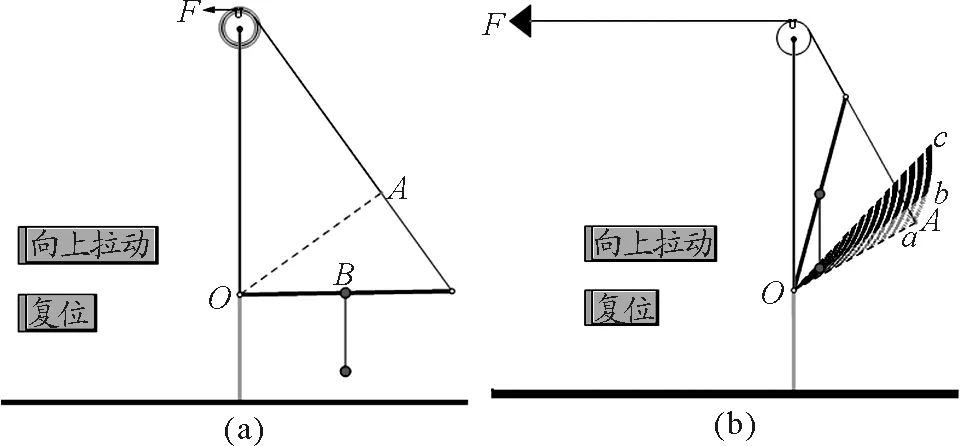
图6 吊桥长度较小

2.3.2 “思考”的注意点和过程

为了能直观、显现地动态显示“力臂”的变化，可以使用“几何画板”的“追踪功能”.例如，本文采用了“追踪点”的功能.

方法很简单,选择需要“追踪”的对象，点击“显示菜单”，选择“追踪……”即可；也可以在选择需要“追踪”的对象后，右击鼠标，在弹出的窗口直接选择需要的“追踪对象”.本题中，最好同时追踪“动力臂L”和“阻力臂L′”.

另外，本题需要分以下两种情况进行分析：

(1)如图6(a)所示，如果吊桥长度比城墙高度小得较多.通过软件的运行和动态过程轨迹显示，如图6(b)所示，动力臂OA的末端运动轨迹为b-c-b-a.非常直观地显示出动力臂的变化情况是,先由小变大，再由大变小；而且，在整个过程中，动力臂却是始终大于阻力臂的.

(2)如果吊桥长度比城墙高度大的话，设计界面如图7(a)所示.通过软件的运行和动态过程轨迹显示，如图7(b)所示.动力臂OA的末端运动轨迹是单一方向的.非常直观地显示出动力臂的变化情况是一直变大.

由上可以看出，借助“几何画板”巧妙“用图”不但能解决难题，而且还有发散性探究乐趣，对于抽象的物理问题的分析是非常有益的.

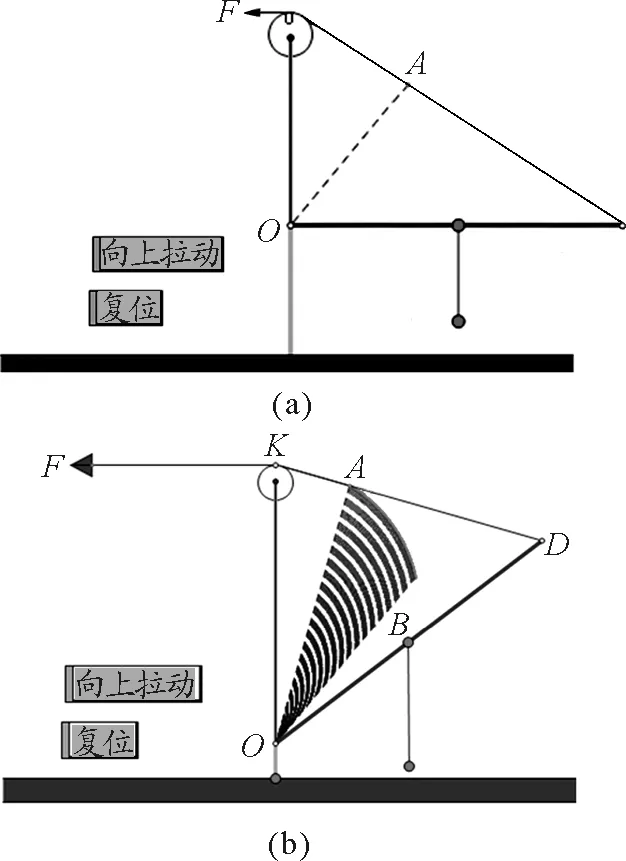
图7 吊桥长度较大

3 结束语

“几何画板”是“直观几何计划”的一部分，它具有丰富的图形绘制功能、 “动态性”、独特的“度量”和“计算”功能、操作方便简单等特点.

强大的图形和描绘轨迹等动画功能动态地保持了几何图形中内在的、恒定不变的几何关系及规律，可从中观察事物的现象，通过类比和分析提出问题、解决问题，从而发现恒定不变的几何规律，化抽象为形象，化静态为动态，能寓趣味性、技巧性和知识性于一体.

使用几何画板制作课件，体现的不是编程水平，而是教师的教学思想和教学水平以及几何构建思想.许多物理难题，由于其题设情境一般都是动态的，变化性强，需要学生拥有很强的“抽象思维能力”.借助“几何画板”，利用软件特点，可以很容易做到将“抽象思维”进行“形象‘画’”，从而使思维变得形象、动态，降低问题的难度，让学生可以更多地获取成功的体验，增强对物理学科的兴趣.

参考文献

1 朱铁成. 形象思维和抽象思维的本质及其对物理教学的启示. 浙江师范大学学报(自然科学版),2001(01)

2 朱铁成,陈报南. 物理学习形象思维和抽象思维的特点探讨. 广西物理,2000(04)

3 潘丽珍. 中学物理教学中形象思维能力培养初探:[学位论文]. 福州：福建师范大学，2013