如何求解不同类型动态变化电路问题
2014-06-28董淑华
董淑华
(甘肃省肃北中学 甘肃 酒泉 736300)
动态变化电路问题是初中物理教学的重、难点,同时也是中考物理的必考点,由于涉及的知识点较多,几乎覆盖了电学中所有重要的规律,综合性较强,许多学生遇到后往往找不到问题的突破口而束手无策.下面笔者就借助典型例题来谈谈此类问题的解决方法.
1 开关的通断引起的动态变化电路问题
【例1】如图1所示,电源电压不变,开关由断开变为闭合后,下列说法正确的是
A.电流表示数增大
B.电流表示数减小
C.电压表示数增大
D.电压表示数减小
解析:无论开关断开还是闭合,电压表均测的是电源电压,故示数不发生改变.当开关S闭合后,构成R1与R2的并联电路,总电阻小于R1,电流表示数增大.
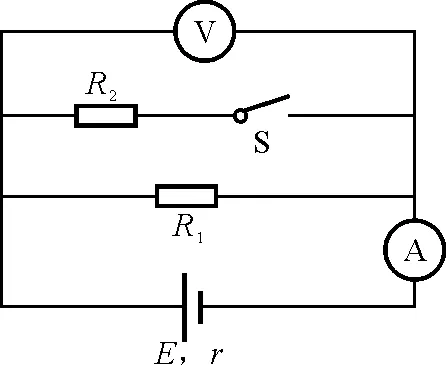
图1
答案:A.
【例2】某电热水器的工作原理如图2所示(已知两电阻丝的阻值相等,电源电压保持不变),它有加热和保温两个工作状态,当开关S1接b,S2断开时,它处于______状态,此时电路功率为P1;开关S1接a,S2闭合时,它处于______状态,此时电功率为P2,则P1∶P2=______.
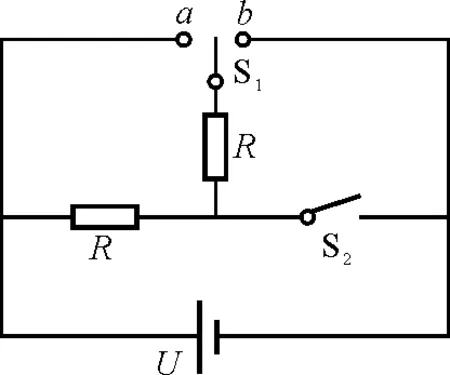
图2
解析:当开关S1接b, S2断开时,两电阻丝串联,根据焦耳定律Q=I2Rt得此时处于保温状态,可得
(1)
当开关S1接a,S2闭合时,两电阻丝并联,总电阻减小,电流增大,根据焦耳定律Q=I2Rt,此时处于加热状态,可得
(2)
联立式(1)、(2)得
答案:保温状态;加热状态;1∶4.
此类题目的特点是,由于开关的通、断引起电路的连接方式改变,使电路中总电阻改变而引起电流发生改变.解决此类问题的关键是搞清楚开关的断、通使电路的连接方式如何变化,电阻和电流随电路的连接方式如何变化,从而找到解决问题的突破口.
2 滑动变阻器滑片移动引起的动态变化电路问题
【例3】如图3所示的电路中,滑动变阻器的滑片P向右移动时,电流表的示数______,电压表的示数______.
解析:将电压表断路,判断电路为串联电路,电压表接在滑动变阻器滑片P上,滑片移动不能改变电路中的总电阻,电路中的总电阻不变,故总电流不变,电流表示数不变;但电压表测的是与之并联部分电阻的电压,故电压表示数变大.
答案:不变;变大.
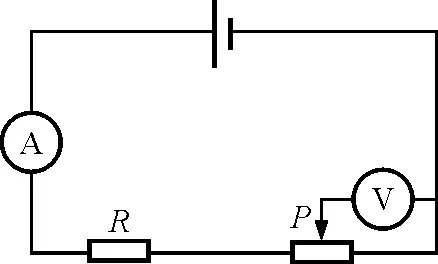
图3
解决此类问题的关键是判断电路连接方式,根据电路连接方式,先判断滑动变阻器引起的总电阻变化,随后判断电流表示数的变化,排除错误答案,再判断电压表如何变,进而得出结论.
3 由开关通断和变阻器滑片移动共同引起的动态变化电路问题
【例4】如图4所示,电源电压为6 V保持不变,电阻R1=10 Ω,变阻器R2的最大阻值为60 Ω,灯L标有“6 V,0.72 W”字样,问:
(1) 当R2的滑片移至最左端时,要使L正常发光,开关S1和S2应处于什么状态?
(2)S1, S2都断开时,灯L在5 min内消耗的电能是多少?
(3)闭合S1,S2,调节滑动变阻器的滑片,电流表的示数最小时,整个电路的电功率是多少?
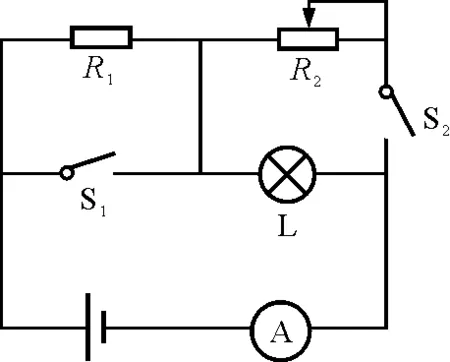
图4
解析:(1)此时若S1,S2都断开,则灯L不能正常发光;若闭合S2,则灯L被短路;当闭合S1,断开S2时,电阻R1被短路,灯L两端的电压为6 V,属于正常发光.同时还可以求得L的电阻为
代入数据得
RL=50 Ω
(2)当开关S1,S2都断开时,只有R1与L串联在电路中,电路中的电流为
代入数据得
I=0.1 A
则灯L在5 min内消耗电能为
W=I2RLt
代入数据得
W=150 J
(3)闭合开关S1,S2时,R2与L并联,R1被短路,这时只有当滑动变阻器的滑片移至最右端时,即R2=60 Ω时,电路中的电流最小,此时整个电路的等效电阻为
代入数据得
整个电路消耗的电功率为
代入数据得
P=1.32 W
4 电流表及电压表连接方式改变引起的动态变化电路问题
【例5】如图5所示的电路中,电源电压保持不变,电阻R2与R3的阻值为30 Ω,闭合开关S,电流表○A1和○A2的示数之比为2∶1,若把电流表○A1换成电压表○V1,电流表○A2换成电压表○V2后,电压表○V1的示数为U1, 电压表○V2的示数为U2,则
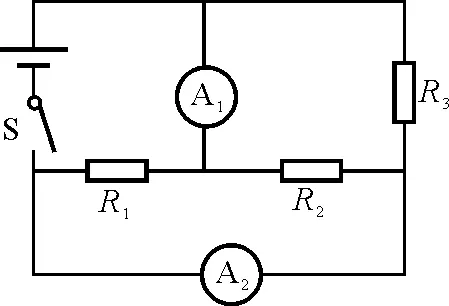
图5
A.R1=15 Ω
B.R1=30 Ω
C.U1∶U2=3∶2
D.U1∶U2=2∶1
解析:当接电流表○A1与○A2时,由电路图分析可知R1,R2,R3构成并联电路,○A1测量的是通过R1与R2的总电流IA1,○A2测量的是通过R2与R3的总电流IA2,则
(3)
(4)
由题意知
IA1∶IA1=2∶1
(5)
联立式(3)~(5)得
R1=10 Ω
当把电流表○A1换成电压表○V1,电流表○A2换成电压表○V2时,电路变为R1,R2,R3的串联电路,电压表○V1测R2,R3两端电压,电压表○V2测R1,R2两端电压,由串联电路电压与电阻的关系得
代入数据得
答案:C.
由于动态电路的开关通、断,变阻器滑片的移动或电流表、电压表位置改变,电路的连接以及电路中某些物理量也随之改变,使得电路计算变得复杂.解答此类问题,应抓好3个环节:
一是题图对照,侧重识图;
二是梳理条件,抓住关键,找出突破口
三是明确解题思路,综合运用公式进行计算.
注意两个要点:一是严格区分不同条件下的电路,分别列出相关的关系式;二是结合题目的已知条件,寻找解题的突破口并进行计算.
